福建省福州市平潭县新世纪学校2020-2021学年高一下学期5月数学补习练(10)试题 Word版含答案
文档属性
| 名称 | 福建省福州市平潭县新世纪学校2020-2021学年高一下学期5月数学补习练(10)试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 990.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 00:00:00 | ||
图片预览




文档简介
平潭县新世纪学校2020-2021学年高一下学期数学补习练(10)
一、单选题
1.平面false与平面false平行的条件可以是( )
A.false内有无穷多条直线与false平行 B.false内的任何直线都与false平行
C.直线false在平面false内,直线false在平面false内,且false,falseD.直线false,直线false
51816001219202.下列命题中,错误的是( )
A.平行于同一直线的两个平面互相平行 B.平行于同一平面的两个平面互相平行
C.若一条直线与两个平行平面中的一个相交,则这条直线与另一个平面也相交
D.夹在两平行平面间的平行线段相等
56388002057403.如图,在四棱锥false中,底面false是平行四边形,点false,false分别是false,false的中点,点false在线段false上,且false,则( )
A.false B.直线false与直线false相交 C.false D.false平面false
4.若false是两个不同的平面,l,m,n是三条不同的直线,则false成立的充分不必要条件是
5667375150495A.false B.false C.falseD.false
5.在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为( )A.90° B.45° C.60° D.30°
5505450171456.如图所示,将无盖正方体纸盒展开,直线AB、CD在原正方体中的位置关系是( )
A.平行 B.相交且垂直 C.异面直线 D.相交成60°角
7.如图,已知三棱柱false的各条棱长都相等,且false底面false,false是侧棱false的中点,则异面直线false和false所成的角为( )
4819650304800A.false B. C. D.false
8.如图1,直线false将矩形false分为两个直角梯形false和false,将梯形false沿边false翻折,如图2,在翻折过程中(平面false和平面false不重合),下列说法正确的是( )
A.在翻折过程中,恒有直线false平面false B.存在某一位置,使得false平面false
C.存在某一位置,使得false D.存在某一位置,使得false平面false
二、填空题
9.如图,在边长为2的正方体false中,点P是该正方体对角线false上的动点,给出下列四个结论:
468630069215①false②false面积的最大值是false
③false面积的最小值是false④当false时,平面false平面false
其中所有正确结论的序号是___________.
53911503619510.已知false,false是平面false外的两条不同直线,给出下列三个论断:①false;②false;③false.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:
522922566484511.如图,在四面体false中,false,false与false所成的角为false,false、false分别为false、false的中点,则线段false的长为________.
12.如图所示,正方体false的棱长为false,false为false的中点,false点是正方形false内的动点,若false平面false,则false点的轨迹长度为______.
三、解答题
13.如图,在四棱锥false中,底面false是矩形.
(1)设false为false上靠近false的三等分点,false为false上靠近false的三等分点.求证:false平面false.
(2)设false是false上靠近点false的一个三等分点,试问:在false上是否存在一点false,使false平面false成立?若存在,请予以证明;若不存在,说明理由.
3390900653415
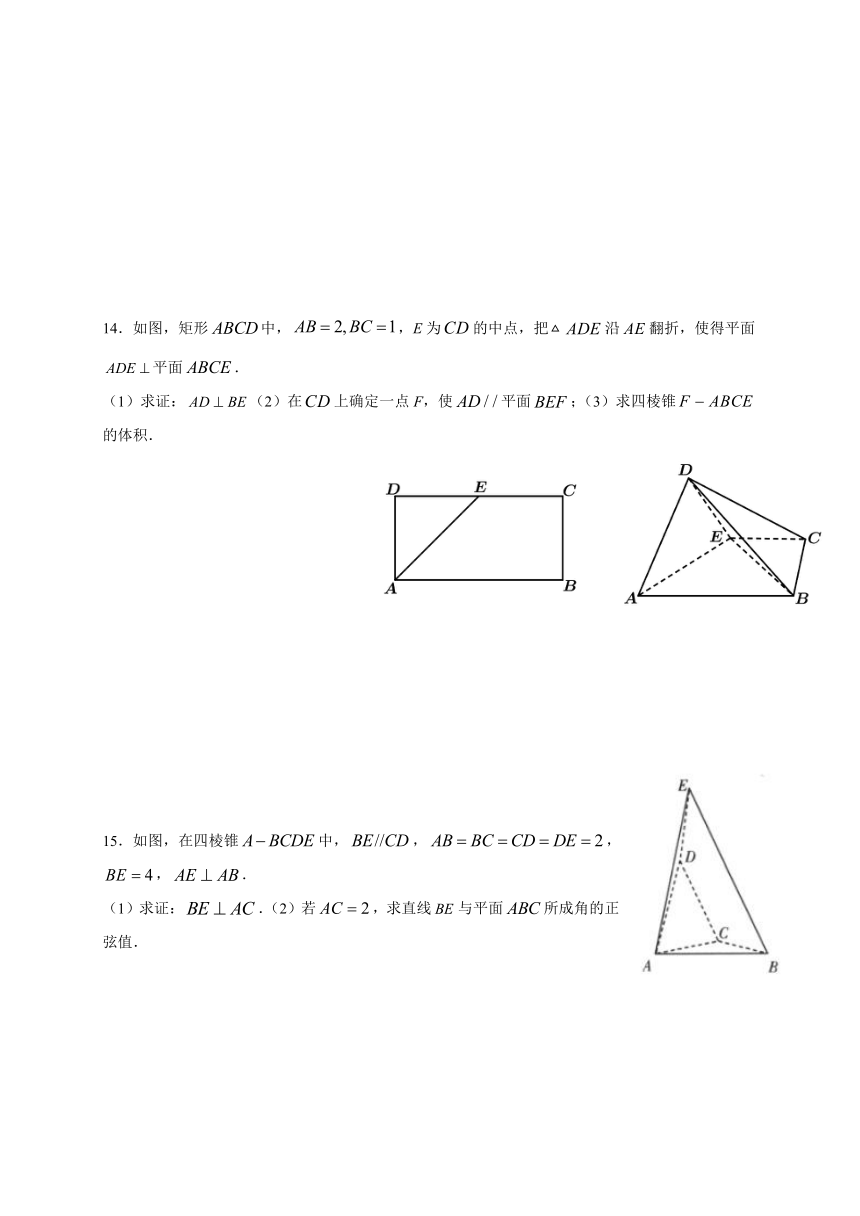
14.如图,矩形false中,false,E为false的中点,把falsefalse沿false翻折,使得平面false平面false.
(1)求证:false(2)在false上确定一点F,使false平面false;(3)求四棱锥false的体积.
238125057785
465772587630
15.如图,在四棱锥false中,false,false,false,false.
(1)求证:false.(2)若false,求直线false与平面false所成角的正弦值.
参考答案
1.B
【分析】
利用平面与平面的位置关系判断.
【详解】
若false内有无穷多条直线与false平行,则平面false与平面false相交或平行,故false不正确;
若false内的任何直线都与false平行,则false,故B正确;
若直线false在平面false内,直线false在平面false内,且false,false,则平面false与平面false相交或平行,故C不正确;
若直线false,直线false,则平面false与平面false相交或平行,故D不正确.
故选:B
2.A
【分析】
根据面面、线面、线线关系,结合面面平行的性质及平行线的性质,判断空间中线面、面面的位置关系,及线段的数量关系.
【详解】
A:平行于同一直线的两平面可能平行,也可能相交,不正确;
由面面平行的性质、及平行线的性质可知B、C、D正确;
故选:A.
3.D
【分析】
在false上取一点false,使得false,证得false,即可证得直线false不与false平行;构造经过直线false的平面,确定该平面与平面false的交线,判断false与交线的位置关系,即可判断选项B,C,D.
【详解】
如图,在false上取一点false,使得false,连接false,false,又false,
所以false,则直线false不与false平行.
连接false,false,交于点false,由四边形false是平行四边形得false为false,false的中点.
因为false,false分别为false,false的中点,所以false,
连接false,交false于点false,于是false,在线段false上取点false,使得false,连接false,因为false,所以false为false的中点,
又false,连接false,则false.
因为false,false,所以false,于是false,因此直线false与false异面,不与直线false平行,false平面false,
故选:D.
4.D
【分析】
根据直线平面间的位置关系或线面垂直的判定定理判断各选项.
【详解】
解:A:根据面面垂直的判定,当直线m,n相交时,才有false,∴A错误.
B:当false时,直线l与平面α可能平行,∴B错误.
C:当false时,直线l与平面α可能平行,也可能在平面α内,∴C错误.
D:当false时,根据两条平行线中的一条与平面垂直,则另一条也和这个平面垂直,
∴false,但反之不一定成立,∴D正确.
故选:D.
5.D
【分析】
取AD的中点G,连接EG,FG,可得∠FEG或其补角为EF与CD所成的角,在falseEFG中,通过计算可得答案.
【详解】
取AD的中点G,连接EG,FG.
∵E,F分别为AC,BD的中点,∴FGfalseAB,EGfalseCD,∠FEG或其补角为EF与CD所成的角.
∵EF⊥AB,∴在falseEFG中,EF⊥FG,
∴sin∠FEG=false=false,
∴∠FEG=30°.
故选:D
6.D
【分析】
把展开图还原成正方体可得false的位置关系.
【详解】
把展开图恢复成如图所示的正方体,
其中,false为等边三角形,所以false.选D.
【点睛】
已知空间几何体的平面展开图求原几何体中点线面的位置关系,可先选定一个底面,然后把展开图还原成空间几何体,在空间几何体中看指定的几何对象的位置关系,此类问题忌凭空想象.
7.A
【分析】
由题意设棱长为a,补正三棱柱ABC-A2B2C2,构造直角三角形A2BM,解直角三角形求出BM,利用勾股定理求出A2M,从而求解.
【详解】
设棱长为a,补正三棱柱ABC-A2B2C2(如图).
平移AB1至A2B,连接A2M,∠MBA2即为AB1与BM所成的角,
在△A2BM中,false
falsefalse .
故选A.
【点睛】
本题主要考查了异面直线及其所成的角和勾股定理的应用,计算比较复杂,要仔细的做.
8.A
【分析】
根据翻折过程中,始终false,false,利用面面平行的判定定理及性质,即可判定A正确;根据题中条件,得到false与false相交,可判断B错;根据题中条件,判定直线false与平面false相交,即可判定C错;根据题中条件,得到false与false不垂直,即可判定D错.
【详解】
对于false,由题意得:false,false,
∵false,false,∴平面false平面false,
∵false平面false,∴在翻折过程中,恒有直线false平面false,故A正确;
对于B,∵直线false将矩形false分为两个直角梯形false和false,
∴false与false相交,
∴不存在某一位置,使得false平面false,故B错误;
对于C,∵平面false平面false,false平面false,false,所以直线false与平面false相交;∴不存在某一位置,使得false,故C错误;
对于D,∵四边形false是梯形,false,
∴false与false不垂直,
∴不存在某一位置,使得false平面false,故D错误.
故选:A.
【点睛】
思路点睛:
判断线线、线面位置关系时,一般需要结合相关概念,以及判定定理与性质定理,由题中条件,进行判断即可.
9.①②④
【分析】
通过证明false平面false来证明false;将false的面积表示出来,等价于求PE长度的最值,从而在false中分别求得最大值和最小值;通过证明false平面false且false平面false来证明平面false平面false.
【详解】
在正方体false中,
false,
故false平面false,又false,
则false,①正确;
连接BD交AC与E,由false,则false,
false,则求false的面积的最值等价于求PE长度的最值.
在false中,当false时,false最小,易知false,false,
false,此时false,
此时,false的面积的最小值为false,故③错误;
当false与false重合时,false最大,易知false,false,
此时,false的面积的最大值为false,故②正确;
当false时,在false中,false,false,
则false,
则false,又false,
故false平面false,
由正方体体对角线性质,易知false,即false平面false,
故平面false平面false,④正确;
故答案为:①②④.
【点睛】
关键点点睛:利用正方体内的线线,线面,面面关系,来证明问题所求的线面,面面关系.
10.若false,false,则false.
【分析】
设过false有一个平面false,使得false,则由false结合线面平行的性质可得false,由false结合线面垂直的性质可得false,从而可得false
【详解】
若false,false,则false.
理由:设过false有一个平面false,使得false,
false,false,false,
false,
又false,false,可得false,
又false,可得false.
故答案为:若false,false,则false.
11.false或false
【分析】
取false的中点false,连接false、false,求出false的值,利用余弦定理可求得线段false的长.
【详解】
取false的中点false,连接false、false,
false、false分别为false、false的中点,false且false,
同理可得false且false,
false为异面直线false与false所成的角或其补角,则false或false.
在false中,false.
若false,则false为等边三角形,此时,false;
若false,由余弦定理可得false.
综上所述,false或false.
故答案为:false或false.
【点睛】
思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:
(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角;
(2)认定:证明作出的角就是所求异面直线所成的角;
(3)计算:求该角的值,常利用解三角形;
(4)取舍:由异面直线所成的角的取值范围是false,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.
12.false
【分析】
取false的中点false,false的中点false,连接false,可得四边形false是平行四边形,可得false,同理可得false,可得面面平行,进而得出false点轨迹为false.
【详解】
如图所示,false的中点false,false的中点false,连接false.
可得四边形false是平行四边形,∴false,又false平面false,false平面false,可得false平面false.同理可得false,false平面false,又false,∴平面false平面false.
∵false点是正方形false内的动点,false平面false,∴点false在线段false上.
∴false点的轨迹长度为false.
故答案为:false.
13.(1)证明见解析;(2)在false上是存在false中点false,使false平面false成立,证明见解析.
【分析】
(1)取false上靠近false的三等分点false,连接false,可得false进而证明false平面false,同理证明false平面false,得出面false平面false即可证明;
(2)存在false中点false,连false,使false,连false,得出false即可证明.
【详解】
(1)如图,取false上靠近false的三等分点false,连接false,
false中,false,
则false又false平面false,false平面false,
false平面false,同理,false平面false,又false,
∴平面false平面false,又false平面false,
∴false平面false.
(2)存在false中点false,使false平面false成立.
取false中点false,连false,使false,连false.
false是矩形,false是false的中点,
又false是false上靠近点false的一个三等分点,且false是false中点,
false是false的中点,
false中,false,
又false平面false,false平面false,
false平面false,
故在false上是存在false中点false,使false平面false成立.
【点睛】
关键点睛:本题考查线面平行的证明,解题的关键是正确理解线面平行的判定定理以及面面平行的性质.
14.(1)证明见解析;(2)线段false上取false的三等分点F(靠近C);(3)false.
【分析】
(1)先由勾股定理证明false,再由面面垂直的性质得出false平面false,进而由线面垂直的性质得出线线垂直;
(2)作辅助线并证明false,再由线面平行的判定定理求解即可;
(3)先由面面垂直的性质得出false平面false,进而确定四棱锥false的高,最后得出体积.
【详解】
(1)证明:∵平面false平面false,平面false平面false
又由已知可得false,false,∴false,则false平面false
∵false平面false,∴false,故false;
(2)连接false交false于G,则false,在线段false上取false的三等分点F(靠近C),
连接false,则false,可得false
而false平面false平面false,则false平面false;
(3)取false中点O,连接false,则false
又平面false平面false,且平面false平面false
∴false平面false,在false中,可得false
∵F为false的三等分点F(靠近C),∴F到平面false的距离为false.
可得四棱锥false的体积为false.
【点睛】
关键点睛:在第三问中,要求四棱锥false的体积,关键是想到四棱锥false和四棱锥false同底面,高成比例,从而得出四棱锥false的体积.
15.(1)证明见解析;(2)false.
【分析】
(1)取false的中点false,连接false,false,false,证明false,false,再利用线面垂直的判定定理证出false平面false,即证.
(2)过点false作false于点false,得出false为直线false与平面false所成的角,在false中,利用余弦定理即可求解.
【详解】
(1)如图,取false的中点false,连接false,false,false,
∵false,∴false.
∵false,false,false,
∴四边形false为等腰梯形,且false.
∵false,false,false,∴false,
∴false,∴false.
∵false,false平面false,false,
∴false平面false,
又false平面false,∴false.
(2)由(1)知false平面false,
又false平面false,∴平面false平面false.
∵平面false平面false,
∴过点false作false于点false,则false平面false,
∴false为直线false与平面false所成的角.
在等边三角形false中,易得false.
在false中,false,false,∴false.
又false,∴在false中,false,
∴false,
即直线false与平面false所成角的正弦值为false.
【点睛】
方法点睛:证明线线垂直常由线面垂直的性质推理得到,一条直线和一个平面垂直,这条直线就垂直于这个平面内的所有直线,这是证明线线垂直的重要方法,若已知条件中含边的长度,则可根据线段间的数量关系,利用勾股定理的逆定理或三角形三线合一的性质来证明线线垂直.
一、单选题
1.平面false与平面false平行的条件可以是( )
A.false内有无穷多条直线与false平行 B.false内的任何直线都与false平行
C.直线false在平面false内,直线false在平面false内,且false,falseD.直线false,直线false
51816001219202.下列命题中,错误的是( )
A.平行于同一直线的两个平面互相平行 B.平行于同一平面的两个平面互相平行
C.若一条直线与两个平行平面中的一个相交,则这条直线与另一个平面也相交
D.夹在两平行平面间的平行线段相等
56388002057403.如图,在四棱锥false中,底面false是平行四边形,点false,false分别是false,false的中点,点false在线段false上,且false,则( )
A.false B.直线false与直线false相交 C.false D.false平面false
4.若false是两个不同的平面,l,m,n是三条不同的直线,则false成立的充分不必要条件是
5667375150495A.false B.false C.falseD.false
5.在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为( )A.90° B.45° C.60° D.30°
5505450171456.如图所示,将无盖正方体纸盒展开,直线AB、CD在原正方体中的位置关系是( )
A.平行 B.相交且垂直 C.异面直线 D.相交成60°角
7.如图,已知三棱柱false的各条棱长都相等,且false底面false,false是侧棱false的中点,则异面直线false和false所成的角为( )
4819650304800A.false B. C. D.false
8.如图1,直线false将矩形false分为两个直角梯形false和false,将梯形false沿边false翻折,如图2,在翻折过程中(平面false和平面false不重合),下列说法正确的是( )
A.在翻折过程中,恒有直线false平面false B.存在某一位置,使得false平面false
C.存在某一位置,使得false D.存在某一位置,使得false平面false
二、填空题
9.如图,在边长为2的正方体false中,点P是该正方体对角线false上的动点,给出下列四个结论:
468630069215①false②false面积的最大值是false
③false面积的最小值是false④当false时,平面false平面false
其中所有正确结论的序号是___________.
53911503619510.已知false,false是平面false外的两条不同直线,给出下列三个论断:①false;②false;③false.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:
522922566484511.如图,在四面体false中,false,false与false所成的角为false,false、false分别为false、false的中点,则线段false的长为________.
12.如图所示,正方体false的棱长为false,false为false的中点,false点是正方形false内的动点,若false平面false,则false点的轨迹长度为______.
三、解答题
13.如图,在四棱锥false中,底面false是矩形.
(1)设false为false上靠近false的三等分点,false为false上靠近false的三等分点.求证:false平面false.
(2)设false是false上靠近点false的一个三等分点,试问:在false上是否存在一点false,使false平面false成立?若存在,请予以证明;若不存在,说明理由.
3390900653415
14.如图,矩形false中,false,E为false的中点,把falsefalse沿false翻折,使得平面false平面false.
(1)求证:false(2)在false上确定一点F,使false平面false;(3)求四棱锥false的体积.
238125057785
465772587630
15.如图,在四棱锥false中,false,false,false,false.
(1)求证:false.(2)若false,求直线false与平面false所成角的正弦值.
参考答案
1.B
【分析】
利用平面与平面的位置关系判断.
【详解】
若false内有无穷多条直线与false平行,则平面false与平面false相交或平行,故false不正确;
若false内的任何直线都与false平行,则false,故B正确;
若直线false在平面false内,直线false在平面false内,且false,false,则平面false与平面false相交或平行,故C不正确;
若直线false,直线false,则平面false与平面false相交或平行,故D不正确.
故选:B
2.A
【分析】
根据面面、线面、线线关系,结合面面平行的性质及平行线的性质,判断空间中线面、面面的位置关系,及线段的数量关系.
【详解】
A:平行于同一直线的两平面可能平行,也可能相交,不正确;
由面面平行的性质、及平行线的性质可知B、C、D正确;
故选:A.
3.D
【分析】
在false上取一点false,使得false,证得false,即可证得直线false不与false平行;构造经过直线false的平面,确定该平面与平面false的交线,判断false与交线的位置关系,即可判断选项B,C,D.
【详解】
如图,在false上取一点false,使得false,连接false,false,又false,
所以false,则直线false不与false平行.
连接false,false,交于点false,由四边形false是平行四边形得false为false,false的中点.
因为false,false分别为false,false的中点,所以false,
连接false,交false于点false,于是false,在线段false上取点false,使得false,连接false,因为false,所以false为false的中点,
又false,连接false,则false.
因为false,false,所以false,于是false,因此直线false与false异面,不与直线false平行,false平面false,
故选:D.
4.D
【分析】
根据直线平面间的位置关系或线面垂直的判定定理判断各选项.
【详解】
解:A:根据面面垂直的判定,当直线m,n相交时,才有false,∴A错误.
B:当false时,直线l与平面α可能平行,∴B错误.
C:当false时,直线l与平面α可能平行,也可能在平面α内,∴C错误.
D:当false时,根据两条平行线中的一条与平面垂直,则另一条也和这个平面垂直,
∴false,但反之不一定成立,∴D正确.
故选:D.
5.D
【分析】
取AD的中点G,连接EG,FG,可得∠FEG或其补角为EF与CD所成的角,在falseEFG中,通过计算可得答案.
【详解】
取AD的中点G,连接EG,FG.
∵E,F分别为AC,BD的中点,∴FGfalseAB,EGfalseCD,∠FEG或其补角为EF与CD所成的角.
∵EF⊥AB,∴在falseEFG中,EF⊥FG,
∴sin∠FEG=false=false,
∴∠FEG=30°.
故选:D
6.D
【分析】
把展开图还原成正方体可得false的位置关系.
【详解】
把展开图恢复成如图所示的正方体,
其中,false为等边三角形,所以false.选D.
【点睛】
已知空间几何体的平面展开图求原几何体中点线面的位置关系,可先选定一个底面,然后把展开图还原成空间几何体,在空间几何体中看指定的几何对象的位置关系,此类问题忌凭空想象.
7.A
【分析】
由题意设棱长为a,补正三棱柱ABC-A2B2C2,构造直角三角形A2BM,解直角三角形求出BM,利用勾股定理求出A2M,从而求解.
【详解】
设棱长为a,补正三棱柱ABC-A2B2C2(如图).
平移AB1至A2B,连接A2M,∠MBA2即为AB1与BM所成的角,
在△A2BM中,false
falsefalse .
故选A.
【点睛】
本题主要考查了异面直线及其所成的角和勾股定理的应用,计算比较复杂,要仔细的做.
8.A
【分析】
根据翻折过程中,始终false,false,利用面面平行的判定定理及性质,即可判定A正确;根据题中条件,得到false与false相交,可判断B错;根据题中条件,判定直线false与平面false相交,即可判定C错;根据题中条件,得到false与false不垂直,即可判定D错.
【详解】
对于false,由题意得:false,false,
∵false,false,∴平面false平面false,
∵false平面false,∴在翻折过程中,恒有直线false平面false,故A正确;
对于B,∵直线false将矩形false分为两个直角梯形false和false,
∴false与false相交,
∴不存在某一位置,使得false平面false,故B错误;
对于C,∵平面false平面false,false平面false,false,所以直线false与平面false相交;∴不存在某一位置,使得false,故C错误;
对于D,∵四边形false是梯形,false,
∴false与false不垂直,
∴不存在某一位置,使得false平面false,故D错误.
故选:A.
【点睛】
思路点睛:
判断线线、线面位置关系时,一般需要结合相关概念,以及判定定理与性质定理,由题中条件,进行判断即可.
9.①②④
【分析】
通过证明false平面false来证明false;将false的面积表示出来,等价于求PE长度的最值,从而在false中分别求得最大值和最小值;通过证明false平面false且false平面false来证明平面false平面false.
【详解】
在正方体false中,
false,
故false平面false,又false,
则false,①正确;
连接BD交AC与E,由false,则false,
false,则求false的面积的最值等价于求PE长度的最值.
在false中,当false时,false最小,易知false,false,
false,此时false,
此时,false的面积的最小值为false,故③错误;
当false与false重合时,false最大,易知false,false,
此时,false的面积的最大值为false,故②正确;
当false时,在false中,false,false,
则false,
则false,又false,
故false平面false,
由正方体体对角线性质,易知false,即false平面false,
故平面false平面false,④正确;
故答案为:①②④.
【点睛】
关键点点睛:利用正方体内的线线,线面,面面关系,来证明问题所求的线面,面面关系.
10.若false,false,则false.
【分析】
设过false有一个平面false,使得false,则由false结合线面平行的性质可得false,由false结合线面垂直的性质可得false,从而可得false
【详解】
若false,false,则false.
理由:设过false有一个平面false,使得false,
false,false,false,
false,
又false,false,可得false,
又false,可得false.
故答案为:若false,false,则false.
11.false或false
【分析】
取false的中点false,连接false、false,求出false的值,利用余弦定理可求得线段false的长.
【详解】
取false的中点false,连接false、false,
false、false分别为false、false的中点,false且false,
同理可得false且false,
false为异面直线false与false所成的角或其补角,则false或false.
在false中,false.
若false,则false为等边三角形,此时,false;
若false,由余弦定理可得false.
综上所述,false或false.
故答案为:false或false.
【点睛】
思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:
(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角;
(2)认定:证明作出的角就是所求异面直线所成的角;
(3)计算:求该角的值,常利用解三角形;
(4)取舍:由异面直线所成的角的取值范围是false,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.
12.false
【分析】
取false的中点false,false的中点false,连接false,可得四边形false是平行四边形,可得false,同理可得false,可得面面平行,进而得出false点轨迹为false.
【详解】
如图所示,false的中点false,false的中点false,连接false.
可得四边形false是平行四边形,∴false,又false平面false,false平面false,可得false平面false.同理可得false,false平面false,又false,∴平面false平面false.
∵false点是正方形false内的动点,false平面false,∴点false在线段false上.
∴false点的轨迹长度为false.
故答案为:false.
13.(1)证明见解析;(2)在false上是存在false中点false,使false平面false成立,证明见解析.
【分析】
(1)取false上靠近false的三等分点false,连接false,可得false进而证明false平面false,同理证明false平面false,得出面false平面false即可证明;
(2)存在false中点false,连false,使false,连false,得出false即可证明.
【详解】
(1)如图,取false上靠近false的三等分点false,连接false,
false中,false,
则false又false平面false,false平面false,
false平面false,同理,false平面false,又false,
∴平面false平面false,又false平面false,
∴false平面false.
(2)存在false中点false,使false平面false成立.
取false中点false,连false,使false,连false.
false是矩形,false是false的中点,
又false是false上靠近点false的一个三等分点,且false是false中点,
false是false的中点,
false中,false,
又false平面false,false平面false,
false平面false,
故在false上是存在false中点false,使false平面false成立.
【点睛】
关键点睛:本题考查线面平行的证明,解题的关键是正确理解线面平行的判定定理以及面面平行的性质.
14.(1)证明见解析;(2)线段false上取false的三等分点F(靠近C);(3)false.
【分析】
(1)先由勾股定理证明false,再由面面垂直的性质得出false平面false,进而由线面垂直的性质得出线线垂直;
(2)作辅助线并证明false,再由线面平行的判定定理求解即可;
(3)先由面面垂直的性质得出false平面false,进而确定四棱锥false的高,最后得出体积.
【详解】
(1)证明:∵平面false平面false,平面false平面false
又由已知可得false,false,∴false,则false平面false
∵false平面false,∴false,故false;
(2)连接false交false于G,则false,在线段false上取false的三等分点F(靠近C),
连接false,则false,可得false
而false平面false平面false,则false平面false;
(3)取false中点O,连接false,则false
又平面false平面false,且平面false平面false
∴false平面false,在false中,可得false
∵F为false的三等分点F(靠近C),∴F到平面false的距离为false.
可得四棱锥false的体积为false.
【点睛】
关键点睛:在第三问中,要求四棱锥false的体积,关键是想到四棱锥false和四棱锥false同底面,高成比例,从而得出四棱锥false的体积.
15.(1)证明见解析;(2)false.
【分析】
(1)取false的中点false,连接false,false,false,证明false,false,再利用线面垂直的判定定理证出false平面false,即证.
(2)过点false作false于点false,得出false为直线false与平面false所成的角,在false中,利用余弦定理即可求解.
【详解】
(1)如图,取false的中点false,连接false,false,false,
∵false,∴false.
∵false,false,false,
∴四边形false为等腰梯形,且false.
∵false,false,false,∴false,
∴false,∴false.
∵false,false平面false,false,
∴false平面false,
又false平面false,∴false.
(2)由(1)知false平面false,
又false平面false,∴平面false平面false.
∵平面false平面false,
∴过点false作false于点false,则false平面false,
∴false为直线false与平面false所成的角.
在等边三角形false中,易得false.
在false中,false,false,∴false.
又false,∴在false中,false,
∴false,
即直线false与平面false所成角的正弦值为false.
【点睛】
方法点睛:证明线线垂直常由线面垂直的性质推理得到,一条直线和一个平面垂直,这条直线就垂直于这个平面内的所有直线,这是证明线线垂直的重要方法,若已知条件中含边的长度,则可根据线段间的数量关系,利用勾股定理的逆定理或三角形三线合一的性质来证明线线垂直.
同课章节目录
