福建省福州市平潭县新世纪学校2020-2021学年高一下学期5月周练(12)数学试题 Word版含答案
文档属性
| 名称 | 福建省福州市平潭县新世纪学校2020-2021学年高一下学期5月周练(12)数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 672.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 09:35:04 | ||
图片预览




文档简介
平潭县新世纪学校2020-2021学年高一下学期数学周练(12)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.设false是两个不同平面,false是两条直线,下列命题中正确的是( )
A.如果false,false,false,那么falseB.如果false,false,false,那么false
C.如果false,false,false,那么false
D.如果false,false与false所成的角和false与false所成的角相等,那么false
2.不同的直线false和false,不同的平面false,false,false,下列条件中能推出false的是( )
4686300154305A.false,false,false B.false,false
C.false,false,false D.false,false,false
3.如图所示,已知false平面ABC,false,false,则PC等于( )A.6 B.4 C.12 D.144
4.在正方体false中,false是正方形false的中心,则直线false与直线false所成角大小为( )A.30° B.45° C.60° D.90°
44005502438405.直三棱柱false中,false,false,则false与面false成角的正弦值为( )A.false B.false C.false D.false
6.如图,在棱长为1的正方体false中,false为线段false上的动点,下列说法不正确的是( )
A.对任意点false,false平面falseB.三棱锥false的体积为false
C.线段false长度的最小值为falseD.存在点false,使得false与平面false所成角的大小为false
5124450349257.如图所示,AB是⊙O的直径,VA垂直于⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是( )
A.MNfalseAB B.MN与BC所成的角为45°
C.OCfalse平面VAC D.平面VACfalse平面VBC
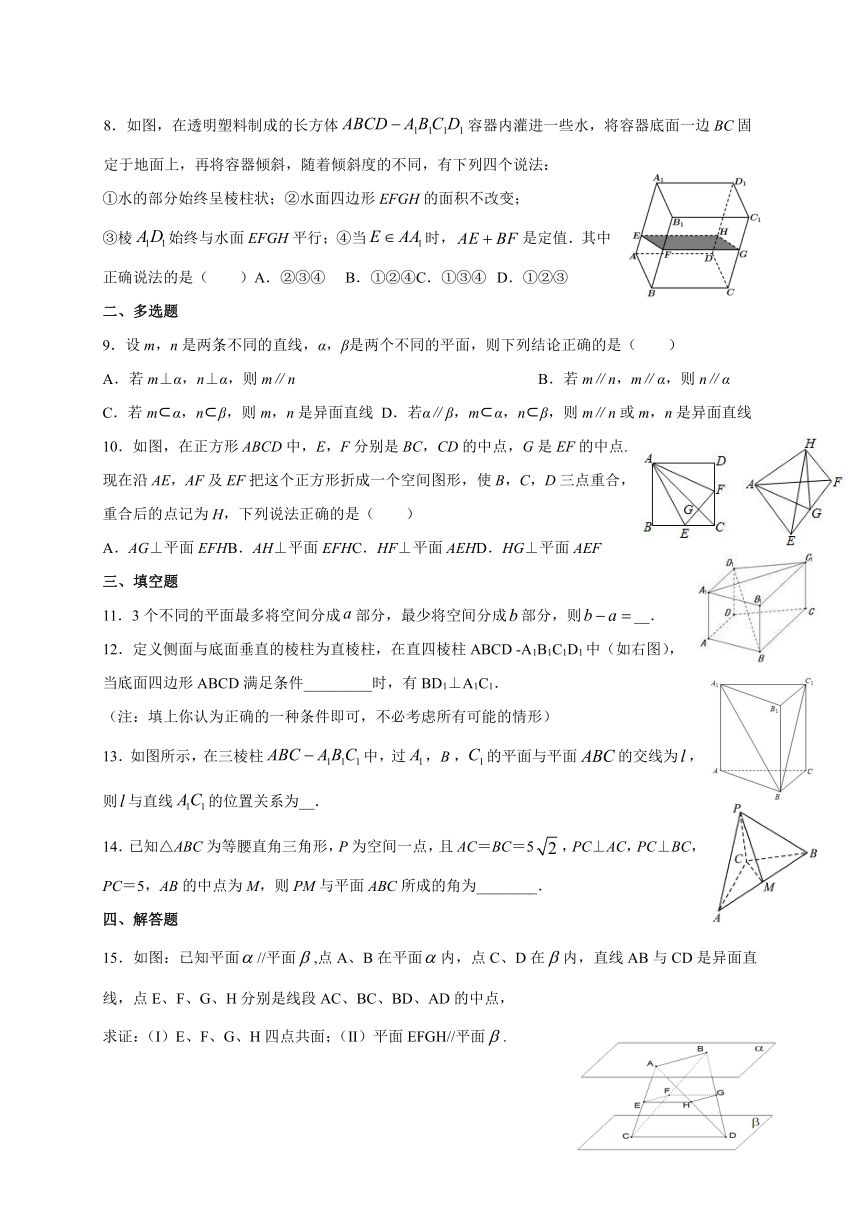
8.如图,在透明塑料制成的长方体false容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
4591050-86995①水的部分始终呈棱柱状;②水面四边形EFGH的面积不改变;
③棱false始终与水面EFGH平行;④当false时,false是定值.其中正确说法的是( )A.②③④ B.①②④C.①③④ D.①②③
二、多选题
9.设m,n是两条不同的直线,α,β是两个不同的平面,则下列结论正确的是( )
A.若m⊥α,n⊥α,则m∥n B.若m∥n,m∥α,则n∥α
C.若m?α,n?β,则m,n是异面直线 D.若α∥β,m?α,n?β,则m∥n或m,n是异面直线
47339256159510.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( )
5229225143510A.AG⊥平面EFHB.AH⊥平面EFHC.HF⊥平面AEHD.HG⊥平面AEF
三、填空题
11.3个不同的平面最多将空间分成false部分,最少将空间分成false部分,则false__.
533400038862012.定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD -A1B1C1D1中(如右图),当底面四边形ABCD满足条件_________时,有BD1⊥A1C1.
(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)
535305060388513.如图所示,在三棱柱false中,过false,false,false的平面与平面false的交线为false,则false与直线false的位置关系为__.
14.已知△ABC为等腰直角三角形,P为空间一点,且AC=BC=5false,PC⊥AC,PC⊥BC,PC=5,AB的中点为M,则PM与平面ABC所成的角为________.
四、解答题
15.如图:已知平面false//平面false,点A、B在平面false内,点C、D在false内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
4133850201295求证:(Ⅰ)E、F、G、H四点共面;(Ⅱ)平面EFGH//平面false.
16.如图,四棱锥false的底面是边长为2的菱形,false底面false.
(1)求证:false平面PBD;
(2)若false,直线false与平面false所成的角为45°,求四棱锥false的体积.
4210050394335
17.如图,四棱锥false中,底面false为矩形,false底面false,E为false的中点.
(1)证明:false平面false;
3971925121920(2)设false,false,四棱锥false的体积为1,求证:平面false平面false.
参考答案
1.C
【分析】
A.由false,false,得到false或false,再利用平行于同一直线的两平面的位置关系判断;B. 由false,false,得到false或false,再利用面面垂直的判定定理判断; C. 由false,false,得到false,再利用垂直于同一直线的两平面平行判断;D.利用空间直线的位置关系判断.
【详解】
A.因为false,false,所以false或false,又false,则false位置不确定,故错误;
B.因为false,false,所以false或false,又false,所以false,故错误;
C. 因为false,false,所以false,又false,所以false,故正确;
D.如果false,false与false所成的角和false与false所成的角相等,那么false,相交或异面,故错误.
故选:C
2.C
【分析】
利用平面与平面的位置关系判断.
【详解】
由不同的直线false和false,不同的平面false,false,false,知:
若false,false,false,则false与false相交或平行,故false不正确;
若false,false,则false与false相交或平行,故B不正确;
若false,false,false,则由平面平行的判定定理知false,故C正确;
若false,false,false,则false与false相交或平行,故D不正确.
故选:C.
3.C
【分析】
由余弦定理求得false,由线面垂直的性质定理得线线垂直,由勾股定理求得false.
【详解】
连接false,false,
false,
false由余弦定理可得false,
false平面false,false平面false,
false,
false.
故选:C.
4.A
【分析】
如图,连接false,false,false,利用余弦定理可求false的值,从而可得直线false与直线false所成角大小.
【详解】
设正方体的棱长为false,连接false,false,false,
因为false,故false或其补角为直线false与直线false所成角.
而false,false,false,
故false,所以false,
所以false,因为false为锐角,故false,
故选:A.
5.A
【分析】
过false作false,可证false平面false,连接false,可知false即为所求线面角,计算即可求解.
【详解】
如图,过false作false,连接false,
在直三棱柱false中,因为falsefalse
所以false平面false,
故false在平面false上的射影为false,
所以false为直线false与平面false所成的角,
设false,又false
所以falsefalse
故false
故选:A
【点睛】
方法点晴:求线面夹角一般有两种方法:
(1)几何法:作平面的垂线,找到夹角再用三角函数求解;
(2)向量法:建系用空间向量公式求解.
6.D
【分析】
连接false,证得平面false平面false,可判定A正确;根据false,可判定B正确;当点false为线段false的中点时,求得线段false的长度最小值,可判定C正确;求得false与平面false所成角的正切值的取值范围,可判定D错误.
【详解】
连接false,由false且false,
可得四边形false为平行四边形,所以false,
又由false平面false,且false平面false,所以false平面false,
同理可得false平面false,又false,可得平面false平面false,
所以对于任意点false,则false平面false,所以A正确;
由false,所以B正确;
当点false为线段false的中点时,可得false,
此时线段false的长度最小,最小值为false,所以C正确;
当点false在线段false上运动时,false长度的最小值为false,最大值为false,
又由false长度的取值范围为false,而点false到平面false的距离为定值1,
因为平面false平面false,
所以false与平面false所成角与false与平面false所成角相等,
又由false平面false,可得false在平面false射影为false,
所以false在平面false所成角的正切值为false,
即false与平面false所成角的正切值的取值范围为false,
其最大值小于false,则不存在点false使得false与平面false所成角的大小为false,
所以D错误.
故选:D.
【点睛】
1、对面面平行判定定理的条件“面内两相交直线”认识不清导致错解;
2、等体积法:等体积法也称积转化或等积变形,通过选择合适的底面来求几何体体积的一种方法,多用来解决锥体的体积,特别时三棱锥的体积.
3、求解直线与平面所成角时,根据直线与平面所成角的定义,结合垂线段与斜线段的长度比求得线面角的正弦值.
7.D
【分析】
由中位线性质,平移异面直线即可判断MN不与AB平行,根据异面直线平面角知MN与BC所成的角为90°,应用反证知OC不与平面VAC垂直,由面面垂直的判定知面VACfalse面VBC,即可知正确选项.
【详解】
M,N分别为VA,VC的中点,在△false中有false,
在面false中false,MN不与AB平行;
false,知:MN与BC所成的角为false;
因为false面false,false与平面内交线false都不垂直,OC不与平面VAC垂直;
由false面false,false面false即false,而false知false,false有falsefalse面false,又false面false,所以面falsefalse面false;
故选:D
【点睛】
本题考查了异面直线的位置关系、夹角,以及线面垂直的性质,面面垂直判定的应用,属于基础题.
8.C
【分析】
①由平面false平行平面false判断;②由四边形false为矩形,false变化而false不变判断;③由false始终与EH平行判断;④由水的体积是定值,高不变,底面面积不变判断.
【详解】
①由棱柱的特征知:平面false平行平面false,故正确;
②因为四边形false是矩形,false的长度变化,false长度不变,所以面积是改变的,故错误;
③因为false,false平面EFGH,false平面EFGH,所以false平面EFGH,故正确;
④因为水的体积是定值,高不变,所以底面面积不变,所以false时,false是定值.故正确.
故选:C.
9.AD
【分析】
利用线面垂直的判定,线面平行的判定,线线的位置关系及面面平行的性质逐一判断即可.
【详解】
由m,n是两条不同的直线,α,β是两个不同的平面,得:
对于A,若m⊥α,n⊥α,则由线面垂直的性质定理得m∥n,故A正确;
对于B,若m∥n,m∥α,则n∥α或n?α,故B错误;
对于C,若m?α,n?β,则m,n相交、平行或异面,故C错误;
对于D,若α∥β,m?α,n?β,则m∥n或m,n是异面直线,故D正确.
故选:AD.
【点睛】
本题主要考查了线面垂直的性质,线面平行的判定和面面平行的性质.
10.BC
【分析】
由题意可得,AH⊥HE,AH⊥HF,HF⊥HE,从而利用线面垂直的判定定理可得AH⊥平面EFH,HF⊥平面AHE,进而可得答案
【详解】
解:由题意可得:AH⊥HE,AH⊥HF.
∴AH⊥平面EFH,而AG与平面EFH不垂直.∴B正确,A不正确.
又HF⊥HE,∴HF⊥平面AHE,C正确.
HG与AG不垂直,因此HG⊥平面AEF不正确.D不正确.
故选:BC.
【点睛】
此题考查线面垂直的判定,考查折叠问题,属于基础题
11.false
【分析】
对平面的位置关系分类讨论,即可得到答案.
【详解】
当三个不同的平面互相平行时,最少将空间分成4部分,即false,
当三个平面三维放置时,最多将空间分成8部分,即false,
所以false.
故答案为:false
【点睛】
方法点睛:对平面分空间为几个部分问题,要有画图的意识,结合空间想象能力全方位、多角度地去考虑问题,作出判断.
12.对角线垂直(底面是菱形、正方形皆可).
【解析】
试题分析::∵四棱柱ABCD -A1B1C1D1是直棱柱,∴false,若false,
则false⊥平面false,∴false⊥AC,又由false∥BD,则有BD⊥AC,
反之,由BD⊥AC亦可得到false
考点:空间中直线与直线之间的位置关系
13.平行
【分析】
利用线面平行的判定定理和线面平行的性质定理,即可判断出false与直线false平行.
【详解】
在三棱柱false中,false,false平面false,false平面false,
所以false平面false,又因为false平面false,且平面false平面false,
所以false.
故答案为:平行
14.45°
【分析】
由线面垂直找出AM在面ABC内射影得线面角,在△PCM中计算而得.
【详解】
∵PC⊥AC,PC⊥BC,AC∩BC=C,∴PC⊥平面ABC,
∴PM在平面ABC内的射影为CM,故∠PMC为PM与平面ABC所成的角.
∵AC=BC=5false,∠ACB=90°,而AB的中点为M,
∴CM=5,又PC=5,∴△PCM为等腰直角三角形,
∴∠PMC=45°,即PM与平面ABC所成的角为45°.
故答案为:45°
15.(Ⅰ)∵点E、F是线段AC、BC的中点,∴EF∥AB,
又∵G、H是线段BD、AD的中点,∴GH∥AB,
∴EF∥GH, 因此: E、F、G、H四点共面;
(Ⅱ)∵平面false//平面false,点A、B在平面false内,∴AB//平面false
设平面ABC与平面false的交线为CP,
∵直线AB与CD是异面直线, ∴CP与CD是交线,
∵AB//平面false, ∴AB//CP, 又EF∥AB, ∴EF//CP,∴EF∥平面false,
∵点E、H是线段AC、AD的中点,∴EH∥CD, ∴EH∥平面false,
因此:平面EFGH//平面false
【解析】
考点:平面与平面平行的判定.
分析:(Ⅰ)根据中位线定理可知EF∥AB,GH∥AB,从而EF∥GH,根据公理可知两平行线确定一平面,则E、F、G、H四点共面;
(Ⅱ)根据平面α∥平面β,点A、B在平面α内,则AB∥平面α,设平面ABC与平面β的交线为CP,根据AB∥平面α,则AB∥CP,又EF∥AB,则EF∥CP,根据线面平行的判定定理可知EF∥平面β,根据中位线定理可知EH∥CD,从而EH∥平面β,最后根据面面平行的判定定理可平面EFGH∥平面β.
解答:证:(Ⅰ)∵点E、F是线段AC、BC的中点,
∴EF∥AB,
又∵G、H是线段BD、AD的中点,∴GH∥AB,
∴EF∥GH,因此:E、F、G、H四点共面;
(Ⅱ)∵平面α∥平面β,点A、B在平面α内,∴AB∥平面α
设平面ABC与平面β的交线为CP,
∵直线AB与CD是异面直线,
∴CP与CD是交线,
∵AB∥平面α,∴AB∥CP,又EF∥AB,
∴EF∥CP,∴EF∥平面β,
∵点E、H是线段AC、AD的中点,
∴EH∥CD,∴EH∥平面β,
因此:平面EFGH∥平面β.
点评:本题考查证明两个平面平行的方法:在一个平面内找到两条条相交的直线和另一个平面平行,属于基础题.
16.(1)证明见解析;(2)false
【分析】
(1)通过AC⊥BD与PD⊥AC可得false平面false;
(2)由题先得出∠PBD是直线PB与平面ABCD所成的角,即∠PBD=45°,则可先求出菱形ABCD的面积,进而可得四棱锥P- ABCD的体积.
【详解】
解:(1)因为四边形ABCD是菱形,所以AC⊥BD,
又因为PD⊥平面ABCD,false平面ABCD,
所以PD⊥AC,又false,
故AC⊥平面PBD;
(2)因为PD⊥平面ABCD,
所以∠PBD是直线PB与平面ABCD所成的角,
于是∠PBD=45°,
因此BD=PD=2.又AB= AD=2,
所以菱形ABCD的面积为false,
故四棱锥P- ABCD的体积false.
17.(1)证明见解析;(2)证明见解析.
【分析】
( 1)设false与false的交点为false,连接false,通过直线与平面平行的判定定理证明false平面false;
( 2)通过体积得到底面为正方形,再由线面垂直得到面面垂直即可.
【详解】
(1)连接false交false于点O,连结false,
因为false为矩形,所以O为false的中点,
又E为false的中点,所以false,
false平面false,false平面false,所以false平面false.
(2)因为false,
所以false,所以底面false为正方形,所以false,
因为false,所以false,且false,所以false平面false,
又false平面false,所以平面false平面false.
【点睛】
本题主要考查了立体几何及其运算,要证明线面平行先证明线线平行,要证明面面垂直,先证明线面垂直,考查了学生的基础知识、空间想象力.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.设false是两个不同平面,false是两条直线,下列命题中正确的是( )
A.如果false,false,false,那么falseB.如果false,false,false,那么false
C.如果false,false,false,那么false
D.如果false,false与false所成的角和false与false所成的角相等,那么false
2.不同的直线false和false,不同的平面false,false,false,下列条件中能推出false的是( )
4686300154305A.false,false,false B.false,false
C.false,false,false D.false,false,false
3.如图所示,已知false平面ABC,false,false,则PC等于( )A.6 B.4 C.12 D.144
4.在正方体false中,false是正方形false的中心,则直线false与直线false所成角大小为( )A.30° B.45° C.60° D.90°
44005502438405.直三棱柱false中,false,false,则false与面false成角的正弦值为( )A.false B.false C.false D.false
6.如图,在棱长为1的正方体false中,false为线段false上的动点,下列说法不正确的是( )
A.对任意点false,false平面falseB.三棱锥false的体积为false
C.线段false长度的最小值为falseD.存在点false,使得false与平面false所成角的大小为false
5124450349257.如图所示,AB是⊙O的直径,VA垂直于⊙O所在的平面,点C是圆周上不同于A,B的任意一点,M,N分别为VA,VC的中点,则下列结论正确的是( )
A.MNfalseAB B.MN与BC所成的角为45°
C.OCfalse平面VAC D.平面VACfalse平面VBC
8.如图,在透明塑料制成的长方体false容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
4591050-86995①水的部分始终呈棱柱状;②水面四边形EFGH的面积不改变;
③棱false始终与水面EFGH平行;④当false时,false是定值.其中正确说法的是( )A.②③④ B.①②④C.①③④ D.①②③
二、多选题
9.设m,n是两条不同的直线,α,β是两个不同的平面,则下列结论正确的是( )
A.若m⊥α,n⊥α,则m∥n B.若m∥n,m∥α,则n∥α
C.若m?α,n?β,则m,n是异面直线 D.若α∥β,m?α,n?β,则m∥n或m,n是异面直线
47339256159510.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点.现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,下列说法正确的是( )
5229225143510A.AG⊥平面EFHB.AH⊥平面EFHC.HF⊥平面AEHD.HG⊥平面AEF
三、填空题
11.3个不同的平面最多将空间分成false部分,最少将空间分成false部分,则false__.
533400038862012.定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD -A1B1C1D1中(如右图),当底面四边形ABCD满足条件_________时,有BD1⊥A1C1.
(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)
535305060388513.如图所示,在三棱柱false中,过false,false,false的平面与平面false的交线为false,则false与直线false的位置关系为__.
14.已知△ABC为等腰直角三角形,P为空间一点,且AC=BC=5false,PC⊥AC,PC⊥BC,PC=5,AB的中点为M,则PM与平面ABC所成的角为________.
四、解答题
15.如图:已知平面false//平面false,点A、B在平面false内,点C、D在false内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
4133850201295求证:(Ⅰ)E、F、G、H四点共面;(Ⅱ)平面EFGH//平面false.
16.如图,四棱锥false的底面是边长为2的菱形,false底面false.
(1)求证:false平面PBD;
(2)若false,直线false与平面false所成的角为45°,求四棱锥false的体积.
4210050394335
17.如图,四棱锥false中,底面false为矩形,false底面false,E为false的中点.
(1)证明:false平面false;
3971925121920(2)设false,false,四棱锥false的体积为1,求证:平面false平面false.
参考答案
1.C
【分析】
A.由false,false,得到false或false,再利用平行于同一直线的两平面的位置关系判断;B. 由false,false,得到false或false,再利用面面垂直的判定定理判断; C. 由false,false,得到false,再利用垂直于同一直线的两平面平行判断;D.利用空间直线的位置关系判断.
【详解】
A.因为false,false,所以false或false,又false,则false位置不确定,故错误;
B.因为false,false,所以false或false,又false,所以false,故错误;
C. 因为false,false,所以false,又false,所以false,故正确;
D.如果false,false与false所成的角和false与false所成的角相等,那么false,相交或异面,故错误.
故选:C
2.C
【分析】
利用平面与平面的位置关系判断.
【详解】
由不同的直线false和false,不同的平面false,false,false,知:
若false,false,false,则false与false相交或平行,故false不正确;
若false,false,则false与false相交或平行,故B不正确;
若false,false,false,则由平面平行的判定定理知false,故C正确;
若false,false,false,则false与false相交或平行,故D不正确.
故选:C.
3.C
【分析】
由余弦定理求得false,由线面垂直的性质定理得线线垂直,由勾股定理求得false.
【详解】
连接false,false,
false,
false由余弦定理可得false,
false平面false,false平面false,
false,
false.
故选:C.
4.A
【分析】
如图,连接false,false,false,利用余弦定理可求false的值,从而可得直线false与直线false所成角大小.
【详解】
设正方体的棱长为false,连接false,false,false,
因为false,故false或其补角为直线false与直线false所成角.
而false,false,false,
故false,所以false,
所以false,因为false为锐角,故false,
故选:A.
5.A
【分析】
过false作false,可证false平面false,连接false,可知false即为所求线面角,计算即可求解.
【详解】
如图,过false作false,连接false,
在直三棱柱false中,因为falsefalse
所以false平面false,
故false在平面false上的射影为false,
所以false为直线false与平面false所成的角,
设false,又false
所以falsefalse
故false
故选:A
【点睛】
方法点晴:求线面夹角一般有两种方法:
(1)几何法:作平面的垂线,找到夹角再用三角函数求解;
(2)向量法:建系用空间向量公式求解.
6.D
【分析】
连接false,证得平面false平面false,可判定A正确;根据false,可判定B正确;当点false为线段false的中点时,求得线段false的长度最小值,可判定C正确;求得false与平面false所成角的正切值的取值范围,可判定D错误.
【详解】
连接false,由false且false,
可得四边形false为平行四边形,所以false,
又由false平面false,且false平面false,所以false平面false,
同理可得false平面false,又false,可得平面false平面false,
所以对于任意点false,则false平面false,所以A正确;
由false,所以B正确;
当点false为线段false的中点时,可得false,
此时线段false的长度最小,最小值为false,所以C正确;
当点false在线段false上运动时,false长度的最小值为false,最大值为false,
又由false长度的取值范围为false,而点false到平面false的距离为定值1,
因为平面false平面false,
所以false与平面false所成角与false与平面false所成角相等,
又由false平面false,可得false在平面false射影为false,
所以false在平面false所成角的正切值为false,
即false与平面false所成角的正切值的取值范围为false,
其最大值小于false,则不存在点false使得false与平面false所成角的大小为false,
所以D错误.
故选:D.
【点睛】
1、对面面平行判定定理的条件“面内两相交直线”认识不清导致错解;
2、等体积法:等体积法也称积转化或等积变形,通过选择合适的底面来求几何体体积的一种方法,多用来解决锥体的体积,特别时三棱锥的体积.
3、求解直线与平面所成角时,根据直线与平面所成角的定义,结合垂线段与斜线段的长度比求得线面角的正弦值.
7.D
【分析】
由中位线性质,平移异面直线即可判断MN不与AB平行,根据异面直线平面角知MN与BC所成的角为90°,应用反证知OC不与平面VAC垂直,由面面垂直的判定知面VACfalse面VBC,即可知正确选项.
【详解】
M,N分别为VA,VC的中点,在△false中有false,
在面false中false,MN不与AB平行;
false,知:MN与BC所成的角为false;
因为false面false,false与平面内交线false都不垂直,OC不与平面VAC垂直;
由false面false,false面false即false,而false知false,false有falsefalse面false,又false面false,所以面falsefalse面false;
故选:D
【点睛】
本题考查了异面直线的位置关系、夹角,以及线面垂直的性质,面面垂直判定的应用,属于基础题.
8.C
【分析】
①由平面false平行平面false判断;②由四边形false为矩形,false变化而false不变判断;③由false始终与EH平行判断;④由水的体积是定值,高不变,底面面积不变判断.
【详解】
①由棱柱的特征知:平面false平行平面false,故正确;
②因为四边形false是矩形,false的长度变化,false长度不变,所以面积是改变的,故错误;
③因为false,false平面EFGH,false平面EFGH,所以false平面EFGH,故正确;
④因为水的体积是定值,高不变,所以底面面积不变,所以false时,false是定值.故正确.
故选:C.
9.AD
【分析】
利用线面垂直的判定,线面平行的判定,线线的位置关系及面面平行的性质逐一判断即可.
【详解】
由m,n是两条不同的直线,α,β是两个不同的平面,得:
对于A,若m⊥α,n⊥α,则由线面垂直的性质定理得m∥n,故A正确;
对于B,若m∥n,m∥α,则n∥α或n?α,故B错误;
对于C,若m?α,n?β,则m,n相交、平行或异面,故C错误;
对于D,若α∥β,m?α,n?β,则m∥n或m,n是异面直线,故D正确.
故选:AD.
【点睛】
本题主要考查了线面垂直的性质,线面平行的判定和面面平行的性质.
10.BC
【分析】
由题意可得,AH⊥HE,AH⊥HF,HF⊥HE,从而利用线面垂直的判定定理可得AH⊥平面EFH,HF⊥平面AHE,进而可得答案
【详解】
解:由题意可得:AH⊥HE,AH⊥HF.
∴AH⊥平面EFH,而AG与平面EFH不垂直.∴B正确,A不正确.
又HF⊥HE,∴HF⊥平面AHE,C正确.
HG与AG不垂直,因此HG⊥平面AEF不正确.D不正确.
故选:BC.
【点睛】
此题考查线面垂直的判定,考查折叠问题,属于基础题
11.false
【分析】
对平面的位置关系分类讨论,即可得到答案.
【详解】
当三个不同的平面互相平行时,最少将空间分成4部分,即false,
当三个平面三维放置时,最多将空间分成8部分,即false,
所以false.
故答案为:false
【点睛】
方法点睛:对平面分空间为几个部分问题,要有画图的意识,结合空间想象能力全方位、多角度地去考虑问题,作出判断.
12.对角线垂直(底面是菱形、正方形皆可).
【解析】
试题分析::∵四棱柱ABCD -A1B1C1D1是直棱柱,∴false,若false,
则false⊥平面false,∴false⊥AC,又由false∥BD,则有BD⊥AC,
反之,由BD⊥AC亦可得到false
考点:空间中直线与直线之间的位置关系
13.平行
【分析】
利用线面平行的判定定理和线面平行的性质定理,即可判断出false与直线false平行.
【详解】
在三棱柱false中,false,false平面false,false平面false,
所以false平面false,又因为false平面false,且平面false平面false,
所以false.
故答案为:平行
14.45°
【分析】
由线面垂直找出AM在面ABC内射影得线面角,在△PCM中计算而得.
【详解】
∵PC⊥AC,PC⊥BC,AC∩BC=C,∴PC⊥平面ABC,
∴PM在平面ABC内的射影为CM,故∠PMC为PM与平面ABC所成的角.
∵AC=BC=5false,∠ACB=90°,而AB的中点为M,
∴CM=5,又PC=5,∴△PCM为等腰直角三角形,
∴∠PMC=45°,即PM与平面ABC所成的角为45°.
故答案为:45°
15.(Ⅰ)∵点E、F是线段AC、BC的中点,∴EF∥AB,
又∵G、H是线段BD、AD的中点,∴GH∥AB,
∴EF∥GH, 因此: E、F、G、H四点共面;
(Ⅱ)∵平面false//平面false,点A、B在平面false内,∴AB//平面false
设平面ABC与平面false的交线为CP,
∵直线AB与CD是异面直线, ∴CP与CD是交线,
∵AB//平面false, ∴AB//CP, 又EF∥AB, ∴EF//CP,∴EF∥平面false,
∵点E、H是线段AC、AD的中点,∴EH∥CD, ∴EH∥平面false,
因此:平面EFGH//平面false
【解析】
考点:平面与平面平行的判定.
分析:(Ⅰ)根据中位线定理可知EF∥AB,GH∥AB,从而EF∥GH,根据公理可知两平行线确定一平面,则E、F、G、H四点共面;
(Ⅱ)根据平面α∥平面β,点A、B在平面α内,则AB∥平面α,设平面ABC与平面β的交线为CP,根据AB∥平面α,则AB∥CP,又EF∥AB,则EF∥CP,根据线面平行的判定定理可知EF∥平面β,根据中位线定理可知EH∥CD,从而EH∥平面β,最后根据面面平行的判定定理可平面EFGH∥平面β.
解答:证:(Ⅰ)∵点E、F是线段AC、BC的中点,
∴EF∥AB,
又∵G、H是线段BD、AD的中点,∴GH∥AB,
∴EF∥GH,因此:E、F、G、H四点共面;
(Ⅱ)∵平面α∥平面β,点A、B在平面α内,∴AB∥平面α
设平面ABC与平面β的交线为CP,
∵直线AB与CD是异面直线,
∴CP与CD是交线,
∵AB∥平面α,∴AB∥CP,又EF∥AB,
∴EF∥CP,∴EF∥平面β,
∵点E、H是线段AC、AD的中点,
∴EH∥CD,∴EH∥平面β,
因此:平面EFGH∥平面β.
点评:本题考查证明两个平面平行的方法:在一个平面内找到两条条相交的直线和另一个平面平行,属于基础题.
16.(1)证明见解析;(2)false
【分析】
(1)通过AC⊥BD与PD⊥AC可得false平面false;
(2)由题先得出∠PBD是直线PB与平面ABCD所成的角,即∠PBD=45°,则可先求出菱形ABCD的面积,进而可得四棱锥P- ABCD的体积.
【详解】
解:(1)因为四边形ABCD是菱形,所以AC⊥BD,
又因为PD⊥平面ABCD,false平面ABCD,
所以PD⊥AC,又false,
故AC⊥平面PBD;
(2)因为PD⊥平面ABCD,
所以∠PBD是直线PB与平面ABCD所成的角,
于是∠PBD=45°,
因此BD=PD=2.又AB= AD=2,
所以菱形ABCD的面积为false,
故四棱锥P- ABCD的体积false.
17.(1)证明见解析;(2)证明见解析.
【分析】
( 1)设false与false的交点为false,连接false,通过直线与平面平行的判定定理证明false平面false;
( 2)通过体积得到底面为正方形,再由线面垂直得到面面垂直即可.
【详解】
(1)连接false交false于点O,连结false,
因为false为矩形,所以O为false的中点,
又E为false的中点,所以false,
false平面false,false平面false,所以false平面false.
(2)因为false,
所以false,所以底面false为正方形,所以false,
因为false,所以false,且false,所以false平面false,
又false平面false,所以平面false平面false.
【点睛】
本题主要考查了立体几何及其运算,要证明线面平行先证明线线平行,要证明面面垂直,先证明线面垂直,考查了学生的基础知识、空间想象力.
同课章节目录
