福建省福州市平潭县新世纪学校2021届高三下学期5月百盛冲刺班数学测试(10) Word版含答案
文档属性
| 名称 | 福建省福州市平潭县新世纪学校2021届高三下学期5月百盛冲刺班数学测试(10) Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 393.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 09:40:44 | ||
图片预览




文档简介
平潭县新世纪学校百盛高三冲刺班数学测试(十)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知x,y∈R,集合A={1,2x},B={x,y},A∩B=,则xy=( )
A.-1 B.- C. D.1
2.在复数范围内,实系数一元二次方程一定有根,已知方程x2+ax+b=0(a∈R,b∈R)的一个根为1+i(i为虚数单位),则=( )A.1-i B.-1+i C.2i D.2+i
5057775330203.在△ABC中,已知A=45°,AB=6,且AB边上的高为2,则sin C=( )A. B. C. D.
4.设m,n为非零向量,则“存在正数λ,使得m=λn”是“m·n>0”的( )
A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
5433695247655.如图,标准对数远视力表采用的“五分记录法”是我国独创的视力记录方式,标准对数远视力表各行为正方形“E”形视标,且从视力5.2的视标所在行开始往上,每一行“E”的边长都是下方一行“E”的边长的倍,若视力4.0的视标边长为a,则视力4.8的视标边长为( )A.a B.a C. D.
6.已知△ABC是边长为4的等边三角形,D为 AB的中点,以CD为折痕,将△ABC折成直二面角A-CD-B,则过A,B,C,D四点的球的表面积为( )
A.18π B.20π C.22π D.24π
7.函数f(x)=(-π≤x≤π)的图象大致为( )
A B C D
8.已知函数f(x)=(x-1)ex-e2x+ax只有一个极值点,则实数a的取值范围是( )
A. B. C.{a|a≤0} D.
二、多选题
9.(多选)下列结论正确的有( )
A.若随机变量ξ~N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=0.21
B.若X~B,则D(3X+2)=22
C.已知回归直线方程为y=x+10.8,且=4,=50,则=9.8
D.已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数、中位数、众数依次成等差数列,则丢失数据的所有可能值的和为22
10.(多选)将函数y=2cos x+1的图象上各点的横坐标缩短到原来的,纵坐标不变,再向左平移个单位长度,得到f(x)的图象,下列说法正确的是( )
A.点是函数f(x)图象的对称中心 B.函数f(x)在上单调递减
C.函数f(x)的图象与函数g(x)=2sin+1的图象相同
D.若x1,x2是函数f(x)的零点,则x1-x2是π的整数倍
11.(多选)已知函数f(x)=若x1 510032054610012.(多选)如图,点M是正方体ABCD-A1B1C1D1中的侧面ADD1A1上(包含边界)的一个动点,则下列结论正确的是( )
A.点M存在无数个位置满足CM⊥AD1
B.若正方体的棱长为1,三棱锥B-C1MD的体积最大值为
C.在线段AD1上存在点M,使异面直线B1M与CD所成角是30°
D.点M存在无数个位置满足到直线AD和直线C1D1的距离相等
三、填空题
13.直线y=x被圆(x-2)2+y2=4截得的弦长为__________.
14.二项式9的展开式中,除常数项外,各项系数的和为__________.
15.已知双曲线C:-=1(a>0,b>0)的左、右焦点和点P(2a,b)为某个等腰三角形的三个顶点,则双曲线C的离心率为__________.
16.我们称一个数列是“有趣数列”,当且仅当该数列满足以下两个条件:
①所有的奇数项满足a2n-1 ②任意相邻的两项a2n-1,a2n满足a2n-1 若an=n+(-1)n,则数列{an}__________“有趣数列”(填“是”或“不是”).
一、解答题
1.在①false,②false,③false这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求false的值;若问题中的三角形不存在,说明理由.
问题:是否存在false,它的内角false的对边分别为false,且false,false,________?
注:如果选择多个条件分别解答,按第一个解答计分.
2.等比数列false的各项均为正数,且false.
(1)求数列false的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列false的前false项和false.
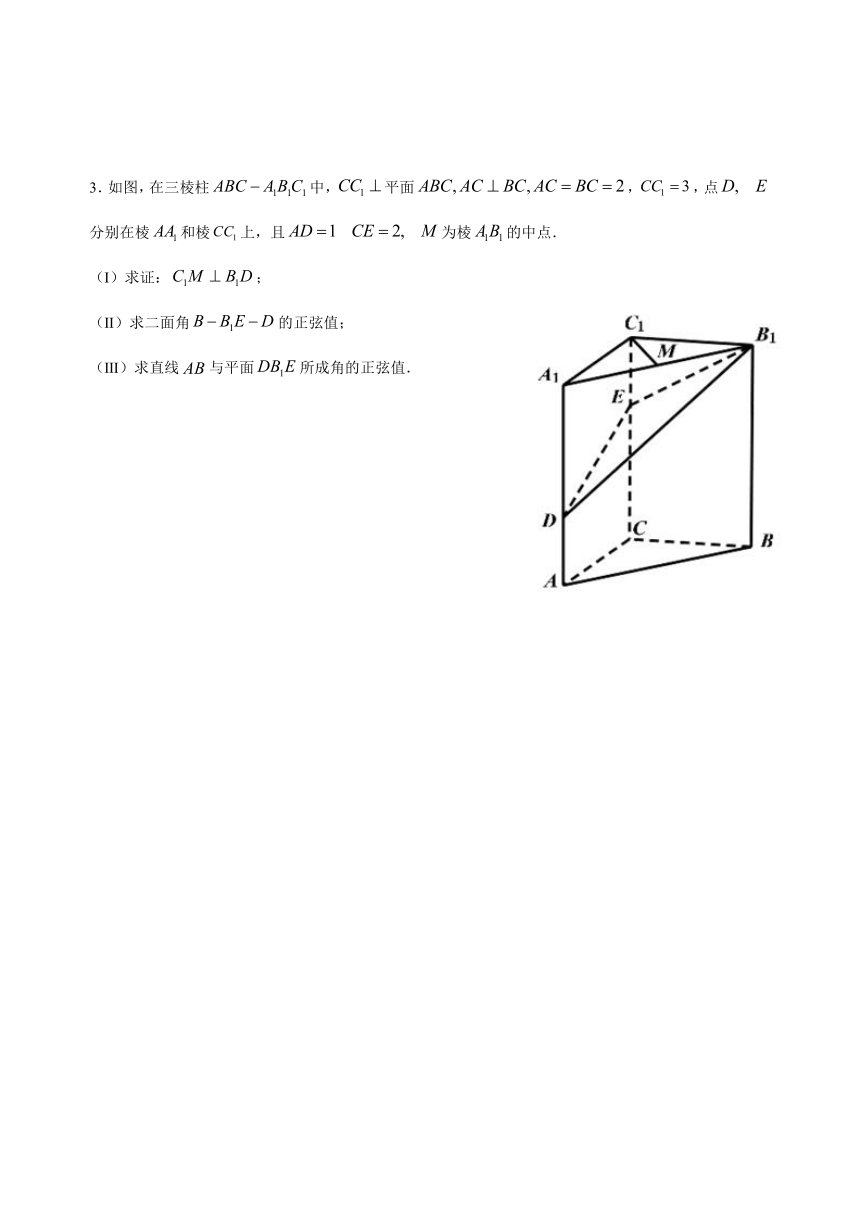
3.如图,在三棱柱false中,false平面false,false,点false分别在棱false和棱false上,且false为棱false的中点.
3790950375285(Ⅰ)求证:false;
(Ⅱ)求二面角false的正弦值;
(Ⅲ)求直线false与平面false所成角的正弦值.
参考答案
1. B
解析 因为A∩B=,所以2x=,即x=-1,所以y=,故xy=-.故选B项.
2.B
解析 因为x1=1+i是关于x的实系数一元二次方程x2+ax+b=0的一个根,所以x2=1-i也是此方程的一个虚根,所以a=-(x1+x2)=-(1+i+1-i)=-2.所以===-1+i.故选B项.
3.答案 B
解析 如图,在△ABC中,A=45°,AB=6,且AB边上的高CD为2,所以AD=CD=2,AC==4,所以由余弦定理可得BC2=AC2+AB2-2AC·AB·cos A=16+72-2×4×6×=40,即BC=,所以由正弦定理=,可以得到sin ∠ACB===.故选B项.
4.答案 A
解析 由题意,存在正数λ,使得m=λn,所以m,n同向,所以m·n=|m||n|cos〈m,n〉>0,即充分性是成立的.反之,当非零向量m,n的夹角为锐角时,满足m·n>0,而此时 m=λn不成立,即必要性不成立.所以“存在正数λ,使得m=λn”是“m·n>0”的充分不必要条件.故选A项.
5.答案 C
解析 设第n行视标边长为an,第n-1行视标边长为an-1,则a1=A.由题意可得an-1=an,所以=,所以数列{an}是首项为a,公比为的等比数列,即,所以视力4.8的视标边长为.故选C项.
6.答案 B
解析 如图所示,由题意可得在△ABC中,CD⊥AB,所以在直二面角A-CD-B中,BD⊥CD,AD⊥CD.所以∠ADB为直二面角A-CD-B的平面角,即∠ADB=90°.
设三棱锥B-ACD的外接球的半径为R,可得(2R)2=AD2+BD2+CD2=22+22+(2)2,所以4R2=20.所以过A,B,C,D四点的球的表面积S=4πR2=20π.故选B项.
7.答案 A
解析 由函数的解析式可得f(-x)=-f(x),所以函数f(x)的图象关于坐标原点对称,排除B项;设函数g(x)=ex+e-x,则g′(x)=ex-e-x=,当x>0时,g′(x)>0,所以g(x)单调递增,则g0,sin x>0,则f(x)>0,排除D项.故选A项.
8.答案 A
解析 f(x)=(x-1)ex-e2x+ax,则f′(x)=xex-ae2x+a,当a=0时,f′(x)=xex,易知函数f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,且f′(0)=0,故函数有唯一极小值点,满足条件;当a≠0时,令f′(x)=0,则x-aex+=0,即=ex-e-x,设g(x)=ex-e-x,则g′(x)=ex+e-x≥2恒成立,且g′(0)=2,画出函数g(x)和y=的图象,如图所示.
根据图象知,当≤2,即a<0或a≥时,满足条件.综上所述,实数a的取值范围是.故选A项.
9.答案 AC
解析 因为随机变量ξ~N(1,σ2),P(ξ≤4)=0.79,所以P(ξ≤-2)=1-P(ξ≤4)=0.21,A项正确;因为X~B,所以D(X)=10××=,故D(3X+2)=9D(X)=20,B项错误;将(,)代入回归直线方程,计算得到 =9.8,C项正确;设丢失的数据为x,则平均数为,众数为3,当x≤3时,中位数为3,则3×2=+3,所以x=-10,当3 10.答案 BC
解析 将函数y=2cos x+1的图象上各点的横坐标缩短到原来的,纵坐标不变,可得到函数y=2cos 2x+1的图象,再向左平移个单位长度,可得到函数f(x)=2cos+1的图象.对于A项,令x=,求得f(x)=1,故A项错误;对于B项,若x∈,则2x+∈,故f(x)=2cos+1在上单调递减,故B项正确;对于C项, f(x)=2cos+1=2cos+1=2sin+1=g(x),即函数f(x)的图象与函数g(x)的图象相同,故C项正确;对于D项,可取函数f(x)的零点x1=,x2=,此时x1-x2不是π的整数倍,故D项错误.故选BC项.
11.答案 BCD
解析 画出函数f(x)的大致图象如图所示.
所以x1+x2=-2,-log2x3=log2x4,则x3x4=1,故A项错误,B项正确;由图可知1 12.答案 ABD
解析 A项,如图①,连接AD1,A1D,MC,A1C,由正方体的性质可得AD1⊥A1D,AD1⊥DC,又A1D∩DC=D,所以AD1⊥平面A1DC,当点M∈A1D时,有CM?平面A1DC,所以CM⊥AD1,故点M存在无数个位置满足 CM⊥AD1,故A项正确;
图① 图②
B项,如图②,由已知VB-C1MD=VM-C1BD,当点M与点A1重合时,点M到平面C1BD的距离最大,则三棱锥 B-C1MD的体积最大值VA-C1BD=13-4×××1×1×1=,故B项正确;C项,如图③,连接A1M,因为CD∥A1B1,所以∠A1B1M为异面直线B1M与CD所成的角.设正方体棱长为1,A1M=x,则B1M2=x2+1,因为点A1到线段AD1的距离为==,所以≤x≤1,若在线段AD1上存在点M使异面直线B1M与CD所成的角是30°,则cos∠A1B1M==cos30°=,解得x=?,所以在线段AD1上不存在点M,使异面直线B1M与CD所成的角是30°,故C项错误;
图③ 图④
D项,如图④,连接MD1,过M作MN⊥AD交AD于N,则线段MN为点M到直线AD的距离,由C1D1⊥平面ADD1A1,MD1?平面ADD1A1,得MD1⊥D1C1,则MD1为点M到直线C1D1的距离,要使MD1=MN,只需点M在以D1为焦点,以AD为准线的抛物线上,故这样的点M有无数个,故D项正确.故选ABD项.
13.解析 直线方程一般式为x-y=0,圆心为(2,0),它到已知直线的距离d==1,圆半径为r=2,所以弦长为2=2×=2.
答案 2
14.解析 令x=1,可得该二项式各项系数的和为-1.因为该二项展开式的通项公式为Tr+1=C·9-r·(-2x2)r=C(-2)r·x3r-9,令3r-9=0,得r=3,所以该二项展开式中的常数项为C(-2)3=-672,所以除常数项外,各项系数的和为-1-(-672)=671.
答案 671
15.解析 设双曲线C的左、右焦点分别为F1(-c,0),F2(c,0),离心率为e.因为左、右焦点和点P(2a,b)为某个等腰三角形的三个顶点,故当F1F2=PF2时,2c=,由b2=c2-a2可得2c2+4ac-3a2=0,等式两边同除以a2可得2e2+4e-3=0,解得e=<1(舍);当F1F2=PF1时,2c=,由b2=c2-a2可得2c2-4ac-3a2=0,等式两边同除以a2可得2e2-4e-3=0,解得e=;当PF1=PF2时,显然不存在.综上,双曲线C的离心率为.
答案
16解析 若an=n+(-1)n,则a2n-1=2n-1-,a2n+1=2n+1-,a2n=2n+,a2n+2=2n+2+.于是a2n-1-a2n+1=-2-+=-2-<0,故a2n-1 答案 是
16.详见解析
【分析】
解法一:由题意结合所给的条件,利用正弦定理角化边,得到a,b的比例关系,根据比例关系,设出长度长度,由余弦定理得到false的长度,根据选择的条件进行分析判断和求解.
解法二:利用诱导公式和两角和的三角函数公式求得false的值,得到角false的值,然后根据选择的条件进行分析判断和求解.
【详解】
解法一:
由false可得:false,
不妨设false,
则:false,即false.
选择条件①的解析:
据此可得:false,false,此时false.
选择条件②的解析:
据此可得:false,
则:false,此时:false,则:false.
选择条件③的解析:
可得false,false,
与条件false矛盾,则问题中的三角形不存在.
解法二:∵false,
∴false,
false ,
∴false,∴false,∴false,∴false,
若选①,false,∵false,∴false,∴c=1;
若选②,false,则false,false;
若选③,与条件false矛盾.
【点睛】
在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.
17.(1)false;(2)false.
【分析】
(1)根据题意列出方程组,求出首项与公比,即可求出等比数列的通项公式即可;
(2)由an=false化简bn=log3a1+log3a2+…+log3an,可得到bn的通项公式,求出false的通项公式,利用裂项相消法求和.
【详解】
(1)设数列{an}的公比为q,
由false=9a2a6得false=9false,
所以q2=false.由条件可知q>0,故q=false.
由2a1+3a2=1得2a1+3a1q=1,所以a1=false.
故数列{an}的通项公式为an=false.
(2)bn=log3a1+log3a2+…+log3an=-(1+2+…+n)=-false.
故false.
false
所以数列false的前n项和为false
18.(Ⅰ)证明见解析;(Ⅱ)false;(Ⅲ)false.
【分析】
以false为原点,分别以false的方向为false轴,false轴,false轴的正方向建立空间直角坐标系.
(Ⅰ)计算出向量false和false的坐标,得出false,即可证明出false;
(Ⅱ)可知平面false的一个法向量为false,计算出平面false的一个法向量为false,利用空间向量法计算出二面角false的余弦值,利用同角三角函数的基本关系可求解结果;
(Ⅲ)利用空间向量法可求得直线false与平面false所成角的正弦值.
【详解】
依题意,以false为原点,分别以false、false、false的方向为false轴、false轴、false轴的正方向建立空间直角坐标系(如图),
可得false、false、false、false、
false、false、false、false、false.
(Ⅰ)依题意,false,false,
从而false,所以false;
(Ⅱ)依题意,false是平面false的一个法向量,
false,false.
设false为平面false的法向量,
则false,即false,
不妨设false,可得false.
false,
false.
所以,二面角false的正弦值为false;
(Ⅲ)依题意,false.
由(Ⅱ)知false为平面false的一个法向量,于是false.
所以,直线false与平面false所成角的正弦值为false.
【点睛】
本题考查利用空间向量法证明线线垂直,求二面角和线面角的正弦值,考查推理能力与计算能力,属于中档题.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知x,y∈R,集合A={1,2x},B={x,y},A∩B=,则xy=( )
A.-1 B.- C. D.1
2.在复数范围内,实系数一元二次方程一定有根,已知方程x2+ax+b=0(a∈R,b∈R)的一个根为1+i(i为虚数单位),则=( )A.1-i B.-1+i C.2i D.2+i
5057775330203.在△ABC中,已知A=45°,AB=6,且AB边上的高为2,则sin C=( )A. B. C. D.
4.设m,n为非零向量,则“存在正数λ,使得m=λn”是“m·n>0”的( )
A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
5433695247655.如图,标准对数远视力表采用的“五分记录法”是我国独创的视力记录方式,标准对数远视力表各行为正方形“E”形视标,且从视力5.2的视标所在行开始往上,每一行“E”的边长都是下方一行“E”的边长的倍,若视力4.0的视标边长为a,则视力4.8的视标边长为( )A.a B.a C. D.
6.已知△ABC是边长为4的等边三角形,D为 AB的中点,以CD为折痕,将△ABC折成直二面角A-CD-B,则过A,B,C,D四点的球的表面积为( )
A.18π B.20π C.22π D.24π
7.函数f(x)=(-π≤x≤π)的图象大致为( )
A B C D
8.已知函数f(x)=(x-1)ex-e2x+ax只有一个极值点,则实数a的取值范围是( )
A. B. C.{a|a≤0} D.
二、多选题
9.(多选)下列结论正确的有( )
A.若随机变量ξ~N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=0.21
B.若X~B,则D(3X+2)=22
C.已知回归直线方程为y=x+10.8,且=4,=50,则=9.8
D.已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数、中位数、众数依次成等差数列,则丢失数据的所有可能值的和为22
10.(多选)将函数y=2cos x+1的图象上各点的横坐标缩短到原来的,纵坐标不变,再向左平移个单位长度,得到f(x)的图象,下列说法正确的是( )
A.点是函数f(x)图象的对称中心 B.函数f(x)在上单调递减
C.函数f(x)的图象与函数g(x)=2sin+1的图象相同
D.若x1,x2是函数f(x)的零点,则x1-x2是π的整数倍
11.(多选)已知函数f(x)=若x1
A.点M存在无数个位置满足CM⊥AD1
B.若正方体的棱长为1,三棱锥B-C1MD的体积最大值为
C.在线段AD1上存在点M,使异面直线B1M与CD所成角是30°
D.点M存在无数个位置满足到直线AD和直线C1D1的距离相等
三、填空题
13.直线y=x被圆(x-2)2+y2=4截得的弦长为__________.
14.二项式9的展开式中,除常数项外,各项系数的和为__________.
15.已知双曲线C:-=1(a>0,b>0)的左、右焦点和点P(2a,b)为某个等腰三角形的三个顶点,则双曲线C的离心率为__________.
16.我们称一个数列是“有趣数列”,当且仅当该数列满足以下两个条件:
①所有的奇数项满足a2n-1
一、解答题
1.在①false,②false,③false这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求false的值;若问题中的三角形不存在,说明理由.
问题:是否存在false,它的内角false的对边分别为false,且false,false,________?
注:如果选择多个条件分别解答,按第一个解答计分.
2.等比数列false的各项均为正数,且false.
(1)求数列false的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列false的前false项和false.
3.如图,在三棱柱false中,false平面false,false,点false分别在棱false和棱false上,且false为棱false的中点.
3790950375285(Ⅰ)求证:false;
(Ⅱ)求二面角false的正弦值;
(Ⅲ)求直线false与平面false所成角的正弦值.
参考答案
1. B
解析 因为A∩B=,所以2x=,即x=-1,所以y=,故xy=-.故选B项.
2.B
解析 因为x1=1+i是关于x的实系数一元二次方程x2+ax+b=0的一个根,所以x2=1-i也是此方程的一个虚根,所以a=-(x1+x2)=-(1+i+1-i)=-2.所以===-1+i.故选B项.
3.答案 B
解析 如图,在△ABC中,A=45°,AB=6,且AB边上的高CD为2,所以AD=CD=2,AC==4,所以由余弦定理可得BC2=AC2+AB2-2AC·AB·cos A=16+72-2×4×6×=40,即BC=,所以由正弦定理=,可以得到sin ∠ACB===.故选B项.
4.答案 A
解析 由题意,存在正数λ,使得m=λn,所以m,n同向,所以m·n=|m||n|cos〈m,n〉>0,即充分性是成立的.反之,当非零向量m,n的夹角为锐角时,满足m·n>0,而此时 m=λn不成立,即必要性不成立.所以“存在正数λ,使得m=λn”是“m·n>0”的充分不必要条件.故选A项.
5.答案 C
解析 设第n行视标边长为an,第n-1行视标边长为an-1,则a1=A.由题意可得an-1=an,所以=,所以数列{an}是首项为a,公比为的等比数列,即,所以视力4.8的视标边长为.故选C项.
6.答案 B
解析 如图所示,由题意可得在△ABC中,CD⊥AB,所以在直二面角A-CD-B中,BD⊥CD,AD⊥CD.所以∠ADB为直二面角A-CD-B的平面角,即∠ADB=90°.
设三棱锥B-ACD的外接球的半径为R,可得(2R)2=AD2+BD2+CD2=22+22+(2)2,所以4R2=20.所以过A,B,C,D四点的球的表面积S=4πR2=20π.故选B项.
7.答案 A
解析 由函数的解析式可得f(-x)=-f(x),所以函数f(x)的图象关于坐标原点对称,排除B项;设函数g(x)=ex+e-x,则g′(x)=ex-e-x=,当x>0时,g′(x)>0,所以g(x)单调递增,则g
8.答案 A
解析 f(x)=(x-1)ex-e2x+ax,则f′(x)=xex-ae2x+a,当a=0时,f′(x)=xex,易知函数f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,且f′(0)=0,故函数有唯一极小值点,满足条件;当a≠0时,令f′(x)=0,则x-aex+=0,即=ex-e-x,设g(x)=ex-e-x,则g′(x)=ex+e-x≥2恒成立,且g′(0)=2,画出函数g(x)和y=的图象,如图所示.
根据图象知,当≤2,即a<0或a≥时,满足条件.综上所述,实数a的取值范围是.故选A项.
9.答案 AC
解析 因为随机变量ξ~N(1,σ2),P(ξ≤4)=0.79,所以P(ξ≤-2)=1-P(ξ≤4)=0.21,A项正确;因为X~B,所以D(X)=10××=,故D(3X+2)=9D(X)=20,B项错误;将(,)代入回归直线方程,计算得到 =9.8,C项正确;设丢失的数据为x,则平均数为,众数为3,当x≤3时,中位数为3,则3×2=+3,所以x=-10,当3
解析 将函数y=2cos x+1的图象上各点的横坐标缩短到原来的,纵坐标不变,可得到函数y=2cos 2x+1的图象,再向左平移个单位长度,可得到函数f(x)=2cos+1的图象.对于A项,令x=,求得f(x)=1,故A项错误;对于B项,若x∈,则2x+∈,故f(x)=2cos+1在上单调递减,故B项正确;对于C项, f(x)=2cos+1=2cos+1=2sin+1=g(x),即函数f(x)的图象与函数g(x)的图象相同,故C项正确;对于D项,可取函数f(x)的零点x1=,x2=,此时x1-x2不是π的整数倍,故D项错误.故选BC项.
11.答案 BCD
解析 画出函数f(x)的大致图象如图所示.
所以x1+x2=-2,-log2x3=log2x4,则x3x4=1,故A项错误,B项正确;由图可知1
解析 A项,如图①,连接AD1,A1D,MC,A1C,由正方体的性质可得AD1⊥A1D,AD1⊥DC,又A1D∩DC=D,所以AD1⊥平面A1DC,当点M∈A1D时,有CM?平面A1DC,所以CM⊥AD1,故点M存在无数个位置满足 CM⊥AD1,故A项正确;
图① 图②
B项,如图②,由已知VB-C1MD=VM-C1BD,当点M与点A1重合时,点M到平面C1BD的距离最大,则三棱锥 B-C1MD的体积最大值VA-C1BD=13-4×××1×1×1=,故B项正确;C项,如图③,连接A1M,因为CD∥A1B1,所以∠A1B1M为异面直线B1M与CD所成的角.设正方体棱长为1,A1M=x,则B1M2=x2+1,因为点A1到线段AD1的距离为==,所以≤x≤1,若在线段AD1上存在点M使异面直线B1M与CD所成的角是30°,则cos∠A1B1M==cos30°=,解得x=?,所以在线段AD1上不存在点M,使异面直线B1M与CD所成的角是30°,故C项错误;
图③ 图④
D项,如图④,连接MD1,过M作MN⊥AD交AD于N,则线段MN为点M到直线AD的距离,由C1D1⊥平面ADD1A1,MD1?平面ADD1A1,得MD1⊥D1C1,则MD1为点M到直线C1D1的距离,要使MD1=MN,只需点M在以D1为焦点,以AD为准线的抛物线上,故这样的点M有无数个,故D项正确.故选ABD项.
13.解析 直线方程一般式为x-y=0,圆心为(2,0),它到已知直线的距离d==1,圆半径为r=2,所以弦长为2=2×=2.
答案 2
14.解析 令x=1,可得该二项式各项系数的和为-1.因为该二项展开式的通项公式为Tr+1=C·9-r·(-2x2)r=C(-2)r·x3r-9,令3r-9=0,得r=3,所以该二项展开式中的常数项为C(-2)3=-672,所以除常数项外,各项系数的和为-1-(-672)=671.
答案 671
15.解析 设双曲线C的左、右焦点分别为F1(-c,0),F2(c,0),离心率为e.因为左、右焦点和点P(2a,b)为某个等腰三角形的三个顶点,故当F1F2=PF2时,2c=,由b2=c2-a2可得2c2+4ac-3a2=0,等式两边同除以a2可得2e2+4e-3=0,解得e=<1(舍);当F1F2=PF1时,2c=,由b2=c2-a2可得2c2-4ac-3a2=0,等式两边同除以a2可得2e2-4e-3=0,解得e=;当PF1=PF2时,显然不存在.综上,双曲线C的离心率为.
答案
16解析 若an=n+(-1)n,则a2n-1=2n-1-,a2n+1=2n+1-,a2n=2n+,a2n+2=2n+2+.于是a2n-1-a2n+1=-2-+=-2-<0,故a2n-1
16.详见解析
【分析】
解法一:由题意结合所给的条件,利用正弦定理角化边,得到a,b的比例关系,根据比例关系,设出长度长度,由余弦定理得到false的长度,根据选择的条件进行分析判断和求解.
解法二:利用诱导公式和两角和的三角函数公式求得false的值,得到角false的值,然后根据选择的条件进行分析判断和求解.
【详解】
解法一:
由false可得:false,
不妨设false,
则:false,即false.
选择条件①的解析:
据此可得:false,false,此时false.
选择条件②的解析:
据此可得:false,
则:false,此时:false,则:false.
选择条件③的解析:
可得false,false,
与条件false矛盾,则问题中的三角形不存在.
解法二:∵false,
∴false,
false ,
∴false,∴false,∴false,∴false,
若选①,false,∵false,∴false,∴c=1;
若选②,false,则false,false;
若选③,与条件false矛盾.
【点睛】
在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.
17.(1)false;(2)false.
【分析】
(1)根据题意列出方程组,求出首项与公比,即可求出等比数列的通项公式即可;
(2)由an=false化简bn=log3a1+log3a2+…+log3an,可得到bn的通项公式,求出false的通项公式,利用裂项相消法求和.
【详解】
(1)设数列{an}的公比为q,
由false=9a2a6得false=9false,
所以q2=false.由条件可知q>0,故q=false.
由2a1+3a2=1得2a1+3a1q=1,所以a1=false.
故数列{an}的通项公式为an=false.
(2)bn=log3a1+log3a2+…+log3an=-(1+2+…+n)=-false.
故false.
false
所以数列false的前n项和为false
18.(Ⅰ)证明见解析;(Ⅱ)false;(Ⅲ)false.
【分析】
以false为原点,分别以false的方向为false轴,false轴,false轴的正方向建立空间直角坐标系.
(Ⅰ)计算出向量false和false的坐标,得出false,即可证明出false;
(Ⅱ)可知平面false的一个法向量为false,计算出平面false的一个法向量为false,利用空间向量法计算出二面角false的余弦值,利用同角三角函数的基本关系可求解结果;
(Ⅲ)利用空间向量法可求得直线false与平面false所成角的正弦值.
【详解】
依题意,以false为原点,分别以false、false、false的方向为false轴、false轴、false轴的正方向建立空间直角坐标系(如图),
可得false、false、false、false、
false、false、false、false、false.
(Ⅰ)依题意,false,false,
从而false,所以false;
(Ⅱ)依题意,false是平面false的一个法向量,
false,false.
设false为平面false的法向量,
则false,即false,
不妨设false,可得false.
false,
false.
所以,二面角false的正弦值为false;
(Ⅲ)依题意,false.
由(Ⅱ)知false为平面false的一个法向量,于是false.
所以,直线false与平面false所成角的正弦值为false.
【点睛】
本题考查利用空间向量法证明线线垂直,求二面角和线面角的正弦值,考查推理能力与计算能力,属于中档题.
同课章节目录
