广东省珠海第二高级中学校2021届高三下学期5月数学测试卷(5月11日) Word版含答案
文档属性
| 名称 | 广东省珠海第二高级中学校2021届高三下学期5月数学测试卷(5月11日) Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 09:44:06 | ||
图片预览



文档简介
珠海市第二中学高三数学测试(5月11日)
一.选择题(共8小题)
1.已知false,false是false的子集,且false,则false false
A.false
B.false
C.false
D.false
2.已知复数false为虚部单位),则false的最大值为false false
A.1
B.false
C.2
D.3
3.双曲线false的虚轴长是实轴长的2倍,则实数false的值是false false
A.16
B.false
C.false
D.false
4.设false,false,false,则false false
A.false
B.false
C.false
D.false
5.已知离散型随机变量false,false的分布列为
false
1
3
5
false
false
false
false
false
1
2
4
5
false
false
false
false
false
则下列说法一定正确的是false false
A.false
B.false
C.false
D.false
6.已知数列false,false均为等差数列,若false,false,false则false false
A.19
B.21
C.23
D.27
7.若指数函数false与函数false的图象恰有三个不同的交点,则实数false的取值范围是false false
A.false
B.false
C.false
D.false
8.甲、乙、丙三位同学参加学习脱贫干部黄文秀、戍边英雄陈红军、人民科学家南仁东、抗疫英雄张定宇等英雄的先进事迹知识竞赛.该竞赛共有十道判断题,三位同学的答题情况如下:考试成绩公布后,三个人都答对了7道题,由此可知,false题的正确答案依次是false false
题号选手
1
2
3
4
5
6
7
8
9
10
甲
false
false
false
false
false
false
false
false
false
false
乙
false
false
false
false
false
false
false
false
false
false
丙
false
false
false
false
false
false
false
false
false
false
A.false、false、false、false、false、false、false、false、false、false
B.false、false、false、false、false、false、false、false、false、false
C.false、false、false、false、false、false、false、false、false、false
D.false、false、false、false、false、false、false、false、false、false
二.多选题(共4小题)
9.下列有关回归分析的结论中,正确的有false false
A.运用最小二乘法求得的回归直线一定经过样本点的中心false,false
B.若相关系数false的绝对值越接近于1,则相关性越强
C.若相关指数false的值越接近于0,表示回归模型的拟合效果越好
D.在残差图中,残差点分布的带状区域的宽度越窄,说明模型拟合的精度越高
10.正方体false中,下列结论正确的是false false
A.直线false与直线false所成角为false
B.直线false与平面false所成角为false
C.二面角false的大小为false
D.平面false平面false
11.设直线false与圆false,则下列结论正确的为false false
A.false与false可能相离
B.false不可能将false的周长平分
C.当false时,false被false截得的弦长为false
D.false被false截得的最短弦长为4
12.已知false,false是正实数,且false,则下列说法中正确的有false false
A.false有最小值false
B.false有最小值4
C.false有最小值false
D.false有最小值7
三.填空题(共4小题)
13.已知false,false,若false是false的充分不必要条件,则实数false的取值范围是 .
14.写出一个以false为对称中心的偶函数 ,该函数的最小正周期是 .
15.已知向量false与false的夹角为false,且false,若false,其中false,则向量false在false上的投影的取值范围为 .
16.函数false的最大值为 ,记函数取到最大值时的false,则false .
四.解答题(共6小题)
17.已知数列false的前false项和为false,且false,false.数列false是公差大于0的等差数列,false,且false,false,false成等比数例.
(1)求数列false和false的通项公式;
(2)若false,求false.
18.已知false、false、false为false的三个内角,false、false、false是其三条边,false,false.
(1)若false,求false、false;
(2)若false,求false.
19.已知函数false,其中false.
(Ⅰ)若曲线false在false处的切线与直线false平行,求false的值;
(Ⅱ)若函数false在定义域内单调递减,求false的取值范围.
20.已知椭圆false的左,右焦点分别为false,false,且经过点false.
(1)求椭圆false的标准方程;
(2)若斜率为2的直线与椭圆false交于false,false两点,求false面积的最大值false为坐标原点).
21.如图,多面体false中,四边形false是菱形,false平面false,false,false,false,false.
(1)设点false为棱false的中点,求证:对任意的正数false,四边形false为平面四边形;
(2)当false时,求直线false与平面false所成角的正弦值.
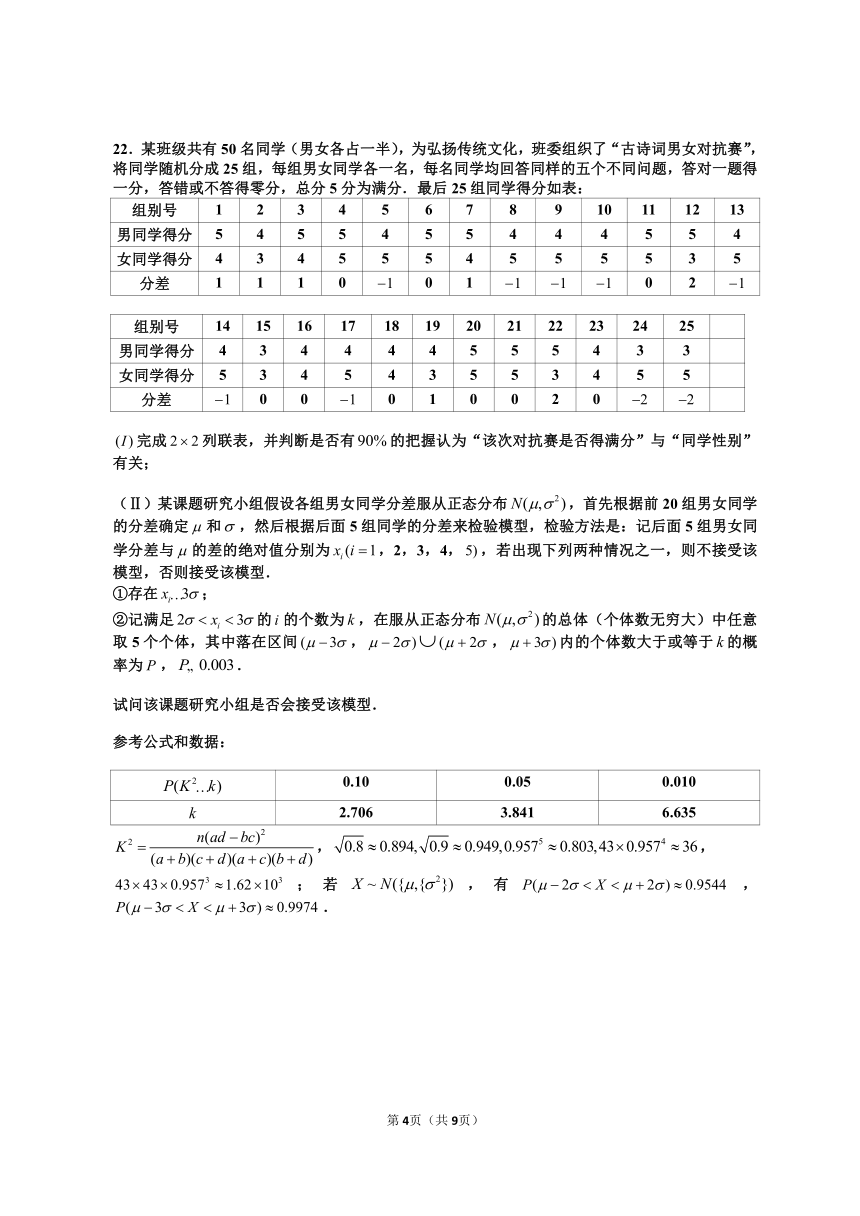
22.某班级共有50名同学(男女各占一半),为弘扬传统文化,班委组织了“古诗词男女对抗赛”,将同学随机分成25组,每组男女同学各一名,每名同学均回答同样的五个不同问题,答对一题得一分,答错或不答得零分,总分5分为满分.最后25组同学得分如表:
组别号
1
2
3
4
5
6
7
8
9
10
11
12
13
男同学得分
5
4
5
5
4
5
5
4
4
4
5
5
4
女同学得分
4
3
4
5
5
5
4
5
5
5
5
3
5
分差
1
1
1
0
false
0
1
false
false
false
0
2
false
组别号
14
15
16
17
18
19
20
21
22
23
24
25
男同学得分
4
3
4
4
4
4
5
5
5
4
3
3
女同学得分
5
3
4
5
4
3
5
5
3
4
5
5
分差
false
0
0
false
0
1
0
0
2
0
false
false
false完成false列联表,并判断是否有false的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
(Ⅱ)某课题研究小组假设各组男女同学分差服从正态分布false,首先根据前20组男女同学的分差确定false和false,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与false的差的绝对值分别为false,2,3,4,false,若出现下列两种情况之一,则不接受该模型,否则接受该模型.
①存在false;
②记满足false的false的个数为false,在服从正态分布false的总体(个体数无穷大)中任意取5个个体,其中落在区间false,false,false内的个体数大于或等于false的概率为false,false.
试问该课题研究小组是否会接受该模型.
参考公式和数据:
false
0.10
0.05
0.010
false
2.706
3.841
6.635
false,false,
false;若false,有false,false.
参考答案与试题解析
4705350135890一.选择题(共8小题)
1.【解答】解:根据条件,用false图表示false,false,false如下:由图看出,false.故选:false.
2.【解答】解:false复数false为虚部单位),false,
false,则当false时,false取最大值3.故选:false.
3.【解答】解:false双曲线false的虚轴长是实轴长的2倍,false其实轴长为4,可得false,
false.故选:false.
4.【解答】解:false,false,false,
false,falsefalse,false.故选:false.
5.【解答】解:false,false,
false,
false,false,false,
故选:false.
6.【解答】解:设等差数列false,false的通项公式分别为false,false,则false,令false,则falsefalse为等差数列,已知false,false,false,则false,false,false,false,false,可得数列false的公差为2,false,false.故选:false.
7.【解答】解:当false时,函数false的图象与二次函数false的图象有1个交点,由题意可得当false时,false与false有两个交点,由false,可得false,即false,设false,导数为false,当false时,false递减;当false时,false递增,可得false在false处取得极大值,且为最大值false,由false,解得false,故选:false.
8.【解答】解:甲与乙1,2,3,10题答案相同,false,false,false,false,
乙与丙2,4,5,7题答案相同,false,false,false,false,
甲与丙2,6,8,9题答案相同,false,false,false,false,
两两都有4题答案相同,6题不同,
因为都对7题,所有4题相同的都答对了,6题不同的各对了3道,
所有false题答案为:false,故选:false.
二.多选题(共4小题)
9.【解答】解:对于false,回归方程必定经过样本中心false,false,故选项false正确;
对于false,由相关系数的意义可知,相关系数false的绝对值越接近于1,则相关性越强,故选项false正确;
对于false,若相关指数false的值越接近于1,表示回归模型的拟合效果越好,故选项false错误;
对于false,在残差图中,残差点分布的带状区域的宽度越窄,说明模型拟合的精度越高,故选项false正确.故选:false.
4843145-7620010.【解答】解:对于false,连结false,false,因为false,故直线false与直线false所成角即为直线false与直线false所成角,因为false为正三角形,所以该角为false,故选项false正确;对于false,因为false平面false,所以直线false与平面false所成角为false,在false中,false,所以直线false与平面false所成角为false,故选项false错误;对于false,在正方体中可得,false,false,故二面角false的平面角为false,故选项false正确;对于false,设false,假设平面false平面false,又平面false平面false,false,故false平面false,因为false平面false,则false,而false与false不垂直,故假设不成立,故选项false错误.故选:false.
11.【解答】解:直线false恒过false,定点在圆的内部.圆的圆心false,半径为false,
所以直线不可能与圆相离,所以false不正确;直线可能经过圆的圆心,此时直线的倾斜角为false,所以直线不可能平方圆的周长,所以false正确;当false时,false化为false,圆心到直线的距离为:false,弦长为:false,所以false不正确;定点与圆心的距离为:1,最短弦长为:false,所以false正确.故选:false.
12.【解答】解:因为false,所以false,false,false当false时,等号成立,所以false正确;
因为false,所以false,false
false,当且仅当false时,等号成立,所以false错误;
false,当且仅当false时等号成立,所以false正确;
false,当且仅当false时等号成立,所以false错误;故选:false.
三.填空题(共4小题)
13.【解答】解:false,解得false,false,解得false,
false是false的充分不必要条件,falsefalse,解得false,则实数false的取值范围是false,false,故答案为:false,false.
14.【解答】解:选择一个具有对称性和周期性以及奇偶性的函数进行分析,故以false为对称中心的偶函数可以为false,该函数的最小正周期为false.故答案为:false;4.
52387505969015.【解答】解:如图所示,设false,false,false,false,false,false,又falsefalsefalsefalse,false在直线false上,当false与false同向时,即false与false重合时,false在false上的投影最大为false,作false,此时false在false上的投影为false,但取不到,falsefalse在false上的投影最小值大于false,falsefalse在false上的投影的范围为false,false.
16.【解答】解:false,令false,则false,则false,则函数的最大值为false,此时false,false,则false,则false,false,则false,故答案为:false,false.
四.解答题(共6小题)
17.【解答】解:(1)由false,可得false时,false,解得false;false时,false,化为false,则false;
false;
(2)false.
18.【解答】解:(1)因为false,可得false,又false,可得false,由于false,可得false.
(2)因为false,可得false,又false,可解得false,false,或false,false,因为false,可得false,false,若false,false,可得false,可得false,可得false为钝角,这与false为钝角矛盾,舍去,所以false,由正弦定理false,可得false.
19.【解答】解:(Ⅰ)数false的导数为false,由切线与直线false平行,可得false(1)false,即false,解得false;
(Ⅱ)函数false在定义域false内单调递减,可得false在false恒成立,
所以false,令false,false,由false,可得false,
所以当false时,false,false递减;当false时,false,false递增,可得false,故只需false,所以false的取值范围是false,false.
20.【解答】解:(1)由椭圆的定义,可知false.解得false.
又false.所以椭圆false的标准方程为false.
(2)设直线false的方程为false,联立椭圆方程,得false.△false,得false.设false,false,false,false,falsefalse,false
falsefalse,
点false到直线false的距离false
false,当false即false,false时取等;所以false面积的最大值为false.
4986655112395
21.【解答】(1)证明:设false在平面false内的射影为false,因为false,所以false,故点false在false的垂直平分线上,因为false是菱形,且false,故直线false与false的交点即为false的中点false,因为false平面false,false平面false,所以false,故false,false共面,所以false为平面四边形;
4947285329565(2)解:分别以false,false,false所在直线为false轴,false轴,false轴,建立空间直角坐标系如图所示,
则false,0,false,false,0,false,false,false,false,false,当false时,由false,又false为等腰三角形false的底边false的中点,故false,所以false,故false,又false,设false,false,false,则有false,解得false,设平面false的法向量为false,因为false,则有false,即false,令false,则false,故false,又false,所以false,故直线false与平面false所成角的正弦值为false.
22.【解答】解:false由表中数据,可得列联表;
男同学
女同学
总计
该次大赛得满分
10
14
24
该次大赛未得满分
15
11
26
总计
25
25
50
所以,计算false,所以没有false的把握说“该次大赛是否得满分”与“同学性别”有关;
(Ⅱ)由题意知,false,false;又false,false,false,false,false,而false,false,所以不存在false;又满足false的false的个数为3,即false;当false,false;设从服从正态分布false的总体(个体数无穷大)中任意取5个个体,其中值属于false,false,false的个体数为false,则false,所以,false;综上,第②种情况出现,所以该小组不会接受该模型.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/5/6
21:40:51;用户:497232607;邮箱:497232607@;学号:4383390
一.选择题(共8小题)
1.已知false,false是false的子集,且false,则false false
A.false
B.false
C.false
D.false
2.已知复数false为虚部单位),则false的最大值为false false
A.1
B.false
C.2
D.3
3.双曲线false的虚轴长是实轴长的2倍,则实数false的值是false false
A.16
B.false
C.false
D.false
4.设false,false,false,则false false
A.false
B.false
C.false
D.false
5.已知离散型随机变量false,false的分布列为
false
1
3
5
false
false
false
false
false
1
2
4
5
false
false
false
false
false
则下列说法一定正确的是false false
A.false
B.false
C.false
D.false
6.已知数列false,false均为等差数列,若false,false,false则false false
A.19
B.21
C.23
D.27
7.若指数函数false与函数false的图象恰有三个不同的交点,则实数false的取值范围是false false
A.false
B.false
C.false
D.false
8.甲、乙、丙三位同学参加学习脱贫干部黄文秀、戍边英雄陈红军、人民科学家南仁东、抗疫英雄张定宇等英雄的先进事迹知识竞赛.该竞赛共有十道判断题,三位同学的答题情况如下:考试成绩公布后,三个人都答对了7道题,由此可知,false题的正确答案依次是false false
题号选手
1
2
3
4
5
6
7
8
9
10
甲
false
false
false
false
false
false
false
false
false
false
乙
false
false
false
false
false
false
false
false
false
false
丙
false
false
false
false
false
false
false
false
false
false
A.false、false、false、false、false、false、false、false、false、false
B.false、false、false、false、false、false、false、false、false、false
C.false、false、false、false、false、false、false、false、false、false
D.false、false、false、false、false、false、false、false、false、false
二.多选题(共4小题)
9.下列有关回归分析的结论中,正确的有false false
A.运用最小二乘法求得的回归直线一定经过样本点的中心false,false
B.若相关系数false的绝对值越接近于1,则相关性越强
C.若相关指数false的值越接近于0,表示回归模型的拟合效果越好
D.在残差图中,残差点分布的带状区域的宽度越窄,说明模型拟合的精度越高
10.正方体false中,下列结论正确的是false false
A.直线false与直线false所成角为false
B.直线false与平面false所成角为false
C.二面角false的大小为false
D.平面false平面false
11.设直线false与圆false,则下列结论正确的为false false
A.false与false可能相离
B.false不可能将false的周长平分
C.当false时,false被false截得的弦长为false
D.false被false截得的最短弦长为4
12.已知false,false是正实数,且false,则下列说法中正确的有false false
A.false有最小值false
B.false有最小值4
C.false有最小值false
D.false有最小值7
三.填空题(共4小题)
13.已知false,false,若false是false的充分不必要条件,则实数false的取值范围是 .
14.写出一个以false为对称中心的偶函数 ,该函数的最小正周期是 .
15.已知向量false与false的夹角为false,且false,若false,其中false,则向量false在false上的投影的取值范围为 .
16.函数false的最大值为 ,记函数取到最大值时的false,则false .
四.解答题(共6小题)
17.已知数列false的前false项和为false,且false,false.数列false是公差大于0的等差数列,false,且false,false,false成等比数例.
(1)求数列false和false的通项公式;
(2)若false,求false.
18.已知false、false、false为false的三个内角,false、false、false是其三条边,false,false.
(1)若false,求false、false;
(2)若false,求false.
19.已知函数false,其中false.
(Ⅰ)若曲线false在false处的切线与直线false平行,求false的值;
(Ⅱ)若函数false在定义域内单调递减,求false的取值范围.
20.已知椭圆false的左,右焦点分别为false,false,且经过点false.
(1)求椭圆false的标准方程;
(2)若斜率为2的直线与椭圆false交于false,false两点,求false面积的最大值false为坐标原点).
21.如图,多面体false中,四边形false是菱形,false平面false,false,false,false,false.
(1)设点false为棱false的中点,求证:对任意的正数false,四边形false为平面四边形;
(2)当false时,求直线false与平面false所成角的正弦值.
22.某班级共有50名同学(男女各占一半),为弘扬传统文化,班委组织了“古诗词男女对抗赛”,将同学随机分成25组,每组男女同学各一名,每名同学均回答同样的五个不同问题,答对一题得一分,答错或不答得零分,总分5分为满分.最后25组同学得分如表:
组别号
1
2
3
4
5
6
7
8
9
10
11
12
13
男同学得分
5
4
5
5
4
5
5
4
4
4
5
5
4
女同学得分
4
3
4
5
5
5
4
5
5
5
5
3
5
分差
1
1
1
0
false
0
1
false
false
false
0
2
false
组别号
14
15
16
17
18
19
20
21
22
23
24
25
男同学得分
4
3
4
4
4
4
5
5
5
4
3
3
女同学得分
5
3
4
5
4
3
5
5
3
4
5
5
分差
false
0
0
false
0
1
0
0
2
0
false
false
false完成false列联表,并判断是否有false的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
(Ⅱ)某课题研究小组假设各组男女同学分差服从正态分布false,首先根据前20组男女同学的分差确定false和false,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与false的差的绝对值分别为false,2,3,4,false,若出现下列两种情况之一,则不接受该模型,否则接受该模型.
①存在false;
②记满足false的false的个数为false,在服从正态分布false的总体(个体数无穷大)中任意取5个个体,其中落在区间false,false,false内的个体数大于或等于false的概率为false,false.
试问该课题研究小组是否会接受该模型.
参考公式和数据:
false
0.10
0.05
0.010
false
2.706
3.841
6.635
false,false,
false;若false,有false,false.
参考答案与试题解析
4705350135890一.选择题(共8小题)
1.【解答】解:根据条件,用false图表示false,false,false如下:由图看出,false.故选:false.
2.【解答】解:false复数false为虚部单位),false,
false,则当false时,false取最大值3.故选:false.
3.【解答】解:false双曲线false的虚轴长是实轴长的2倍,false其实轴长为4,可得false,
false.故选:false.
4.【解答】解:false,false,false,
false,falsefalse,false.故选:false.
5.【解答】解:false,false,
false,
false,false,false,
故选:false.
6.【解答】解:设等差数列false,false的通项公式分别为false,false,则false,令false,则falsefalse为等差数列,已知false,false,false,则false,false,false,false,false,可得数列false的公差为2,false,false.故选:false.
7.【解答】解:当false时,函数false的图象与二次函数false的图象有1个交点,由题意可得当false时,false与false有两个交点,由false,可得false,即false,设false,导数为false,当false时,false递减;当false时,false递增,可得false在false处取得极大值,且为最大值false,由false,解得false,故选:false.
8.【解答】解:甲与乙1,2,3,10题答案相同,false,false,false,false,
乙与丙2,4,5,7题答案相同,false,false,false,false,
甲与丙2,6,8,9题答案相同,false,false,false,false,
两两都有4题答案相同,6题不同,
因为都对7题,所有4题相同的都答对了,6题不同的各对了3道,
所有false题答案为:false,故选:false.
二.多选题(共4小题)
9.【解答】解:对于false,回归方程必定经过样本中心false,false,故选项false正确;
对于false,由相关系数的意义可知,相关系数false的绝对值越接近于1,则相关性越强,故选项false正确;
对于false,若相关指数false的值越接近于1,表示回归模型的拟合效果越好,故选项false错误;
对于false,在残差图中,残差点分布的带状区域的宽度越窄,说明模型拟合的精度越高,故选项false正确.故选:false.
4843145-7620010.【解答】解:对于false,连结false,false,因为false,故直线false与直线false所成角即为直线false与直线false所成角,因为false为正三角形,所以该角为false,故选项false正确;对于false,因为false平面false,所以直线false与平面false所成角为false,在false中,false,所以直线false与平面false所成角为false,故选项false错误;对于false,在正方体中可得,false,false,故二面角false的平面角为false,故选项false正确;对于false,设false,假设平面false平面false,又平面false平面false,false,故false平面false,因为false平面false,则false,而false与false不垂直,故假设不成立,故选项false错误.故选:false.
11.【解答】解:直线false恒过false,定点在圆的内部.圆的圆心false,半径为false,
所以直线不可能与圆相离,所以false不正确;直线可能经过圆的圆心,此时直线的倾斜角为false,所以直线不可能平方圆的周长,所以false正确;当false时,false化为false,圆心到直线的距离为:false,弦长为:false,所以false不正确;定点与圆心的距离为:1,最短弦长为:false,所以false正确.故选:false.
12.【解答】解:因为false,所以false,false,false当false时,等号成立,所以false正确;
因为false,所以false,false
false,当且仅当false时,等号成立,所以false错误;
false,当且仅当false时等号成立,所以false正确;
false,当且仅当false时等号成立,所以false错误;故选:false.
三.填空题(共4小题)
13.【解答】解:false,解得false,false,解得false,
false是false的充分不必要条件,falsefalse,解得false,则实数false的取值范围是false,false,故答案为:false,false.
14.【解答】解:选择一个具有对称性和周期性以及奇偶性的函数进行分析,故以false为对称中心的偶函数可以为false,该函数的最小正周期为false.故答案为:false;4.
52387505969015.【解答】解:如图所示,设false,false,false,false,false,false,又falsefalsefalsefalse,false在直线false上,当false与false同向时,即false与false重合时,false在false上的投影最大为false,作false,此时false在false上的投影为false,但取不到,falsefalse在false上的投影最小值大于false,falsefalse在false上的投影的范围为false,false.
16.【解答】解:false,令false,则false,则false,则函数的最大值为false,此时false,false,则false,则false,false,则false,故答案为:false,false.
四.解答题(共6小题)
17.【解答】解:(1)由false,可得false时,false,解得false;false时,false,化为false,则false;
false;
(2)false.
18.【解答】解:(1)因为false,可得false,又false,可得false,由于false,可得false.
(2)因为false,可得false,又false,可解得false,false,或false,false,因为false,可得false,false,若false,false,可得false,可得false,可得false为钝角,这与false为钝角矛盾,舍去,所以false,由正弦定理false,可得false.
19.【解答】解:(Ⅰ)数false的导数为false,由切线与直线false平行,可得false(1)false,即false,解得false;
(Ⅱ)函数false在定义域false内单调递减,可得false在false恒成立,
所以false,令false,false,由false,可得false,
所以当false时,false,false递减;当false时,false,false递增,可得false,故只需false,所以false的取值范围是false,false.
20.【解答】解:(1)由椭圆的定义,可知false.解得false.
又false.所以椭圆false的标准方程为false.
(2)设直线false的方程为false,联立椭圆方程,得false.△false,得false.设false,false,false,false,falsefalse,false
falsefalse,
点false到直线false的距离false
false,当false即false,false时取等;所以false面积的最大值为false.
4986655112395
21.【解答】(1)证明:设false在平面false内的射影为false,因为false,所以false,故点false在false的垂直平分线上,因为false是菱形,且false,故直线false与false的交点即为false的中点false,因为false平面false,false平面false,所以false,故false,false共面,所以false为平面四边形;
4947285329565(2)解:分别以false,false,false所在直线为false轴,false轴,false轴,建立空间直角坐标系如图所示,
则false,0,false,false,0,false,false,false,false,false,当false时,由false,又false为等腰三角形false的底边false的中点,故false,所以false,故false,又false,设false,false,false,则有false,解得false,设平面false的法向量为false,因为false,则有false,即false,令false,则false,故false,又false,所以false,故直线false与平面false所成角的正弦值为false.
22.【解答】解:false由表中数据,可得列联表;
男同学
女同学
总计
该次大赛得满分
10
14
24
该次大赛未得满分
15
11
26
总计
25
25
50
所以,计算false,所以没有false的把握说“该次大赛是否得满分”与“同学性别”有关;
(Ⅱ)由题意知,false,false;又false,false,false,false,false,而false,false,所以不存在false;又满足false的false的个数为3,即false;当false,false;设从服从正态分布false的总体(个体数无穷大)中任意取5个个体,其中值属于false,false,false的个体数为false,则false,所以,false;综上,第②种情况出现,所以该小组不会接受该模型.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2021/5/6
21:40:51;用户:497232607;邮箱:497232607@;学号:4383390
同课章节目录
