2021年 华师大版 七年级数学下册 9.1 三角形 同步练习题(Word版 含解析)
文档属性
| 名称 | 2021年 华师大版 七年级数学下册 9.1 三角形 同步练习题(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 06:32:51 | ||
图片预览



文档简介
2021年华师大版七年级下册9.1《三角形》同步练习题
一.选择题
1.已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
A.40° B.60° C.80° D.90°
2.下列长度的三条线段,不能组成三角形的是( )
A.a+1,a+2,a+3(a>0) B.3a,5a,2a+1(a>0)
C.三条线段之比为1:2:3 D.5cm,6cm,10cm
3.下列说法中错误的是( )
A.一个三角形中至少有一个角不少于60°
B.三角形的中线不可能在三角形的外部
C.周长相等的两个三角形全等
D.三角形的中线把三角形的面积平均分成相等的两部分
4.下图能说明∠1>∠2一定成立的是( )
A. B.
C. D.
5.如图,点P在△ABC内,则下列叙述正确的是( )
A.x°=y° B.x°>y° C.x°<y° D.不能确定
6.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.11 D.16
7.下列图形中具有稳定性有( )
A.2个 B.3个 C.4个 D.5个
8.一个多边形的内角和是900°,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
9.如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
A.120° B.180° C.240° D.300°
10.已知a,b,c是三角形的三边长,化简:|a﹣b+c|﹣|a﹣b﹣c|的值为( )
A.2a B.2b C.2a﹣2b D.2a+2b
11.等腰三角形的两边长分别为2cm和7cm,则其周长为( )
A.11cm B.13cm C.16cm D.11cm或16cm
12.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C,⑤∠A=2∠B=3∠C中,能确定△ABC是直角三角形的条件有( )
A.2个 B.3个 C.4个 D.5个
二.填空题
13.在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于点P,若∠A=50°,则∠BPC的度数是 度.
14.用正方形和正方形组合能够铺满地面,每个顶点周围有m个正三角形和n个正方形,则m+n= .
15.十边形的外角和是 度;如果十边形的各个内角都相等,那么它的一个内角是 度.
三.解答题
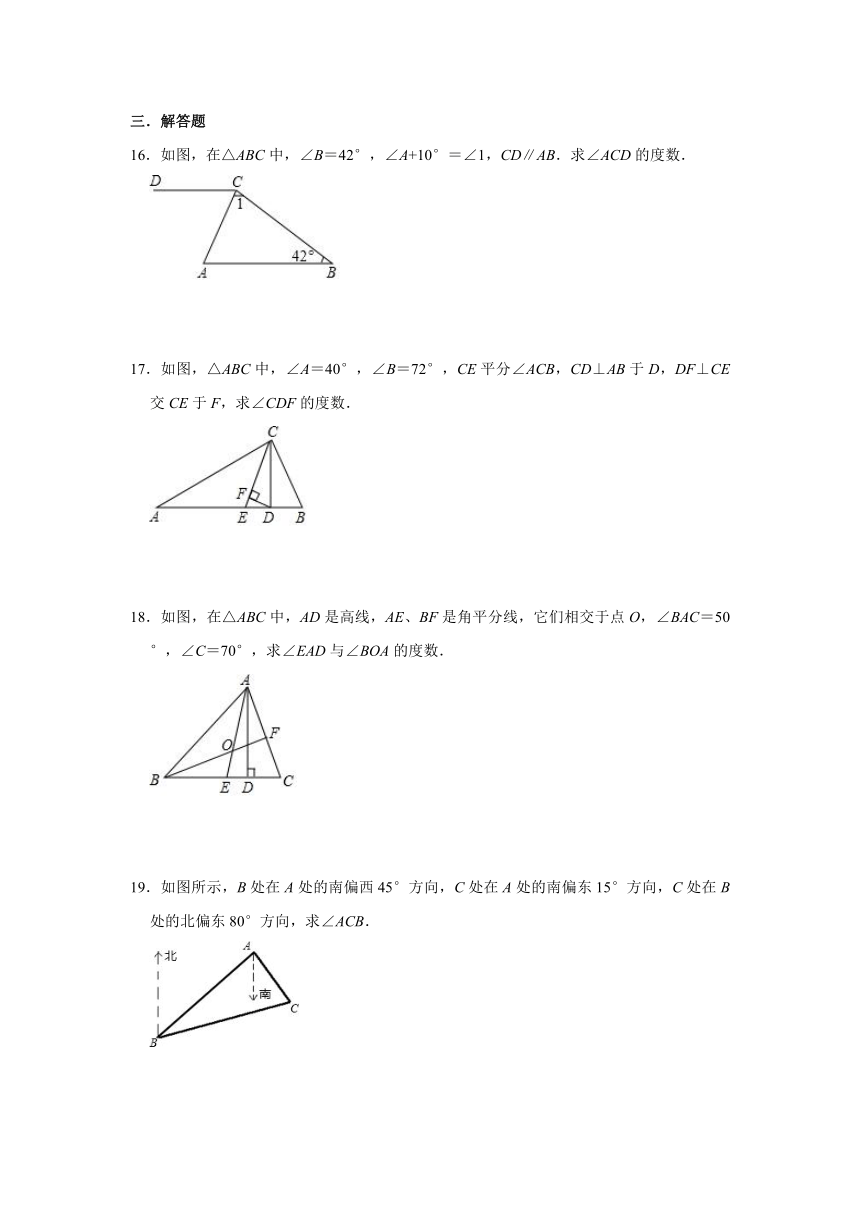
16.如图,在△ABC中,∠B=42°,∠A+10°=∠1,CD∥AB.求∠ACD的度数.
17.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE交CE于F,求∠CDF的度数.
18.如图,在△ABC中,AD是高线,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠EAD与∠BOA的度数.
19.如图所示,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB.
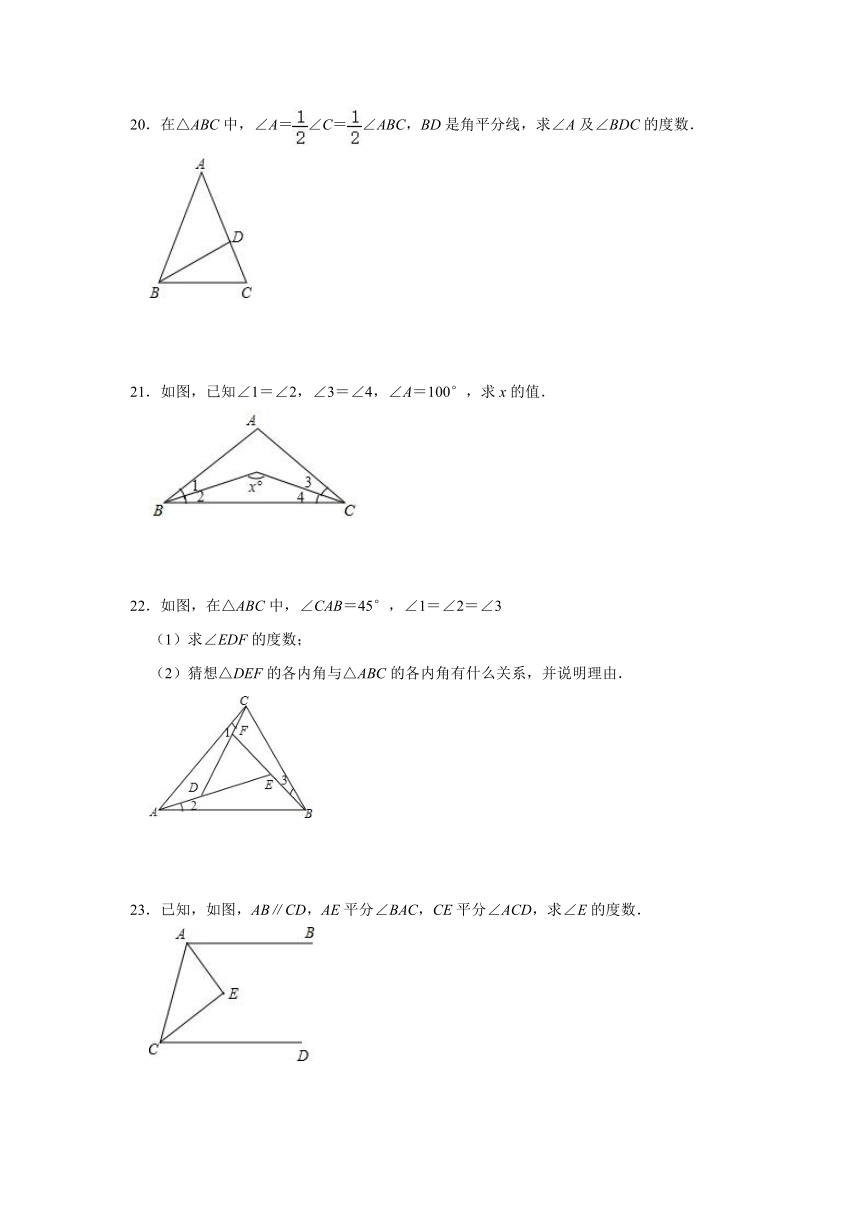
20.在△ABC中,∠A=∠C=∠ABC,BD是角平分线,求∠A及∠BDC的度数.
21.如图,已知∠1=∠2,∠3=∠4,∠A=100°,求x的值.
22.如图,在△ABC中,∠CAB=45°,∠1=∠2=∠3
(1)求∠EDF的度数;
(2)猜想△DEF的各内角与△ABC的各内角有什么关系,并说明理由.
23.已知,如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E的度数.
24.(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:
∠1+∠2 ∠B+∠C(填“>”“<”“=”),当∠A=60°时,∠B+∠C+∠1+∠2=
(3)如图③,是由图①的△ABC沿DE折叠得到的,猜想∠BDA+∠CEA与∠A的关系,并证明你的猜想.
参考答案
一.选择题
1.解:设∠A=x,则∠B=2x,∠C=x+20°,则x+2x+x+20°=180°,解得x=40°,即∠A=40°.
故选:A.
2.解:A、a+1+(a+2)=2a+3>a+3,故可以构成三角形;
B、3a+(2a+1)=5a+1>5a,故可以构成三角形;
C、1+2=3,不满足三边关系定理,因而不能构成三角形;
D、5cm+6cm>10cm,故可以构成三角形.
故选:C.
3.解:A、∵三角形的内角和等于180°,
∴一个三角形中至少有一个角不少于60°,故本选项正确;
B、三角形的中线一定在三角形的内部,故本选项正确;
C、周长相等的三角形不一定全等,故本选项错误;
D、三角形的中线把三角形的面积平均分成相等的两部分,故本选项正确;
故选:C.
4.解:A、D选项∠1=∠2,
B选项不能说明∠1>∠2,
C选项∠1>∠2.
故选:C.
5.解:延长BP与AC相交于点D,则∠BPC>∠BDC>∠A,
∴x°<y°.
故选:C.
6.解:设此三角形第三边的长为x,则10﹣4<x<10+4,即6<x<14,四个选项中只有11符合条件.
故选:C.
7.解:根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性.显然(2)、(4)、(5)三个.故选B.
8.解:设这个多边形的边数为n,
则有(n﹣2)180°=900°,
解得:n=7,
∴这个多边形的边数为7.
故选:B.
9.解:根据三角形的内角和定理得:
四边形除去∠1,∠2后的两角的度数为180°﹣60°=120°,
则根据四边形的内角和定理得:
∠1+∠2=360°﹣120°=240°.
故选:C.
10.解:根据三角形的三边关系,得
a﹣b+c>0,a﹣b﹣c<0.
|a﹣b+c|﹣|a﹣b﹣c|=a﹣b+c+(a﹣b﹣c)=2a﹣2b.
故选:C.
11.解:当腰长是2cm时,因为2+2<7,不符合三角形的三边关系,应排除;
当腰长是7cm时,7,7,2符合三角形三边关系,此时周长是16cm.
故选:C.
12.解:①因为∠A+∠B=∠C,则2∠C=180°,∠C=90°,所以△ABC是直角三角形;
②因为∠A:∠B:∠C=1:2:3,设∠A=x,则x+2x+3x=180,x=30°,∠C=30°×3=90°,所以△ABC是直角三角形;
③因为∠A=90°﹣∠B,所以∠A+∠B=90°,则∠C=180°﹣90°=90°,所以△ABC是直角三角形;
④因为∠A=∠B=∠C,所以∠A+∠B+∠C=∠C+∠C+∠C=180°,则∠C=90°,所以△ABC是直角三角形;
⑤因为3∠C=2∠B=∠A,∠A+∠B+∠C=∠A+∠A+∠A=180°,∠A=,所以△ABC为钝角三角形.
所以能确定△ABC是直角三角形的有①②③④共4个,
故选:C.
二.填空题
13.解:∵CD,BE分别是AB,AC边上的高,
∴∠BDC=∠AEB=90°
∴∠ABE=90°﹣50°=40°
∴∠BPC=∠ABE+∠BDP=40+90=130°.
故答案为:130°.
14.解:∵正三角形和正方形的一个内角分别是60°,90°,
而3×60°+2×90°=360°,
∴m=3,n=2,
∴m+n=5.
故答案为:5.
15.解:∵任何多边形的外角和都等于360度,
∴十边形的外角和是360度;
∵每个外角的度数是360°÷10=36°,
∴它的一个内角是180°﹣36°=144度.
三.解答题
16.解:∵∠A+∠B+∠1=180°,
而∠B=42°,∠A+10°=∠1,
∴∠A+42°+∠A+10°=180°,
∵AB∥CD.
∴∠ACD=∠A=64°.
17.解:∵∠A=40°,∠B=72°,
∴∠ACB=180°﹣40°﹣72°=68°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=34°,
∴∠CED=∠A+∠ACE=74°,
∵∠CDE=90°,DF⊥CE,
∴∠CDF+∠ECD=∠ECD+∠CED=90°,
∴∠CDF=74°.
18.解:∵AD⊥BC
∴∠ADC=90°
∵∠C=70°
∴∠DAC=180°﹣90°﹣70°=20°,
∵AE平分∠BAC,
∴∠CAE=×50°=25°
∴∠EAD=∠EAC﹣∠DAC=25°﹣20°=5°;
∵∠BAC=50°,∠C=70°
∴∠BAO=25°,∠ABC=60°
∵BF是∠ABC的角平分线
∴∠ABO=30°
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°.
19.解:∵AE,DB是正南正北方向,
∴BD∥AE,
∵∠DBA=45°,
∴∠BAE=∠DBA=45°,
∵∠EAC=15°,
∴∠BAC=∠BAE+∠EAC=45°+15°=60°,
又∵∠DBC=80°,
∴∠ABC=80°﹣45°=35°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣60°﹣35°=85°.
20.解:∵∠A=∠C=∠ABC,∠A+∠B+∠C=180°,
∴∠A=36°,∠ABC=∠C=72°,
∵BD是角平分线,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠BDC=72°.
答:∠A的度数是36°,∠BDC的度数是72°.
21.解:∵∠A=100°,
∴∠ABC+∠ACB=180°﹣∠A=80°,
即∠1+∠2+∠3+∠4=80°,
∵∠1=∠2,∠3=∠4,
∴2∠2+2∠4=80°,
∴∠2+∠4=40°,
∴x=180°﹣(∠2+∠4)
=180°﹣40°
=140°.
22.解:(1)在△ACD中,∠EDF=∠1+∠CAE,
∵∠1=∠2,
∴∠EDF=∠2+∠CAE=∠BAC=45°.
(2)△DEF的各内角与△ABC的各内角相等.
理由如下:
∵∠EDF=∠1+∠CAE,∠FED=∠2+∠ABF,∠EFD=∠3+∠BCD,∠1=∠2=∠3,
∴∠EDF=∠2+∠CAE=∠BAC,∠FED=∠3+∠ABF=∠ABC,∠EFD=∠1+∠BCD=∠BCA.
23.解:∵AB∥CD,AE平分∠BAC,CE平分∠ACD,
又∠BAC+∠DCA=180°?∠CAE+∠ACE=(∠BAC+∠DCA)=90°,
∠E=180°﹣(∠CAE+∠ACE)=90°,
∴∠E=90°.
24.解:(1)根据三角形内角是180°,
可知:∠1+∠2=180°﹣∠A,∠B+∠C=180°﹣∠A,
∴∠1+∠2=∠B+∠C;
(2)∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°,
∴∠1+∠2=∠B+∠C;
当∠A=60°时,∠B+∠C+∠1+∠2=120×2=240°;
故答案为:=;240°
(3)如图③,延长BD交CE的延长线于A′.
∵∠BDA=∠DA′A+∠DAA′,∠AEC=∠EA′A+∠EAA′,∠DA′E=∠DAE,
∴∠BDA+∠AEC=2∠DAE,
∴∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
一.选择题
1.已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
A.40° B.60° C.80° D.90°
2.下列长度的三条线段,不能组成三角形的是( )
A.a+1,a+2,a+3(a>0) B.3a,5a,2a+1(a>0)
C.三条线段之比为1:2:3 D.5cm,6cm,10cm
3.下列说法中错误的是( )
A.一个三角形中至少有一个角不少于60°
B.三角形的中线不可能在三角形的外部
C.周长相等的两个三角形全等
D.三角形的中线把三角形的面积平均分成相等的两部分
4.下图能说明∠1>∠2一定成立的是( )
A. B.
C. D.
5.如图,点P在△ABC内,则下列叙述正确的是( )
A.x°=y° B.x°>y° C.x°<y° D.不能确定
6.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.11 D.16
7.下列图形中具有稳定性有( )
A.2个 B.3个 C.4个 D.5个
8.一个多边形的内角和是900°,则这个多边形的边数是( )
A.6 B.7 C.8 D.9
9.如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
A.120° B.180° C.240° D.300°
10.已知a,b,c是三角形的三边长,化简:|a﹣b+c|﹣|a﹣b﹣c|的值为( )
A.2a B.2b C.2a﹣2b D.2a+2b
11.等腰三角形的两边长分别为2cm和7cm,则其周长为( )
A.11cm B.13cm C.16cm D.11cm或16cm
12.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C,⑤∠A=2∠B=3∠C中,能确定△ABC是直角三角形的条件有( )
A.2个 B.3个 C.4个 D.5个
二.填空题
13.在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于点P,若∠A=50°,则∠BPC的度数是 度.
14.用正方形和正方形组合能够铺满地面,每个顶点周围有m个正三角形和n个正方形,则m+n= .
15.十边形的外角和是 度;如果十边形的各个内角都相等,那么它的一个内角是 度.
三.解答题
16.如图,在△ABC中,∠B=42°,∠A+10°=∠1,CD∥AB.求∠ACD的度数.
17.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE交CE于F,求∠CDF的度数.
18.如图,在△ABC中,AD是高线,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠EAD与∠BOA的度数.
19.如图所示,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB.
20.在△ABC中,∠A=∠C=∠ABC,BD是角平分线,求∠A及∠BDC的度数.
21.如图,已知∠1=∠2,∠3=∠4,∠A=100°,求x的值.
22.如图,在△ABC中,∠CAB=45°,∠1=∠2=∠3
(1)求∠EDF的度数;
(2)猜想△DEF的各内角与△ABC的各内角有什么关系,并说明理由.
23.已知,如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E的度数.
24.(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:
∠1+∠2 ∠B+∠C(填“>”“<”“=”),当∠A=60°时,∠B+∠C+∠1+∠2=
(3)如图③,是由图①的△ABC沿DE折叠得到的,猜想∠BDA+∠CEA与∠A的关系,并证明你的猜想.
参考答案
一.选择题
1.解:设∠A=x,则∠B=2x,∠C=x+20°,则x+2x+x+20°=180°,解得x=40°,即∠A=40°.
故选:A.
2.解:A、a+1+(a+2)=2a+3>a+3,故可以构成三角形;
B、3a+(2a+1)=5a+1>5a,故可以构成三角形;
C、1+2=3,不满足三边关系定理,因而不能构成三角形;
D、5cm+6cm>10cm,故可以构成三角形.
故选:C.
3.解:A、∵三角形的内角和等于180°,
∴一个三角形中至少有一个角不少于60°,故本选项正确;
B、三角形的中线一定在三角形的内部,故本选项正确;
C、周长相等的三角形不一定全等,故本选项错误;
D、三角形的中线把三角形的面积平均分成相等的两部分,故本选项正确;
故选:C.
4.解:A、D选项∠1=∠2,
B选项不能说明∠1>∠2,
C选项∠1>∠2.
故选:C.
5.解:延长BP与AC相交于点D,则∠BPC>∠BDC>∠A,
∴x°<y°.
故选:C.
6.解:设此三角形第三边的长为x,则10﹣4<x<10+4,即6<x<14,四个选项中只有11符合条件.
故选:C.
7.解:根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性.显然(2)、(4)、(5)三个.故选B.
8.解:设这个多边形的边数为n,
则有(n﹣2)180°=900°,
解得:n=7,
∴这个多边形的边数为7.
故选:B.
9.解:根据三角形的内角和定理得:
四边形除去∠1,∠2后的两角的度数为180°﹣60°=120°,
则根据四边形的内角和定理得:
∠1+∠2=360°﹣120°=240°.
故选:C.
10.解:根据三角形的三边关系,得
a﹣b+c>0,a﹣b﹣c<0.
|a﹣b+c|﹣|a﹣b﹣c|=a﹣b+c+(a﹣b﹣c)=2a﹣2b.
故选:C.
11.解:当腰长是2cm时,因为2+2<7,不符合三角形的三边关系,应排除;
当腰长是7cm时,7,7,2符合三角形三边关系,此时周长是16cm.
故选:C.
12.解:①因为∠A+∠B=∠C,则2∠C=180°,∠C=90°,所以△ABC是直角三角形;
②因为∠A:∠B:∠C=1:2:3,设∠A=x,则x+2x+3x=180,x=30°,∠C=30°×3=90°,所以△ABC是直角三角形;
③因为∠A=90°﹣∠B,所以∠A+∠B=90°,则∠C=180°﹣90°=90°,所以△ABC是直角三角形;
④因为∠A=∠B=∠C,所以∠A+∠B+∠C=∠C+∠C+∠C=180°,则∠C=90°,所以△ABC是直角三角形;
⑤因为3∠C=2∠B=∠A,∠A+∠B+∠C=∠A+∠A+∠A=180°,∠A=,所以△ABC为钝角三角形.
所以能确定△ABC是直角三角形的有①②③④共4个,
故选:C.
二.填空题
13.解:∵CD,BE分别是AB,AC边上的高,
∴∠BDC=∠AEB=90°
∴∠ABE=90°﹣50°=40°
∴∠BPC=∠ABE+∠BDP=40+90=130°.
故答案为:130°.
14.解:∵正三角形和正方形的一个内角分别是60°,90°,
而3×60°+2×90°=360°,
∴m=3,n=2,
∴m+n=5.
故答案为:5.
15.解:∵任何多边形的外角和都等于360度,
∴十边形的外角和是360度;
∵每个外角的度数是360°÷10=36°,
∴它的一个内角是180°﹣36°=144度.
三.解答题
16.解:∵∠A+∠B+∠1=180°,
而∠B=42°,∠A+10°=∠1,
∴∠A+42°+∠A+10°=180°,
∵AB∥CD.
∴∠ACD=∠A=64°.
17.解:∵∠A=40°,∠B=72°,
∴∠ACB=180°﹣40°﹣72°=68°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=34°,
∴∠CED=∠A+∠ACE=74°,
∵∠CDE=90°,DF⊥CE,
∴∠CDF+∠ECD=∠ECD+∠CED=90°,
∴∠CDF=74°.
18.解:∵AD⊥BC
∴∠ADC=90°
∵∠C=70°
∴∠DAC=180°﹣90°﹣70°=20°,
∵AE平分∠BAC,
∴∠CAE=×50°=25°
∴∠EAD=∠EAC﹣∠DAC=25°﹣20°=5°;
∵∠BAC=50°,∠C=70°
∴∠BAO=25°,∠ABC=60°
∵BF是∠ABC的角平分线
∴∠ABO=30°
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°.
19.解:∵AE,DB是正南正北方向,
∴BD∥AE,
∵∠DBA=45°,
∴∠BAE=∠DBA=45°,
∵∠EAC=15°,
∴∠BAC=∠BAE+∠EAC=45°+15°=60°,
又∵∠DBC=80°,
∴∠ABC=80°﹣45°=35°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=180°﹣60°﹣35°=85°.
20.解:∵∠A=∠C=∠ABC,∠A+∠B+∠C=180°,
∴∠A=36°,∠ABC=∠C=72°,
∵BD是角平分线,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠BDC=72°.
答:∠A的度数是36°,∠BDC的度数是72°.
21.解:∵∠A=100°,
∴∠ABC+∠ACB=180°﹣∠A=80°,
即∠1+∠2+∠3+∠4=80°,
∵∠1=∠2,∠3=∠4,
∴2∠2+2∠4=80°,
∴∠2+∠4=40°,
∴x=180°﹣(∠2+∠4)
=180°﹣40°
=140°.
22.解:(1)在△ACD中,∠EDF=∠1+∠CAE,
∵∠1=∠2,
∴∠EDF=∠2+∠CAE=∠BAC=45°.
(2)△DEF的各内角与△ABC的各内角相等.
理由如下:
∵∠EDF=∠1+∠CAE,∠FED=∠2+∠ABF,∠EFD=∠3+∠BCD,∠1=∠2=∠3,
∴∠EDF=∠2+∠CAE=∠BAC,∠FED=∠3+∠ABF=∠ABC,∠EFD=∠1+∠BCD=∠BCA.
23.解:∵AB∥CD,AE平分∠BAC,CE平分∠ACD,
又∠BAC+∠DCA=180°?∠CAE+∠ACE=(∠BAC+∠DCA)=90°,
∠E=180°﹣(∠CAE+∠ACE)=90°,
∴∠E=90°.
24.解:(1)根据三角形内角是180°,
可知:∠1+∠2=180°﹣∠A,∠B+∠C=180°﹣∠A,
∴∠1+∠2=∠B+∠C;
(2)∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°,
∴∠1+∠2=∠B+∠C;
当∠A=60°时,∠B+∠C+∠1+∠2=120×2=240°;
故答案为:=;240°
(3)如图③,延长BD交CE的延长线于A′.
∵∠BDA=∠DA′A+∠DAA′,∠AEC=∠EA′A+∠EAA′,∠DA′E=∠DAE,
∴∠BDA+∠AEC=2∠DAE,
∴∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
