鲁教版(五四制)七年级下册数学 第八章 平行线的有关证明(复习) 教案
文档属性
| 名称 | 鲁教版(五四制)七年级下册数学 第八章 平行线的有关证明(复习) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 69.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 00:00:00 | ||
图片预览

文档简介
《平行线的有关证明》复习课
---------教学设计
教学目标:
知识目标:1.了解定义、命题
2.掌握并运用平行线的判定定理、性质定理
3.掌握并运用三角形的内角和定理、外角、外角定理
能力目标:发展学生的推理能力
教学重点:平行线的判定定理、性质定理
三角形的内角和定理、外角、外角定理
教学难点:知识的融会贯通
教学过程:(一)三角形
我们先来看一个最熟悉的几何图形——三角形,在本章中我们学习了三角形的角的哪些知识?(学生口答)
课堂练习(一)
1.△ABC中,∠A+∠B=120°,∠C=2∠A,则∠A=___,∠B=_____.
2、已知:如图,△ABC中,∠B=50°,AE是∠BAC的平分线,∠ACD=120°,则∠BAC=________,∠AEC=____________.
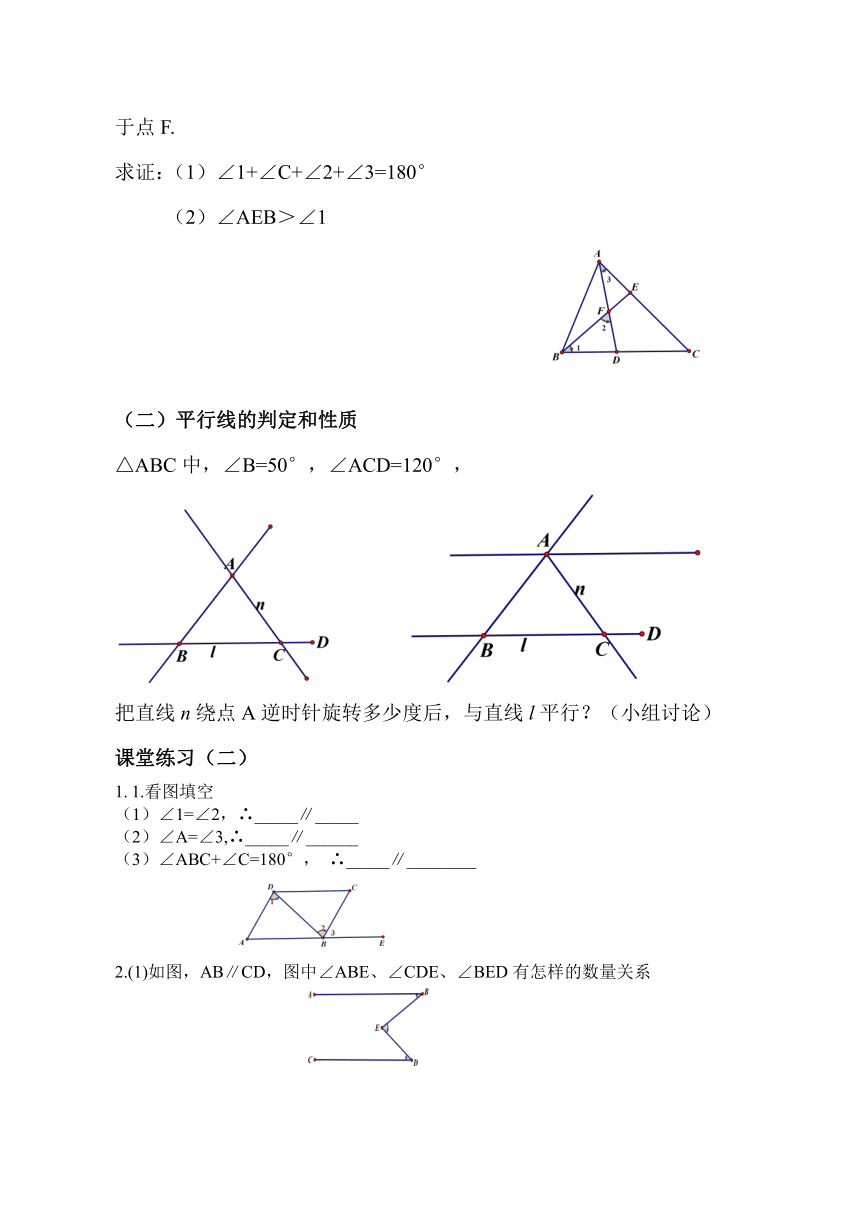
3、如图,△ABC中,点D,E分别是BC,AC上的点,AD,BE相交于点F.
求证:(1)∠1+∠C+∠2+∠3=180°
(2)∠AEB>∠1
(二)平行线的判定和性质
△ABC中,∠B=50°,∠ACD=120°,
把直线n绕点A逆时针旋转多少度后,与直线l平行?(小组讨论)
课堂练习(二)
1. 1.看图填空
(1)∠1=∠2,∴_____∥_____
(2)∠A=∠3,∴_____∥______
(3)∠ABC+∠C=180°, ∴_____∥________
2.(1)如图,AB∥CD,图中∠ABE、∠CDE、∠BED有怎样的数量关系
(2) AB∥CD,下面的两个图形中∠ABE、∠CDE、∠BED分别有怎样的数量关系
课堂检测
1.下列语句不是命题的是( )
A.同角的余角相等
B.作直线AB的垂线
C.若a - c=b - c,则a = b
D.两直线相交,只有一个交点
2.下列命题中,是真命题的是( )
A.在同一平面内,垂直于同一直线的两条直线平行
B.相等的角是对顶角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
3.如图,直线a∥b,直角三角形如图放置,∠DCB=90°,
若∠1+∠B=70°,则∠2的度数为________
4.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB
(2)求∠DFC的度数
拓展提高
在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高.
求证:∠A=2∠DBC
.
课堂小结:说一说自己在本节课的收获(知识和方法)
---------教学设计
教学目标:
知识目标:1.了解定义、命题
2.掌握并运用平行线的判定定理、性质定理
3.掌握并运用三角形的内角和定理、外角、外角定理
能力目标:发展学生的推理能力
教学重点:平行线的判定定理、性质定理
三角形的内角和定理、外角、外角定理
教学难点:知识的融会贯通
教学过程:(一)三角形
我们先来看一个最熟悉的几何图形——三角形,在本章中我们学习了三角形的角的哪些知识?(学生口答)
课堂练习(一)
1.△ABC中,∠A+∠B=120°,∠C=2∠A,则∠A=___,∠B=_____.
2、已知:如图,△ABC中,∠B=50°,AE是∠BAC的平分线,∠ACD=120°,则∠BAC=________,∠AEC=____________.
3、如图,△ABC中,点D,E分别是BC,AC上的点,AD,BE相交于点F.
求证:(1)∠1+∠C+∠2+∠3=180°
(2)∠AEB>∠1
(二)平行线的判定和性质
△ABC中,∠B=50°,∠ACD=120°,
把直线n绕点A逆时针旋转多少度后,与直线l平行?(小组讨论)
课堂练习(二)
1. 1.看图填空
(1)∠1=∠2,∴_____∥_____
(2)∠A=∠3,∴_____∥______
(3)∠ABC+∠C=180°, ∴_____∥________
2.(1)如图,AB∥CD,图中∠ABE、∠CDE、∠BED有怎样的数量关系
(2) AB∥CD,下面的两个图形中∠ABE、∠CDE、∠BED分别有怎样的数量关系
课堂检测
1.下列语句不是命题的是( )
A.同角的余角相等
B.作直线AB的垂线
C.若a - c=b - c,则a = b
D.两直线相交,只有一个交点
2.下列命题中,是真命题的是( )
A.在同一平面内,垂直于同一直线的两条直线平行
B.相等的角是对顶角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
3.如图,直线a∥b,直角三角形如图放置,∠DCB=90°,
若∠1+∠B=70°,则∠2的度数为________
4.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB
(2)求∠DFC的度数
拓展提高
在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高.
求证:∠A=2∠DBC
.
课堂小结:说一说自己在本节课的收获(知识和方法)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
