苏科版七年级下册数学课件:第11章 一元一次不等式小结与思考(17张)
文档属性
| 名称 | 苏科版七年级下册数学课件:第11章 一元一次不等式小结与思考(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 10:15:01 | ||
图片预览




文档简介
《一元一次不等式(组)》复习
初中数学七年级下册
(苏科版)
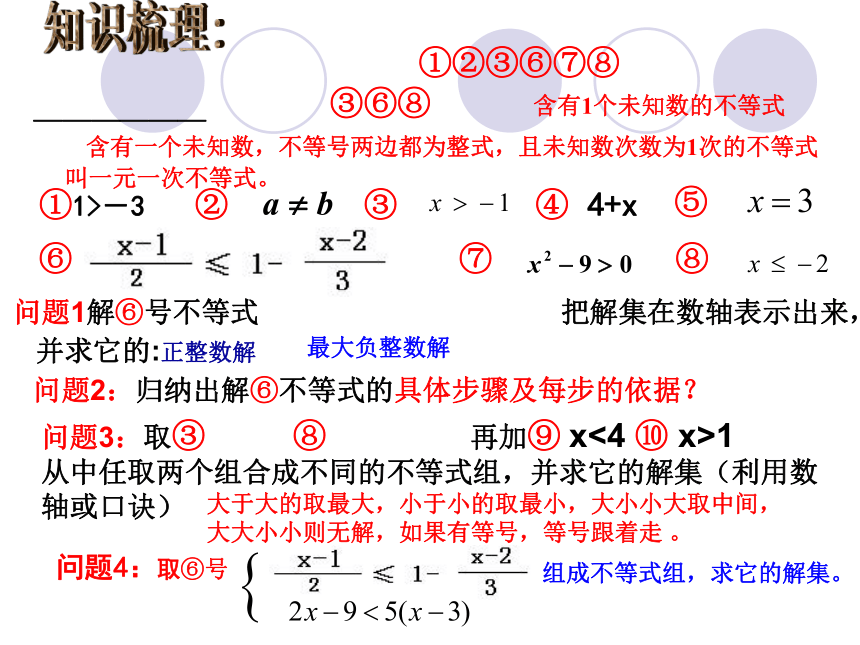
③
______
⑥
⑧
①1>-3
②
④ 4+x
⑦
⑤
问题1解⑥号不等式 把解集在数轴表示出来,
问题2:归纳出解⑥不等式的具体步骤及每步的依据?
并求它的:正整数解
最大负整数解
①②③⑥⑦⑧
③⑥⑧
问题3:取③ ⑧ 再加⑨ x<4 ⑩ x>1
从中任取两个组合成不同的不等式组,并求它的解集(利用数轴或口诀)
含有1个未知数的不等式
含有一个未知数,不等号两边都为整式,且未知数次数为1次的不等式
叫一元一次不等式。
大于大的取最大,小于小的取最小,大小小大取中间,
大大小小则无解,如果有等号,等号跟着走 。
问题4:取⑥号
组成不等式组,求它的解集。
2、根据实际问题列出不等量关系
P≤11
y2+1>0
a≥3
(1)在汽车行驶的公路上,我们会看到不同的交通标志,它们有着不同的意义,如图所示,如果汽车的速度为V(km/h),你会用不等式表示图中标志的意义吗?
60
v≤60
(2)
若用t表示今天(11月23日)的气温,
则t的取值范围是
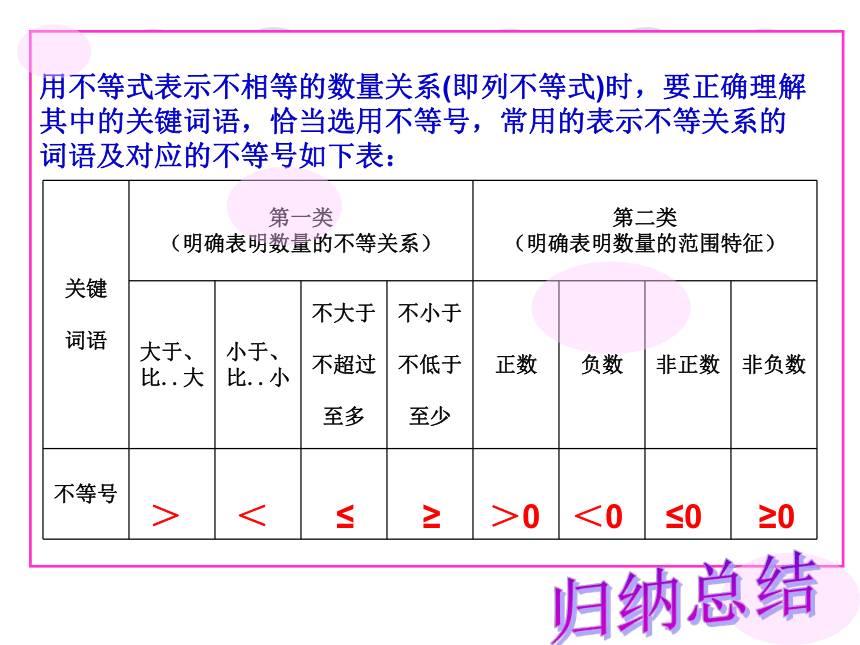
关键
词语
第一类
(明确表明数量的不等关系)
第二类
(明确表明数量的范围特征)
大于、
比..大
小于、
比..小
不大于
不超过
至多
不小于
不低于
至少
正数
负数
非正数
非负数
不等号
用不等式表示不相等的数量关系(即列不等式)时,要正确理解其中的关键词语,恰当选用不等号,常用的表示不等关系的词语及对应的不等号如下表:
>
<
≤
≥
>0
<0
≤0
≥0
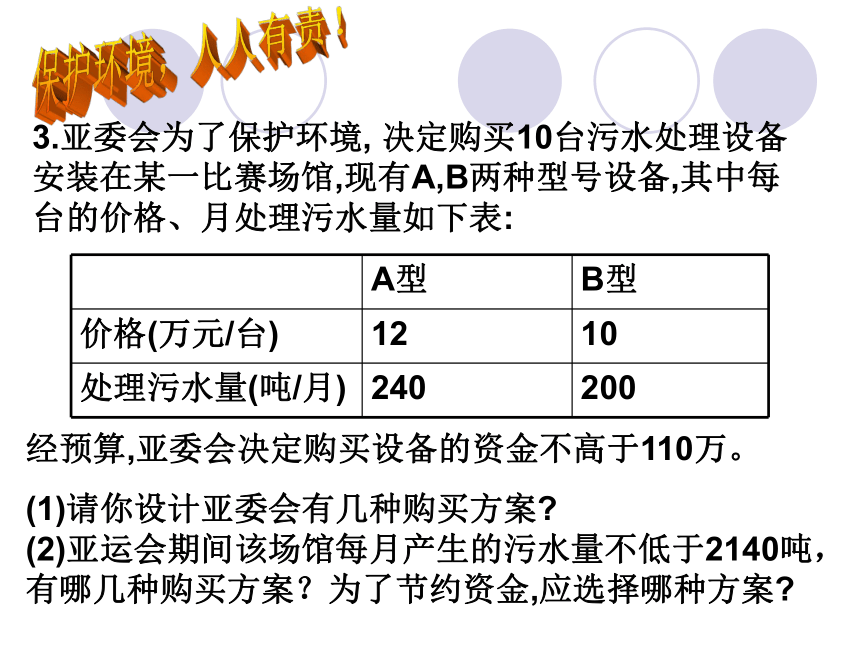
3.亚委会为了保护环境, 决定购买10台污水处理设备安装在某一比赛场馆,现有A,B两种型号设备,其中每台的价格、月处理污水量如下表:
A型
B型
价格(万元/台)
12
10
处理污水量(吨/月)
240
200
经预算,亚委会决定购买设备的资金不高于110万。
(1)请你设计亚委会有几种购买方案?
(2)亚运会期间该场馆每月产生的污水量不低于2140吨,有哪几种购买方案?为了节约资金,应选择哪种方案?
应用一元一次不等式(组)解决实际问题基本思路:
实际问题
数学问题
数学模型
一元一次不等式(组)
数学结论
抽象
求解
数学化
检验
这节课我们复习了哪些知识?
你有什么收获?
还有哪些疑惑?
1.已知关于x的不等式x+m>-5的解集如图所示,
则m的值为( )
A.1 B.0
C.-1 D.-2
3、已知不等式3x-m ≤0有4个正整数解,
则m的取值范围是 ,
2.关于x的不等式组{ 的解集是x>-1则m=__
x>m-1
x>m+2
D
-3
12≤m<15
4.为了抓住亚运会商机,某商店决定购进A、B两种亚运会纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
A 50元 B100元
1、求使不等式3(x-1)-1<2x成立的正整数解。
2、若不等式(a-2)x>a-2的解集为x<1,求a的取值范围( )。
A a < -2 B a < 2 C a >-2 D a >2
变式:已知不等式(a-2)x>3的解集为x< -1,则a的值是 。
B
-1
3.如果关于x的方程3x+a=x+4的解是个非负数,则a的取值范围________
a≤4
4.学校举办“环保知识” 竞赛,设一、二、三等奖共30名,用于购买奖品的总费用, 其中奖品单价及发放方案如下表:
奖项
一等奖
二等奖
三等奖
奖品
钢笔1支
文具盒1个
迷你便签本
单价(元)
50
30
18
若本次活动设一等奖5名,则二等奖可设多少名?
不超过800元,但又不少于750元
计时制:3元/小时.
包月制:60元/月,另加1元/小时.
什么情况下采用计时制合算,什么情况下采用包月制合算呢?你能用一元一次不等式解决这个问题吗
解:设每月上网x小时。
3x< 60+x
答: 若每月上网时间不足30小时则应该采用计时制,
若超过30小时则应采用包月制,
若等于30小时则两种收费制都可以.
计时制:3元/小时.
包月制:60元/月,另加1元/小时.
分析:按时上网的费用是:
按月上网的费用是:
3x >60+x
3x
60+x
3x =60+x
分类讨论:
某商品的零售价是每件50元,进价是每件35元。经核算,每天商店的各种费用(包括房租、售货员工资等)是120元,还需把商品售出价的10%上缴税款,问商店每天需要出售多少件这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
解:设商店每天出售该商品x件。根据题意得
(50-35-50×10%)x-120>100
解得
答:商店每天需要出售23件或23件以上这样的商品,才能保证商店每天获纯利润在100元以上。
即 10x>220
x>22
1、当 x________时,代数式
的值是非正数。
≥--
检测反馈:
2、如果方程2x-1=1的解是不等式
的一个解,则 a 的取值范围是_______
a<-1
3、如果关于x的方程3(x-4)=2a+x-18的解是个负数,若a是正整数,试确定x的值。
4.如果关于x的不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是___
A.a>0 B. a<0 C. a >-1 D. a<-1
5.如果不等式组 有解,则m的取值范围是___
A. m< B. m≤ C. m> D. m≥
6.我校因教学需要,准备刻录一批电脑光盘.若到电脑公司刻录,每张需8元,若租用刻录机后自行刻录,每张成本3.5元,但需付刻录机租金150元,设刻录的光盘数为x张,所需费用为y元,试讨论用何种方式费用较节省.
3-2x≥0
x≥m
谢谢各位领导和老师们的指导!
初中数学七年级下册
(苏科版)
③
______
⑥
⑧
①1>-3
②
④ 4+x
⑦
⑤
问题1解⑥号不等式 把解集在数轴表示出来,
问题2:归纳出解⑥不等式的具体步骤及每步的依据?
并求它的:正整数解
最大负整数解
①②③⑥⑦⑧
③⑥⑧
问题3:取③ ⑧ 再加⑨ x<4 ⑩ x>1
从中任取两个组合成不同的不等式组,并求它的解集(利用数轴或口诀)
含有1个未知数的不等式
含有一个未知数,不等号两边都为整式,且未知数次数为1次的不等式
叫一元一次不等式。
大于大的取最大,小于小的取最小,大小小大取中间,
大大小小则无解,如果有等号,等号跟着走 。
问题4:取⑥号
组成不等式组,求它的解集。
2、根据实际问题列出不等量关系
P≤11
y2+1>0
a≥3
(1)在汽车行驶的公路上,我们会看到不同的交通标志,它们有着不同的意义,如图所示,如果汽车的速度为V(km/h),你会用不等式表示图中标志的意义吗?
60
v≤60
(2)
若用t表示今天(11月23日)的气温,
则t的取值范围是
关键
词语
第一类
(明确表明数量的不等关系)
第二类
(明确表明数量的范围特征)
大于、
比..大
小于、
比..小
不大于
不超过
至多
不小于
不低于
至少
正数
负数
非正数
非负数
不等号
用不等式表示不相等的数量关系(即列不等式)时,要正确理解其中的关键词语,恰当选用不等号,常用的表示不等关系的词语及对应的不等号如下表:
>
<
≤
≥
>0
<0
≤0
≥0
3.亚委会为了保护环境, 决定购买10台污水处理设备安装在某一比赛场馆,现有A,B两种型号设备,其中每台的价格、月处理污水量如下表:
A型
B型
价格(万元/台)
12
10
处理污水量(吨/月)
240
200
经预算,亚委会决定购买设备的资金不高于110万。
(1)请你设计亚委会有几种购买方案?
(2)亚运会期间该场馆每月产生的污水量不低于2140吨,有哪几种购买方案?为了节约资金,应选择哪种方案?
应用一元一次不等式(组)解决实际问题基本思路:
实际问题
数学问题
数学模型
一元一次不等式(组)
数学结论
抽象
求解
数学化
检验
这节课我们复习了哪些知识?
你有什么收获?
还有哪些疑惑?
1.已知关于x的不等式x+m>-5的解集如图所示,
则m的值为( )
A.1 B.0
C.-1 D.-2
3、已知不等式3x-m ≤0有4个正整数解,
则m的取值范围是 ,
2.关于x的不等式组{ 的解集是x>-1则m=__
x>m-1
x>m+2
D
-3
12≤m<15
4.为了抓住亚运会商机,某商店决定购进A、B两种亚运会纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
A 50元 B100元
1、求使不等式3(x-1)-1<2x成立的正整数解。
2、若不等式(a-2)x>a-2的解集为x<1,求a的取值范围( )。
A a < -2 B a < 2 C a >-2 D a >2
变式:已知不等式(a-2)x>3的解集为x< -1,则a的值是 。
B
-1
3.如果关于x的方程3x+a=x+4的解是个非负数,则a的取值范围________
a≤4
4.学校举办“环保知识” 竞赛,设一、二、三等奖共30名,用于购买奖品的总费用, 其中奖品单价及发放方案如下表:
奖项
一等奖
二等奖
三等奖
奖品
钢笔1支
文具盒1个
迷你便签本
单价(元)
50
30
18
若本次活动设一等奖5名,则二等奖可设多少名?
不超过800元,但又不少于750元
计时制:3元/小时.
包月制:60元/月,另加1元/小时.
什么情况下采用计时制合算,什么情况下采用包月制合算呢?你能用一元一次不等式解决这个问题吗
解:设每月上网x小时。
3x< 60+x
答: 若每月上网时间不足30小时则应该采用计时制,
若超过30小时则应采用包月制,
若等于30小时则两种收费制都可以.
计时制:3元/小时.
包月制:60元/月,另加1元/小时.
分析:按时上网的费用是:
按月上网的费用是:
3x >60+x
3x
60+x
3x =60+x
分类讨论:
某商品的零售价是每件50元,进价是每件35元。经核算,每天商店的各种费用(包括房租、售货员工资等)是120元,还需把商品售出价的10%上缴税款,问商店每天需要出售多少件这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
解:设商店每天出售该商品x件。根据题意得
(50-35-50×10%)x-120>100
解得
答:商店每天需要出售23件或23件以上这样的商品,才能保证商店每天获纯利润在100元以上。
即 10x>220
x>22
1、当 x________时,代数式
的值是非正数。
≥--
检测反馈:
2、如果方程2x-1=1的解是不等式
的一个解,则 a 的取值范围是_______
a<-1
3、如果关于x的方程3(x-4)=2a+x-18的解是个负数,若a是正整数,试确定x的值。
4.如果关于x的不等式(a+1)x>a+1的解集为x<1,那么a的取值范围是___
A.a>0 B. a<0 C. a >-1 D. a<-1
5.如果不等式组 有解,则m的取值范围是___
A. m< B. m≤ C. m> D. m≥
6.我校因教学需要,准备刻录一批电脑光盘.若到电脑公司刻录,每张需8元,若租用刻录机后自行刻录,每张成本3.5元,但需付刻录机租金150元,设刻录的光盘数为x张,所需费用为y元,试讨论用何种方式费用较节省.
3-2x≥0
x≥m
谢谢各位领导和老师们的指导!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
