苏科版七年级下册数学课件 10.1二元一次方程(52张)
文档属性
| 名称 | 苏科版七年级下册数学课件 10.1二元一次方程(52张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 10:17:42 | ||
图片预览











文档简介
10.1 二元一次方程
揭
标
引
学
(1)经历分析实际问题中数量关系的过程,进一步体会方程是刻画现实世界的有效的数学模型.
(2)了解二元一次方程的概念,并会判断一组数是否是某个二元一次方程的解.
学习目标
情境1:如图,已知一个矩形的宽为3,周长为24,求矩形的长.如果我们设长为x,则可列方程为:______________.
x
3
y
2x+6=24
如果把问题中矩形的宽改为y,则可得到什么样的等量关系?
2x+2y=24
情
创
设
情
境
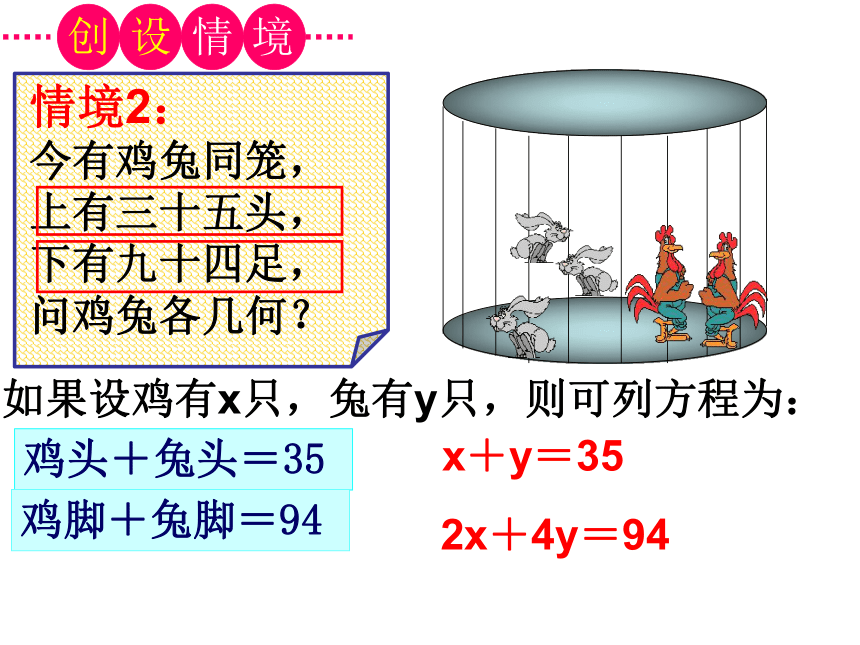
情境2:
今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何?
鸡头+兔头=35
鸡脚+兔脚=94
如果设鸡有x只,兔有y只,则可列方程为:
x+y=35
2x+4y=94
情
创
设
情
境
情境3:篮球比赛规则规定:赢一场得2分,输一场得1分.在中学生篮球联赛中,某球队赛了若干场,积20分.怎样描述该球队输、赢场数与积分之间的相等关系?
2x+y=20
问题2 如果设该队赢了x场,输了y场.
问题1 问题中存在哪些相等关系?
赢的场数×2+输的场数×1=20
问题3 你能列出输赢的所有可能情况吗?
x
5
y
10
20
0
1
2
3
4
6
7
8
9
10
18
16
14
12
8
6
4
2
0
情
创
设
情
境
情境4:某球员在一场篮球比赛中共得35分(其中罚球得10分).问:他分别投中了多少个两分球和三分球?
两分球得分+三分球得分+罚球得分=35
设他投中了x个两分球、y个三分球
2x+3y+10=35
你能列出输赢的所有可能情况吗?
x
y
1
11
8
5
2
3
5
7
2x+3y=25
情
创
设
情
境
议一议
观察以下方程,它们有哪些共同特点?
2x+2y=24 x+y=35
2x+4y=94 2x+y=20
2x+3y+10=35
1.含有两个未知数;
2.含未知数的项的次数是1次;
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
含有两个未知数,并且所含未知数的项的次数都是1的整式方程叫做二元一次方程.
1、二元一次方程的定义:
梳
理
知
识
二元一次方程的特征:
1.首先必须是一个等式;
2.含有两个未知数;
3.含未知数的项的次数是1次;
4.左右两边都是整式.
1、下列方程中,哪些是二元一次方程?
(1)3x+2y+3 (2)2x-3y+4=0
(3)x+3y-2z=4 (4)x2-y2=1
(5)5+3y=4x+3y (6)
(7) (8)3ab=1
×
试一试
√
×
×
×
√
×
×
2x+y=20
x
5
y
10
20
0
1
2
3
4
6
7
8
9
10
18
16
14
12
8
6
4
2
0
2x+3y+10=35
x
y
1
11
8
5
2
3
5
7
梳
理
知
识
适合二元一次方程的一对未知数的值,叫二元一次方程的一个解.
解的表示方法:记为 的形式.
适合二元一次方程的一对未知数的值,叫二元一次方程的一个解.
剖析:
①任何一个二元一次方程都有无数个解;
②解的表示方法:二元一次方程(未知数为x、
2、二元一次方程的解:
梳
理
知
识
y)的每一个解都是一对数表示为 的形式.
2、下面3对数值,哪几对是二元一次方程2x+y=3的解?哪几对是二元一次方程
3x+4y=2的解?
试一试
2x+y=3
2x+y=3
3x+4y=2
3x+4y=2
例1 下列各式:
①x-3y=1; ② ;③y-z=4;
④xy=4;⑤5x-3y;⑥ ;
⑦x+y+z
=6; ⑧x+3y=x+2,
其中属于二元一次方程的有( )
A、1个 B、2个 C、3个 D、4个
注:二元一次方程的的识别注意以下几点:
①二元:含有两个未知数
②一次:含未知数的项的次数是1次
③整式方程:方程中的每一项都应是整式
例
题
讲
解
例2?? 甲种物品每个4kg,乙种物品每个7kg.现有甲种物品x个,乙种物品y个,共76kg .
(1)列出关于x、y的二元一次方程;
(2)如果x=12,求y的值;
(3)请将关于x、y的二元一次方程写成用含x的代数式表示y的形式
小结:二元一次方程中,用一个字母的代数式表示另一个字母,即把这个字母看成已知数,把另一个字母看成未知数.
例
题
讲
解
练一练
把下列方程写成用含y的代数式表示x的形式,并写出这个方程的一个解.
(1)x+3y=7 (2)4x+3y=32
(3)5x+y=15 (4)3x-4y=12
例
题
讲
解
例3 已知 是方程2x+3y=5的一个解,求a的值.
解: 把x=-2,y=a代入方程2x+3y=5,得:
2×(-2)+3×a=5
∴ 3a=9
∴ a=3
1、下列方程中,属于二元一次方程的是( )
C、m-n=30 D、2xy-1=0
2、下列各组数值中是方程x-2y=4的解的是( )
A、-2a=3a+1 B、
A、 B、 C、 D、
课
堂
反
馈
3、二元一次方程5a-11b=21( )
A、有且只有一解 B、有无数解
C、无解 D、有且只有两解
4、由 可以得到用x表示y的式子是( )
A、 B、
C、 D、
课
堂
反
馈
6、已知 是关于x、y的二元一次方程
ax-(2a-3)y=7的解,求a的值.
5、已知 是的二元一次方程3x-ky=2的
一个解,则k=___.
课
堂
反
馈
7、某公园的门票价格为:成人票8元/张,儿童票3元/张.现在x名成人,y名儿童,买门票共花了44元.列出关于x、y的方程.
8、盒子里有若干个大小相同的白球和红球,从中摸到1个红球得2分.摸到1个白球得3分.某人摸到x个红球,y个白球,共得12分.列出关于x、y的方程.
课
堂
反
馈
1、二元一次方程的的识别注意以下几点:
①二元:含有两个未知数
②一次:含未知数的项的次数是1次
③整式方程:方程中的每一项都应是整式
课
堂
总结
结
定义
一般形式
解的个数
解的
表示
一元一次方程
只含有一个未知数且未知数的指数是1
ax+b=c
(a≠0)
唯一
x=a
二元一次方程
含有两个未知数,并且所含有未知数的项的次数都是1的方程
ax+by+c=0
(a≠0,b≠0)
无数
2、二元一次方程与一元一次方程的异同点
课
堂
总结
结
1、已知二元一次方程2(x-3)= -3(y+1)+2
①用含x的代数式表示y.
②用含y的代数式表示x.
③求此方程的所有自然数解.
2、若方程(m-1)xn+(n-2)y|m|=0是关于x、y的二元一次方程,则m=__,n=__.
拓
展
延
伸
已知二元一次方程 3x+2y=10.
(1) 用关于x的代数式表示y;
(2) 求当x= -2,0,3时,对应的y的值,
并写出方程3x+2y=10的三个解.
3、设有1角的硬币x枚,5角的硬币y枚,硬币的总值4元
(1)可以列出方程:_____
(2)如果全是1角的硬币,共有多少枚?如果全是5角的硬币共有多少枚?
(3)用列表格的方式,列出1角和5角硬币枚数所有的可能情况.
自
学
检
查
x+5y=40
x
40
35
30
25
20
15
10
5
0
y
0
1
2
3
4
5
6
7
8
1、已知二元一次方程2(x-3)= -3(y+1)+2
①用含x的代数式表示y.
②用含y的代数式表示x.
③求此方程的所有自然数解.
2、若方程(m-1)xn+(n-2)y|m|=0是关于x、y的二元一次方程,则m=__,n=__.
拓
展
延
伸
3、若方程(m—1)xn+(n—2)y︱m︳=0是
关于x、y的二元一次方程,则m=_,n=_.
拓
展
延
伸
问题1:
如图,已知一个矩形的宽为3,周长为24,求矩形的长.如果我们设长为x,则可列方程为:_________________.
如果把问题中矩形的宽改为y,则可得到什么样的等量关系?
3
x+3=12
x+y=12
x
y
今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何?
鸡头+兔头=35
鸡脚+兔脚=94
如果设鸡有x只,兔有y只,
则可列方程为:
x+y=35
2x+4y=94
问题2:
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,比赛了若干场后积20分,问该球队赢了多少场?输了多少场?
想一想:
问题3:
如果设该队赢了x场,输了y场,那么:
2x+y=20
x+y=12, x+y=35 ,
2x+4y=94, 2x+y=20
请找出下列方程的共同特点:
含有两个未知数,
叫做二元一次方程.
且含有未知
数的项的次数都是一次的方程
判断下列式子是否为二元一次方程?
(1) 3x+1=x2
(5) xy+y=2
(3) x=―+1
2
y
(6) -2y=0
3
x
(2) x2+y=0
(4) y+―x
2
1
不是
不是
不是
不是
不是
是
练一练
含有两个未知数,且含有未知数的项的次数都是一次的方程
(1)已知:5xm+7-2y2n-1=4是二元一次方程,mn= .
考考你
-6
(2)、根据下列语句, 列出二元一次方程:
1.甲数比乙数大3.设甲数为x,乙数为y;
2.一个长方形的周长是20cm.设这个长方形的长是xcm,宽是ycm;
3.甲、乙两人各工作5天,共生产零件80件.设甲每天生产零件x件,乙每天生产零件y件.
你能编拟一个所列方程为:2x+y=5
的实际问题吗?
x+3=12
使一元一次方程两边的值相等的未知数的值叫做一元一次方程的解.
使二元一次方程两边的值相等的一对未知数的值叫做二元一次方程的一个解.
想一想
是方程 的一个解。
x=0
y=5
3x+2y=10
下列各对数哪几对是二元一次方程
3x+2y=10的解?
把 代入方程3x+2y=10中,得
左边=3 2+2 2=10=右边.所以
是二元一次方程的一个解。
x=2
y=2
x=2
y=2
x=2
y=2
x=3
y=1
x=
y=4
(1)、你能写出二元一次方程
2x+y=5的解吗?
一个二元一次方程有无数个解;以一组未知数的值为解的二元一次方程也有无数个。
看谁写的快,写得多!
看谁理解好
试一试
(2)、请写出一个以 为解的二元一次方程.
x=2
y=1
x
y
0
20
1
18
2
16
3
14
4
12
5
10
6
7
8
9
10
8
6
4
2
0
动动脑筋?你能列出输赢的所有可能情况吗?
该队赢了x场,输了y场,那么
2x+y=20
已知二元一次方程 3x+y=10.
(1)用关于y的代数式表示x.
解:移项,得3x =10 -y
x =
10- y
3
所以
(2)用关于x的代数式表示y.
变式训练
(3) 求当x= -2,0,3时,对应的y的值, 并写出方程3x+y=10的三个解.
甲种铅笔每枝0.2元,乙种铅笔每枝0.5元,现在某人买了x枝甲种铅笔,y枝乙种铅笔,共花了7元.
(1)列出关于x,y的二元一次方程.
(2)如果x=5,那么y的值是多少?
(3)如果乙种铅笔买了10枝,那么甲种铅笔买了多少枝?
考考你
议一议:
类比一元一次方程:
2x+y=20和2x+3y=25是什么方程?它们有哪些共同的特点?
判断下列式子是否为二元一次方程?
(1) 3x+1=x2
(5) xy+y=2
(3) x=―+1
2
y
(6) -2y=0
3
x
(2) x2+y=0
(4) y+―x
2
1
不是
不是
不是
不是
不是
是
适合二元一次方程的一对未知数的值称为这个二元一次方程的一个解。
记作:
你能写出二元一次方程2x+y=5的所有解吗?
由此你可以得出什么结论?
x、y取何值时,能使2x+3y=25 成立?
例2 把下列方程写成用含x的代数式表示y的形式,并写出这个方程的一个解.
(1)5x+y=15 (2)3x-4y=12
小结:二元一次方程中,用一个字母的代数式表示另一个字母,即把这个字母看成已知数,把另一个字母看成未知数.
例题讲解
例1、下列方程中,哪些是二元一次方程?不是的说明理由.
(3)3pq=-8
(4)2y2-6y=1
(5)5(x-y)+2(2x-3y)=4
(6)7x+2=3
【例1】下列方程中,哪些是二元一次方程?不是的说明理由.
(3)3pq=-8; (4)2y2-6y=1;
(5)5(x-y)+2(2x-3y)=4;
(6)7x+2=3.
【例2】把下列方程写成用含x的代数式表示y的形式.
2x+y=20; 2x+3y=25.
变式:用含y的代数式表示x.
10.1 二元一次方程
【能力检测】
已知二元一次方程 3x+2y=10.
(1)用关于x的代数式表示y;
(2)求当x=-2,0,3时,对应的y的值,并写出方程3x+2y=10的三个解.
10.1 二元一次方程
4、甲种铅笔每枝0.2元,乙种铅笔每枝0.5元,现在某人买了x枝甲种铅笔,y枝乙种铅笔,共花了7元.
(1)列出关于x,y的二元一次方程.
(2)如果x=5,那么y的值是多少?
(3)如果乙种铅笔买了10枝,那么甲种铅笔买了多少枝?
(1)已知:5xm+7-2y2n-1=4是二元一次方程,mn= .
(2)若mxy+9x+3yn-1=7是关于x,y的二元一次方程,则m+n= .
考考你
-6
2
根据下列语句,分别设适当的未知数,列出二元一次方程:
1.甲数比乙数大3.设甲数为x,乙数为y;
2.一个长方形的周长是20cm.设这个长方形的长是xcm,宽是ycm;
3.甲、乙两人各工作5天,共生产零件80件.设甲每天生产零件x件,乙每天生产零件y件.
揭
标
引
学
(1)经历分析实际问题中数量关系的过程,进一步体会方程是刻画现实世界的有效的数学模型.
(2)了解二元一次方程的概念,并会判断一组数是否是某个二元一次方程的解.
学习目标
情境1:如图,已知一个矩形的宽为3,周长为24,求矩形的长.如果我们设长为x,则可列方程为:______________.
x
3
y
2x+6=24
如果把问题中矩形的宽改为y,则可得到什么样的等量关系?
2x+2y=24
情
创
设
情
境
情境2:
今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何?
鸡头+兔头=35
鸡脚+兔脚=94
如果设鸡有x只,兔有y只,则可列方程为:
x+y=35
2x+4y=94
情
创
设
情
境
情境3:篮球比赛规则规定:赢一场得2分,输一场得1分.在中学生篮球联赛中,某球队赛了若干场,积20分.怎样描述该球队输、赢场数与积分之间的相等关系?
2x+y=20
问题2 如果设该队赢了x场,输了y场.
问题1 问题中存在哪些相等关系?
赢的场数×2+输的场数×1=20
问题3 你能列出输赢的所有可能情况吗?
x
5
y
10
20
0
1
2
3
4
6
7
8
9
10
18
16
14
12
8
6
4
2
0
情
创
设
情
境
情境4:某球员在一场篮球比赛中共得35分(其中罚球得10分).问:他分别投中了多少个两分球和三分球?
两分球得分+三分球得分+罚球得分=35
设他投中了x个两分球、y个三分球
2x+3y+10=35
你能列出输赢的所有可能情况吗?
x
y
1
11
8
5
2
3
5
7
2x+3y=25
情
创
设
情
境
议一议
观察以下方程,它们有哪些共同特点?
2x+2y=24 x+y=35
2x+4y=94 2x+y=20
2x+3y+10=35
1.含有两个未知数;
2.含未知数的项的次数是1次;
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
含有两个未知数,并且所含未知数的项的次数都是1的整式方程叫做二元一次方程.
1、二元一次方程的定义:
梳
理
知
识
二元一次方程的特征:
1.首先必须是一个等式;
2.含有两个未知数;
3.含未知数的项的次数是1次;
4.左右两边都是整式.
1、下列方程中,哪些是二元一次方程?
(1)3x+2y+3 (2)2x-3y+4=0
(3)x+3y-2z=4 (4)x2-y2=1
(5)5+3y=4x+3y (6)
(7) (8)3ab=1
×
试一试
√
×
×
×
√
×
×
2x+y=20
x
5
y
10
20
0
1
2
3
4
6
7
8
9
10
18
16
14
12
8
6
4
2
0
2x+3y+10=35
x
y
1
11
8
5
2
3
5
7
梳
理
知
识
适合二元一次方程的一对未知数的值,叫二元一次方程的一个解.
解的表示方法:记为 的形式.
适合二元一次方程的一对未知数的值,叫二元一次方程的一个解.
剖析:
①任何一个二元一次方程都有无数个解;
②解的表示方法:二元一次方程(未知数为x、
2、二元一次方程的解:
梳
理
知
识
y)的每一个解都是一对数表示为 的形式.
2、下面3对数值,哪几对是二元一次方程2x+y=3的解?哪几对是二元一次方程
3x+4y=2的解?
试一试
2x+y=3
2x+y=3
3x+4y=2
3x+4y=2
例1 下列各式:
①x-3y=1; ② ;③y-z=4;
④xy=4;⑤5x-3y;⑥ ;
⑦x+y+z
=6; ⑧x+3y=x+2,
其中属于二元一次方程的有( )
A、1个 B、2个 C、3个 D、4个
注:二元一次方程的的识别注意以下几点:
①二元:含有两个未知数
②一次:含未知数的项的次数是1次
③整式方程:方程中的每一项都应是整式
例
题
讲
解
例2?? 甲种物品每个4kg,乙种物品每个7kg.现有甲种物品x个,乙种物品y个,共76kg .
(1)列出关于x、y的二元一次方程;
(2)如果x=12,求y的值;
(3)请将关于x、y的二元一次方程写成用含x的代数式表示y的形式
小结:二元一次方程中,用一个字母的代数式表示另一个字母,即把这个字母看成已知数,把另一个字母看成未知数.
例
题
讲
解
练一练
把下列方程写成用含y的代数式表示x的形式,并写出这个方程的一个解.
(1)x+3y=7 (2)4x+3y=32
(3)5x+y=15 (4)3x-4y=12
例
题
讲
解
例3 已知 是方程2x+3y=5的一个解,求a的值.
解: 把x=-2,y=a代入方程2x+3y=5,得:
2×(-2)+3×a=5
∴ 3a=9
∴ a=3
1、下列方程中,属于二元一次方程的是( )
C、m-n=30 D、2xy-1=0
2、下列各组数值中是方程x-2y=4的解的是( )
A、-2a=3a+1 B、
A、 B、 C、 D、
课
堂
反
馈
3、二元一次方程5a-11b=21( )
A、有且只有一解 B、有无数解
C、无解 D、有且只有两解
4、由 可以得到用x表示y的式子是( )
A、 B、
C、 D、
课
堂
反
馈
6、已知 是关于x、y的二元一次方程
ax-(2a-3)y=7的解,求a的值.
5、已知 是的二元一次方程3x-ky=2的
一个解,则k=___.
课
堂
反
馈
7、某公园的门票价格为:成人票8元/张,儿童票3元/张.现在x名成人,y名儿童,买门票共花了44元.列出关于x、y的方程.
8、盒子里有若干个大小相同的白球和红球,从中摸到1个红球得2分.摸到1个白球得3分.某人摸到x个红球,y个白球,共得12分.列出关于x、y的方程.
课
堂
反
馈
1、二元一次方程的的识别注意以下几点:
①二元:含有两个未知数
②一次:含未知数的项的次数是1次
③整式方程:方程中的每一项都应是整式
课
堂
总结
结
定义
一般形式
解的个数
解的
表示
一元一次方程
只含有一个未知数且未知数的指数是1
ax+b=c
(a≠0)
唯一
x=a
二元一次方程
含有两个未知数,并且所含有未知数的项的次数都是1的方程
ax+by+c=0
(a≠0,b≠0)
无数
2、二元一次方程与一元一次方程的异同点
课
堂
总结
结
1、已知二元一次方程2(x-3)= -3(y+1)+2
①用含x的代数式表示y.
②用含y的代数式表示x.
③求此方程的所有自然数解.
2、若方程(m-1)xn+(n-2)y|m|=0是关于x、y的二元一次方程,则m=__,n=__.
拓
展
延
伸
已知二元一次方程 3x+2y=10.
(1) 用关于x的代数式表示y;
(2) 求当x= -2,0,3时,对应的y的值,
并写出方程3x+2y=10的三个解.
3、设有1角的硬币x枚,5角的硬币y枚,硬币的总值4元
(1)可以列出方程:_____
(2)如果全是1角的硬币,共有多少枚?如果全是5角的硬币共有多少枚?
(3)用列表格的方式,列出1角和5角硬币枚数所有的可能情况.
自
学
检
查
x+5y=40
x
40
35
30
25
20
15
10
5
0
y
0
1
2
3
4
5
6
7
8
1、已知二元一次方程2(x-3)= -3(y+1)+2
①用含x的代数式表示y.
②用含y的代数式表示x.
③求此方程的所有自然数解.
2、若方程(m-1)xn+(n-2)y|m|=0是关于x、y的二元一次方程,则m=__,n=__.
拓
展
延
伸
3、若方程(m—1)xn+(n—2)y︱m︳=0是
关于x、y的二元一次方程,则m=_,n=_.
拓
展
延
伸
问题1:
如图,已知一个矩形的宽为3,周长为24,求矩形的长.如果我们设长为x,则可列方程为:_________________.
如果把问题中矩形的宽改为y,则可得到什么样的等量关系?
3
x+3=12
x+y=12
x
y
今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何?
鸡头+兔头=35
鸡脚+兔脚=94
如果设鸡有x只,兔有y只,
则可列方程为:
x+y=35
2x+4y=94
问题2:
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,比赛了若干场后积20分,问该球队赢了多少场?输了多少场?
想一想:
问题3:
如果设该队赢了x场,输了y场,那么:
2x+y=20
x+y=12, x+y=35 ,
2x+4y=94, 2x+y=20
请找出下列方程的共同特点:
含有两个未知数,
叫做二元一次方程.
且含有未知
数的项的次数都是一次的方程
判断下列式子是否为二元一次方程?
(1) 3x+1=x2
(5) xy+y=2
(3) x=―+1
2
y
(6) -2y=0
3
x
(2) x2+y=0
(4) y+―x
2
1
不是
不是
不是
不是
不是
是
练一练
含有两个未知数,且含有未知数的项的次数都是一次的方程
(1)已知:5xm+7-2y2n-1=4是二元一次方程,mn= .
考考你
-6
(2)、根据下列语句, 列出二元一次方程:
1.甲数比乙数大3.设甲数为x,乙数为y;
2.一个长方形的周长是20cm.设这个长方形的长是xcm,宽是ycm;
3.甲、乙两人各工作5天,共生产零件80件.设甲每天生产零件x件,乙每天生产零件y件.
你能编拟一个所列方程为:2x+y=5
的实际问题吗?
x+3=12
使一元一次方程两边的值相等的未知数的值叫做一元一次方程的解.
使二元一次方程两边的值相等的一对未知数的值叫做二元一次方程的一个解.
想一想
是方程 的一个解。
x=0
y=5
3x+2y=10
下列各对数哪几对是二元一次方程
3x+2y=10的解?
把 代入方程3x+2y=10中,得
左边=3 2+2 2=10=右边.所以
是二元一次方程的一个解。
x=2
y=2
x=2
y=2
x=2
y=2
x=3
y=1
x=
y=4
(1)、你能写出二元一次方程
2x+y=5的解吗?
一个二元一次方程有无数个解;以一组未知数的值为解的二元一次方程也有无数个。
看谁写的快,写得多!
看谁理解好
试一试
(2)、请写出一个以 为解的二元一次方程.
x=2
y=1
x
y
0
20
1
18
2
16
3
14
4
12
5
10
6
7
8
9
10
8
6
4
2
0
动动脑筋?你能列出输赢的所有可能情况吗?
该队赢了x场,输了y场,那么
2x+y=20
已知二元一次方程 3x+y=10.
(1)用关于y的代数式表示x.
解:移项,得3x =10 -y
x =
10- y
3
所以
(2)用关于x的代数式表示y.
变式训练
(3) 求当x= -2,0,3时,对应的y的值, 并写出方程3x+y=10的三个解.
甲种铅笔每枝0.2元,乙种铅笔每枝0.5元,现在某人买了x枝甲种铅笔,y枝乙种铅笔,共花了7元.
(1)列出关于x,y的二元一次方程.
(2)如果x=5,那么y的值是多少?
(3)如果乙种铅笔买了10枝,那么甲种铅笔买了多少枝?
考考你
议一议:
类比一元一次方程:
2x+y=20和2x+3y=25是什么方程?它们有哪些共同的特点?
判断下列式子是否为二元一次方程?
(1) 3x+1=x2
(5) xy+y=2
(3) x=―+1
2
y
(6) -2y=0
3
x
(2) x2+y=0
(4) y+―x
2
1
不是
不是
不是
不是
不是
是
适合二元一次方程的一对未知数的值称为这个二元一次方程的一个解。
记作:
你能写出二元一次方程2x+y=5的所有解吗?
由此你可以得出什么结论?
x、y取何值时,能使2x+3y=25 成立?
例2 把下列方程写成用含x的代数式表示y的形式,并写出这个方程的一个解.
(1)5x+y=15 (2)3x-4y=12
小结:二元一次方程中,用一个字母的代数式表示另一个字母,即把这个字母看成已知数,把另一个字母看成未知数.
例题讲解
例1、下列方程中,哪些是二元一次方程?不是的说明理由.
(3)3pq=-8
(4)2y2-6y=1
(5)5(x-y)+2(2x-3y)=4
(6)7x+2=3
【例1】下列方程中,哪些是二元一次方程?不是的说明理由.
(3)3pq=-8; (4)2y2-6y=1;
(5)5(x-y)+2(2x-3y)=4;
(6)7x+2=3.
【例2】把下列方程写成用含x的代数式表示y的形式.
2x+y=20; 2x+3y=25.
变式:用含y的代数式表示x.
10.1 二元一次方程
【能力检测】
已知二元一次方程 3x+2y=10.
(1)用关于x的代数式表示y;
(2)求当x=-2,0,3时,对应的y的值,并写出方程3x+2y=10的三个解.
10.1 二元一次方程
4、甲种铅笔每枝0.2元,乙种铅笔每枝0.5元,现在某人买了x枝甲种铅笔,y枝乙种铅笔,共花了7元.
(1)列出关于x,y的二元一次方程.
(2)如果x=5,那么y的值是多少?
(3)如果乙种铅笔买了10枝,那么甲种铅笔买了多少枝?
(1)已知:5xm+7-2y2n-1=4是二元一次方程,mn= .
(2)若mxy+9x+3yn-1=7是关于x,y的二元一次方程,则m+n= .
考考你
-6
2
根据下列语句,分别设适当的未知数,列出二元一次方程:
1.甲数比乙数大3.设甲数为x,乙数为y;
2.一个长方形的周长是20cm.设这个长方形的长是xcm,宽是ycm;
3.甲、乙两人各工作5天,共生产零件80件.设甲每天生产零件x件,乙每天生产零件y件.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
