第三章 圆单元质量检测试卷A(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版2020-20201年九年级(下)第三章圆检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
已知圆的半径为
,这个圆的内接正六边形的面积为
A.
B.
C.
D.
2.
下列图形中对称轴最多的是
A.
等边三角形
B.
线段
C.
正方形
D.
圆
3.
如图,
中,,,
与
的三边相切于点
,,,若
的半径为
,则
的周长为
A.
B.
C.
D.
4.
如图,点
,,
在同一条直线上,点
在直线外,过这四点中的任意
个点,能画圆的个数是
A.
B.
C.
D.
5.
下列说法错误的是
A.
直径是圆中最长的弦
B.
长度相等的两条弧是等弧
C.
面积相等的两个圆是等圆
D.
半径相等的两个半圆是等弧
6.
已知
的半径为
,圆心
到直线
的距离为
,则正确反映直线
与
的位置关系的图形是
A.
B.
C.
D.
7.
在平面直角坐标系中,
点的坐标为
,以
为半径画
,则以下结论正确的是
A.
与
轴相交,与
轴相切
B.
与
轴相切,与
轴相离
C.
与
轴相离,与
轴相交
D.
与
轴相离,与
轴相切
8.
如果两圆的半径分别是
,,圆心距为
,那么两圆的位置关系是
A.
外切
B.
相交
C.
内切
D.
内含
9.
下列选项中,直线一定是圆的切线的是
A.
与圆有公共点的直线
B.
到圆心的距离等于半径的直线
C.
垂直于圆的半径的直线
D.
过圆的直径的端点的直线
10.
如图,等边三角形
的边长为
,以
上一点
为圆心的圆分别与边
,
相切,则
的半径为
A.
B.
C.
D.
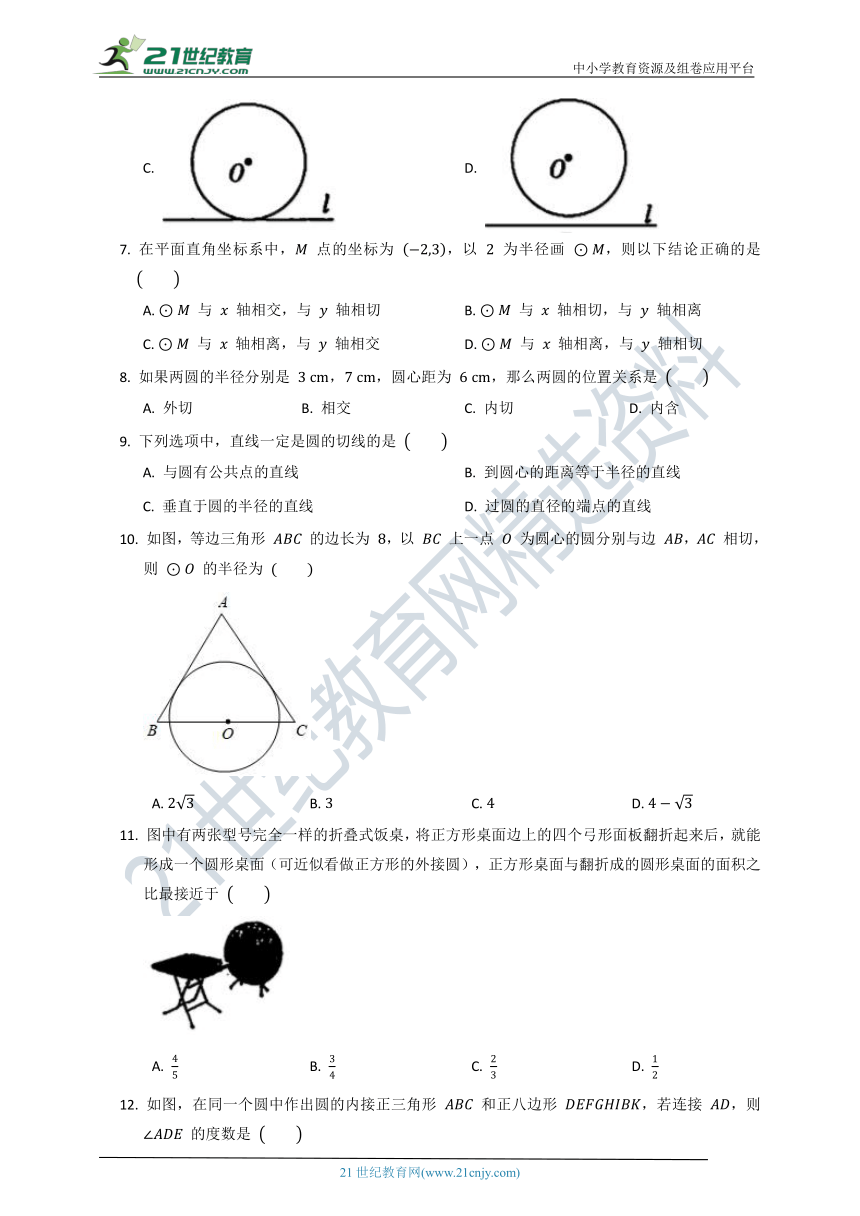
11.
图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看做正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近于
A.
B.
C.
D.
12.
如图,在同一个圆中作出圆的内接正三角形
和正八边形
,若连接
,则
的度数是
A.
B.
C.
D.
二、填空题(共6小题;每小题4分,共24
分)
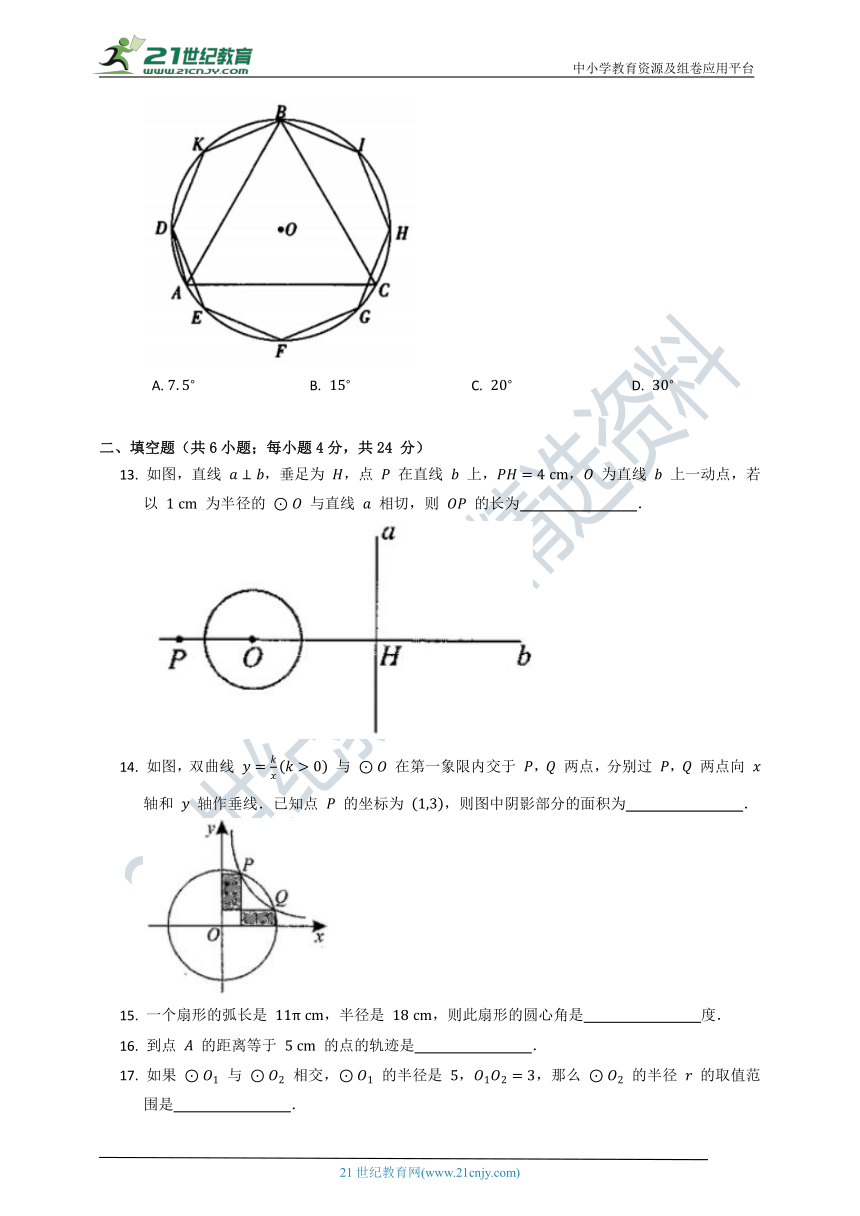
13.
如图,直线
,垂足为
,点
在直线
上,,
为直线
上一动点,若以
为半径的
与直线
相切,则
的长为
?.
14.
如图,双曲线
与
在第一象限内交于
,
两点,分别过
,
两点向
轴和
轴作垂线.已知点
的坐标为
,则图中阴影部分的面积为
?.
15.
一个扇形的弧长是
,半径是
,则此扇形的圆心角是
?度.
16.
到点
的距离等于
的点的轨迹是
?.
17.
如果
与
相交,
的半径是
,,那么
的半径
的取值范围是
?.
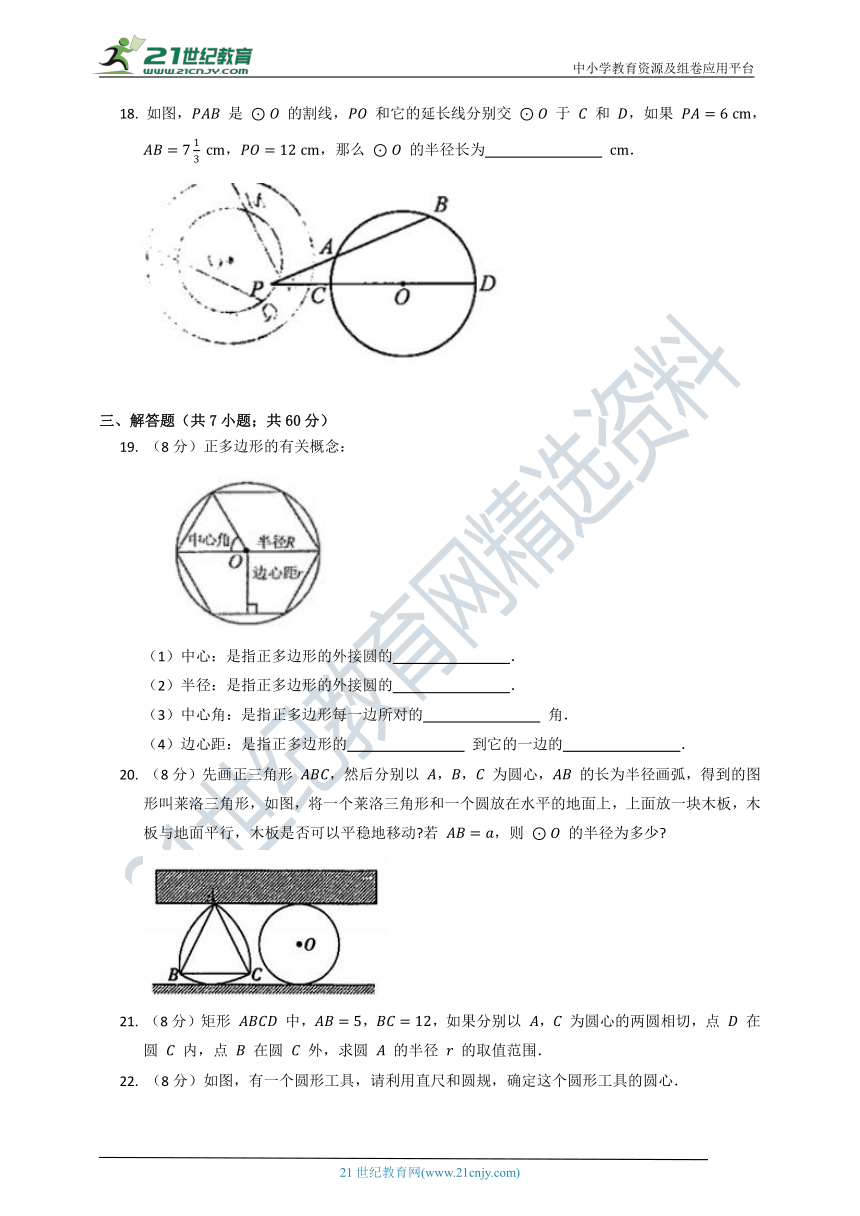
18.
如图,
是
的割线,
和它的延长线分别交
于
和
,如果
,,,那么
的半径长为
?
.
三、解答题(共7小题;共60分)
19.
(8分)正多边形的有关概念:
(1)中心:是指正多边形的外接圆的
?.
(2)半径:是指正多边形的外接圆的
?.
(3)中心角:是指正多边形每一边所对的
?
角.
(4)边心距:是指正多边形的
?
到它的一边的
?.
20.
(8分)先画正三角形
,然后分别以
,,
为圆心,
的长为半径画弧,得到的图形叫莱洛三角形,如图,将一个莱洛三角形和一个圆放在水平的地面上,上面放一块木板,木板与地面平行,木板是否可以平稳地移动?若
,则
的半径为多少?
21.
(8分)矩形
中,,,如果分别以
,
为圆心的两圆相切,点
在圆
内,点
在圆
外,求圆
的半径
的取值范围.
22.
(8分)如图,有一个圆形工具,请利用直尺和圆规,确定这个圆形工具的圆心.
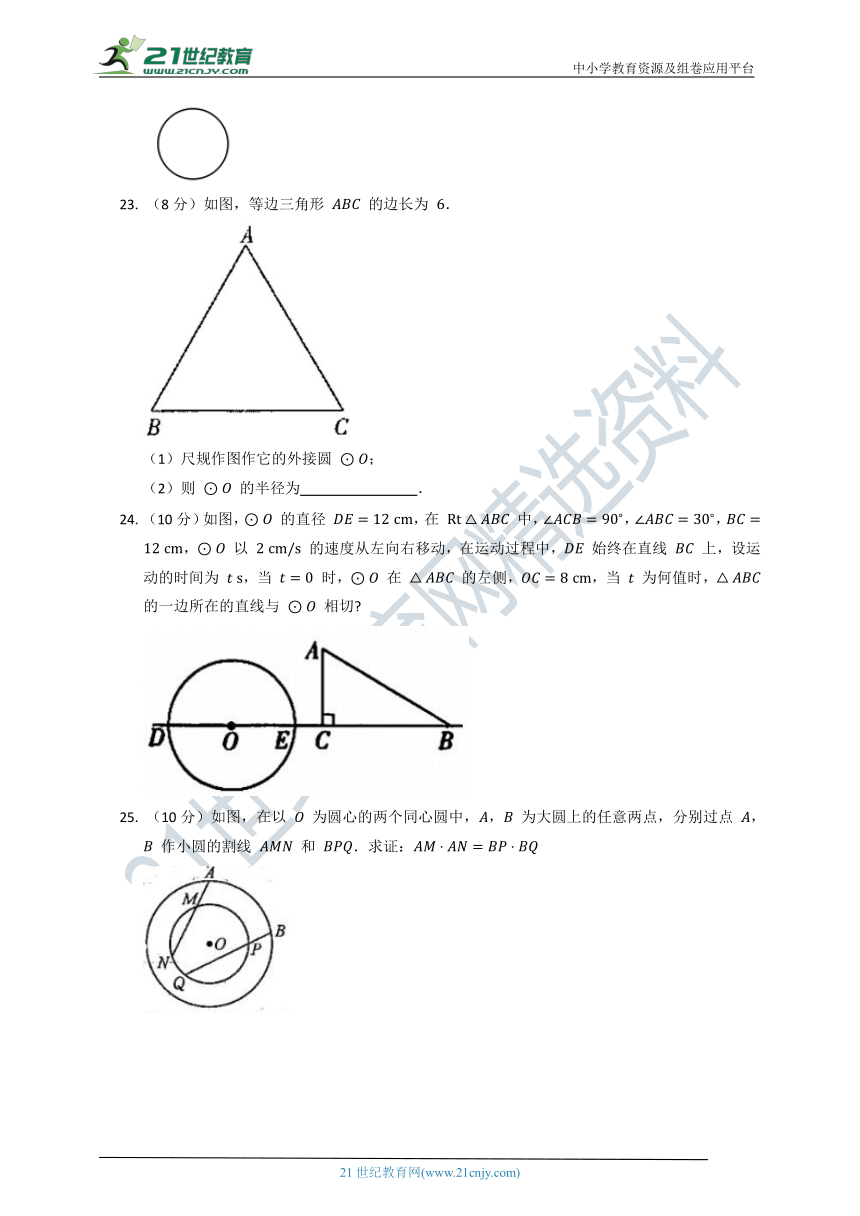
23.
(8分)如图,等边三角形
的边长为
.
(1)尺规作图作它的外接圆
;
(2)则
的半径为
?.
24.
(10分)如图,
的直径
,在
中,,,,
以
的速度从左向右移动,在运动过程中,
始终在直线
上,设运动的时间为
,当
时,
在
的左侧,,当
为何值时,
的一边所在的直线与
相切?
25.
(10分)如图,在以
为圆心的两个同心圆中,,
为大圆上的任意两点,分别过点
,
作小圆的割线
和
.求证:
答案
第一部分
1.
B
【解析】如图,连接
,,作
,
六边形
是正六边形,
,
,
,
是等边三角形,
,
则
,
2.
D
3.
D
4.
C
【解析】从
,,
三点中任取两点,有
种情况,这
种情况中的每一种情况都与点
构成不在同一直线上的三点,故能画出
个圆.
5.
B
【解析】直径是圆中最长的弦,所以A选项的说法正确;
在同圆或等圆中,长度相等的两条弧是等弧,所以B选项的说法错误;
面积相等的两个圆的半径相等,则它们是等圆,所以C选项的说法正确;
半径相等的两个半圆是等弧,所以D选项的说法正确.
6.
B
【解析】因为圆心
到直线
的距离小于圆的半径且不为
,所以直线
与圆相交且不过圆心.
7.
D
【解析】
点的坐标为
,
点
到
轴的距离为
,到
轴的距离为
,
的半径为
,
圆心
到
轴的距离大于半径,到
轴的距离等于半径,
故
与
轴相离,与
轴相切.
8.
B
9.
B
【解析】与圆只有一个公共点的直线是圆的切线,故A项不符合题意;圆的切线垂直于圆的半径且经过半径的外端,故C项不符合题意;过圆的直径的端点且与该直径垂直的直线是圆的切线,故D项不符合题意.故选B.
10.
A
【解析】设
,
上的切点为
,,由切割线定理可得:
,,,
,
,,,
由勾股定理可得
.
11.
C
【解析】如图,连接
,
设正方形的边长为
,
四边形
是正方形,
,
为圆的直径,
,
则正方形桌面与翻折成的圆形桌面的面积之比为
,故选C.
12.
A
【解析】如图,连接
,,,.
正三角形的中心角
,
正八边形的中心角
,
,
,
.
第二部分
13.
或
14.
15.
【解析】设这个扇形的圆心角为
,
根据弧长公式,可得
,
解得
.
16.
以点
为圆心,以
为半径的圆
17.
【解析】
两圆相交,
圆心距的取值范围是
,
即
.
18.
第三部分
19.
(1)
圆心
??????(2)
半径
??????(3)
圆心角
??????(4)
中心;距离
20.
木板可以平地移动;
理由:木板与地面的距离始终等于莱洛三角形各弧的半径和
的直径.
若
,则
的直径为
,半径为
.
21.
或
.
22.
任取图上不共线三点,两两连线,分别做垂直平分线,交点即为圆心.
23.
(1)
如图所示,
即为所求作;
??????(2)
24.
如图①,当点
与点
重合时,
,,
所以
与
相切,
此时点
运动了
,;
如图②,当点
运动到点
时,过点
作
,垂足为点
,
在
中,,,则
,即
等于
的半径;
所以
与
相切,
此时点
运动了
,;
如图③,当点
运动到
的中点时,
,,
所以
与
相切,
此时点
运动了
,;
如图④,当点
运动到点
的右侧,且
时,过点
作
,交
的延长线于
,
在
中,,则
,即
等于
的半径,
所以直线
与
相切,
此时点
运动了
,.
综上所述,当
时,
的一边所在的直线与
相切.
25.
提示:过点
,
分别作小圆的切线
,,可以证
,则
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
北师大版2020-20201年九年级(下)第三章圆检测试卷A
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1.
已知圆的半径为
,这个圆的内接正六边形的面积为
A.
B.
C.
D.
2.
下列图形中对称轴最多的是
A.
等边三角形
B.
线段
C.
正方形
D.
圆
3.
如图,
中,,,
与
的三边相切于点
,,,若
的半径为
,则
的周长为
A.
B.
C.
D.
4.
如图,点
,,
在同一条直线上,点
在直线外,过这四点中的任意
个点,能画圆的个数是
A.
B.
C.
D.
5.
下列说法错误的是
A.
直径是圆中最长的弦
B.
长度相等的两条弧是等弧
C.
面积相等的两个圆是等圆
D.
半径相等的两个半圆是等弧
6.
已知
的半径为
,圆心
到直线
的距离为
,则正确反映直线
与
的位置关系的图形是
A.
B.
C.
D.
7.
在平面直角坐标系中,
点的坐标为
,以
为半径画
,则以下结论正确的是
A.
与
轴相交,与
轴相切
B.
与
轴相切,与
轴相离
C.
与
轴相离,与
轴相交
D.
与
轴相离,与
轴相切
8.
如果两圆的半径分别是
,,圆心距为
,那么两圆的位置关系是
A.
外切
B.
相交
C.
内切
D.
内含
9.
下列选项中,直线一定是圆的切线的是
A.
与圆有公共点的直线
B.
到圆心的距离等于半径的直线
C.
垂直于圆的半径的直线
D.
过圆的直径的端点的直线
10.
如图,等边三角形
的边长为
,以
上一点
为圆心的圆分别与边
,
相切,则
的半径为
A.
B.
C.
D.
11.
图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形面板翻折起来后,就能形成一个圆形桌面(可近似看做正方形的外接圆),正方形桌面与翻折成的圆形桌面的面积之比最接近于
A.
B.
C.
D.
12.
如图,在同一个圆中作出圆的内接正三角形
和正八边形
,若连接
,则
的度数是
A.
B.
C.
D.
二、填空题(共6小题;每小题4分,共24
分)
13.
如图,直线
,垂足为
,点
在直线
上,,
为直线
上一动点,若以
为半径的
与直线
相切,则
的长为
?.
14.
如图,双曲线
与
在第一象限内交于
,
两点,分别过
,
两点向
轴和
轴作垂线.已知点
的坐标为
,则图中阴影部分的面积为
?.
15.
一个扇形的弧长是
,半径是
,则此扇形的圆心角是
?度.
16.
到点
的距离等于
的点的轨迹是
?.
17.
如果
与
相交,
的半径是
,,那么
的半径
的取值范围是
?.
18.
如图,
是
的割线,
和它的延长线分别交
于
和
,如果
,,,那么
的半径长为
?
.
三、解答题(共7小题;共60分)
19.
(8分)正多边形的有关概念:
(1)中心:是指正多边形的外接圆的
?.
(2)半径:是指正多边形的外接圆的
?.
(3)中心角:是指正多边形每一边所对的
?
角.
(4)边心距:是指正多边形的
?
到它的一边的
?.
20.
(8分)先画正三角形
,然后分别以
,,
为圆心,
的长为半径画弧,得到的图形叫莱洛三角形,如图,将一个莱洛三角形和一个圆放在水平的地面上,上面放一块木板,木板与地面平行,木板是否可以平稳地移动?若
,则
的半径为多少?
21.
(8分)矩形
中,,,如果分别以
,
为圆心的两圆相切,点
在圆
内,点
在圆
外,求圆
的半径
的取值范围.
22.
(8分)如图,有一个圆形工具,请利用直尺和圆规,确定这个圆形工具的圆心.
23.
(8分)如图,等边三角形
的边长为
.
(1)尺规作图作它的外接圆
;
(2)则
的半径为
?.
24.
(10分)如图,
的直径
,在
中,,,,
以
的速度从左向右移动,在运动过程中,
始终在直线
上,设运动的时间为
,当
时,
在
的左侧,,当
为何值时,
的一边所在的直线与
相切?
25.
(10分)如图,在以
为圆心的两个同心圆中,,
为大圆上的任意两点,分别过点
,
作小圆的割线
和
.求证:
答案
第一部分
1.
B
【解析】如图,连接
,,作
,
六边形
是正六边形,
,
,
,
是等边三角形,
,
则
,
2.
D
3.
D
4.
C
【解析】从
,,
三点中任取两点,有
种情况,这
种情况中的每一种情况都与点
构成不在同一直线上的三点,故能画出
个圆.
5.
B
【解析】直径是圆中最长的弦,所以A选项的说法正确;
在同圆或等圆中,长度相等的两条弧是等弧,所以B选项的说法错误;
面积相等的两个圆的半径相等,则它们是等圆,所以C选项的说法正确;
半径相等的两个半圆是等弧,所以D选项的说法正确.
6.
B
【解析】因为圆心
到直线
的距离小于圆的半径且不为
,所以直线
与圆相交且不过圆心.
7.
D
【解析】
点的坐标为
,
点
到
轴的距离为
,到
轴的距离为
,
的半径为
,
圆心
到
轴的距离大于半径,到
轴的距离等于半径,
故
与
轴相离,与
轴相切.
8.
B
9.
B
【解析】与圆只有一个公共点的直线是圆的切线,故A项不符合题意;圆的切线垂直于圆的半径且经过半径的外端,故C项不符合题意;过圆的直径的端点且与该直径垂直的直线是圆的切线,故D项不符合题意.故选B.
10.
A
【解析】设
,
上的切点为
,,由切割线定理可得:
,,,
,
,,,
由勾股定理可得
.
11.
C
【解析】如图,连接
,
设正方形的边长为
,
四边形
是正方形,
,
为圆的直径,
,
则正方形桌面与翻折成的圆形桌面的面积之比为
,故选C.
12.
A
【解析】如图,连接
,,,.
正三角形的中心角
,
正八边形的中心角
,
,
,
.
第二部分
13.
或
14.
15.
【解析】设这个扇形的圆心角为
,
根据弧长公式,可得
,
解得
.
16.
以点
为圆心,以
为半径的圆
17.
【解析】
两圆相交,
圆心距的取值范围是
,
即
.
18.
第三部分
19.
(1)
圆心
??????(2)
半径
??????(3)
圆心角
??????(4)
中心;距离
20.
木板可以平地移动;
理由:木板与地面的距离始终等于莱洛三角形各弧的半径和
的直径.
若
,则
的直径为
,半径为
.
21.
或
.
22.
任取图上不共线三点,两两连线,分别做垂直平分线,交点即为圆心.
23.
(1)
如图所示,
即为所求作;
??????(2)
24.
如图①,当点
与点
重合时,
,,
所以
与
相切,
此时点
运动了
,;
如图②,当点
运动到点
时,过点
作
,垂足为点
,
在
中,,,则
,即
等于
的半径;
所以
与
相切,
此时点
运动了
,;
如图③,当点
运动到
的中点时,
,,
所以
与
相切,
此时点
运动了
,;
如图④,当点
运动到点
的右侧,且
时,过点
作
,交
的延长线于
,
在
中,,则
,即
等于
的半径,
所以直线
与
相切,
此时点
运动了
,.
综上所述,当
时,
的一边所在的直线与
相切.
25.
提示:过点
,
分别作小圆的切线
,,可以证
,则
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
