七年级数学第五讲:三角形综合题
文档属性
| 名称 | 七年级数学第五讲:三角形综合题 |
|
|
| 格式 | zip | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-19 00:00:00 | ||
图片预览


文档简介
第五讲:三角形综合题
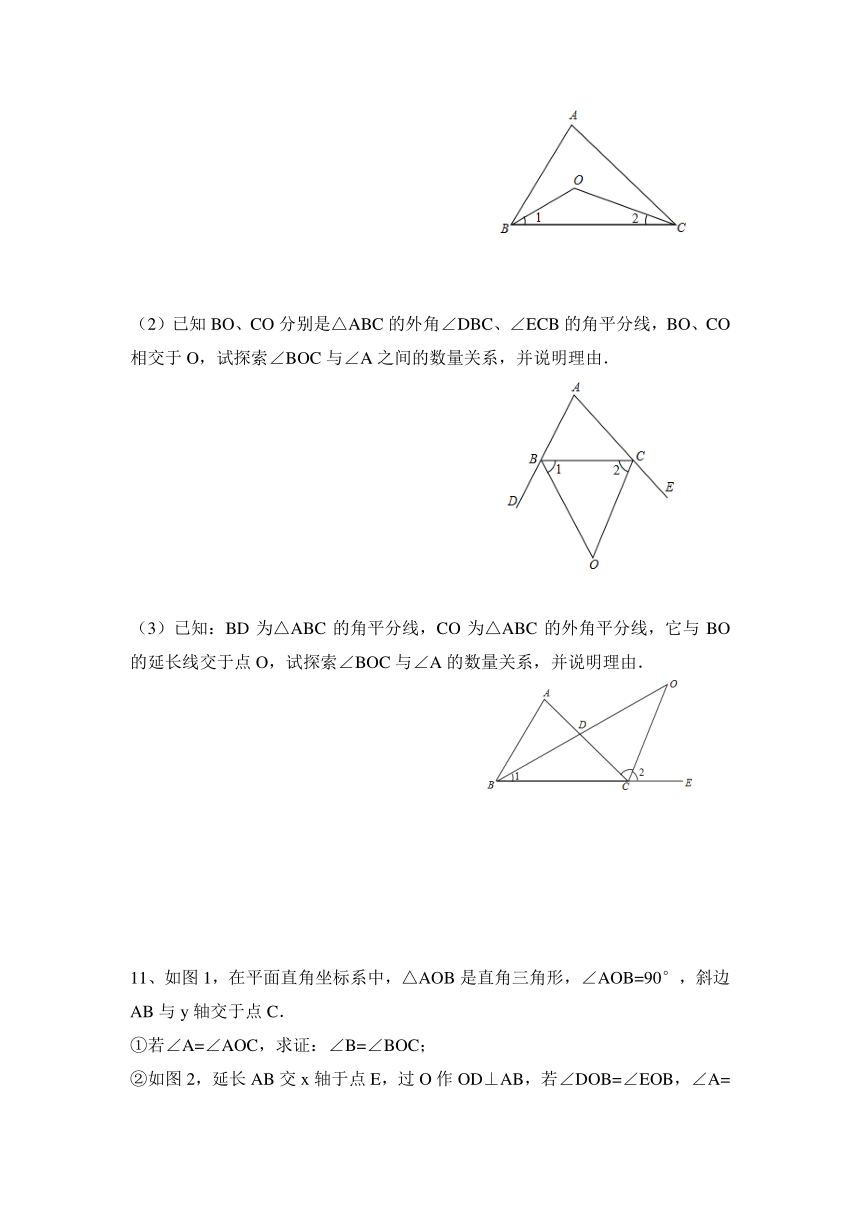
1、如图,在△ABC中,AB=1,BC=2,则△ABC的高AD:CE为 。
2、如图,在△ABC中,点D,E,F分别为BC,AD,AC的中点,且S△ABC=16,则S△DEF的面积为 。
3、如图,△ABC中,点D、E、F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则△ABC的面积是 。
4、如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF= 。
第4题图 第5题图 第6题图
5、如图,△ABC中,AD、BE相交于点O,BD:CD=3:2,AE:CE=2:1。那么S△BOC:S△AOC:S△AOB为( )
A、2:3:4 B、2:3:5 C、3:4:5 D、3:4:6
6、如图,在△ABC中,M是边AB的中点,N是边AC上的点,且AN∶NC=2,CM与BN相交于点K,若△BCK的面积等于1,则△ABC的面积等于( )
A、3 B、 C、4 D、
7、如图,将△ABC的三边AB,BC,CA分别延长至B′,C′,A′,且使BB′=AB,CC′=2BC,AA′=3AC.若S△ABC=1,那么S△A'B'C'是 。
第6题 第7题
8、如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点.PE⊥AD交直线BC于点E.
(1)若∠B=30°,∠ACB=70°,则∠ADC= 度,∠E= 度;
(2)若∠B=58°,∠ACB=102°,则∠ADC= 度,∠E= 度;
(3)若∠B=m°,∠ACB=n°,且n>m,请用含m、n的式子表示∠ADC、∠E的度数.(写出结论即可,不需要证明)
9、(1)如图,BE是∠ABD的平分线.CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,求∠A的大小.
(2)在△ABC中,∠A=50°,高BE、CF交于O,且O不与B、C重合,求∠BOC的度数.
10、(1)已知△ABC中,BO、CO分别是∠ABC、∠ACB的平分线,且BO、CO相交于点O,试探索∠BOC与∠A之间的数量关系,并说明理由.
(2)已知BO、CO分别是△ABC的外角∠DBC、∠ECB的角平分线,BO、CO相交于O,试探索∠BOC与∠A之间的数量关系,并说明理由.
(3)已知:BD为△ABC的角平分线,CO为△ABC的外角平分线,它与BO的延长线交于点O,试探索∠BOC与∠A的数量关系,并说明理由.
11、如图1,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,斜边AB与y轴交于点C.
①若∠A=∠AOC,求证:∠B=∠BOC;
②如图2,延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
③如图3,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(斜边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
12、已知:如图,MN⊥PQ,垂足为O,点A、B分别在射线上OM、OP上,直线BE平分∠PBA与∠BAO的平分线相交于点C.
(1)若∠BAO=45°,求∠ACB;
(2)若点A、B分别在射线上OM、OP上移动,试问∠ACB的大小是否会发生变化?如果保持不变,请说明理由;如果随点A、B的移动发生变化,请求出变化的范围.
13、已知△ABC中,∠BAC=100°.
(1)若∠ABC和∠ACB的角平分线交于点O,如图1,试求∠BOC的大小;
(2)若∠ABC和∠ACB的三等分线(即将一个角平均分成三等分的射线)相交于O,O1,如图2所示,试求∠BOC的大小;
(3)如此类推,若∠ABC和∠ACB的n等分线自下而上依次相交于O,O1,O2…,如图3所示,试探求∠BOC的大小与n的关系,并判断当∠BOC=170°时,是几等分线的交线所成的角.
1、如图,在△ABC中,AB=1,BC=2,则△ABC的高AD:CE为 。
2、如图,在△ABC中,点D,E,F分别为BC,AD,AC的中点,且S△ABC=16,则S△DEF的面积为 。
3、如图,△ABC中,点D、E、F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则△ABC的面积是 。
4、如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF= 。
第4题图 第5题图 第6题图
5、如图,△ABC中,AD、BE相交于点O,BD:CD=3:2,AE:CE=2:1。那么S△BOC:S△AOC:S△AOB为( )
A、2:3:4 B、2:3:5 C、3:4:5 D、3:4:6
6、如图,在△ABC中,M是边AB的中点,N是边AC上的点,且AN∶NC=2,CM与BN相交于点K,若△BCK的面积等于1,则△ABC的面积等于( )
A、3 B、 C、4 D、
7、如图,将△ABC的三边AB,BC,CA分别延长至B′,C′,A′,且使BB′=AB,CC′=2BC,AA′=3AC.若S△ABC=1,那么S△A'B'C'是 。
第6题 第7题
8、如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点.PE⊥AD交直线BC于点E.
(1)若∠B=30°,∠ACB=70°,则∠ADC= 度,∠E= 度;
(2)若∠B=58°,∠ACB=102°,则∠ADC= 度,∠E= 度;
(3)若∠B=m°,∠ACB=n°,且n>m,请用含m、n的式子表示∠ADC、∠E的度数.(写出结论即可,不需要证明)
9、(1)如图,BE是∠ABD的平分线.CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,求∠A的大小.
(2)在△ABC中,∠A=50°,高BE、CF交于O,且O不与B、C重合,求∠BOC的度数.
10、(1)已知△ABC中,BO、CO分别是∠ABC、∠ACB的平分线,且BO、CO相交于点O,试探索∠BOC与∠A之间的数量关系,并说明理由.
(2)已知BO、CO分别是△ABC的外角∠DBC、∠ECB的角平分线,BO、CO相交于O,试探索∠BOC与∠A之间的数量关系,并说明理由.
(3)已知:BD为△ABC的角平分线,CO为△ABC的外角平分线,它与BO的延长线交于点O,试探索∠BOC与∠A的数量关系,并说明理由.
11、如图1,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,斜边AB与y轴交于点C.
①若∠A=∠AOC,求证:∠B=∠BOC;
②如图2,延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
③如图3,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(斜边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
12、已知:如图,MN⊥PQ,垂足为O,点A、B分别在射线上OM、OP上,直线BE平分∠PBA与∠BAO的平分线相交于点C.
(1)若∠BAO=45°,求∠ACB;
(2)若点A、B分别在射线上OM、OP上移动,试问∠ACB的大小是否会发生变化?如果保持不变,请说明理由;如果随点A、B的移动发生变化,请求出变化的范围.
13、已知△ABC中,∠BAC=100°.
(1)若∠ABC和∠ACB的角平分线交于点O,如图1,试求∠BOC的大小;
(2)若∠ABC和∠ACB的三等分线(即将一个角平均分成三等分的射线)相交于O,O1,如图2所示,试求∠BOC的大小;
(3)如此类推,若∠ABC和∠ACB的n等分线自下而上依次相交于O,O1,O2…,如图3所示,试探求∠BOC的大小与n的关系,并判断当∠BOC=170°时,是几等分线的交线所成的角.
