专题16总体取值规律的估计和总体百分位数的估计(同步讲练测)-人教A版(2019)必修 第二册第九章 统计 9.2 用样本估计总体
文档属性
| 名称 | 专题16总体取值规律的估计和总体百分位数的估计(同步讲练测)-人教A版(2019)必修 第二册第九章 统计 9.2 用样本估计总体 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题16总体取值规律的估计和总体百分位数的估计
知识点课前预习与精讲精析
核心知识点1:作频率分布直方图的步骤
(1)求极差:即一组数据中最大值和最小值的差.
(2)决定组距与组数:将数据分组时,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.这时应注意:①一般样本容量越大,所分组数越多;②为方便起见,组距的选择应力求“取整”;③当样本容量不超过100时,按照数据的多少,通常分成5~12组.
(3)将数据分组:按组距将数据分组,分组时,各组均为左闭右开区间,最后一组是闭区间.
(4)列频率分布表.一般分四列:分组、频数累计、频数、频率,最后一行是合计.其中频数合计应是样本容量,频率合计是1.
(5)画频率分布直方图.画图时,应以横轴表示分组,纵轴表示频率/组距.其相应组距上的频率等于该组上的小长方形的面积.
即每个小长方形的面积=组距×=频率.
核心知识点2:频率分布折线图和总体密度曲线
(1)类似于频数分布折线图,连接频率分布直方图中各个小长方形上端的中点,就得到频率分布折线图.
(2)在样本频率分布直方图中,当样本容量逐渐增加,作图时所分的组数增加,组距减小,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.总体密度曲线反映了总体在各个范围内取值的百分比.
核心知识点3:百分位数
(1)如果将一组数据从小到大排序,并计算相应的累计百分位,则某一百分位所对应数据的值就称为这一百分位的百分位数.
一般地,一组数据的第p百分位数是这样一个值,
它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
(2)第25百分位数又称第一四分位数或下四分位数;
第75百分位数又称第三四分位数或上四分位数.
核心知识点4:如何计算百分位数
下面的步骤来说明如何计算第p百分位数.
第1步:以递增顺序排列原始数据(即从小到大排列).
第2步:计算
i=np%.
第3步:①若
i
不是整数,将
i
向上取整.大于i的比邻整数即为第p百分位数的位置;
②若i是整数,则第p百分位数是第i项与第(i+1)项数据的平均值.
1.总体的第p百分位数是一个百分数p∈(0,100),其特点是:总体数据中的任意一个数 它的可能性是p%.
【解析】解:总体的第p百分位数是一个百分数p∈(0,100),
其特点是:总体数据中的任意一个数它的可能性是p%,
故答案为:小于或等于.
2.某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是6人,则参加该英语测试的学生人数是 .
【解析】解:∵成绩低于60分有第在频率分布直方图中,对应矩形的高分别为0.005,0.01,每组数据的组距为20,
则成绩低于60分的频率P=(0.005+0.010)×20=0.3,
∵低于60分的人数是6人,
∴参加该英语测试的学生人数是20.
故答案为:20.
3.为了解M离子在小鼠体内的残留程度,进行如下试验:给100只小鼠服M离子溶液,每只小鼠给服的溶液体积相同、摩尔浓度相同,经过一段时间后检测出残留在小鼠体内离子的百分比.根据试验数据得到如图频率分布直方图,则图中a= ;估计M离子残留百分比的平均数为 .(同组中的每个数据用该组区间的中点值代替)
【解析】解:由题意得:(0.075+0.1+a+0.1+0.05+0.025)×2=1,解得:a=0.1500;
由(0.075×2+0.1×4+0.1501×6+0.1×8+0.05×10+0.025×12)×2=6.1;
故答案为:0.1500,6.1.
4.已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则a= .
【解析】解:由频率分布直方图可知,0.01×10+0.03×10+a×10+0.02×10=1,
所以a=0.04.
故答案为:0.04.
5.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意程度越高,现随机抽取6位小区居号,他们的幸福感指数分别为5,6,7,8,9,5,则这组数据的第80百分位数是( )
A.7
B.7.5
C.8
D.9
【解析】解:该组数据从小到大排列为:
5,5,6,7,8,9.
且6×80%=4.8,
所以这组数据的第80百分位数是8.
故选:C.
典型题型与解题方法
必考必会题型1:频率分布直方图的画法
【典型例题】为了帮助班上的两名贫困生解决经济困难,班上的20名同学捐出了自己的零花钱,他们的捐款数(单位:元)如下:19,20,25,30,24,23,25,29,27,27,28,28,26,27,21,30,20,19,22,20.班主任老师准备将这组数据制成频率分布直方图,以表彰他们的爱心,制图时先计算最大值与最小值的差是 ,若取组距为2,则应分成 组;若第一组的起点定为18.5,则在[26.5,28.5)内的频数为 .
【解析】解:由题意知,极差为30﹣19=11,
由于组距为2,5.5不是整数,所以取6组,
捐款数落在[26.5,28.5)内的有27,27,28,28,27,共5个,因此频数为5.
故答案为:11,6,5.
【题型强化】一组数据的频率分布直方图中,所有小长方形的面积总和为 .
【解析】解:由频率分布直方图得:
一组数据的频率分布直方图中,所有小长方形的面积总和为1.
故答案为:1.
【收官验收】有140位选手参加高尔夫球赛,他们的成绩统计如表:
杆数
65
66
67
68
69
70
71
72
73
74
75
选手数
1
2
5
3
8
17
20
31
22
21
10
(1)列出频率分布表;
(2)画出频数条形图.
【解析】解:(1)由140位选手参加高尔夫球赛的成绩统计表列出频率分布表如下:
区间
频数
频率
[65,68)
8
[68,71)
28
[71,74)
73
[74,77)
31
合计
140
1
(2)画出的频数条形图如下:
必考必会题型2:频率分布直方图的应用
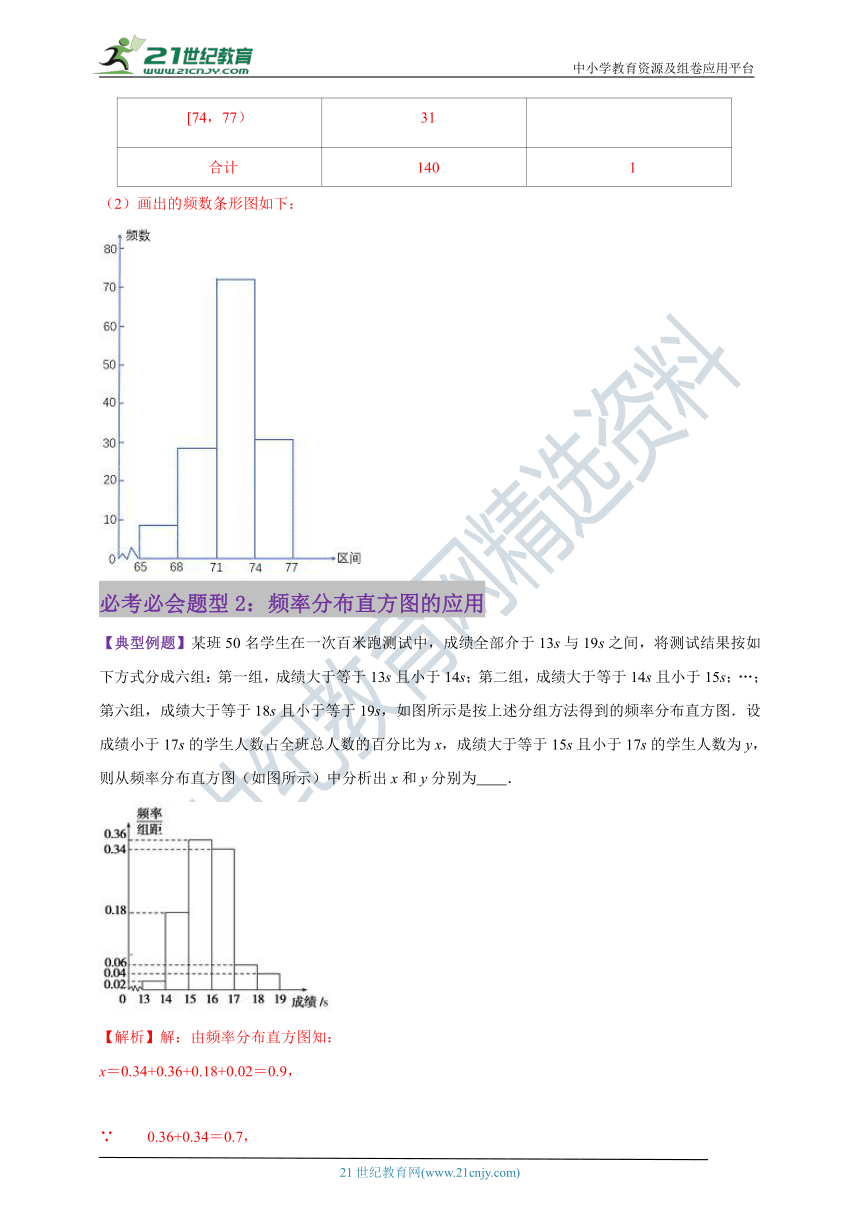
【典型例题】某班50名学生在一次百米跑测试中,成绩全部介于13s与19s之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13s且小于14s;第二组,成绩大于等于14s且小于15s;…;第六组,成绩大于等于18s且小于等于19s,如图所示是按上述分组方法得到的频率分布直方图.设成绩小于17s的学生人数占全班总人数的百分比为x,成绩大于等于15s且小于17s的学生人数为y,则从频率分布直方图(如图所示)中分析出x和y分别为 .
【解析】解:由频率分布直方图知:
x=0.34+0.36+0.18+0.02=0.9,
∵0.36+0.34=0.7,
∴y=35.
故答案为:0.9,35.
【题型强化】对某校高一年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如图柱形图和扇形图.根据图中信息,这些学生成绩的平均数是 .
【解析】解:参加体能测试的人数是12÷30%=40,成绩为3分的人数是40×42.5%=17,
成绩为2分的人数是40﹣3﹣17﹣12=8,
所以这些学生成绩的平均数是2.95.
故答案为:2.95.
【收官验收】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),[60,70),…,[90,100]后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求a,众数,中位数;
(2)估计该校高二年级学生期中考试政治成绩的平均数;
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在[70,90)分数段抽取的人数是多少?
【解析】解(1)由题意可得,(0.01+0.015×2+a+0.025+0.005)×10=1,
解得a=0.03,
根据频率分布直方图可知[70,80)分数段的频率最高,因此众数为75,
又由频率分布直方图可知[40,70)分数段的频率为0.1+0.15+0.15=0.4,因为[70,80)分数段的频率为0.3,
所以,中位数为7010.
(2)估计该校高二年级学生政治成绩的平均数为:
(45×0.01+55×0.015+65×0.015+75×0.03+85×0.025+95×0.005)×10=71.
(3)因为总体共60名学生,样本容量为20,
因此抽样比为.
又在[70,90)分数段共有60×(0.3+0.25)=33(人),
因此,在[70,90)分数段抽取的人数是3311人.
必考必会题型3:百分位数的计算
【典型例题】高二(1)班7人宿舍中每个同学的身高分别为170,168,172,172,175,176,180,求这7人的第40的百分位数为( )
A.168
B.170
C.172
D.171
【解析】解:高二(1)班7人宿舍中每个同学的身高分别为170,168,172,172,175,176,180,
把这7人的身高从小到大排列为:168,170,172,172,175,176,180,
7×40%=2.8,
∴第3个数据为这7人的第40百分位数,即这7人的第40百分位数为172.
故选:C.
【题型强化】某校从高一新生中随机抽取了一个容量为20的身高样本,数据从小到大排序如下(单位:cm):
152,155,158,164,164,165,165,165,166,167,168,168,169,170,170,170,171,x,174,175.若样本数据的第90百分位数是173,则x的值为 .
【解析】解:百分位数的意义就在于,我们可以了解的某一个样本在整个样本集合中所处的位置,本题第90百分位数是173,即比173小的数据占90%,
故答案为:172.
【收官验收】下列数据是30个不同国家中每100000名男性患某种疾病的死亡率:
27.0
23.9
41.6
33.1
40.6
18.8
13.7
28.9
13.2
14.5
27.0
34.8
28.9
3.2
50.1
5.6
8.7
15.2
7.1
5.2
16.5
13.8
19.2
11.2
15.7
10.0
5.6
1.5
33.8
9.2
这组数据的第40百分位数是 .
【解析】解:把这30个数据按照从小到大排列如下,
1.5,3.2,5.2,5.6,5.6,7.1,8.7,9.2,10.0,11.2,
13.2,13.7,13.8,14.5,15.2,15.7,16.5,18.8,19.2,23.9,
27.0,27.0,28.9,28.9,33.1,33.8,34.8,40.6,41.6,50.1;
因为80%×30=24,
所以第80百分位数是第24项与第25项数据的平均数,
即为(28.9+33.1)=31.
故答案为:31.
必考必会题型4:百分位数的综合应用
【典型例题】已知从某中学高一年级随机抽取20名女生,测量她们的身高(单位:cm),把这20名同学的身高数据从小到大排序:
148.0
149.0
150.0
152.0
154.0
154.0
155.0
155.5
157.0
157.0
158.0
159.0
161.0
162.0163.0164.0
165.0
170.0
171.0
172.0
则这组数据的第75百分位数是( )
A.163.0
B.164.0
C.163.5
D.164.5
【解析】解:因为这组数据从小到大已排序,
所以这组数据的第75百分位数为第20×0.75=15个数,即为163.0
故选:A.
【题型强化】样本容量为10的一组样本数据依次为:3,9,0,4,1,6,6,8,2,7,该组数据的第50百分位数是 ,第75百分位数是 .
【解析】解:样本容量为10的一组样本数据依次为:3,9,0,4,1,6,6,8,2,7,
从小到大排列为:0,1,2,3,4,6,6,7,8,9,
∵10×50%=5,
∴该组数据的第50百分位数是,
∵10×75%=7.5,
第75百分位数是7.
故答案为:5,7.
【收官验收】某单位工会有500位会员,利用“健步行APP”开展全员参与的“健步走奖励”活动.假设通过简单随机抽样,获得了50位会员5月10日的走步数据如下:(单位:万步)
1.1
1.4
1.3
1.6
0.3
1.6
0.9
1.4
1.4
0.9
1.4
1.2
1.5
1.6
0.9
1.2
1.2
0.5
0.8
1.0
1.4
0.6
1.0
1.1
0.6
0.8
0.9
0.8
1.1
0.4
0.8
1.4
1.6
1.2
1.0
0.6
1.5
1.6
0.90.7
1.3
1.1
0.8
1.0
1.2
0.6
0.5
0.2
0.8
1.4
频率分布表:
分组
频数
频率
[0.2,0.4)
2
0.04
[0.4,0.6)
a
0.06
[0.6,0.8)
5
0.10
[0.8,1.0)
11
0.22
[1.0,1.2)
8
0.16
[1.2,1.4)
7
0.14
[1.4,1.6]
b
c
合计
50
1.00
(Ⅰ)写出a,b,c的值;
(Ⅱ)(i)绘制频率分布直方图;
(ⅱ)假设同一组中的每个数据可用该组区间的中点值代替,试估计该单位所有会员当日步数的平均值;
(Ⅲ)根据以上50个样本数据,估计这组数据的第70百分位数.你认为如果定1.3万步为健步走获奖标准,一定能保证该单位至少30%的工会会员当日走步获得奖励吗?说明理由.
【解析】解:(Ⅰ)因为0.04+0.06+0.10+0.22+0.16+0.14+c=1,
∴c+0.72=1,
∴c=0.28,
因为共50
人,
∴b=0.28×50=14,
a=0.06×50=3,
∴a=3,b=14,c=0.28.
(Ⅱ)(i)频率分布直方图如下图所示
(ii)设平均值为,则有
=0.012+0.03+0.08+0.198+0.176+0.182+0.42
=1.088,
则该单位所有会员当日步数的平均值为1.088万步.
(Ⅲ)∵70%×50=35,
∴70%分位数为第35和36个数的平均数,
∵[1.4,1.6]共有14人,且1.3有2个,
第35和第36个数均为1.3,
∴70%
分位数为1.3,
设x为会员步数,则x?1.3万时,人数不少于30%,
能保证30%的工会会员获得奖励.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
专题16总体取值规律的估计和总体百分位数的估计
知识点课前预习与精讲精析
核心知识点1:作频率分布直方图的步骤
(1)求极差:即一组数据中最大值和最小值的差.
(2)决定组距与组数:将数据分组时,组数应力求合适,以使数据的分布规律能较清楚地呈现出来.这时应注意:①一般样本容量越大,所分组数越多;②为方便起见,组距的选择应力求“取整”;③当样本容量不超过100时,按照数据的多少,通常分成5~12组.
(3)将数据分组:按组距将数据分组,分组时,各组均为左闭右开区间,最后一组是闭区间.
(4)列频率分布表.一般分四列:分组、频数累计、频数、频率,最后一行是合计.其中频数合计应是样本容量,频率合计是1.
(5)画频率分布直方图.画图时,应以横轴表示分组,纵轴表示频率/组距.其相应组距上的频率等于该组上的小长方形的面积.
即每个小长方形的面积=组距×=频率.
核心知识点2:频率分布折线图和总体密度曲线
(1)类似于频数分布折线图,连接频率分布直方图中各个小长方形上端的中点,就得到频率分布折线图.
(2)在样本频率分布直方图中,当样本容量逐渐增加,作图时所分的组数增加,组距减小,相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.总体密度曲线反映了总体在各个范围内取值的百分比.
核心知识点3:百分位数
(1)如果将一组数据从小到大排序,并计算相应的累计百分位,则某一百分位所对应数据的值就称为这一百分位的百分位数.
一般地,一组数据的第p百分位数是这样一个值,
它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
(2)第25百分位数又称第一四分位数或下四分位数;
第75百分位数又称第三四分位数或上四分位数.
核心知识点4:如何计算百分位数
下面的步骤来说明如何计算第p百分位数.
第1步:以递增顺序排列原始数据(即从小到大排列).
第2步:计算
i=np%.
第3步:①若
i
不是整数,将
i
向上取整.大于i的比邻整数即为第p百分位数的位置;
②若i是整数,则第p百分位数是第i项与第(i+1)项数据的平均值.
1.总体的第p百分位数是一个百分数p∈(0,100),其特点是:总体数据中的任意一个数 它的可能性是p%.
【解析】解:总体的第p百分位数是一个百分数p∈(0,100),
其特点是:总体数据中的任意一个数它的可能性是p%,
故答案为:小于或等于.
2.某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是6人,则参加该英语测试的学生人数是 .
【解析】解:∵成绩低于60分有第在频率分布直方图中,对应矩形的高分别为0.005,0.01,每组数据的组距为20,
则成绩低于60分的频率P=(0.005+0.010)×20=0.3,
∵低于60分的人数是6人,
∴参加该英语测试的学生人数是20.
故答案为:20.
3.为了解M离子在小鼠体内的残留程度,进行如下试验:给100只小鼠服M离子溶液,每只小鼠给服的溶液体积相同、摩尔浓度相同,经过一段时间后检测出残留在小鼠体内离子的百分比.根据试验数据得到如图频率分布直方图,则图中a= ;估计M离子残留百分比的平均数为 .(同组中的每个数据用该组区间的中点值代替)
【解析】解:由题意得:(0.075+0.1+a+0.1+0.05+0.025)×2=1,解得:a=0.1500;
由(0.075×2+0.1×4+0.1501×6+0.1×8+0.05×10+0.025×12)×2=6.1;
故答案为:0.1500,6.1.
4.已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则a= .
【解析】解:由频率分布直方图可知,0.01×10+0.03×10+a×10+0.02×10=1,
所以a=0.04.
故答案为:0.04.
5.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意程度越高,现随机抽取6位小区居号,他们的幸福感指数分别为5,6,7,8,9,5,则这组数据的第80百分位数是( )
A.7
B.7.5
C.8
D.9
【解析】解:该组数据从小到大排列为:
5,5,6,7,8,9.
且6×80%=4.8,
所以这组数据的第80百分位数是8.
故选:C.
典型题型与解题方法
必考必会题型1:频率分布直方图的画法
【典型例题】为了帮助班上的两名贫困生解决经济困难,班上的20名同学捐出了自己的零花钱,他们的捐款数(单位:元)如下:19,20,25,30,24,23,25,29,27,27,28,28,26,27,21,30,20,19,22,20.班主任老师准备将这组数据制成频率分布直方图,以表彰他们的爱心,制图时先计算最大值与最小值的差是 ,若取组距为2,则应分成 组;若第一组的起点定为18.5,则在[26.5,28.5)内的频数为 .
【解析】解:由题意知,极差为30﹣19=11,
由于组距为2,5.5不是整数,所以取6组,
捐款数落在[26.5,28.5)内的有27,27,28,28,27,共5个,因此频数为5.
故答案为:11,6,5.
【题型强化】一组数据的频率分布直方图中,所有小长方形的面积总和为 .
【解析】解:由频率分布直方图得:
一组数据的频率分布直方图中,所有小长方形的面积总和为1.
故答案为:1.
【收官验收】有140位选手参加高尔夫球赛,他们的成绩统计如表:
杆数
65
66
67
68
69
70
71
72
73
74
75
选手数
1
2
5
3
8
17
20
31
22
21
10
(1)列出频率分布表;
(2)画出频数条形图.
【解析】解:(1)由140位选手参加高尔夫球赛的成绩统计表列出频率分布表如下:
区间
频数
频率
[65,68)
8
[68,71)
28
[71,74)
73
[74,77)
31
合计
140
1
(2)画出的频数条形图如下:
必考必会题型2:频率分布直方图的应用
【典型例题】某班50名学生在一次百米跑测试中,成绩全部介于13s与19s之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13s且小于14s;第二组,成绩大于等于14s且小于15s;…;第六组,成绩大于等于18s且小于等于19s,如图所示是按上述分组方法得到的频率分布直方图.设成绩小于17s的学生人数占全班总人数的百分比为x,成绩大于等于15s且小于17s的学生人数为y,则从频率分布直方图(如图所示)中分析出x和y分别为 .
【解析】解:由频率分布直方图知:
x=0.34+0.36+0.18+0.02=0.9,
∵0.36+0.34=0.7,
∴y=35.
故答案为:0.9,35.
【题型强化】对某校高一年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如图柱形图和扇形图.根据图中信息,这些学生成绩的平均数是 .
【解析】解:参加体能测试的人数是12÷30%=40,成绩为3分的人数是40×42.5%=17,
成绩为2分的人数是40﹣3﹣17﹣12=8,
所以这些学生成绩的平均数是2.95.
故答案为:2.95.
【收官验收】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),[60,70),…,[90,100]后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求a,众数,中位数;
(2)估计该校高二年级学生期中考试政治成绩的平均数;
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在[70,90)分数段抽取的人数是多少?
【解析】解(1)由题意可得,(0.01+0.015×2+a+0.025+0.005)×10=1,
解得a=0.03,
根据频率分布直方图可知[70,80)分数段的频率最高,因此众数为75,
又由频率分布直方图可知[40,70)分数段的频率为0.1+0.15+0.15=0.4,因为[70,80)分数段的频率为0.3,
所以,中位数为7010.
(2)估计该校高二年级学生政治成绩的平均数为:
(45×0.01+55×0.015+65×0.015+75×0.03+85×0.025+95×0.005)×10=71.
(3)因为总体共60名学生,样本容量为20,
因此抽样比为.
又在[70,90)分数段共有60×(0.3+0.25)=33(人),
因此,在[70,90)分数段抽取的人数是3311人.
必考必会题型3:百分位数的计算
【典型例题】高二(1)班7人宿舍中每个同学的身高分别为170,168,172,172,175,176,180,求这7人的第40的百分位数为( )
A.168
B.170
C.172
D.171
【解析】解:高二(1)班7人宿舍中每个同学的身高分别为170,168,172,172,175,176,180,
把这7人的身高从小到大排列为:168,170,172,172,175,176,180,
7×40%=2.8,
∴第3个数据为这7人的第40百分位数,即这7人的第40百分位数为172.
故选:C.
【题型强化】某校从高一新生中随机抽取了一个容量为20的身高样本,数据从小到大排序如下(单位:cm):
152,155,158,164,164,165,165,165,166,167,168,168,169,170,170,170,171,x,174,175.若样本数据的第90百分位数是173,则x的值为 .
【解析】解:百分位数的意义就在于,我们可以了解的某一个样本在整个样本集合中所处的位置,本题第90百分位数是173,即比173小的数据占90%,
故答案为:172.
【收官验收】下列数据是30个不同国家中每100000名男性患某种疾病的死亡率:
27.0
23.9
41.6
33.1
40.6
18.8
13.7
28.9
13.2
14.5
27.0
34.8
28.9
3.2
50.1
5.6
8.7
15.2
7.1
5.2
16.5
13.8
19.2
11.2
15.7
10.0
5.6
1.5
33.8
9.2
这组数据的第40百分位数是 .
【解析】解:把这30个数据按照从小到大排列如下,
1.5,3.2,5.2,5.6,5.6,7.1,8.7,9.2,10.0,11.2,
13.2,13.7,13.8,14.5,15.2,15.7,16.5,18.8,19.2,23.9,
27.0,27.0,28.9,28.9,33.1,33.8,34.8,40.6,41.6,50.1;
因为80%×30=24,
所以第80百分位数是第24项与第25项数据的平均数,
即为(28.9+33.1)=31.
故答案为:31.
必考必会题型4:百分位数的综合应用
【典型例题】已知从某中学高一年级随机抽取20名女生,测量她们的身高(单位:cm),把这20名同学的身高数据从小到大排序:
148.0
149.0
150.0
152.0
154.0
154.0
155.0
155.5
157.0
157.0
158.0
159.0
161.0
162.0163.0164.0
165.0
170.0
171.0
172.0
则这组数据的第75百分位数是( )
A.163.0
B.164.0
C.163.5
D.164.5
【解析】解:因为这组数据从小到大已排序,
所以这组数据的第75百分位数为第20×0.75=15个数,即为163.0
故选:A.
【题型强化】样本容量为10的一组样本数据依次为:3,9,0,4,1,6,6,8,2,7,该组数据的第50百分位数是 ,第75百分位数是 .
【解析】解:样本容量为10的一组样本数据依次为:3,9,0,4,1,6,6,8,2,7,
从小到大排列为:0,1,2,3,4,6,6,7,8,9,
∵10×50%=5,
∴该组数据的第50百分位数是,
∵10×75%=7.5,
第75百分位数是7.
故答案为:5,7.
【收官验收】某单位工会有500位会员,利用“健步行APP”开展全员参与的“健步走奖励”活动.假设通过简单随机抽样,获得了50位会员5月10日的走步数据如下:(单位:万步)
1.1
1.4
1.3
1.6
0.3
1.6
0.9
1.4
1.4
0.9
1.4
1.2
1.5
1.6
0.9
1.2
1.2
0.5
0.8
1.0
1.4
0.6
1.0
1.1
0.6
0.8
0.9
0.8
1.1
0.4
0.8
1.4
1.6
1.2
1.0
0.6
1.5
1.6
0.90.7
1.3
1.1
0.8
1.0
1.2
0.6
0.5
0.2
0.8
1.4
频率分布表:
分组
频数
频率
[0.2,0.4)
2
0.04
[0.4,0.6)
a
0.06
[0.6,0.8)
5
0.10
[0.8,1.0)
11
0.22
[1.0,1.2)
8
0.16
[1.2,1.4)
7
0.14
[1.4,1.6]
b
c
合计
50
1.00
(Ⅰ)写出a,b,c的值;
(Ⅱ)(i)绘制频率分布直方图;
(ⅱ)假设同一组中的每个数据可用该组区间的中点值代替,试估计该单位所有会员当日步数的平均值;
(Ⅲ)根据以上50个样本数据,估计这组数据的第70百分位数.你认为如果定1.3万步为健步走获奖标准,一定能保证该单位至少30%的工会会员当日走步获得奖励吗?说明理由.
【解析】解:(Ⅰ)因为0.04+0.06+0.10+0.22+0.16+0.14+c=1,
∴c+0.72=1,
∴c=0.28,
因为共50
人,
∴b=0.28×50=14,
a=0.06×50=3,
∴a=3,b=14,c=0.28.
(Ⅱ)(i)频率分布直方图如下图所示
(ii)设平均值为,则有
=0.012+0.03+0.08+0.198+0.176+0.182+0.42
=1.088,
则该单位所有会员当日步数的平均值为1.088万步.
(Ⅲ)∵70%×50=35,
∴70%分位数为第35和36个数的平均数,
∵[1.4,1.6]共有14人,且1.3有2个,
第35和第36个数均为1.3,
∴70%
分位数为1.3,
设x为会员步数,则x?1.3万时,人数不少于30%,
能保证30%的工会会员获得奖励.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
