专题17总体集中趋势的估计和总体离散程度的估计(同步讲练测) 人教A版(2019)必修 第二册第九章 统计 9.2 用样本估计总体
文档属性
| 名称 | 专题17总体集中趋势的估计和总体离散程度的估计(同步讲练测) 人教A版(2019)必修 第二册第九章 统计 9.2 用样本估计总体 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题17总体集中趋势的估计和总体离散程度的估计
知识点课前预习与精讲精析
核心知识点1:众数
定义
一组数据中出现次数最多的数称为这组数据的众数.
特征
一组数据中的众数可能不止一个,也可能没有,反映了该组数据的集中趋势.
核心知识点2:中位数
定义
一组数据按从小到大的顺序排成一列,处于中间位置的数称为这组数据的中位数.
特征
一组数据中的中位数是唯一的,反映了该组数据的集中趋势.在频率分布直方图中,中位数左边和右边的直方图的面积相等.
核心知识点3:平均数
定义
一组数据的和与这组数的个数的商.数据x1,x2,…,xn的平均数为n=.
特征
平均数对数据有“取齐”的作用,代表该组数据的平均水平.任何一个数据的改变都会引起平均数的变化,这是众数和中位数都不具有的性质.所以与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中极端值的影响较大,使平均数在估计总体时可靠性降低.
核心知识点4:标准差
定义
标准差是样本数据到平均数的一种平均距离,一般用s表示,通常用以下公式来计算s=可以用计算器或计算机计算标准差.
特征
标准差描述一组数据围绕平均数波动的大小,反映了一组数据变化的幅度和离散程度的大小.标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小.
核心知识点5:方差
定义
标准差的平方,即s2=[(x1-)2+(x2-)2+…+(xn-)2]
特征
与标准差的作用相同,描述一组数据围绕平均数波动程度的大小.
1.某班8名学生的体重(单位:kg)分别是:42,48,40,47,43,58,47,45,则这组数据的极差是 ,中位数是 ,25%分位数是 .
【解答】解析 因为所给数据的最大值是58,最小值是40,所以极差是58﹣40=18;
将所给数据按从小到大的顺序排列是40,42,43,45,47,47,48,58,
因为这组数据共8个,处于中间位置的是第4个数和第5个数,
故这组数据的中位数是46;
因为8×25%=2,
所以这组数据的25%分位数是42.5.
故答案为:18;46;42.5.
2.某武警大队共有甲、乙、丙三支中队,人数分别为30,30,40.为了检测该大队的射击水平,从整个大队中用分层随机抽样抽取了30人进行射击考核,统计得三支中队参加射击比赛的平均环数分别为8.8环,8.5环,8.1环,则该武警大队队员的平均射击水平为 环.
【解答】解:该武警大队共有30+30+40=100人,则甲中队参加考核的人数为人,乙中队参加考核的人数为人,丙中队参加考核的人数为人,
所以参加考核的30人的平均射击环数为8.43环,即该武警大队队员的平均射击水平为8.43环.
故答案为:8.43.
3.为了考察某超市一年中每天的营业额,从中抽取了30天的日营业额.在这个问题中,总体是 ,样本是 .
【解答】解:由总体、样本的概念结合题意可知:
在这个问题中,总体是该超市一年中每天的营业额,
样本是抽取的30天的日营业额.
故答案为:该超市一年中每天的营业额;抽取的30天的日营业额.
4.为了鉴定某种节能灯泡的质量,对其中100只节能灯泡的使用寿命进行测量,结果如表:(单位:小时)
寿命
450
550
600
650
700
只数
20
10
30
15
25
则这些节能灯泡使用寿命的平均数是 .
【解答】解:这些节能灯泡使用寿命的平均数是:
597.5.
故答案为:597.5.
5.从某个渔场通过简单随机抽样方法检查了30条鱼的质量(单位:g)如下:
254
298
320
325
347
354
362
367
369
372
379
380
382
386
391
397
397
411
412
419
422
435
438
443
447
452
480
506
524
539
(1)制作频率分布表;
(2)制作频率直方图;
(3)制作频率折线图;
(4)制作茎叶图;
(5)计算样本均值;
(6)计算样本方差.
【解答】解:(1)这组数据的最大值为539,最小值为254,极差为285,可将其分为8组,组距为430.频率分布表如下:
鱼的质量
发生次数
发生频率
(250,300]
2
0.067
(300,350]
3
0.10
(350,400]
12
0.40
(400,450]
8
0.266
(450,500]
2
0.067
(500,550]
3
0.1
合计
30
1
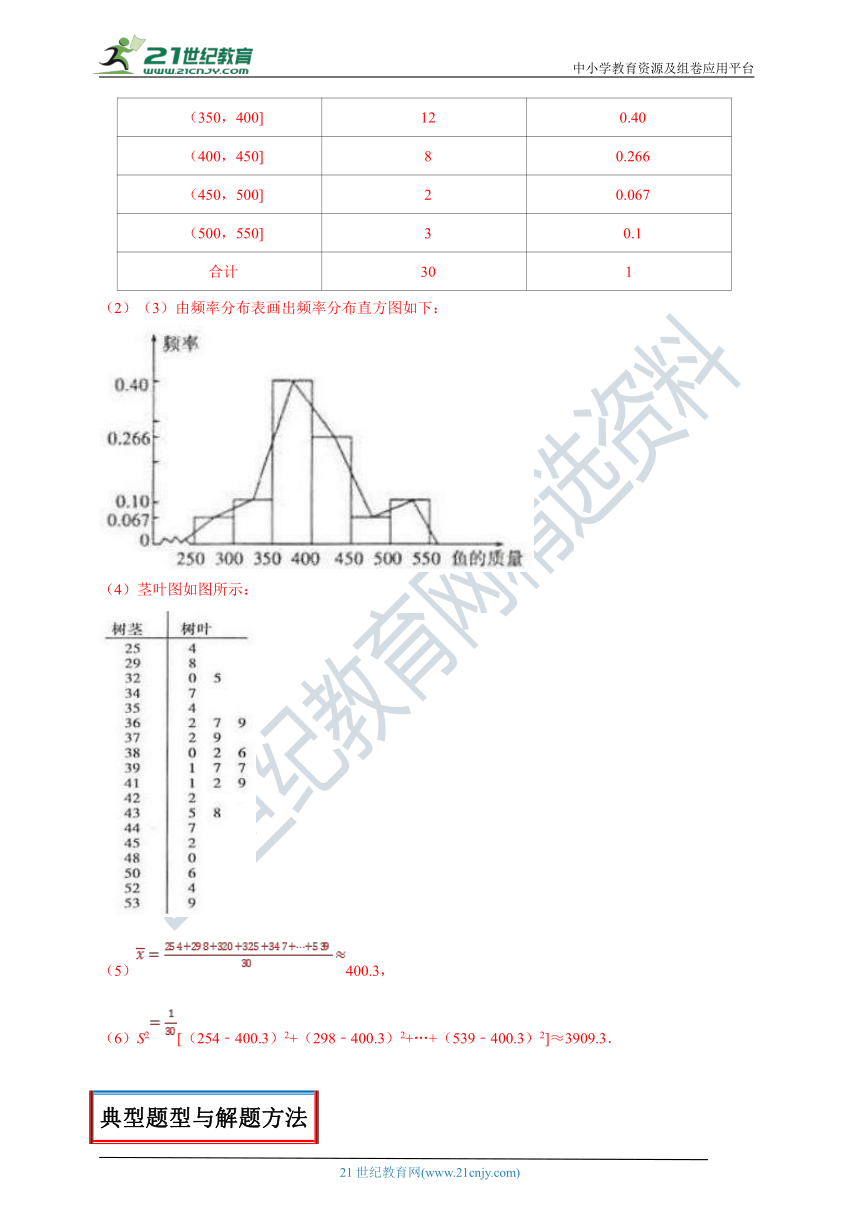
(2)(3)由频率分布表画出频率分布直方图如下:
(4)茎叶图如图所示:
(5)400.3,
(6)S2[(254﹣400.3)2+(298﹣400.3)2+…+(539﹣400.3)2]≈3909.3.
典型题型与解题方法
必考必会题型1:平均数、中位数和众数的计算
【典型例题】任何疫苗在上市前都要经过反复试验和检测,以确保其安全有效,某种预防新冠肺炎的疫苗在5个国家进行临床试验,统计得到的疫苗有效率分别为95%,94%,69%,91%,86%,则这组数据的平均数为 .
【解析】解:根据题意可得,这组数据的平均数为100%=87%.
故答案为:87%.
【题型强化】在某次数学测验中,6位学生的成绩如下:78,85,a,82,69,80,他们得平均成绩为80,他们成绩的中位数为 .
【解析】解:因为6位学生的成绩如下:78,85,a,82,69,80,他们得平均成绩为80,
所以78+85+a+82+69+80=6×80,解得a=86,
则将6位学生的成绩从小到大排列为:69,78,80,82,85,86,
所以他们成绩的中位数为.
故答案为:81.
【收官验收】若一组数据x1,x2,x3,…,xn的平均数是30,另一组数据x1+y1,x2+y2,x3+y3,…,xn+yn的平均数是70,则第三组数据4y1+1,4y2+1,4y3+1,…,4yn+1的平均数是 .
【解析】解:数据x1+y1,x2+y2,x3+y3,…,xn+yn共有n个,
其平均数为.因此
故数据4y1+1,4y2+1,4y3+1,…,4yn+1的平均数是4×40+1=161.
故答案为:161.
必考必会题型2:平均数、中位数、众数的应用
【典型例题】求下列一组数据的最值、极差、平均数、中位数与众数.
8,10,9,13,15,9,10,11,9,16
【解析】解:这组数据从小到大排序为:
8,9,9,9,10,10,11,13,15,16,
最大值为16,最小值为8,
极差为:16﹣8=8,
平均数为:11,
中位数为:10
众数为:9.
【题型强化】银川市展览馆22天中每天进馆参观的人数如下:
180
158
170
185
189
180
184
185
140
179
192
185
190
165
182
170
190
183
175
180
185
148
计算参观人数的中位数、众数、平均数、标准差(保留整数部分).
【解析】解:将数据按从小到大的顺序排列,140,148,158,165,170,170,175,179,180,180,180,182,183,184,185,185,185,185,189,190,190,192,
第十一个数180,第十二个数182,中位数为181;
因为185有4个,其余数都少于4个,所以众数185;
平均数(180+158+…+148)÷22≈177;
标准差s13.35.
【收官验收】高一(3)班有男同学27名,女同学21名.在一次语文测验中,男同学得分的平均数是82,中位数是75,女同学得分的平均数是80,中位数是80.
(1)求这次测验全班成绩的平均数(精确到0.01);
(2)估计全班成绩不超过80分的同学至少有多少人;
(3)分析男同学得分的平均数与中位数相差较大的主要原因.
【解析】解:(1)利用平均数计算公式,得这次测验全班成绩的平均数为:
(82×27+80×21)≈81.13.
(2)因为男同学得分的中位数是75,
所以至少有14名男生得分不超过75分.
又因为女同学得分的中位数是80,
所以至少有11名女生得分不超过80分.
所以全班至少有25人得分不超过80分.
(3)男同学得分的平均数与中位数相差较大,
说明男同学中两极分化现象严重,得分高的和得分低的相差较大.
必考必会题型3:根据频率分布直方图求平均数中位数和众数
【典型例题】如图是一次考试结果的频数分布直方图,请据此估计这次考试的平均分.
【解析】解:由频数分布直方图估计这次考试的平均分为:
46.
∴估计这次考试的平均分为46分.
【题型强化】某校2017﹣2018学年高二某个班的一次化学考试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图:
(1)求分数在[50,60)的频率及在全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(3)利用频率分布直方图估计这个班此次化学成绩的中位数.
【解析】解:(1)由频率分布直方图知分数在[50,60)的频率为:
0.008×10=0.08.
由茎叶图知分数在[50,60)间的人数为2人,
∴全班人数为:25人.
(2)由(1)和茎叶图,知:
分数在[80,90)之间的频数为:25﹣2﹣7﹣11﹣2=3,
频率分布直方图中间矩形[80,90)的高为:10=0.012.
(3)由题意化学成绩的中位数从小到大排列是第13个,
结合茎叶图得中位数是74.
【收官验收】某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,画出如图所示部分频率分布直方图.观察图形,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试成绩的中位数(结果取整数值);
(3)估计这次考试的平均分.
【解析】解:(1)因为各组的频率和等于1,
故第四组的频率:
f4=1﹣(0.025+0.015×2+0.01+0.005)×10=0.3,
直方图如右所示.
(2)成绩在[40,70)的频率为:
(0.01+0.015+0.015)×10=0.4,
成绩在[40,80)的频率为:
0.4+0.03×10=0.7,
∴中位数在[70,80)内,
设中位数为x,
∵中位数要平分直方图的面积,
∴x=7073.
(3)依题意,60及以上的分数所在的第频率和为(0.015+0.03+0.025+0.005)×10=0.75
所以,抽样学生成绩的合格率是75%,
利用组中值估算抽样学生的平均分为:
45?f1+55?f2+65?f3+75?f4+85?f5+95?f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
估计这次考试的平均分是71(分).
必考必会题型4:方差和标准差的计算
【典型例题】2019年全国奥数冬令营甲、乙两组分别为30人、24人,第二轮测试中,甲组平均成绩为40分,方差为300,乙组平均成绩为42分,方差为260,那么甲乙两组全部54人的方差为 (保留两位小数).
【解析】解:由W甲,W乙,40,42,
故4042=40.89,
300,260,
故全部54人的方差S2?[300+(40﹣40.89)2]?[260+(42﹣40.89)2]≈283.21,
故答案为:283.21.
【题型强化】在某年的足球联赛中,甲球队每场比赛平均失球数是1.8,全年比赛失球个数的标准差为1.1;乙球队每场比赛平均失球数是1.5,全年失球个数的标准差是0.6,有下列说法:
①平均说来甲球队的成绩比乙球队的成绩好;
②乙球队比甲球队防守状况更稳定.
其中,正确的有 .
【解析】解:①,因为甲球队每场比赛平均失球数是1.8,乙球队每场比赛平均失球数是1.5,
所以甲球队每场比赛平均失球数大于乙球队每场比赛平均失球数,
所以平均说来乙球队的成绩比甲球队的成绩好;故①错误,
②,甲球队全年比赛失球个数的标准差为1.1,乙球队全年失球个数的标准差是0.6,
所以甲球队全年比赛失球个数的标准差为大于乙球队全年失球个数的标准差是0.6,
所以乙球队比甲球队防守状况更稳定.故②正确.
故选:②.
【收官验收】已知一组数x1,x2,…,xn的方差是4,则2x1﹣1,2x2﹣1,…,2xn﹣1的标准差是 .
【解析】解:设x1,x2,…,xn的平均数是(x1+x2+…+xn),
方差是s2[]=4;
∴2x1﹣1,2x2﹣1,…,2xn﹣1的平均数是
[(2x1﹣1)+(2x2﹣1)+..+(2xn﹣1)][2(x1+x2+…+xn)﹣n]=21,
∴方差是s′2[]
[]=4s2=4×4=16;
∴标准差是s′=4.
故答案为:4.
必考必会题型5:分层随机抽样的方差
【典型例题】已知一组样本数据x1,x2,…,x10,且x12+x22+…+x102=2020,平均数11,则该组数据的标准差为 .
【解析】解:一组样本数据x1,x2,…,x10,且x12+x22+…+x102=2020,平均数11,
则该组数据的方差为[(x1﹣11)2+(x2﹣11)2+…+(x10﹣11)2]
[(x12+x22+…+x102)+10×121﹣22(x1+x2+…+x10)]
(2020+1210﹣22×110)
=81,
∴该组数据的标准差为9.
故答案为:9.
【题型强化】已知某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的平均数为,方差为s2,则?s2= .
【解析】解:∵某7个数的平均数为4,方差为2,现加入一个新数据4,
∴此时这8个数的平均数为(4×7+4)=4,
方差为s2(7×2+02),则?s2=47.
故答案为:7.
【收官验收】已知样本x1,x2,x3,…,xn方差s2=1,则样本2x1+1,2x2+1,2x3+1,…,2xn+1的方差为 .
【解析】解:∵样本x1,x2,x3,…,xn方差s2=1,
∴样本2x1+1,2x2+1,2x3+1,…,2xn+1的方差为:
4s2=4.
故答案为:4.
必考必会题型6:数据的数字特征的综合应用
【典型例题】据报道,某销售公司有33名职工,他们所在部门及相应每人所创年利润如表所示(单位:万元):
部门
A
B
C
D
E
F
G
人数
1
1
2
1
5
3
20
每人所创年利润
5.5
5
3.5
3
2.5
2
1.5
(1)求该公司职工每人所创年利润的平均数、中位数、众数、极差;
(2)假设部门A所创年利润从5.5万元提高到30万元,部门B所创年利润由5万元提高到20万元,那么新的平均数、中位数、众数、极差又是多少?
(3)你认为哪个统计量更能反映这个公司职工每人所创年利润的平均水平?
【解析】解:(1)2.1,中位数为1.5,众数为1.5,极差为4.
(2)3.3,中位数为1.5,众数为1.5,极差为28.5.
(3)中位数或众数均能反映该公司职工每人所创年利润的平均水平,
这是因为公司中少数人每人所创年利润与大多数人每人所创年利润差别较大,这样导致平均数与中位数或众数偏差较大,
所以平均数不能反映这个公司职工每人所创年利润的平均水平.
【题型强化】某大型超市抽查了100天该超市的日纯利润数据,并分成了以下几组(单位:万元):[4,5),[5,6),[6,7),[7,8),[8,9),[9,10].统计结果如表所示(统计表中每个小组取中间值作为该组数据的替代值):
组别
[4,5)
[5,6)
[6,7)
[7,8)
[8,9)
[9,10]
频数
5
20
30
30
10
5
(1)求这100天该大型超市日纯利润的平均数及中位数;
(2)利用上述样本分布估计总体分布,解决下面问题:该大型超市总经理根据每天的纯利润给员工制定了两种奖励方案:
方案一:记日纯利润为x万元,当x<6时,奖励每位员工40元/天;当6≤x<8时,奖励每位员工80元/天;当x≥8时,奖励每位员工120元/天;
方案二:日纯利润低于总体中位数时每名员工发放奖金50元/天,日纯利润不低于总体中位数时每名员工发放80元奖金/天;
“小张恰好为该大型超市的一位员工,则从统计角度看,小张选择哪种奖励方案更有利?
【解析】解:(1)这100天该大型超市日纯利涧的平均数为:(4.5×5+5.5×20+6.5×30+7.5×30+8.5×10+9.5×5)=6.85(万元),
前2组频率之和为:0.05+0.20=0.25<0.5,前3组频率之和为:0.25+0.3=0.55>0.5,故中位数位于第3组;
设中位数为t则有(t﹣6)×0.3+0.25=0.5
解得:t;
即这100天该大型超市日纯利润的中位数为万元;
(2)设选择方案一时,小张每天的奖金为x元,
则x的可能取值为40,80,120,其对应的概率分别为0.25,0.6,0.15,
所以获得奖金的平均数40×0.25+80×0.6+120×0.15=76(元)
设选择方案二时小张每天的奖金为y元
则获得奖金的平均数50×0.5+80×0.5=65(元)
因为x>y,
所以从统计角度看,小张选择方案一更有利.
【收官验收】某制造商生产长度为6cm的金属棒,抽样检查40根,测得每根长度(单位:cm,保留两位小数)如下:
6.02
6.01
5.94
5.94
5.97
5.96
5.98
6.01
5.98
5.99
6.00
6.03
5.99
5.97
5.98
6.00
6.03
5.95
6.00
6.00
5.92
5.93
5.99
5.99
6.00
5.95
6.00
5.97
5.96
5.97
6.03
6.01
5.98
5.99
6.04
6.00
6.02
5.97
5.96
5.98
(1)计算上述样本中金属棒的平均长度;
(2)画出频率分布直方图;
(3)如果允许制造商生产这种金属棒与6cm的标准有0.2%的离差,那么抽样检查中合格的金属棒有几根?合格率是多少?
【解析】解:(1)(6.02+6.01+5.94+5.94+5.97+5.96+5.98+6.01+5.98+5.99+6.00+6.03+5.99+5.97+5.98+6.00+6.03+5.95+6.00+6.00+5.92+5.93+5.99+5.99+6.00+5.95+6.00+5.97+5.96+5.97+6.03+6.01+5.98+5.99+6.04+6.00+6.02+5.97+5.96+5.98)÷40=5.99cm;
(2)频率分布表如下:
分组
频数
频率
[5.92,5.95)
4
0.1
[5.95,5.98)
10
0.25
[5.98,6.01)
17
0.425
[6.01,6.04)
9
0.225
合计
40
1
频率分布直方图如下:
(3)6×(1﹣0.2%)=5.99,6×(1+0.2%)=6.01,
故合格的金属棒有15根,合格率约为15÷40=37.5%.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
专题17总体集中趋势的估计和总体离散程度的估计
知识点课前预习与精讲精析
核心知识点1:众数
定义
一组数据中出现次数最多的数称为这组数据的众数.
特征
一组数据中的众数可能不止一个,也可能没有,反映了该组数据的集中趋势.
核心知识点2:中位数
定义
一组数据按从小到大的顺序排成一列,处于中间位置的数称为这组数据的中位数.
特征
一组数据中的中位数是唯一的,反映了该组数据的集中趋势.在频率分布直方图中,中位数左边和右边的直方图的面积相等.
核心知识点3:平均数
定义
一组数据的和与这组数的个数的商.数据x1,x2,…,xn的平均数为n=.
特征
平均数对数据有“取齐”的作用,代表该组数据的平均水平.任何一个数据的改变都会引起平均数的变化,这是众数和中位数都不具有的性质.所以与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中极端值的影响较大,使平均数在估计总体时可靠性降低.
核心知识点4:标准差
定义
标准差是样本数据到平均数的一种平均距离,一般用s表示,通常用以下公式来计算s=可以用计算器或计算机计算标准差.
特征
标准差描述一组数据围绕平均数波动的大小,反映了一组数据变化的幅度和离散程度的大小.标准差较大,数据的离散程度较大;标准差较小,数据的离散程度较小.
核心知识点5:方差
定义
标准差的平方,即s2=[(x1-)2+(x2-)2+…+(xn-)2]
特征
与标准差的作用相同,描述一组数据围绕平均数波动程度的大小.
1.某班8名学生的体重(单位:kg)分别是:42,48,40,47,43,58,47,45,则这组数据的极差是 ,中位数是 ,25%分位数是 .
【解答】解析 因为所给数据的最大值是58,最小值是40,所以极差是58﹣40=18;
将所给数据按从小到大的顺序排列是40,42,43,45,47,47,48,58,
因为这组数据共8个,处于中间位置的是第4个数和第5个数,
故这组数据的中位数是46;
因为8×25%=2,
所以这组数据的25%分位数是42.5.
故答案为:18;46;42.5.
2.某武警大队共有甲、乙、丙三支中队,人数分别为30,30,40.为了检测该大队的射击水平,从整个大队中用分层随机抽样抽取了30人进行射击考核,统计得三支中队参加射击比赛的平均环数分别为8.8环,8.5环,8.1环,则该武警大队队员的平均射击水平为 环.
【解答】解:该武警大队共有30+30+40=100人,则甲中队参加考核的人数为人,乙中队参加考核的人数为人,丙中队参加考核的人数为人,
所以参加考核的30人的平均射击环数为8.43环,即该武警大队队员的平均射击水平为8.43环.
故答案为:8.43.
3.为了考察某超市一年中每天的营业额,从中抽取了30天的日营业额.在这个问题中,总体是 ,样本是 .
【解答】解:由总体、样本的概念结合题意可知:
在这个问题中,总体是该超市一年中每天的营业额,
样本是抽取的30天的日营业额.
故答案为:该超市一年中每天的营业额;抽取的30天的日营业额.
4.为了鉴定某种节能灯泡的质量,对其中100只节能灯泡的使用寿命进行测量,结果如表:(单位:小时)
寿命
450
550
600
650
700
只数
20
10
30
15
25
则这些节能灯泡使用寿命的平均数是 .
【解答】解:这些节能灯泡使用寿命的平均数是:
597.5.
故答案为:597.5.
5.从某个渔场通过简单随机抽样方法检查了30条鱼的质量(单位:g)如下:
254
298
320
325
347
354
362
367
369
372
379
380
382
386
391
397
397
411
412
419
422
435
438
443
447
452
480
506
524
539
(1)制作频率分布表;
(2)制作频率直方图;
(3)制作频率折线图;
(4)制作茎叶图;
(5)计算样本均值;
(6)计算样本方差.
【解答】解:(1)这组数据的最大值为539,最小值为254,极差为285,可将其分为8组,组距为430.频率分布表如下:
鱼的质量
发生次数
发生频率
(250,300]
2
0.067
(300,350]
3
0.10
(350,400]
12
0.40
(400,450]
8
0.266
(450,500]
2
0.067
(500,550]
3
0.1
合计
30
1
(2)(3)由频率分布表画出频率分布直方图如下:
(4)茎叶图如图所示:
(5)400.3,
(6)S2[(254﹣400.3)2+(298﹣400.3)2+…+(539﹣400.3)2]≈3909.3.
典型题型与解题方法
必考必会题型1:平均数、中位数和众数的计算
【典型例题】任何疫苗在上市前都要经过反复试验和检测,以确保其安全有效,某种预防新冠肺炎的疫苗在5个国家进行临床试验,统计得到的疫苗有效率分别为95%,94%,69%,91%,86%,则这组数据的平均数为 .
【解析】解:根据题意可得,这组数据的平均数为100%=87%.
故答案为:87%.
【题型强化】在某次数学测验中,6位学生的成绩如下:78,85,a,82,69,80,他们得平均成绩为80,他们成绩的中位数为 .
【解析】解:因为6位学生的成绩如下:78,85,a,82,69,80,他们得平均成绩为80,
所以78+85+a+82+69+80=6×80,解得a=86,
则将6位学生的成绩从小到大排列为:69,78,80,82,85,86,
所以他们成绩的中位数为.
故答案为:81.
【收官验收】若一组数据x1,x2,x3,…,xn的平均数是30,另一组数据x1+y1,x2+y2,x3+y3,…,xn+yn的平均数是70,则第三组数据4y1+1,4y2+1,4y3+1,…,4yn+1的平均数是 .
【解析】解:数据x1+y1,x2+y2,x3+y3,…,xn+yn共有n个,
其平均数为.因此
故数据4y1+1,4y2+1,4y3+1,…,4yn+1的平均数是4×40+1=161.
故答案为:161.
必考必会题型2:平均数、中位数、众数的应用
【典型例题】求下列一组数据的最值、极差、平均数、中位数与众数.
8,10,9,13,15,9,10,11,9,16
【解析】解:这组数据从小到大排序为:
8,9,9,9,10,10,11,13,15,16,
最大值为16,最小值为8,
极差为:16﹣8=8,
平均数为:11,
中位数为:10
众数为:9.
【题型强化】银川市展览馆22天中每天进馆参观的人数如下:
180
158
170
185
189
180
184
185
140
179
192
185
190
165
182
170
190
183
175
180
185
148
计算参观人数的中位数、众数、平均数、标准差(保留整数部分).
【解析】解:将数据按从小到大的顺序排列,140,148,158,165,170,170,175,179,180,180,180,182,183,184,185,185,185,185,189,190,190,192,
第十一个数180,第十二个数182,中位数为181;
因为185有4个,其余数都少于4个,所以众数185;
平均数(180+158+…+148)÷22≈177;
标准差s13.35.
【收官验收】高一(3)班有男同学27名,女同学21名.在一次语文测验中,男同学得分的平均数是82,中位数是75,女同学得分的平均数是80,中位数是80.
(1)求这次测验全班成绩的平均数(精确到0.01);
(2)估计全班成绩不超过80分的同学至少有多少人;
(3)分析男同学得分的平均数与中位数相差较大的主要原因.
【解析】解:(1)利用平均数计算公式,得这次测验全班成绩的平均数为:
(82×27+80×21)≈81.13.
(2)因为男同学得分的中位数是75,
所以至少有14名男生得分不超过75分.
又因为女同学得分的中位数是80,
所以至少有11名女生得分不超过80分.
所以全班至少有25人得分不超过80分.
(3)男同学得分的平均数与中位数相差较大,
说明男同学中两极分化现象严重,得分高的和得分低的相差较大.
必考必会题型3:根据频率分布直方图求平均数中位数和众数
【典型例题】如图是一次考试结果的频数分布直方图,请据此估计这次考试的平均分.
【解析】解:由频数分布直方图估计这次考试的平均分为:
46.
∴估计这次考试的平均分为46分.
【题型强化】某校2017﹣2018学年高二某个班的一次化学考试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图:
(1)求分数在[50,60)的频率及在全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(3)利用频率分布直方图估计这个班此次化学成绩的中位数.
【解析】解:(1)由频率分布直方图知分数在[50,60)的频率为:
0.008×10=0.08.
由茎叶图知分数在[50,60)间的人数为2人,
∴全班人数为:25人.
(2)由(1)和茎叶图,知:
分数在[80,90)之间的频数为:25﹣2﹣7﹣11﹣2=3,
频率分布直方图中间矩形[80,90)的高为:10=0.012.
(3)由题意化学成绩的中位数从小到大排列是第13个,
结合茎叶图得中位数是74.
【收官验收】某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,画出如图所示部分频率分布直方图.观察图形,回答下列问题:
(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试成绩的中位数(结果取整数值);
(3)估计这次考试的平均分.
【解析】解:(1)因为各组的频率和等于1,
故第四组的频率:
f4=1﹣(0.025+0.015×2+0.01+0.005)×10=0.3,
直方图如右所示.
(2)成绩在[40,70)的频率为:
(0.01+0.015+0.015)×10=0.4,
成绩在[40,80)的频率为:
0.4+0.03×10=0.7,
∴中位数在[70,80)内,
设中位数为x,
∵中位数要平分直方图的面积,
∴x=7073.
(3)依题意,60及以上的分数所在的第频率和为(0.015+0.03+0.025+0.005)×10=0.75
所以,抽样学生成绩的合格率是75%,
利用组中值估算抽样学生的平均分为:
45?f1+55?f2+65?f3+75?f4+85?f5+95?f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
估计这次考试的平均分是71(分).
必考必会题型4:方差和标准差的计算
【典型例题】2019年全国奥数冬令营甲、乙两组分别为30人、24人,第二轮测试中,甲组平均成绩为40分,方差为300,乙组平均成绩为42分,方差为260,那么甲乙两组全部54人的方差为 (保留两位小数).
【解析】解:由W甲,W乙,40,42,
故4042=40.89,
300,260,
故全部54人的方差S2?[300+(40﹣40.89)2]?[260+(42﹣40.89)2]≈283.21,
故答案为:283.21.
【题型强化】在某年的足球联赛中,甲球队每场比赛平均失球数是1.8,全年比赛失球个数的标准差为1.1;乙球队每场比赛平均失球数是1.5,全年失球个数的标准差是0.6,有下列说法:
①平均说来甲球队的成绩比乙球队的成绩好;
②乙球队比甲球队防守状况更稳定.
其中,正确的有 .
【解析】解:①,因为甲球队每场比赛平均失球数是1.8,乙球队每场比赛平均失球数是1.5,
所以甲球队每场比赛平均失球数大于乙球队每场比赛平均失球数,
所以平均说来乙球队的成绩比甲球队的成绩好;故①错误,
②,甲球队全年比赛失球个数的标准差为1.1,乙球队全年失球个数的标准差是0.6,
所以甲球队全年比赛失球个数的标准差为大于乙球队全年失球个数的标准差是0.6,
所以乙球队比甲球队防守状况更稳定.故②正确.
故选:②.
【收官验收】已知一组数x1,x2,…,xn的方差是4,则2x1﹣1,2x2﹣1,…,2xn﹣1的标准差是 .
【解析】解:设x1,x2,…,xn的平均数是(x1+x2+…+xn),
方差是s2[]=4;
∴2x1﹣1,2x2﹣1,…,2xn﹣1的平均数是
[(2x1﹣1)+(2x2﹣1)+..+(2xn﹣1)][2(x1+x2+…+xn)﹣n]=21,
∴方差是s′2[]
[]=4s2=4×4=16;
∴标准差是s′=4.
故答案为:4.
必考必会题型5:分层随机抽样的方差
【典型例题】已知一组样本数据x1,x2,…,x10,且x12+x22+…+x102=2020,平均数11,则该组数据的标准差为 .
【解析】解:一组样本数据x1,x2,…,x10,且x12+x22+…+x102=2020,平均数11,
则该组数据的方差为[(x1﹣11)2+(x2﹣11)2+…+(x10﹣11)2]
[(x12+x22+…+x102)+10×121﹣22(x1+x2+…+x10)]
(2020+1210﹣22×110)
=81,
∴该组数据的标准差为9.
故答案为:9.
【题型强化】已知某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的平均数为,方差为s2,则?s2= .
【解析】解:∵某7个数的平均数为4,方差为2,现加入一个新数据4,
∴此时这8个数的平均数为(4×7+4)=4,
方差为s2(7×2+02),则?s2=47.
故答案为:7.
【收官验收】已知样本x1,x2,x3,…,xn方差s2=1,则样本2x1+1,2x2+1,2x3+1,…,2xn+1的方差为 .
【解析】解:∵样本x1,x2,x3,…,xn方差s2=1,
∴样本2x1+1,2x2+1,2x3+1,…,2xn+1的方差为:
4s2=4.
故答案为:4.
必考必会题型6:数据的数字特征的综合应用
【典型例题】据报道,某销售公司有33名职工,他们所在部门及相应每人所创年利润如表所示(单位:万元):
部门
A
B
C
D
E
F
G
人数
1
1
2
1
5
3
20
每人所创年利润
5.5
5
3.5
3
2.5
2
1.5
(1)求该公司职工每人所创年利润的平均数、中位数、众数、极差;
(2)假设部门A所创年利润从5.5万元提高到30万元,部门B所创年利润由5万元提高到20万元,那么新的平均数、中位数、众数、极差又是多少?
(3)你认为哪个统计量更能反映这个公司职工每人所创年利润的平均水平?
【解析】解:(1)2.1,中位数为1.5,众数为1.5,极差为4.
(2)3.3,中位数为1.5,众数为1.5,极差为28.5.
(3)中位数或众数均能反映该公司职工每人所创年利润的平均水平,
这是因为公司中少数人每人所创年利润与大多数人每人所创年利润差别较大,这样导致平均数与中位数或众数偏差较大,
所以平均数不能反映这个公司职工每人所创年利润的平均水平.
【题型强化】某大型超市抽查了100天该超市的日纯利润数据,并分成了以下几组(单位:万元):[4,5),[5,6),[6,7),[7,8),[8,9),[9,10].统计结果如表所示(统计表中每个小组取中间值作为该组数据的替代值):
组别
[4,5)
[5,6)
[6,7)
[7,8)
[8,9)
[9,10]
频数
5
20
30
30
10
5
(1)求这100天该大型超市日纯利润的平均数及中位数;
(2)利用上述样本分布估计总体分布,解决下面问题:该大型超市总经理根据每天的纯利润给员工制定了两种奖励方案:
方案一:记日纯利润为x万元,当x<6时,奖励每位员工40元/天;当6≤x<8时,奖励每位员工80元/天;当x≥8时,奖励每位员工120元/天;
方案二:日纯利润低于总体中位数时每名员工发放奖金50元/天,日纯利润不低于总体中位数时每名员工发放80元奖金/天;
“小张恰好为该大型超市的一位员工,则从统计角度看,小张选择哪种奖励方案更有利?
【解析】解:(1)这100天该大型超市日纯利涧的平均数为:(4.5×5+5.5×20+6.5×30+7.5×30+8.5×10+9.5×5)=6.85(万元),
前2组频率之和为:0.05+0.20=0.25<0.5,前3组频率之和为:0.25+0.3=0.55>0.5,故中位数位于第3组;
设中位数为t则有(t﹣6)×0.3+0.25=0.5
解得:t;
即这100天该大型超市日纯利润的中位数为万元;
(2)设选择方案一时,小张每天的奖金为x元,
则x的可能取值为40,80,120,其对应的概率分别为0.25,0.6,0.15,
所以获得奖金的平均数40×0.25+80×0.6+120×0.15=76(元)
设选择方案二时小张每天的奖金为y元
则获得奖金的平均数50×0.5+80×0.5=65(元)
因为x>y,
所以从统计角度看,小张选择方案一更有利.
【收官验收】某制造商生产长度为6cm的金属棒,抽样检查40根,测得每根长度(单位:cm,保留两位小数)如下:
6.02
6.01
5.94
5.94
5.97
5.96
5.98
6.01
5.98
5.99
6.00
6.03
5.99
5.97
5.98
6.00
6.03
5.95
6.00
6.00
5.92
5.93
5.99
5.99
6.00
5.95
6.00
5.97
5.96
5.97
6.03
6.01
5.98
5.99
6.04
6.00
6.02
5.97
5.96
5.98
(1)计算上述样本中金属棒的平均长度;
(2)画出频率分布直方图;
(3)如果允许制造商生产这种金属棒与6cm的标准有0.2%的离差,那么抽样检查中合格的金属棒有几根?合格率是多少?
【解析】解:(1)(6.02+6.01+5.94+5.94+5.97+5.96+5.98+6.01+5.98+5.99+6.00+6.03+5.99+5.97+5.98+6.00+6.03+5.95+6.00+6.00+5.92+5.93+5.99+5.99+6.00+5.95+6.00+5.97+5.96+5.97+6.03+6.01+5.98+5.99+6.04+6.00+6.02+5.97+5.96+5.98)÷40=5.99cm;
(2)频率分布表如下:
分组
频数
频率
[5.92,5.95)
4
0.1
[5.95,5.98)
10
0.25
[5.98,6.01)
17
0.425
[6.01,6.04)
9
0.225
合计
40
1
频率分布直方图如下:
(3)6×(1﹣0.2%)=5.99,6×(1+0.2%)=6.01,
故合格的金属棒有15根,合格率约为15÷40=37.5%.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
