2020-2021学年 高二物理 带电粒子在磁场中运动的临界和多解问题 期末复习强化学案Word版含答案
文档属性
| 名称 | 2020-2021学年 高二物理 带电粒子在磁场中运动的临界和多解问题 期末复习强化学案Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 482.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-14 00:00:00 | ||
图片预览




文档简介
带电粒子在磁场中运动的临界和多解问题
考点一 带电粒子在磁场中运动的临界极值问题
多维探究
解决带电粒子在磁场中的临界极值问题的关键
(1)以题目中的“恰好”“最大”“最高”“至少”等词语为突破口,运用动态思维,寻找临界点,确定临界状态,由磁场边界和题设条件画好轨迹、定好圆心,建立几何关系.
(2)寻找临界点常用的结论:
①刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切.
②当速度v一定时,弧长(或弦长)越长,圆心角越大,则带电粒子在有界磁场中运动的时间越长.
③当速度v变化时,圆心角越大,运动时间越长.
题型1|求运动时间的极值
例1 [2020·全国卷Ⅰ,18]一匀强磁场的磁感应强度大小为B,方向垂直于纸面向外,其边界如图中虚线所示,ab为半圆,ac、bd与直径ab共线,ac间的距离等于半圆的半径.一束质量为m、电荷量为q(q>0)的粒子,在纸面内从c点垂直于ac射入磁场,这些粒子具有各种速率.不计粒子之间的相互作用.在磁场中运动时间最长的粒子,其运动时间为( )
A. 7πm6qB B. 5πm4qB C. 4πm3qB D. 3πm2qB
题型2|求磁感应强度的极值
例2 [2020·全国卷Ⅲ,18]真空中有一匀强磁场,磁场边界为两个半径分别为a和3a的同轴圆柱面,磁场的方向与圆柱轴线平行,其横截面如图所示.一速率为v的电子从圆心沿半径方向进入磁场.已知电子质量为m,电荷量为e,忽略重力.为使该电子的运动被限制在图中实线圆围成的区域内,磁场的磁感应强度最小为( )
A. 3mv2ae B. mvae
C. 3mv4ae D. 3mv5ae
题型3 |求运动速度的极值
例3 如图所示,在直角三角形abc区域(含边界)内存在垂直于纸面向外的匀强磁场,磁感应强度大小为B,∠a=60°,∠b=90°,边长ac=L.一个粒子源在a点将质量为m、电荷量为q的带正电粒子以大小和方向不同的速度射入磁场,在磁场中运动时间最长的粒子中,速度的最大值是( )
A. qBL2m B. 3qBL6m C. 3qBL4m D. qBL6m
题型4|带电粒子通过磁场时的最大偏角
例4 如图所示,半径R=10 cm的圆形区域内有匀强磁场,其边界跟y轴在坐标原点O处相切,磁感强度B=0.33 T,方向垂直纸面向里.在O处有一放射源S,可沿纸面向各方向射出速率均为v=3.2×106 m/s的α粒子,已知α粒子的质量m=6.6×10-27 kg,电荷量q=3.2×10-19 C,则该α粒子通过磁场空间的最大偏转角为( )
A.30° B.45°
C.60° D.90°
题型5|求区域的长度范围
例5 如图所示,在荧光屏MN上方分布了水平方向的匀强磁场,磁感应强度的大小B=0.1 T、方向与纸面垂直.距离荧光屏h=16 cm处有一粒子源S,以速度v=1×106 m/s不断地在纸面内向各个方向发射比荷qm=1×108 C/kg的带正电粒子,不计粒子的重力.则粒子打在荧光屏范围的长度为( )
A.12 cm B.16 cm
C.20 cm D.24 cm
练1 [最小边界]
如图所示,一带电质点质量为m,电荷量为q,以平行于x轴的速度v从y轴上的a点射入图中第一象限所示的区域.为了使该质点能从x轴上的b点以垂直于x轴的速度v射出,可在适当的地方加一个垂直于xOy平面、磁感应强度为B的匀强磁场.若此磁场仅分布在一个圆形区域内,试求这圆形磁场区域的最小半径.(重力忽略不计)
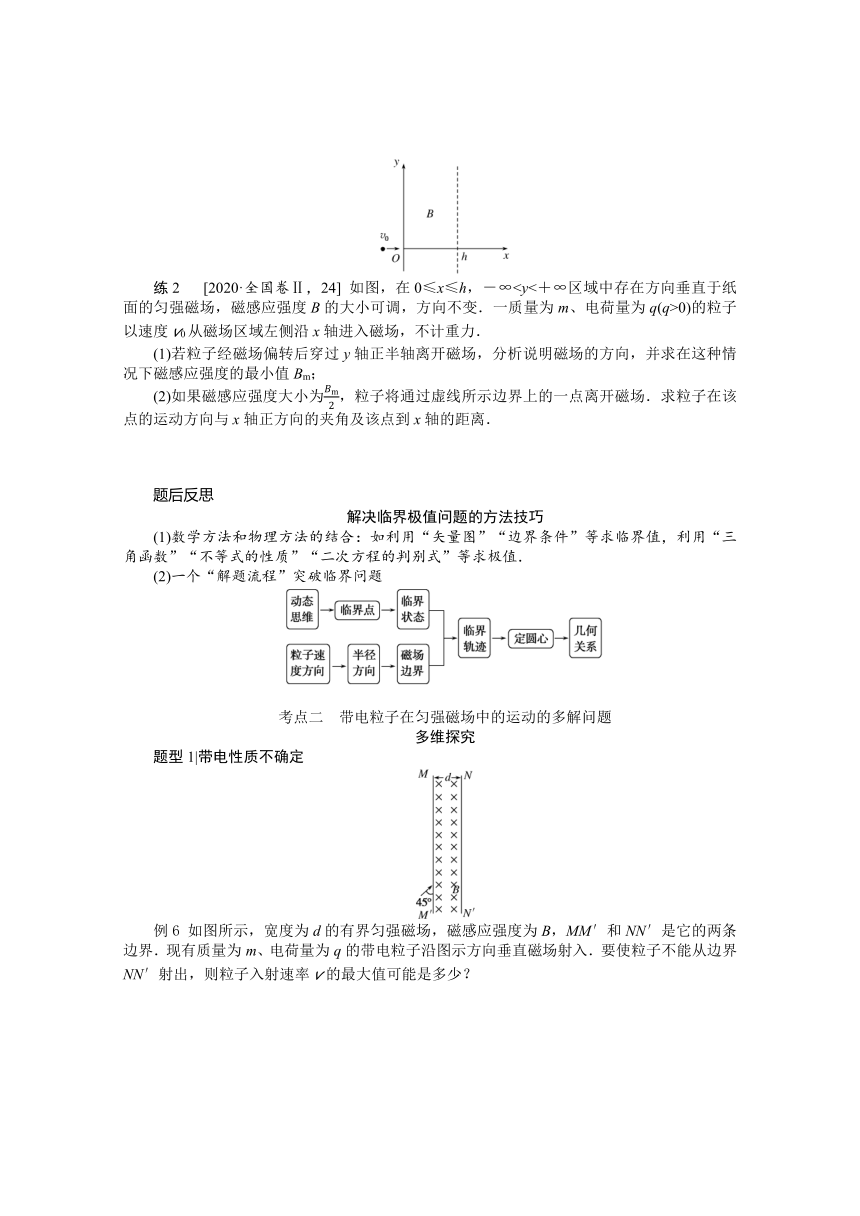
练2 [2020·全国卷Ⅱ,24] 如图,在0≤x≤h,-∞0)的粒子以速度v0从磁场区域左侧沿x轴进入磁场,不计重力.
(1)若粒子经磁场偏转后穿过y轴正半轴离开磁场,分析说明磁场的方向,并求在这种情况下磁感应强度的最小值Bm;
(2)如果磁感应强度大小为Bm2,粒子将通过虚线所示边界上的一点离开磁场.求粒子在该点的运动方向与x轴正方向的夹角及该点到x轴的距离.
题后反思
解决临界极值问题的方法技巧
(1)数学方法和物理方法的结合:如利用“矢量图”“边界条件”等求临界值,利用“三角函数”“不等式的性质”“二次方程的判别式”等求极值.
(2)一个“解题流程”突破临界问题
考点二 带电粒子在匀强磁场中的运动的多解问题
多维探究
题型1|带电性质不确定
例6 如图所示,宽度为d的有界匀强磁场,磁感应强度为B,MM′和NN′是它的两条边界.现有质量为m、电荷量为q的带电粒子沿图示方向垂直磁场射入.要使粒子不能从边界NN′射出,则粒子入射速率v的最大值可能是多少?
题型2|磁场方向不确定
例7 (多选)一质量为m,电荷量为q的负电荷在磁感应强度为B的匀强磁场中绕固定的正电荷沿固定的光滑轨道做匀速圆周运动,若磁场方向垂直于它的运动平面,且作用在负电荷的电场力恰好是磁场力的三倍,则负电荷做圆周运动的角速度可能是( )
A. 4qBm B. 3qBm C. 2qBm D. qBm
题型3|临界状态不唯一
例8 匀强磁场区域由一个半径为R的半圆和一个长为2R、宽为R2的矩形组成,磁场的方向如图所示.一束质量为m、电荷量为+q的粒子(粒子间的相互作用和重力均不计)以速度v从边界AN的中点P垂直于AN和磁场方向射入磁场中.
(1)当磁感应强度为多大时,粒子恰好从A点射出?
(2)对应于粒子可能射出的各段磁场边界,磁感应强度应满足什么条件?
题型4|带电粒子的周期性运动形成多解
解决带电粒子在磁场中的周期性运动与多解问题,关键是对运动过程进行准确分析,找出周期性运动的规律,并用数学通式表达多解性.分析运动过程要注意两点:
(1)注意磁场大小或方向的变化引起粒子运动轨迹的变化.
(2)注意粒子的运动方向改变而使粒子的运动具有周期性和对称性.
例9 [2021·广东韶关调研]如图所示,在无限长的竖直边界AC和DE间,上、下方分别充满方向垂直于平面ADEC向外的匀强磁场,上方磁场区域的磁感应强度大小为B0,OF为上、下方磁场的水平分界线.质量为m、所带电荷量为+q的粒子从AC边界上与O点相距为a的P点垂直于AC边界射入上方磁场区域,经OF上的Q点第一次进入下方磁场区域,Q点与O点的距离为3a.不考虑粒子重力.
(1)求粒子射入时的速度大小;
(2)若下方区域的磁感应强度B=3B0,粒子最终垂直于DE边界飞出,求边界DE与AC间距离的可能值.
练3 (多选)如图所示,两方向相反、磁感应强度大小均为B的匀强磁场被边长为L的等边三角形ABC理想分开,三角形内磁场垂直纸面向里,三角形顶点A处有一质子源,能沿∠BAC的角平分线发射速度不同的质子(质子重力不计),所有质子均能通过C点,质子比荷qm=k,则质子的速度可能为( )
A.2BkL B. BkL2 C. 3BkL2 D. BkL8
练4 如图所示,在平面直角坐标系xOy的第一象限y≤a范围内,存在垂直纸面向里磁感应强度为B的匀强磁场.一质量为m、电荷量为q且带负电的粒子从坐标原点O以速度大小为v0=2qBam沿不同方向射入磁场,不计粒子的重力,下列说法正确的是( )
A.若粒子初速度沿y轴正方向,则粒子在磁场中的运动时间为πm3qB
B.若粒子初速度沿y轴正方向,则粒子在磁场中的运动时间为2πm3qB
C.粒子在磁场中运动的最长时间为πm3qB
D.粒子在磁场中运动的最长时间为2πm3qB
思维拓展
“几何圆”模型在磁场临界极值问题中的应用
模型1 “放缩圆”模型的应用
适用
条件
速度方向一定,大小不同
粒子源发射速度方向一定、大小不同的带电粒子进入匀强磁场时,这些带电粒子在磁场中做匀速圆周运动的轨迹半径随速度的变化而变化
轨迹圆圆心共线
如图所示(图中只画出粒子带正电的情景),速度v越大,运动半径也越大.可以发现这些带电粒子射入磁场后,它们运动轨迹的圆心在垂直初速度方向的直线PP′上
界定
方法
以入射点P为定点,圆心位于PP′直线上,将半径放缩作轨迹圆,从而探索出临界条件,这种方法称为“放缩圆”法
例1 (多选)如图所示,正方形abcd区域内有垂直于纸面向里的匀强磁场,O点是cd边的中点.若一个带正电的粒子(重力忽略不计)从O点沿纸面以垂直于cd边的速度射入正方形内,经过时间t0刚好从c点射出磁场.现设法使该带电粒子从O点沿纸面以与Od成30°的方向(如图中虚线所示),以各种不同的速率射入正方形内,那么下列说法正确的是( )
A.该带电粒子不可能刚好从正方形的某个顶点射出磁场
B.若该带电粒子从ab边射出磁场,它在磁场中经历的时间可能是t0
C.若该带电粒子从bc边射出磁场,它在磁场中经历的时间可能是32t0
D.若该带电粒子从cd边射出磁场,它在磁场中经历的时间一定是53t0
模型2 “旋转圆”模型的应用
适用条件
速度大小
一定,方
向不同
粒子源发射速度大小一定、方向不同的带电粒子进入匀强磁场时,它们在磁场中做匀速圆周运动的半径相同,若射入初速度为v0,则轨迹半径为R=mv0qB.如图所示
轨迹圆
圆心共圆
带电粒子在磁场中做匀速圆周运动的圆心在以入射点P为圆心、半径R=mv0qB的圆上
界定方法
将一半径为R=mv0qB的圆以入射点为圆心进行旋转,从而探索粒子运动的临界条件,这种方法称为“旋转圆”法
例2 如图所示,匀强磁场垂直于纸面,磁感应强度大小为B,一群比荷为qm、速度大小为v的离子以一定发散角α由原点O出射,y轴正好平分该发散角,离子束偏转后打在x轴上长度为L的区域MN内,则cosα2为( )
A.1-BqL4mv B.12-BqL4mv C.1-BqL2mv D.1-BqLmv
专题八 带电粒子在磁场中运动的临界和多解问题
考点突破
例1 解析:如图所示,设某一粒子从磁场圆弧ab上的e点射出磁场,粒子在磁场中转过的圆心角为π+θ=π+2α,由于所有粒子在磁场中运动周期相同,粒子在磁场中做匀速圆周运动时,运动轨迹对应的圆心角越大,则运动时间越长.由几何关系可知,α最大时,ce恰好与圆弧ab相切,此时sin α=eOcO=12,可得α=π6,θ=2α=π3,设粒子在磁场中做匀速圆周运动的周期为T,粒子在磁场中运动的最长时间t=T2+T6,又T=2πmqB,解得t=4πm3qB,故选C.
答案:C
例2 解析:为使该电子的运动被限制在图中实线圆围成的区域内,且磁感应强度最小,由qvB=mv2r可知,电子在匀强磁场中的轨迹半径r=mveB,当r最大时,B最小,故临界情况为电子轨迹与有界磁场外边界相切,如图所示,由几何关系知a2+r2=(3a-r)2,解得r=43a,联立可得最小的磁感应强度B=3mv4ae,选项C正确.
答案:C
例3 解析:由分析知,粒子沿着ab边入射且运动轨迹与bc边相切时满足题意,粒子运动轨迹如图所示.由几何关系知,粒子运动轨迹半径r=ab=12L,则粒子速度的最大值v=2πrT=qBL2m,A正确.
答案:A
例4 解析:放射源发射的α粒子的速率一定,则它在匀强磁场中的轨道半径为定值,
即r=mvqB=6.6×10-27×3.2×1063.2×10-19×0.33 m=0.2 m=20 cm
α粒子在圆形磁场区的圆弧长度越大,其偏转角度也越大,而最长圆弧是两端点在圆形磁场区的直径上,又r=2R,则此圆弧所对的圆心角为60°,也就是α粒子在此圆形磁场区的最大偏转角为60°.轨迹如图所示.选项C正确.
答案:C
例5 解析:如图所示,粒子在磁场中做圆周运动的半径为R=mvqB=10 cm,若粒子打在荧光屏的左侧,当弦长等于直径时,打在荧光屏的最左侧,由几何关系有x1=2R2-h2=12 cm;粒子的运动轨迹与荧光屏右侧相切时,打在荧光屏的最右侧,由几何关系有x2=R2-h-R2=8 cm.根据数学知识可知打在荧光屏上的范围长度为x=x1+x2=12 cm+8 cm=20 cm,选项C正确.
答案:C
练1
解析:由于已知初速度与末速度的方向,可得偏向角φ=π2.设粒子由M点进入磁场,由于φ=2β,可沿粒子偏转方向β=π4来补弦MN,如图所示.
由“切线、弦”可得圆心O1,从而画轨迹弧MN.
显然M、N为磁场边界上两点,而磁场又仅分布在一圆形区域内.欲使磁场面积最小,则弦MN应为磁场边界所在圆的直径(图中虚线图),即得2r=MN.
由几何知识,在Rt△MO1O2中可知R=2r,
又因为R=mvqB,所以,这圆形磁场区域的最小半径
=22R=2mv2qB.
答案:2mv2qB
练2 解析:
(1)由题意,粒子刚进入磁场时应受到方向向上的洛伦兹力,因此磁场方向垂直于纸面向里.设粒子进入磁场中做圆周运动的半径为R,根据洛伦兹力公式和圆周运动规律,有qv0B=mv02 R①
由此可得R=mv0qB②
粒子穿过y轴正半轴离开磁场,其在磁场中做圆周运动的圆心在y轴正半轴上,半径应满足R≤h③
由题意,当磁感应强度大小为Bm时,粒子的运动半径最大,由此得Bm=mv0qh④
(2)若磁感应强度大小为Bm2,粒子做圆周运动的圆心仍在y轴正半轴上,由②④式可得,此时圆弧半径为
R′=2h⑤
粒子会穿过图中P点离开磁场,运动轨迹如图所示.设粒子在P点的运动方向与x轴正方向的夹角为α,由几何关系
sin α=h2h=12⑥
则α=π6⑦
由几何关系可得,P点与x轴的距离为
y=2h(1-cos α)⑧
联立⑦⑧式得
y=(2-3)h⑨
答案:见解析
例6
解析:题目中只给出粒子“电荷量为q”,未说明是带哪种电荷,所以分情况讨论.
若带电粒子带正电荷,则轨迹是图中与NN′相切的14圆弧,轨迹半径R=mvBq
又d=R-R·sin 45°
解得v=2+2Bqdm
若带电粒子带负电荷,则轨迹是图中与NN′相切的34圆弧,轨迹半径R′=mv'Bq
又d=R′+R′sin 45°
解得v′=2-2Bqdm
答案:(2+2)Bqdm(q为正电荷)
或(2-2)Bqdm(q为负电荷)
例7 解析:依题中条件“磁场方向垂直于它的运动平面”,磁场方向有两种可能,且这两种方向相反.在方向相反的两个匀强磁场中,由左手定则可知负电荷所受的洛伦兹力的方向也是相反的.当负电荷所受的洛伦兹力与电场力方向相同时,根据牛顿第二定律可知4Bqv=mv2R,得v=4BqRm.此种情况下,负电荷运动的角速度为ω=vR=4Bqm;当负电荷所受的洛伦兹力与电场力方向相反时,有2Bqv=mv2R,v=2BqRm,此种情况下,负电荷运动的角速度为ω=vR=2Bqm.故AC正确.
答案:AC
例8 解析:(1)由左手定则判定,粒子向左偏转,只能从PA、AC和CD三段边界射出,如图所示.当粒子从A点射出时,运动半径r1=R2.
由qvB1=mv2r1
得B1=2mvqR.
(2)当粒子从C点射出时,由勾股定理得:
(R-r2)2+R22=r22,解得r2=58R
由qvB2=mv2r2,得B2=8mv5qR
据粒子在磁场中运动半径随磁场减弱而增大,可以判断:当B>2mvqR时,粒子从PA段射出;
当8mv5qR当B<8mv5qR时,粒子从CD段射出.
答案:(1)2mvqR (2)见解析
例9 解析:(1)粒子在OF上方的运动轨迹如图甲所示,
设粒子做圆周运动的半径为R,由几何关系得
R2-(R-a)2=(3a)2,解得R=5a
由牛顿第二定律得qvB0=mv2R
解得v=5aqB0m.
(2)当B=3B0时,粒子的运动轨迹如图乙所示,粒子在OF下方的运动半径为r=53a.
设粒子的速度方向再次与射入磁场时的速度方向一致时的位置为P1,则P与P1的连线一定与OF平行,根据几何关系知PP1=4a
若粒子最终垂直于DE边界飞出,则边界DE与AC间的距离为L=nPP1=4na(n=1,2,3,…).
答案:(1)5aqB0m (2)4na(n=1,2,3,…)
练3 解析:因质子带正电,且经过C点,其可能的轨迹如图所示,所有圆弧所对圆心角均为60°,所以质子运行半径r=Ln(n=1,2,3…),由洛伦兹力提供向心力得Bqv=mv2r,即v=Bqrm=Bk·Ln(n=1,2,3…),选项B、D正确.
答案:BD
练4
解析:本题考查带电粒子在平行边界磁场中运动的临界问题.粒子运动的速度为v0=2qBam,则粒子运动的轨迹半径为r=mv0qB=2a,若粒子初速度沿y轴正方向,由几何关系知粒子在磁场中运动偏转的角度为30°,则运动时间为t1=30°360°T=112×2πrv0=πm6qB,选项A、B错误;当轨迹与磁场上边界相切时,粒子在磁场中运动的时间最长,由几何关系可知,此时粒子在磁场中偏转的角度为120°,时间为tm=120°360°T=2πm3qB,故选D.
答案:D
思维拓展
典例1
解析:由题意可知带电粒子以垂直于cd边的速度射入正方形内,经过时间t0刚好从c点射出磁场,则知带电粒子的运动周期为T=2t0.随粒子速度逐渐增大,轨迹由①→②→③→④依次渐变,由图可以知道粒子在四个边射出时,射出范围分别为OG、FE、DC、BA之间,不可能从四个顶点射出,所以A项正确;当粒子从O点沿纸面垂直于cd边射入正方形内,轨迹恰好为半个圆周,即时间t0刚好为半周期,从ab边射出的粒子所用时间小于半周期t0,从bc边射出的粒子所用时间小于23T=4t03,所有从cd边射出的粒子圆心角都是300°,所用时间为5T6=5t03,故B、C项错误,A、D项正确.
答案:AD
典例2 解析:根据洛伦兹力提供向心力,有qvB=mv2R,得R=mvqB,离子通过M、N点的轨迹如图所示,由几何关系知MN=ON-OM,过M点两圆圆心与原点连线与x轴夹角为α2,圆心在x轴上的圆在O点时的速度沿y轴正方向,由几何关系可知L=2R-2R cos α2,解得cos α2=1-BqL2mv,故选项C正确.
答案:C
考点一 带电粒子在磁场中运动的临界极值问题
多维探究
解决带电粒子在磁场中的临界极值问题的关键
(1)以题目中的“恰好”“最大”“最高”“至少”等词语为突破口,运用动态思维,寻找临界点,确定临界状态,由磁场边界和题设条件画好轨迹、定好圆心,建立几何关系.
(2)寻找临界点常用的结论:
①刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切.
②当速度v一定时,弧长(或弦长)越长,圆心角越大,则带电粒子在有界磁场中运动的时间越长.
③当速度v变化时,圆心角越大,运动时间越长.
题型1|求运动时间的极值
例1 [2020·全国卷Ⅰ,18]一匀强磁场的磁感应强度大小为B,方向垂直于纸面向外,其边界如图中虚线所示,ab为半圆,ac、bd与直径ab共线,ac间的距离等于半圆的半径.一束质量为m、电荷量为q(q>0)的粒子,在纸面内从c点垂直于ac射入磁场,这些粒子具有各种速率.不计粒子之间的相互作用.在磁场中运动时间最长的粒子,其运动时间为( )
A. 7πm6qB B. 5πm4qB C. 4πm3qB D. 3πm2qB
题型2|求磁感应强度的极值
例2 [2020·全国卷Ⅲ,18]真空中有一匀强磁场,磁场边界为两个半径分别为a和3a的同轴圆柱面,磁场的方向与圆柱轴线平行,其横截面如图所示.一速率为v的电子从圆心沿半径方向进入磁场.已知电子质量为m,电荷量为e,忽略重力.为使该电子的运动被限制在图中实线圆围成的区域内,磁场的磁感应强度最小为( )
A. 3mv2ae B. mvae
C. 3mv4ae D. 3mv5ae
题型3 |求运动速度的极值
例3 如图所示,在直角三角形abc区域(含边界)内存在垂直于纸面向外的匀强磁场,磁感应强度大小为B,∠a=60°,∠b=90°,边长ac=L.一个粒子源在a点将质量为m、电荷量为q的带正电粒子以大小和方向不同的速度射入磁场,在磁场中运动时间最长的粒子中,速度的最大值是( )
A. qBL2m B. 3qBL6m C. 3qBL4m D. qBL6m
题型4|带电粒子通过磁场时的最大偏角
例4 如图所示,半径R=10 cm的圆形区域内有匀强磁场,其边界跟y轴在坐标原点O处相切,磁感强度B=0.33 T,方向垂直纸面向里.在O处有一放射源S,可沿纸面向各方向射出速率均为v=3.2×106 m/s的α粒子,已知α粒子的质量m=6.6×10-27 kg,电荷量q=3.2×10-19 C,则该α粒子通过磁场空间的最大偏转角为( )
A.30° B.45°
C.60° D.90°
题型5|求区域的长度范围
例5 如图所示,在荧光屏MN上方分布了水平方向的匀强磁场,磁感应强度的大小B=0.1 T、方向与纸面垂直.距离荧光屏h=16 cm处有一粒子源S,以速度v=1×106 m/s不断地在纸面内向各个方向发射比荷qm=1×108 C/kg的带正电粒子,不计粒子的重力.则粒子打在荧光屏范围的长度为( )
A.12 cm B.16 cm
C.20 cm D.24 cm
练1 [最小边界]
如图所示,一带电质点质量为m,电荷量为q,以平行于x轴的速度v从y轴上的a点射入图中第一象限所示的区域.为了使该质点能从x轴上的b点以垂直于x轴的速度v射出,可在适当的地方加一个垂直于xOy平面、磁感应强度为B的匀强磁场.若此磁场仅分布在一个圆形区域内,试求这圆形磁场区域的最小半径.(重力忽略不计)
练2 [2020·全国卷Ⅱ,24] 如图,在0≤x≤h,-∞
(1)若粒子经磁场偏转后穿过y轴正半轴离开磁场,分析说明磁场的方向,并求在这种情况下磁感应强度的最小值Bm;
(2)如果磁感应强度大小为Bm2,粒子将通过虚线所示边界上的一点离开磁场.求粒子在该点的运动方向与x轴正方向的夹角及该点到x轴的距离.
题后反思
解决临界极值问题的方法技巧
(1)数学方法和物理方法的结合:如利用“矢量图”“边界条件”等求临界值,利用“三角函数”“不等式的性质”“二次方程的判别式”等求极值.
(2)一个“解题流程”突破临界问题
考点二 带电粒子在匀强磁场中的运动的多解问题
多维探究
题型1|带电性质不确定
例6 如图所示,宽度为d的有界匀强磁场,磁感应强度为B,MM′和NN′是它的两条边界.现有质量为m、电荷量为q的带电粒子沿图示方向垂直磁场射入.要使粒子不能从边界NN′射出,则粒子入射速率v的最大值可能是多少?
题型2|磁场方向不确定
例7 (多选)一质量为m,电荷量为q的负电荷在磁感应强度为B的匀强磁场中绕固定的正电荷沿固定的光滑轨道做匀速圆周运动,若磁场方向垂直于它的运动平面,且作用在负电荷的电场力恰好是磁场力的三倍,则负电荷做圆周运动的角速度可能是( )
A. 4qBm B. 3qBm C. 2qBm D. qBm
题型3|临界状态不唯一
例8 匀强磁场区域由一个半径为R的半圆和一个长为2R、宽为R2的矩形组成,磁场的方向如图所示.一束质量为m、电荷量为+q的粒子(粒子间的相互作用和重力均不计)以速度v从边界AN的中点P垂直于AN和磁场方向射入磁场中.
(1)当磁感应强度为多大时,粒子恰好从A点射出?
(2)对应于粒子可能射出的各段磁场边界,磁感应强度应满足什么条件?
题型4|带电粒子的周期性运动形成多解
解决带电粒子在磁场中的周期性运动与多解问题,关键是对运动过程进行准确分析,找出周期性运动的规律,并用数学通式表达多解性.分析运动过程要注意两点:
(1)注意磁场大小或方向的变化引起粒子运动轨迹的变化.
(2)注意粒子的运动方向改变而使粒子的运动具有周期性和对称性.
例9 [2021·广东韶关调研]如图所示,在无限长的竖直边界AC和DE间,上、下方分别充满方向垂直于平面ADEC向外的匀强磁场,上方磁场区域的磁感应强度大小为B0,OF为上、下方磁场的水平分界线.质量为m、所带电荷量为+q的粒子从AC边界上与O点相距为a的P点垂直于AC边界射入上方磁场区域,经OF上的Q点第一次进入下方磁场区域,Q点与O点的距离为3a.不考虑粒子重力.
(1)求粒子射入时的速度大小;
(2)若下方区域的磁感应强度B=3B0,粒子最终垂直于DE边界飞出,求边界DE与AC间距离的可能值.
练3 (多选)如图所示,两方向相反、磁感应强度大小均为B的匀强磁场被边长为L的等边三角形ABC理想分开,三角形内磁场垂直纸面向里,三角形顶点A处有一质子源,能沿∠BAC的角平分线发射速度不同的质子(质子重力不计),所有质子均能通过C点,质子比荷qm=k,则质子的速度可能为( )
A.2BkL B. BkL2 C. 3BkL2 D. BkL8
练4 如图所示,在平面直角坐标系xOy的第一象限y≤a范围内,存在垂直纸面向里磁感应强度为B的匀强磁场.一质量为m、电荷量为q且带负电的粒子从坐标原点O以速度大小为v0=2qBam沿不同方向射入磁场,不计粒子的重力,下列说法正确的是( )
A.若粒子初速度沿y轴正方向,则粒子在磁场中的运动时间为πm3qB
B.若粒子初速度沿y轴正方向,则粒子在磁场中的运动时间为2πm3qB
C.粒子在磁场中运动的最长时间为πm3qB
D.粒子在磁场中运动的最长时间为2πm3qB
思维拓展
“几何圆”模型在磁场临界极值问题中的应用
模型1 “放缩圆”模型的应用
适用
条件
速度方向一定,大小不同
粒子源发射速度方向一定、大小不同的带电粒子进入匀强磁场时,这些带电粒子在磁场中做匀速圆周运动的轨迹半径随速度的变化而变化
轨迹圆圆心共线
如图所示(图中只画出粒子带正电的情景),速度v越大,运动半径也越大.可以发现这些带电粒子射入磁场后,它们运动轨迹的圆心在垂直初速度方向的直线PP′上
界定
方法
以入射点P为定点,圆心位于PP′直线上,将半径放缩作轨迹圆,从而探索出临界条件,这种方法称为“放缩圆”法
例1 (多选)如图所示,正方形abcd区域内有垂直于纸面向里的匀强磁场,O点是cd边的中点.若一个带正电的粒子(重力忽略不计)从O点沿纸面以垂直于cd边的速度射入正方形内,经过时间t0刚好从c点射出磁场.现设法使该带电粒子从O点沿纸面以与Od成30°的方向(如图中虚线所示),以各种不同的速率射入正方形内,那么下列说法正确的是( )
A.该带电粒子不可能刚好从正方形的某个顶点射出磁场
B.若该带电粒子从ab边射出磁场,它在磁场中经历的时间可能是t0
C.若该带电粒子从bc边射出磁场,它在磁场中经历的时间可能是32t0
D.若该带电粒子从cd边射出磁场,它在磁场中经历的时间一定是53t0
模型2 “旋转圆”模型的应用
适用条件
速度大小
一定,方
向不同
粒子源发射速度大小一定、方向不同的带电粒子进入匀强磁场时,它们在磁场中做匀速圆周运动的半径相同,若射入初速度为v0,则轨迹半径为R=mv0qB.如图所示
轨迹圆
圆心共圆
带电粒子在磁场中做匀速圆周运动的圆心在以入射点P为圆心、半径R=mv0qB的圆上
界定方法
将一半径为R=mv0qB的圆以入射点为圆心进行旋转,从而探索粒子运动的临界条件,这种方法称为“旋转圆”法
例2 如图所示,匀强磁场垂直于纸面,磁感应强度大小为B,一群比荷为qm、速度大小为v的离子以一定发散角α由原点O出射,y轴正好平分该发散角,离子束偏转后打在x轴上长度为L的区域MN内,则cosα2为( )
A.1-BqL4mv B.12-BqL4mv C.1-BqL2mv D.1-BqLmv
专题八 带电粒子在磁场中运动的临界和多解问题
考点突破
例1 解析:如图所示,设某一粒子从磁场圆弧ab上的e点射出磁场,粒子在磁场中转过的圆心角为π+θ=π+2α,由于所有粒子在磁场中运动周期相同,粒子在磁场中做匀速圆周运动时,运动轨迹对应的圆心角越大,则运动时间越长.由几何关系可知,α最大时,ce恰好与圆弧ab相切,此时sin α=eOcO=12,可得α=π6,θ=2α=π3,设粒子在磁场中做匀速圆周运动的周期为T,粒子在磁场中运动的最长时间t=T2+T6,又T=2πmqB,解得t=4πm3qB,故选C.
答案:C
例2 解析:为使该电子的运动被限制在图中实线圆围成的区域内,且磁感应强度最小,由qvB=mv2r可知,电子在匀强磁场中的轨迹半径r=mveB,当r最大时,B最小,故临界情况为电子轨迹与有界磁场外边界相切,如图所示,由几何关系知a2+r2=(3a-r)2,解得r=43a,联立可得最小的磁感应强度B=3mv4ae,选项C正确.
答案:C
例3 解析:由分析知,粒子沿着ab边入射且运动轨迹与bc边相切时满足题意,粒子运动轨迹如图所示.由几何关系知,粒子运动轨迹半径r=ab=12L,则粒子速度的最大值v=2πrT=qBL2m,A正确.
答案:A
例4 解析:放射源发射的α粒子的速率一定,则它在匀强磁场中的轨道半径为定值,
即r=mvqB=6.6×10-27×3.2×1063.2×10-19×0.33 m=0.2 m=20 cm
α粒子在圆形磁场区的圆弧长度越大,其偏转角度也越大,而最长圆弧是两端点在圆形磁场区的直径上,又r=2R,则此圆弧所对的圆心角为60°,也就是α粒子在此圆形磁场区的最大偏转角为60°.轨迹如图所示.选项C正确.
答案:C
例5 解析:如图所示,粒子在磁场中做圆周运动的半径为R=mvqB=10 cm,若粒子打在荧光屏的左侧,当弦长等于直径时,打在荧光屏的最左侧,由几何关系有x1=2R2-h2=12 cm;粒子的运动轨迹与荧光屏右侧相切时,打在荧光屏的最右侧,由几何关系有x2=R2-h-R2=8 cm.根据数学知识可知打在荧光屏上的范围长度为x=x1+x2=12 cm+8 cm=20 cm,选项C正确.
答案:C
练1
解析:由于已知初速度与末速度的方向,可得偏向角φ=π2.设粒子由M点进入磁场,由于φ=2β,可沿粒子偏转方向β=π4来补弦MN,如图所示.
由“切线、弦”可得圆心O1,从而画轨迹弧MN.
显然M、N为磁场边界上两点,而磁场又仅分布在一圆形区域内.欲使磁场面积最小,则弦MN应为磁场边界所在圆的直径(图中虚线图),即得2r=MN.
由几何知识,在Rt△MO1O2中可知R=2r,
又因为R=mvqB,所以,这圆形磁场区域的最小半径
=22R=2mv2qB.
答案:2mv2qB
练2 解析:
(1)由题意,粒子刚进入磁场时应受到方向向上的洛伦兹力,因此磁场方向垂直于纸面向里.设粒子进入磁场中做圆周运动的半径为R,根据洛伦兹力公式和圆周运动规律,有qv0B=mv02 R①
由此可得R=mv0qB②
粒子穿过y轴正半轴离开磁场,其在磁场中做圆周运动的圆心在y轴正半轴上,半径应满足R≤h③
由题意,当磁感应强度大小为Bm时,粒子的运动半径最大,由此得Bm=mv0qh④
(2)若磁感应强度大小为Bm2,粒子做圆周运动的圆心仍在y轴正半轴上,由②④式可得,此时圆弧半径为
R′=2h⑤
粒子会穿过图中P点离开磁场,运动轨迹如图所示.设粒子在P点的运动方向与x轴正方向的夹角为α,由几何关系
sin α=h2h=12⑥
则α=π6⑦
由几何关系可得,P点与x轴的距离为
y=2h(1-cos α)⑧
联立⑦⑧式得
y=(2-3)h⑨
答案:见解析
例6
解析:题目中只给出粒子“电荷量为q”,未说明是带哪种电荷,所以分情况讨论.
若带电粒子带正电荷,则轨迹是图中与NN′相切的14圆弧,轨迹半径R=mvBq
又d=R-R·sin 45°
解得v=2+2Bqdm
若带电粒子带负电荷,则轨迹是图中与NN′相切的34圆弧,轨迹半径R′=mv'Bq
又d=R′+R′sin 45°
解得v′=2-2Bqdm
答案:(2+2)Bqdm(q为正电荷)
或(2-2)Bqdm(q为负电荷)
例7 解析:依题中条件“磁场方向垂直于它的运动平面”,磁场方向有两种可能,且这两种方向相反.在方向相反的两个匀强磁场中,由左手定则可知负电荷所受的洛伦兹力的方向也是相反的.当负电荷所受的洛伦兹力与电场力方向相同时,根据牛顿第二定律可知4Bqv=mv2R,得v=4BqRm.此种情况下,负电荷运动的角速度为ω=vR=4Bqm;当负电荷所受的洛伦兹力与电场力方向相反时,有2Bqv=mv2R,v=2BqRm,此种情况下,负电荷运动的角速度为ω=vR=2Bqm.故AC正确.
答案:AC
例8 解析:(1)由左手定则判定,粒子向左偏转,只能从PA、AC和CD三段边界射出,如图所示.当粒子从A点射出时,运动半径r1=R2.
由qvB1=mv2r1
得B1=2mvqR.
(2)当粒子从C点射出时,由勾股定理得:
(R-r2)2+R22=r22,解得r2=58R
由qvB2=mv2r2,得B2=8mv5qR
据粒子在磁场中运动半径随磁场减弱而增大,可以判断:当B>2mvqR时,粒子从PA段射出;
当8mv5qR
答案:(1)2mvqR (2)见解析
例9 解析:(1)粒子在OF上方的运动轨迹如图甲所示,
设粒子做圆周运动的半径为R,由几何关系得
R2-(R-a)2=(3a)2,解得R=5a
由牛顿第二定律得qvB0=mv2R
解得v=5aqB0m.
(2)当B=3B0时,粒子的运动轨迹如图乙所示,粒子在OF下方的运动半径为r=53a.
设粒子的速度方向再次与射入磁场时的速度方向一致时的位置为P1,则P与P1的连线一定与OF平行,根据几何关系知PP1=4a
若粒子最终垂直于DE边界飞出,则边界DE与AC间的距离为L=nPP1=4na(n=1,2,3,…).
答案:(1)5aqB0m (2)4na(n=1,2,3,…)
练3 解析:因质子带正电,且经过C点,其可能的轨迹如图所示,所有圆弧所对圆心角均为60°,所以质子运行半径r=Ln(n=1,2,3…),由洛伦兹力提供向心力得Bqv=mv2r,即v=Bqrm=Bk·Ln(n=1,2,3…),选项B、D正确.
答案:BD
练4
解析:本题考查带电粒子在平行边界磁场中运动的临界问题.粒子运动的速度为v0=2qBam,则粒子运动的轨迹半径为r=mv0qB=2a,若粒子初速度沿y轴正方向,由几何关系知粒子在磁场中运动偏转的角度为30°,则运动时间为t1=30°360°T=112×2πrv0=πm6qB,选项A、B错误;当轨迹与磁场上边界相切时,粒子在磁场中运动的时间最长,由几何关系可知,此时粒子在磁场中偏转的角度为120°,时间为tm=120°360°T=2πm3qB,故选D.
答案:D
思维拓展
典例1
解析:由题意可知带电粒子以垂直于cd边的速度射入正方形内,经过时间t0刚好从c点射出磁场,则知带电粒子的运动周期为T=2t0.随粒子速度逐渐增大,轨迹由①→②→③→④依次渐变,由图可以知道粒子在四个边射出时,射出范围分别为OG、FE、DC、BA之间,不可能从四个顶点射出,所以A项正确;当粒子从O点沿纸面垂直于cd边射入正方形内,轨迹恰好为半个圆周,即时间t0刚好为半周期,从ab边射出的粒子所用时间小于半周期t0,从bc边射出的粒子所用时间小于23T=4t03,所有从cd边射出的粒子圆心角都是300°,所用时间为5T6=5t03,故B、C项错误,A、D项正确.
答案:AD
典例2 解析:根据洛伦兹力提供向心力,有qvB=mv2R,得R=mvqB,离子通过M、N点的轨迹如图所示,由几何关系知MN=ON-OM,过M点两圆圆心与原点连线与x轴夹角为α2,圆心在x轴上的圆在O点时的速度沿y轴正方向,由几何关系可知L=2R-2R cos α2,解得cos α2=1-BqL2mv,故选项C正确.
答案:C
同课章节目录
