2020-2021学年七年级数学北师大版 下册 第5章生活中的轴对称易错题专题突破训练2(附答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版 下册 第5章生活中的轴对称易错题专题突破训练2(附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 258.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 11:01:54 | ||
图片预览



文档简介
2021年北师大版七年级数学下册第5章生活中的轴对称易错题专题突破训练2(附答案)
1.如图,在△ABC中,DE垂直平分AC,若BC=22cm,AB=14cm,则△ABD的周长为( )
A.24cm B.25cm C.30cm D.36cm
2.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A.13 B.17 C.13或17 D.13或10
3.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法不正确的是( )
A.△ABE的面积=△BCE的面积 B.∠AFG=∠AGF
C.BH=CH D.∠FAG=2∠ACF
4.如图,在△ABC中AB=AC,∠BAC=120°,点D、E在边BC,且∠BAE=∠DAC=90°,图中等腰三角形有( )
A.2个 B.4个 C.6个 D.8个
5.若一个三角形的最小内角为60°,则下列判断中正确的有( )
(1)这个三角形是锐角三角形;(2)这个三角形是等腰三角形;(3)这个三角形是等边三角形;(4)形状不能确定;(5)不存在这样的三角形.
A.1个 B.2个 C.3个 D.4个
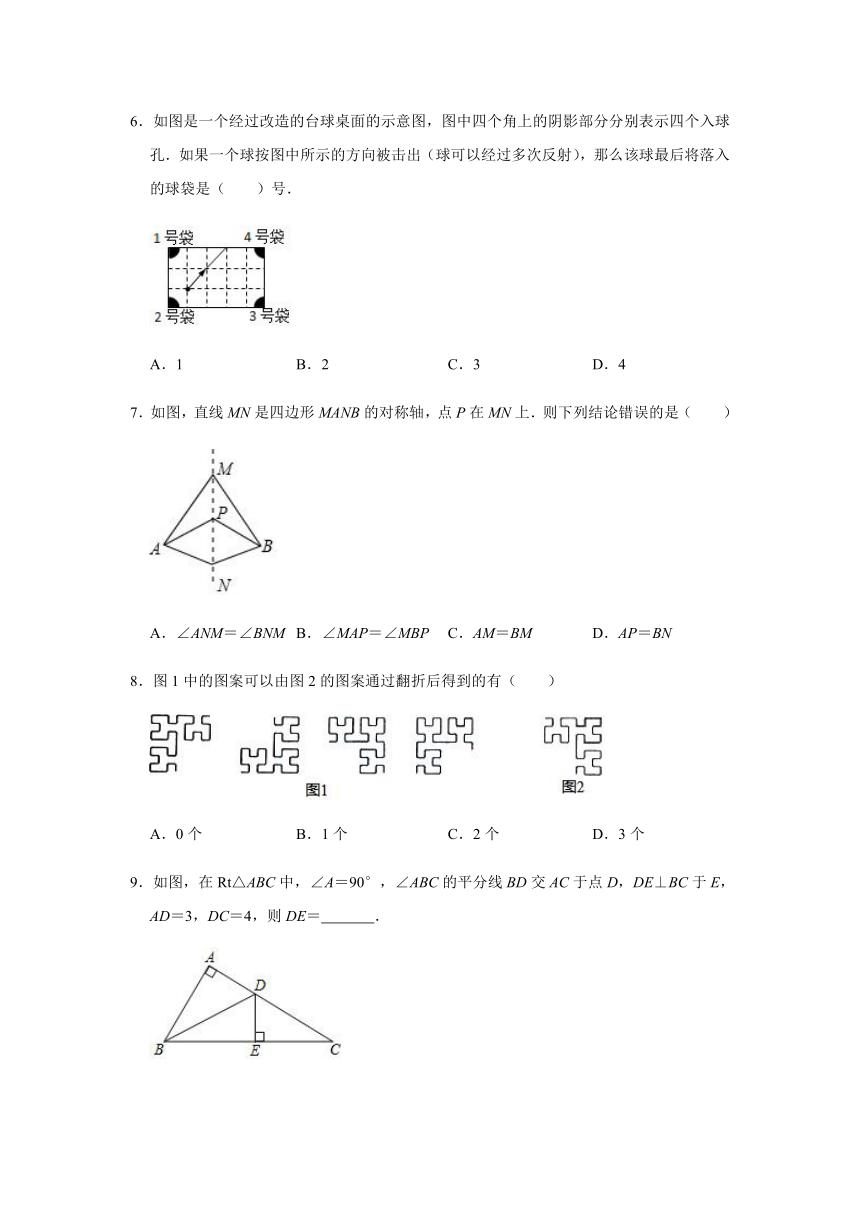
6.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1 B.2 C.3 D.4
7.如图,直线MN是四边形MANB的对称轴,点P在MN上.则下列结论错误的是( )
A.∠ANM=∠BNM B.∠MAP=∠MBP C.AM=BM D.AP=BN
8.图1中的图案可以由图2的图案通过翻折后得到的有( )
A.0个 B.1个 C.2个 D.3个
9.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,DE⊥BC于E,AD=3,DC=4,则DE= .
10.如图,在△ABC中,DE是AC的中垂线,△ABD的周长为17cm,AE=5cm,则△ABC的周长是 .
11.若等腰三角形的一个外角是110°,则其底角为 .
12.如图,线段OA的长为2,它的一个端点O是数轴的原点,OA与数轴正半轴的夹角为45度,以OA为一边作等腰三角形OAB,使顶点B在数轴上,则数轴上点B所表示的数是 .
13.如图,等边△ABC的边长为l,取边AC的中点D,在外部画出一个新的等边三角形△CDE,如此绕点C顺时针继续下去,直到所画等边三角形的一边与△ABC的BC边重叠为止,此时这个三角形的边长为 .
14.如图,已知△ABC是等边三角形,D是BC边上的一个动点(异于点B、C),过点D作DE⊥AB,垂足为E,DE的垂直平分线分别交AC、BC于点F、G,连接FD,FE.当点D在BC边上移动时,有下列三个结论:①△DEF一定为等腰三角形,②△CFG一定为等边三角形,③△FDC可能为等腰三角形.其中正确的是 .(填写序号)
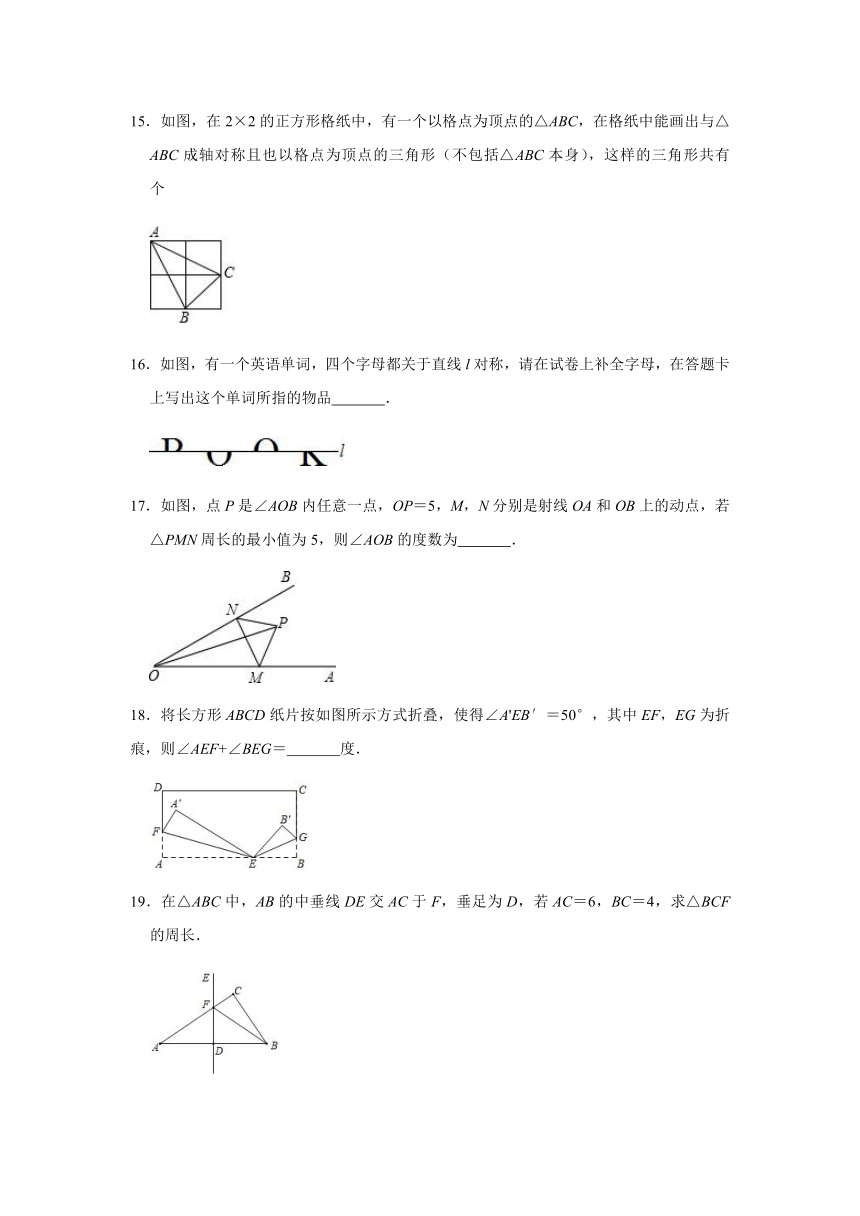
15.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,在格纸中能画出与△ABC成轴对称且也以格点为顶点的三角形(不包括△ABC本身),这样的三角形共有 个
16.如图,有一个英语单词,四个字母都关于直线l对称,请在试卷上补全字母,在答题卡上写出这个单词所指的物品 .
17.如图,点P是∠AOB内任意一点,OP=5,M,N分别是射线OA和OB上的动点,若△PMN周长的最小值为5,则∠AOB的度数为 .
18.将长方形ABCD纸片按如图所示方式折叠,使得∠A'EB′=50°,其中EF,EG为折痕,则∠AEF+∠BEG= 度.
19.在△ABC中,AB的中垂线DE交AC于F,垂足为D,若AC=6,BC=4,求△BCF的周长.
20.如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点.求CD的长.
21.小明用一条长30cm的细绳围成了一个等腰三角形,他想使这个三角形的一边长是另一边长的2倍,那么这个三角形的各边的长分别是多少?
22.已知一个三角形可以被分成两个等腰三角形.若原三角形的一个内角为36°,求原三角形的最大内角的所有可能值.
23.如图,BD是△ABC的角平分线,DE∥BC交AB于点E,EF∥AC,EF分别交BC、BD于点F、G.
(1)求证:BE=CF;
(2)若AE=BE,在不添加任何辅助线的情况下,请直接写出图中所有的直角三角形.
24.扇形是轴对称图形吗?设计一个方案验证自己的猜测.
25.如图,在平面直角坐标系中有一个△ABC,点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
26.已知△ABC在平面直角坐标系中的位置如图所示,
(1)先画出△ABC关于x轴对称的图形△A1B1C1,再画出△A1B1C1关于y轴对称的图形△A2B2C2;
(2)直接写出△A2B2C2各顶点的坐标.
27.如图,在正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,网格中有一个格点△ABC即三角形的顶点都在格点上.
(1)在图中作出△ABC关于直线l对称的△A1B1C1
(要求A与A1,B与B1,C与C1相对应)
(2)△ABC的面积为 .
(3)在直线l上找一点P,使得PA+PC的和最小.
参考答案
1.解:∵DE垂直平分AC,
∴DA=DC,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=36(cm).
故选:D.
2.解:①当腰是3,底边是7时,不满足三角形的三边关系,因此舍去.
②当底边是3,腰长是7时,能构成三角形,则其周长=3+7+7=17.
故选:B.
3.解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故A正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故B正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故D正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故C错误;
故选:C.
4.解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
又∵∠BAE=∠DAC=90°,
∴∠AEB=∠ADC=60°,
∴∠BAD=∠EAC=30°,
∴图中等腰三角形有△ABC,△ABD,△ACE,△ADE,
故选:B.
5.解:因为最小角为60度,则该三角形的最大角不能大于60度,否则不合题意,则可以得到其三个角均为60度,即是一个等边三角形;
其最大角不大于90度,所以是锐角三角形;
等边三角形是特殊的等腰三角形.
所以前三项正确,即正确有三个.
故选:C.
6.解:根据轴对称的性质可知,台球走过的路径为:
∴该球最后将落入的球袋是4号.
故选:D.
7.解:∵直线MN是四边形AMBN的对称轴,
∴点A与点B对应,
∴AM=BM,AN=BN,∠ANM=∠BNM,
∵点P是直线MN上的点,
∴∠MAP=∠MBP,
∴A,B,C正确,而D错误,
故选:D.
8.解:观察图案可知:
具有轴对称性质的图案只有2个,
第二个需要图2上下翻折可得,
第1个需要左右翻折可得.
故选:C.
9.解:∵∠A=90°,
∴DA⊥BA,
又∵BD是∠ABC的平分线,DE⊥BC,
∴DE=AD,
∵AD=3,
∴DE=3,
故答案为:3.
10.解:∵DE是AC的垂直平分线,
∴DA=DC,AE=EC=5cm,
又∵△ABD的周长为17cm,即AB+BD+AD=17cm,
∴AB+BD+DC=17cm,
∴AB+BC+AC=17+10=27(cm),
即△ABC的周长为27cm.
故答案为:27cm.
11.解:
当110°外角为底角的外角时,则其底角为:180°﹣110°=70°;
当110°外角为顶角的外角时,则其顶角为:70°,则其底角为:=55°,
故答案为:70°或55°.
12.解:如图,在数轴上取点B1,B2,B3,B4,
使OB1=OA=2,OB3=OA=2,AB4=OA=2,
根据题意可知:
OA=2,∠AOB2=45°,
作AB2⊥x轴于点B2,
则OB2=AB2=,
∴OB4=2,
∴数轴上点B所表示的数是:﹣2,,2,2.
故答案为:﹣2或或2或2.
13.解:∵要使所画三角形的一边与BC重合,
∴应顺时针方向再作5个三角形,
∴其边长为1×()5=.
∴这个三角形的边长为.
故填.
14.解:∵DE的垂直平分线分别交AC、BC于点F、G,
∴FE=FD,
∴△DEF为等腰三角形,故①正确;
∵DE⊥AB,DE⊥FG,
∴AB∥FG,
∴∠FGC=∠B=60°,
又∵△ABC是等边三角形,
∴∠C=60°,
∴△CFG中,∠C=∠CFG=∠CGF,
∴△CFG是等边三角形,故②正确;
∵∠FDC>∠FGC=60°,∠C=60°,∠CFD<∠CFG=60°,
∴△CDF不可能是等腰三角形,故③错误;
故答案为:①②.
15.解:如图所示,与△ABC成轴对称且也以格点为顶点的三角形有3个:
故答案为:3.
16.解:如图,
这个单词所指的物品是书.
故答案为:书.
17.解:分别作点P关于OB、AO的对称点P′、P″
分别连OP′、OP″、P′P″交OB、OA于M、N
由轴对称△PMN周长等于PN+NM+MP=P′N+NM+MP″=P′P″
∴由两点之间线段最短可知,此时△PMN周长的最小
∴P′P″=5
由对称OP=OP′=OP″=5
∴△P′OP″为等边三角形
∴∠P′OP″=60°
∵∠P′OB=∠POB,∠P″OA=∠POA
∴∠AOB=∠P′OP″=30°.
故答案为:30°.
18.解:由折叠可得,∠AEF=∠AEA',∠BEG=∠BEB',
∵∠A'EB′=50°,
∴∠AEA'+∠BEB'=130°,
∴∠AEF+∠BEG=(∠AEA'+∠BEB')=130°=65°,
故答案为:65.
19.解:∵AB的中垂线DE交AC于F,
∴AF=BF.
又∵AC=6,BC=4,
∴△BCF的周长=BC+CF+FB=BC+CF+FA=BC+AC=10.
20.解:∵DE是AC的垂直平分线,
∴CD=AD,
∴AB=BD+AD=BD+CD,
设CD=x,则BD=4﹣x,
在Rt△BCD中,
CD2=BC2+BD2,即x2=32+(4﹣x)2,
解得x=.
所以CD的长为:.
21.解:设一边为xcm,则另一边为2xcm,
当长为xcm的边为腰时,此时三角形的三边长分别为xcm、xcm、2xcm,
由题意可列方程:x+x+2x=30,解得x=7.5,此时三角形的三边长分别为:7.5、7.5和15,因为7.5+7.5=15,不符合三角形三边之间的关系,所以不符合题意;
当长为xcm的边为底时,此时三角形的三边长分别为xcm、2xcm、2xcm,
由题意可列方程:x+2x+2x=30,解得x=6,此时三角形的三边长分别为:6、12、12,满足三角形的三边之间的关系,
所以这个三角形的各边长分别为6cm、12cm和12cm.
22.解:①原三角形是锐角三角形,最大角是72°的情况:
如图∠ABC=∠ACB=72°,∠A=36°,AD=BD=BC,则最大角是72°;
,
②原三角形是直角三角形,最大角是90°的情况:
如图∠ABC=90°,∠A=36°,AD=CD=BD,;
③原三角形是钝角三角形,最大角是108°的情况:
如图∠BAC=108°,∠B=36°,BD=AB,AD=DC,
④原三角形是钝角三角形,最大角是126°的情况:
如图∠ABC=126°,∠C=36°,AD=BD=BC,
⑤原三角形是钝角三角形,最大角是132°的情况:
如图∠C=132°,∠ABC=36°,AD=BD,CD=CB,
故答案为:72°,90°,108°,132°,126°.
23.解:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC,
∵DE∥BC,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴BE=DE,
∵DE∥BC,EF∥AC,
∴四边形EFCD是平行四边形,
∴DE=CF,
∴BE=CF.
(2)若AE=BE,则AE=DE=BE,
∴∠A=∠ADE,∠EBD=∠EDB,
又∵∠A+∠ADE+∠EDB+∠EBD=180°,
∴∠ADE+∠EDB=90°,即BD⊥AC,
又∵EF∥AC,
∴BD⊥EF,
∴图中的直角三角形为:△ABD,△CBD,△BEG,△BFG,△DEG.
24.解:根据题意,扇形是轴对称图形,它有1条对称轴.
设计方案如下:
如图,将扇形沿圆心角的角平分线所在直线折叠,两边重合,所以扇形是轴对称图形.
25.解:(1)如图所示;
(2)S△ABC=4×5﹣×2×4﹣×3×3﹣×1×5
=20﹣4﹣﹣
=9.
故答案为:9.
26.解:(1)如图所示,△A1B1C1,△A2B2C2即为所求;
(2)如图所示,A2(﹣5,﹣5),B2(﹣2,﹣3),C2(﹣4,﹣2).
27.解:(1)如图所示:△A1B1C1即为所求;
(2)△ABC的面积为:3×4﹣×2×3+×2×2﹣×1×4=5;
故答案为:5;
(3)如图所示:点P即为所求的点.
1.如图,在△ABC中,DE垂直平分AC,若BC=22cm,AB=14cm,则△ABD的周长为( )
A.24cm B.25cm C.30cm D.36cm
2.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A.13 B.17 C.13或17 D.13或10
3.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法不正确的是( )
A.△ABE的面积=△BCE的面积 B.∠AFG=∠AGF
C.BH=CH D.∠FAG=2∠ACF
4.如图,在△ABC中AB=AC,∠BAC=120°,点D、E在边BC,且∠BAE=∠DAC=90°,图中等腰三角形有( )
A.2个 B.4个 C.6个 D.8个
5.若一个三角形的最小内角为60°,则下列判断中正确的有( )
(1)这个三角形是锐角三角形;(2)这个三角形是等腰三角形;(3)这个三角形是等边三角形;(4)形状不能确定;(5)不存在这样的三角形.
A.1个 B.2个 C.3个 D.4个
6.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )号.
A.1 B.2 C.3 D.4
7.如图,直线MN是四边形MANB的对称轴,点P在MN上.则下列结论错误的是( )
A.∠ANM=∠BNM B.∠MAP=∠MBP C.AM=BM D.AP=BN
8.图1中的图案可以由图2的图案通过翻折后得到的有( )
A.0个 B.1个 C.2个 D.3个
9.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,DE⊥BC于E,AD=3,DC=4,则DE= .
10.如图,在△ABC中,DE是AC的中垂线,△ABD的周长为17cm,AE=5cm,则△ABC的周长是 .
11.若等腰三角形的一个外角是110°,则其底角为 .
12.如图,线段OA的长为2,它的一个端点O是数轴的原点,OA与数轴正半轴的夹角为45度,以OA为一边作等腰三角形OAB,使顶点B在数轴上,则数轴上点B所表示的数是 .
13.如图,等边△ABC的边长为l,取边AC的中点D,在外部画出一个新的等边三角形△CDE,如此绕点C顺时针继续下去,直到所画等边三角形的一边与△ABC的BC边重叠为止,此时这个三角形的边长为 .
14.如图,已知△ABC是等边三角形,D是BC边上的一个动点(异于点B、C),过点D作DE⊥AB,垂足为E,DE的垂直平分线分别交AC、BC于点F、G,连接FD,FE.当点D在BC边上移动时,有下列三个结论:①△DEF一定为等腰三角形,②△CFG一定为等边三角形,③△FDC可能为等腰三角形.其中正确的是 .(填写序号)
15.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,在格纸中能画出与△ABC成轴对称且也以格点为顶点的三角形(不包括△ABC本身),这样的三角形共有 个
16.如图,有一个英语单词,四个字母都关于直线l对称,请在试卷上补全字母,在答题卡上写出这个单词所指的物品 .
17.如图,点P是∠AOB内任意一点,OP=5,M,N分别是射线OA和OB上的动点,若△PMN周长的最小值为5,则∠AOB的度数为 .
18.将长方形ABCD纸片按如图所示方式折叠,使得∠A'EB′=50°,其中EF,EG为折痕,则∠AEF+∠BEG= 度.
19.在△ABC中,AB的中垂线DE交AC于F,垂足为D,若AC=6,BC=4,求△BCF的周长.
20.如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点.求CD的长.
21.小明用一条长30cm的细绳围成了一个等腰三角形,他想使这个三角形的一边长是另一边长的2倍,那么这个三角形的各边的长分别是多少?
22.已知一个三角形可以被分成两个等腰三角形.若原三角形的一个内角为36°,求原三角形的最大内角的所有可能值.
23.如图,BD是△ABC的角平分线,DE∥BC交AB于点E,EF∥AC,EF分别交BC、BD于点F、G.
(1)求证:BE=CF;
(2)若AE=BE,在不添加任何辅助线的情况下,请直接写出图中所有的直角三角形.
24.扇形是轴对称图形吗?设计一个方案验证自己的猜测.
25.如图,在平面直角坐标系中有一个△ABC,点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
26.已知△ABC在平面直角坐标系中的位置如图所示,
(1)先画出△ABC关于x轴对称的图形△A1B1C1,再画出△A1B1C1关于y轴对称的图形△A2B2C2;
(2)直接写出△A2B2C2各顶点的坐标.
27.如图,在正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,网格中有一个格点△ABC即三角形的顶点都在格点上.
(1)在图中作出△ABC关于直线l对称的△A1B1C1
(要求A与A1,B与B1,C与C1相对应)
(2)△ABC的面积为 .
(3)在直线l上找一点P,使得PA+PC的和最小.
参考答案
1.解:∵DE垂直平分AC,
∴DA=DC,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=36(cm).
故选:D.
2.解:①当腰是3,底边是7时,不满足三角形的三边关系,因此舍去.
②当底边是3,腰长是7时,能构成三角形,则其周长=3+7+7=17.
故选:B.
3.解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故A正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故B正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故D正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故C错误;
故选:C.
4.解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
又∵∠BAE=∠DAC=90°,
∴∠AEB=∠ADC=60°,
∴∠BAD=∠EAC=30°,
∴图中等腰三角形有△ABC,△ABD,△ACE,△ADE,
故选:B.
5.解:因为最小角为60度,则该三角形的最大角不能大于60度,否则不合题意,则可以得到其三个角均为60度,即是一个等边三角形;
其最大角不大于90度,所以是锐角三角形;
等边三角形是特殊的等腰三角形.
所以前三项正确,即正确有三个.
故选:C.
6.解:根据轴对称的性质可知,台球走过的路径为:
∴该球最后将落入的球袋是4号.
故选:D.
7.解:∵直线MN是四边形AMBN的对称轴,
∴点A与点B对应,
∴AM=BM,AN=BN,∠ANM=∠BNM,
∵点P是直线MN上的点,
∴∠MAP=∠MBP,
∴A,B,C正确,而D错误,
故选:D.
8.解:观察图案可知:
具有轴对称性质的图案只有2个,
第二个需要图2上下翻折可得,
第1个需要左右翻折可得.
故选:C.
9.解:∵∠A=90°,
∴DA⊥BA,
又∵BD是∠ABC的平分线,DE⊥BC,
∴DE=AD,
∵AD=3,
∴DE=3,
故答案为:3.
10.解:∵DE是AC的垂直平分线,
∴DA=DC,AE=EC=5cm,
又∵△ABD的周长为17cm,即AB+BD+AD=17cm,
∴AB+BD+DC=17cm,
∴AB+BC+AC=17+10=27(cm),
即△ABC的周长为27cm.
故答案为:27cm.
11.解:
当110°外角为底角的外角时,则其底角为:180°﹣110°=70°;
当110°外角为顶角的外角时,则其顶角为:70°,则其底角为:=55°,
故答案为:70°或55°.
12.解:如图,在数轴上取点B1,B2,B3,B4,
使OB1=OA=2,OB3=OA=2,AB4=OA=2,
根据题意可知:
OA=2,∠AOB2=45°,
作AB2⊥x轴于点B2,
则OB2=AB2=,
∴OB4=2,
∴数轴上点B所表示的数是:﹣2,,2,2.
故答案为:﹣2或或2或2.
13.解:∵要使所画三角形的一边与BC重合,
∴应顺时针方向再作5个三角形,
∴其边长为1×()5=.
∴这个三角形的边长为.
故填.
14.解:∵DE的垂直平分线分别交AC、BC于点F、G,
∴FE=FD,
∴△DEF为等腰三角形,故①正确;
∵DE⊥AB,DE⊥FG,
∴AB∥FG,
∴∠FGC=∠B=60°,
又∵△ABC是等边三角形,
∴∠C=60°,
∴△CFG中,∠C=∠CFG=∠CGF,
∴△CFG是等边三角形,故②正确;
∵∠FDC>∠FGC=60°,∠C=60°,∠CFD<∠CFG=60°,
∴△CDF不可能是等腰三角形,故③错误;
故答案为:①②.
15.解:如图所示,与△ABC成轴对称且也以格点为顶点的三角形有3个:
故答案为:3.
16.解:如图,
这个单词所指的物品是书.
故答案为:书.
17.解:分别作点P关于OB、AO的对称点P′、P″
分别连OP′、OP″、P′P″交OB、OA于M、N
由轴对称△PMN周长等于PN+NM+MP=P′N+NM+MP″=P′P″
∴由两点之间线段最短可知,此时△PMN周长的最小
∴P′P″=5
由对称OP=OP′=OP″=5
∴△P′OP″为等边三角形
∴∠P′OP″=60°
∵∠P′OB=∠POB,∠P″OA=∠POA
∴∠AOB=∠P′OP″=30°.
故答案为:30°.
18.解:由折叠可得,∠AEF=∠AEA',∠BEG=∠BEB',
∵∠A'EB′=50°,
∴∠AEA'+∠BEB'=130°,
∴∠AEF+∠BEG=(∠AEA'+∠BEB')=130°=65°,
故答案为:65.
19.解:∵AB的中垂线DE交AC于F,
∴AF=BF.
又∵AC=6,BC=4,
∴△BCF的周长=BC+CF+FB=BC+CF+FA=BC+AC=10.
20.解:∵DE是AC的垂直平分线,
∴CD=AD,
∴AB=BD+AD=BD+CD,
设CD=x,则BD=4﹣x,
在Rt△BCD中,
CD2=BC2+BD2,即x2=32+(4﹣x)2,
解得x=.
所以CD的长为:.
21.解:设一边为xcm,则另一边为2xcm,
当长为xcm的边为腰时,此时三角形的三边长分别为xcm、xcm、2xcm,
由题意可列方程:x+x+2x=30,解得x=7.5,此时三角形的三边长分别为:7.5、7.5和15,因为7.5+7.5=15,不符合三角形三边之间的关系,所以不符合题意;
当长为xcm的边为底时,此时三角形的三边长分别为xcm、2xcm、2xcm,
由题意可列方程:x+2x+2x=30,解得x=6,此时三角形的三边长分别为:6、12、12,满足三角形的三边之间的关系,
所以这个三角形的各边长分别为6cm、12cm和12cm.
22.解:①原三角形是锐角三角形,最大角是72°的情况:
如图∠ABC=∠ACB=72°,∠A=36°,AD=BD=BC,则最大角是72°;
,
②原三角形是直角三角形,最大角是90°的情况:
如图∠ABC=90°,∠A=36°,AD=CD=BD,;
③原三角形是钝角三角形,最大角是108°的情况:
如图∠BAC=108°,∠B=36°,BD=AB,AD=DC,
④原三角形是钝角三角形,最大角是126°的情况:
如图∠ABC=126°,∠C=36°,AD=BD=BC,
⑤原三角形是钝角三角形,最大角是132°的情况:
如图∠C=132°,∠ABC=36°,AD=BD,CD=CB,
故答案为:72°,90°,108°,132°,126°.
23.解:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC,
∵DE∥BC,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴BE=DE,
∵DE∥BC,EF∥AC,
∴四边形EFCD是平行四边形,
∴DE=CF,
∴BE=CF.
(2)若AE=BE,则AE=DE=BE,
∴∠A=∠ADE,∠EBD=∠EDB,
又∵∠A+∠ADE+∠EDB+∠EBD=180°,
∴∠ADE+∠EDB=90°,即BD⊥AC,
又∵EF∥AC,
∴BD⊥EF,
∴图中的直角三角形为:△ABD,△CBD,△BEG,△BFG,△DEG.
24.解:根据题意,扇形是轴对称图形,它有1条对称轴.
设计方案如下:
如图,将扇形沿圆心角的角平分线所在直线折叠,两边重合,所以扇形是轴对称图形.
25.解:(1)如图所示;
(2)S△ABC=4×5﹣×2×4﹣×3×3﹣×1×5
=20﹣4﹣﹣
=9.
故答案为:9.
26.解:(1)如图所示,△A1B1C1,△A2B2C2即为所求;
(2)如图所示,A2(﹣5,﹣5),B2(﹣2,﹣3),C2(﹣4,﹣2).
27.解:(1)如图所示:△A1B1C1即为所求;
(2)△ABC的面积为:3×4﹣×2×3+×2×2﹣×1×4=5;
故答案为:5;
(3)如图所示:点P即为所求的点.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
