2020-2021学年七年级数学华东师大版下册第9章《多边形》单元练习题(word版,含答案)
文档属性
| 名称 | 2020-2021学年七年级数学华东师大版下册第9章《多边形》单元练习题(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 12:37:29 | ||
图片预览



文档简介
2021年华师大版七年级下册第9章《多边形》单元必刷题
一.选择题
1.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
2.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长为( )
A.3cm B.4cm C.9cm D.10cm
3.下列说法中错误的是( )
A.三角形的一个外角大于任何一个内角
B.任意三角形的内角和都是180°
C.三角形的中线、角平分线、高线都是线段
D.三角形按角分可分为锐角三角形和直角三角形和钝角三角形
4.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
5.如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
A.15° B.25° C.30° D.10°
6.在△ABC中,若AB=2,AC=4,则BC的长可能是( )
A.2 B.4 C.6 D.8
7.下列图形中具有稳定性的是( )
A.等腰三角形 B.长方形 C.正方形 D.平行四边形
8.如果正n边形的一个外角是40°,则n的值为( )
A.5 B.6 C.8 D.9
9.如图,已知△ABC中,∠A=75°,则∠1+∠2=( )
A.335° B.255° C.155° D.150°
10.已知线段a、b、c分别为三角形的三边长,则化简|a+c﹣b|﹣|c﹣a﹣b|的结果为( )
A.2c﹣2b B.2b﹣2c C.﹣2a D.2a
11.一个等腰三角形的两边长分别为2和5,则它的周长为( )
A.7 B.9 C.12 D.9或12
12.下列几组数中,能作为直角三角形三边长的是( )
A.2,4,5 B.3,4,5 C.4,4,5 D.5,4,5
二.填空题
13.在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于点P,若∠A=50°,则∠BPC的度数是 度.
14.用三个正多边形镶嵌,已知其中两个的边数均为5,则第三个正多边形的边数为 .
15.如果一个正多边形的每个外角都等于72°,那么它是正 边形.
三.解答题
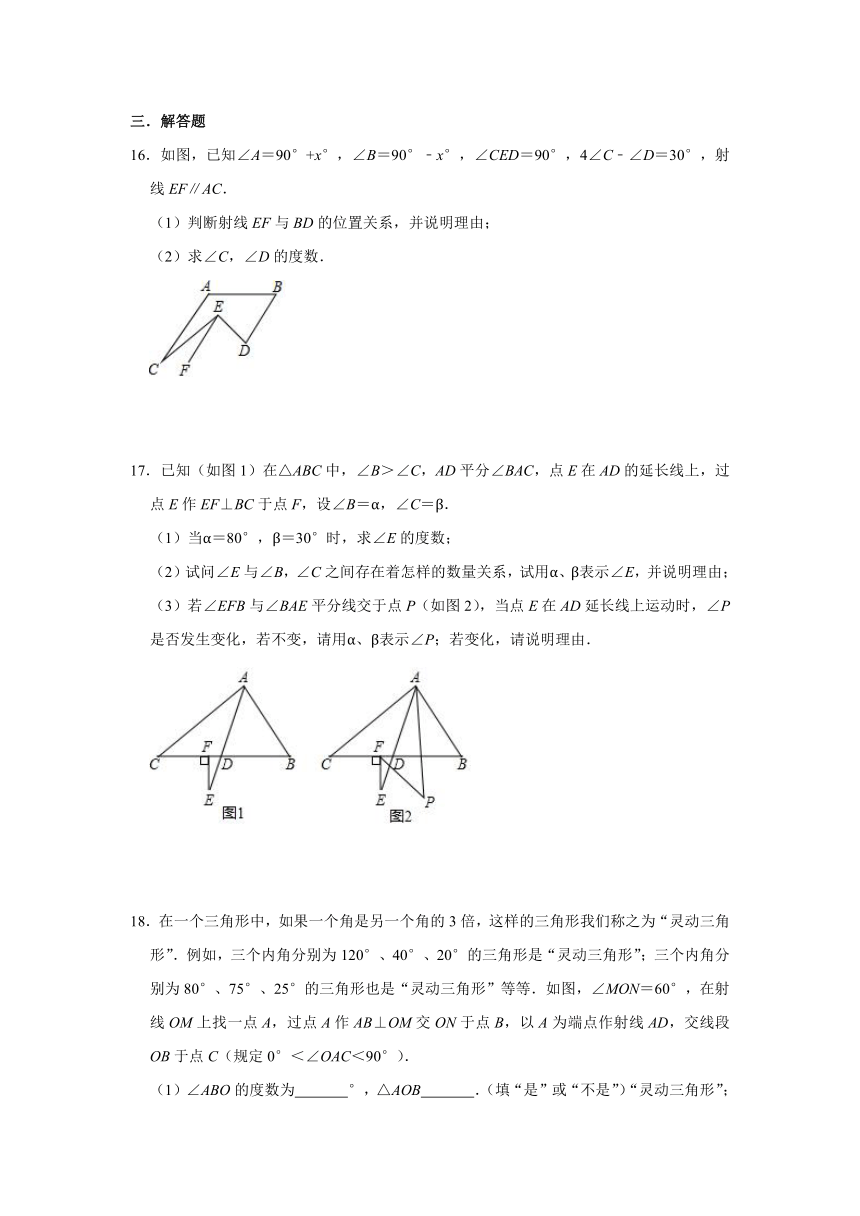
16.如图,已知∠A=90°+x°,∠B=90°﹣x°,∠CED=90°,4∠C﹣∠D=30°,射线EF∥AC.
(1)判断射线EF与BD的位置关系,并说明理由;
(2)求∠C,∠D的度数.
17.已知(如图1)在△ABC中,∠B>∠C,AD平分∠BAC,点E在AD的延长线上,过点E作EF⊥BC于点F,设∠B=α,∠C=β.
(1)当α=80°,β=30°时,求∠E的度数;
(2)试问∠E与∠B,∠C之间存在着怎样的数量关系,试用α、β表示∠E,并说明理由;
(3)若∠EFB与∠BAE平分线交于点P(如图2),当点E在AD延长线上运动时,∠P是否发生变化,若不变,请用α、β表示∠P;若变化,请说明理由.
18.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为 °,△AOB .(填“是”或“不是”)“灵动三角形”;
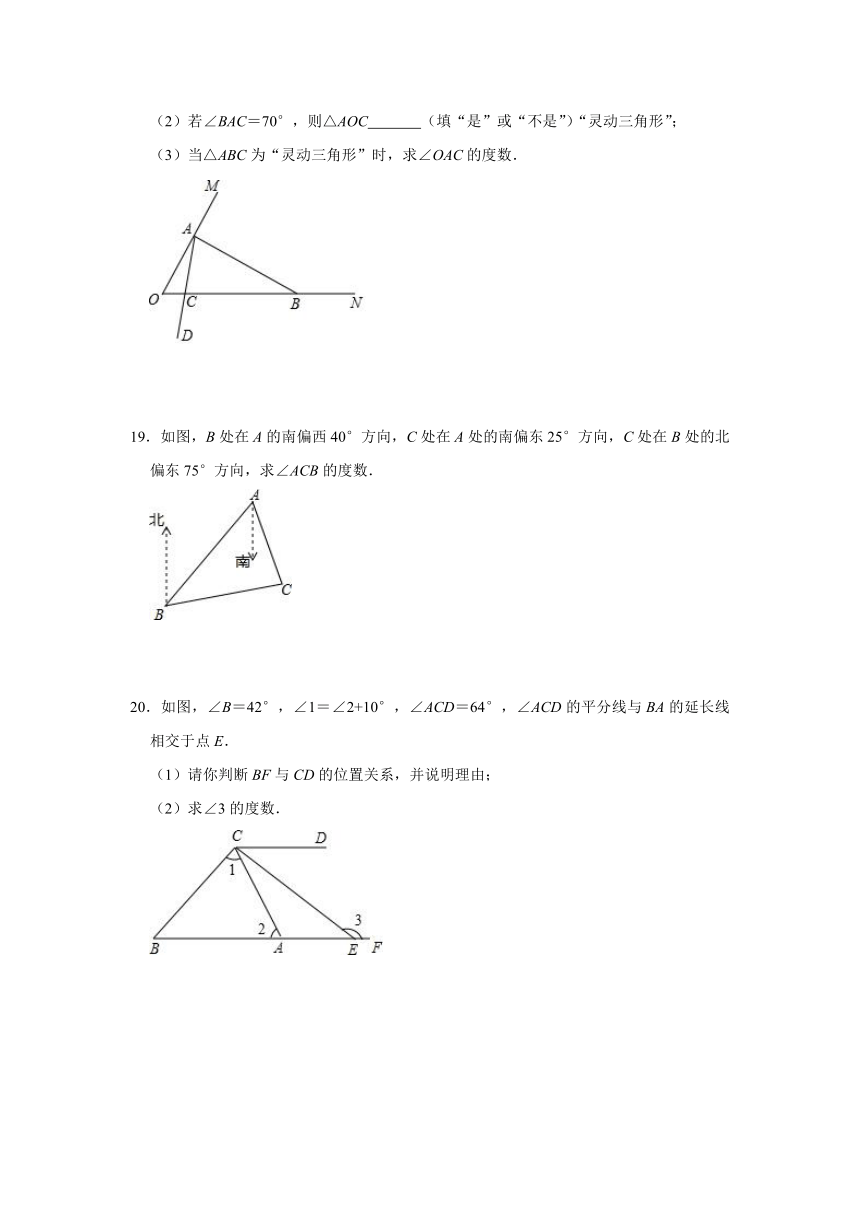
(2)若∠BAC=70°,则△AOC (填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
19.如图,B处在A的南偏西40°方向,C处在A处的南偏东25°方向,C处在B处的北偏东75°方向,求∠ACB的度数.
20.如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.
(1)请你判断BF与CD的位置关系,并说明理由;
(2)求∠3的度数.
21.如图,已知∠1=∠2,∠3=∠4,∠A=100°,求x的值.
22.已知:如图,点D是直线AB上一动点,连接CD.
(1)如图1,当点D在线段AB上时,若∠ABC=105°,∠BCD=30°,求∠ADC度数;
(2)当点D在直线AB上时,请写出∠ADC、∠ABC、∠BCD的数量关系,并证明.
23.已知,如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E的度数.
24.(1)如图1的图形我们把它称为“8字形”,请说明:∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题:
(①)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(②)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
(③)如图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
参考答案
一.选择题
1.解:∵BE为△ABC的高,
∴∠AEB=90°
∵∠C=70°,∠ABC=48°,
∴∠CAB=62°,
∵AF是角平分线,
∴∠1=∠CAB=31°,
在△AEF中,∠EFA=180°﹣31°﹣90°=59°.
∴∠3=∠EFA=59°,
故选:A.
2.解:7﹣3=4,7+3=10,因而4<第三根木棒<10,只有C中的7满足.
故选:C.
3.解:A中当三角形是直角三角形时,有可能外角等于一内角,所以A不正确;
B中任意三角形的内角和都是180°,正确;
C中三角形的中线、角平分线、高线都是线段,正确;
D中三角形按角分可分为锐角三角形和直角三角形和钝角三角形,是三角形的基本分法,正确.
所以只有A错误.
故选:A.
4.解:∵∠A=60°,∠B=40°,
∴∠ACD=∠A+∠B=100°,
∵CE平分∠ACD,
∴∠ECD=∠ACD=50°,
故选:C.
5.解:∵Rt△CDE中,∠C=90°,∠E=30°,
∴∠BDF=∠C+∠E=90°+30°=120°,
∵△BDF中,∠B=45°,∠BDF=120°,
∴∠BFD=180°﹣45°﹣120°=15°.
故选:A.
6.解:∵在△ABC中,若AB=2,AC=4,
∴4﹣2<BC<4+2,
∴2<BC<6,
故选:B.
7.解:等腰三角形,长方形,正方形,平行四边形中只有等腰三角形具有稳定性.
故选:A.
8.解:根据题意得:360°÷40°=9,
则n的值为9,
故选:D.
9.解:∵∠A+∠B+∠C=180°,∠A=75°,
∴∠B+∠C=180°﹣∠A=105°.
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣105°=255°.
故选:B.
10.解:∵a+c﹣b>0,c﹣a﹣b<0,
∴|a+c﹣b|﹣|c﹣a﹣b|
=(a+c﹣b)﹣(﹣c+a+b)
=a+c﹣b+c﹣a﹣b
=2c﹣2b,
故选:A.
11.解:当腰为5时,周长=5+5+2=12;
当腰长为2时,根据三角形三边关系可知此情况不成立;
根据三角形三边关系可知:等腰三角形的腰长只能为5,这个三角形的周长是12.
故选:C.
12.解:A、22+42≠52,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
B、32+42=52,根据勾股定理的逆定理可知三角形是直角三角形,故符合题意;
C、42+42≠52,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
D、42+52≠52,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
故选:B.
二.填空题
13.解:∵CD,BE分别是AB,AC边上的高,
∴∠BDC=∠AEB=90°
∴∠ABE=90°﹣50°=40°
∴∠BPC=∠ABE+∠BDP=40+90=130°.
故答案为:130°.
14.解:正五方形的一个内角度数为108°,
∴一个顶点处取一个角度数为90+120=210,
∴需要的多边形的一个内角度数为360°﹣108°×2=144°,
∴需要的多边形的一个外角度数为180°﹣144°=36°,
∴第三个正多边形的边数为360÷36=10.
故答案为:10.
15.解:这个正多边形的边数:360°÷72°=5.
故答案为:5
三.解答题
16.解:(1)EF∥BD,
∵∠A+∠B=(90+x)°+(90﹣x)°=180°,
∴AC∥BD,
∵EF∥AC,
∴EF∥BD;
(2)∵AC∥EF∥BD,
∴∠CEF=∠C,∠DEF=∠D,
∵∠CED=90°,
∴∠C+∠D=90°,
联立,
解得.
17.解:(1)∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵AD平分∠BAC,
∴∠BAD=BAC=35°,
∴∠EDF=∠ADB=180°﹣35°﹣80°=65°,
∵EF⊥BC,
∴∠EFD=90°,
∴∠E=90°﹣65°=25°;
(2)∵∠EDF=∠C+∠CAD,∠CAD=∠BAC=(180°﹣α﹣β),
∴∠EDF=∠C+90°﹣α﹣β=90°﹣(α﹣β),
∵∠EFD=90°,
∴∠DEF=(α﹣β);
(3)设AP与BC交于G,
∵AD平分∠BAC,
∴∠BAD=BAC=(180°﹣α﹣β),
∵AP平分∠BAE,
∴∠BAP=BAD=(180°﹣α﹣β),
∴∠PGF=∠AGB=180°﹣∠B﹣∠BAP=180°﹣α﹣(180°﹣α﹣β)=135°﹣α+β,
∵PF平分∠EFB,
∴∠PFB=45°,
∴∠P=180°﹣∠PFB﹣∠PGF=180°﹣45°﹣(135°﹣α+β)=α﹣β,
故∠P不会发生变化.
18.解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①∠ACB=3∠ABC时,∠CAB=60°,∠OAC=30°;
②当∠ABC=3∠CAB时,∠CAB=10°,∠OAC=80°.
③当∠ACB=3∠CAB时,∠CAB=37.5°,可得∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
19.解:∵B处在A处的南偏西40°方向,C处在A处的南偏东25°方向,C处在B处的北偏东75°方向,
∴∠ABC=75°﹣40°=35°,∠BAC=40°+25°=65°,
∴∠ACB=180°﹣35°﹣65°=80°.
∠ACB的度数是80°.
20.解:(1)结论:BF∥CD.理由如下:
在三角形ABC中,∠B+∠1+∠2=180°,
∴42°+∠2+∠2+10°=180°,
∴∠2=64°,
又∵∠ACD=64°,
∴∠2=∠ACD,
∴BF∥CD.
(2)∵∠ACD=64°,CE平分∠ACD,
∴∠DCE=×64°=32°,由(1)知BF∥CD,
∴∠3=180°﹣∠DCE=148°.
21.解:∵∠A=100°,
∴∠ABC+∠ACB=180°﹣∠A=80°,
即∠1+∠2+∠3+∠4=80°,
∵∠1=∠2,∠3=∠4,
∴2∠2+2∠4=80°,
∴∠2+∠4=40°,
∴x=180°﹣(∠2+∠4)
=180°﹣40°
=140°.
22.解:(1)如图1中,
∵∠ADC=∠ABC+∠BCD,∠ABC=105°,∠BCD=30°,
∴∠ADC=135°.
(2)如图1中,当点D在线段AB上时,∠ADC=∠ABC+∠BCD.
如图2中,当点D在线段AB的延长线上时,∠ABC=∠ADC+∠BCD.
如图3中,当点D在线段BA的延长线上时,∠ADC+∠ABC+∠BCD=180°.
23.解:∵AB∥CD,AE平分∠BAC,CE平分∠ACD,
又∠BAC+∠DCA=180°?∠CAE+∠ACE=(∠BAC+∠DCA)=90°,
∠E=180°﹣(∠CAE+∠ACE)=90°,
∴∠E=90°.
24.解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①如图2:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4,
由(1)的结论得:∠P+∠3=∠1+∠B①,
∠P+∠2=∠4+∠D②,
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D,
∵∠ABC=36°,∠ADC=16°,
∴∠P=(∠B+∠D)=26°.
②∠P=26°.
如图3:∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
由(1)的结论得:∠PAD+∠P=∠PCD+∠D①,∠PAB+∠P=∠PCB+∠B②,
∵∠PAB=∠1,∠1=∠2,
∴∠PAB=∠2,
∴∠2+∠P=∠3+∠B③,
①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,
∴∠P=(∠B+∠D )=26°.
③如图4,
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴(180°﹣2∠1)+∠B=(180°﹣2∠4)+∠D,
在四边形APCB中,(180°﹣∠1)+∠P+∠4+∠B=360°,
在四边形APCD中,∠2+∠P+(180°﹣∠3)+∠D=360°,
∴2∠P+∠B+∠D=360°,
∴∠P=180°﹣(∠B+∠D).
一.选择题
1.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
2.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长为( )
A.3cm B.4cm C.9cm D.10cm
3.下列说法中错误的是( )
A.三角形的一个外角大于任何一个内角
B.任意三角形的内角和都是180°
C.三角形的中线、角平分线、高线都是线段
D.三角形按角分可分为锐角三角形和直角三角形和钝角三角形
4.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
5.如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )
A.15° B.25° C.30° D.10°
6.在△ABC中,若AB=2,AC=4,则BC的长可能是( )
A.2 B.4 C.6 D.8
7.下列图形中具有稳定性的是( )
A.等腰三角形 B.长方形 C.正方形 D.平行四边形
8.如果正n边形的一个外角是40°,则n的值为( )
A.5 B.6 C.8 D.9
9.如图,已知△ABC中,∠A=75°,则∠1+∠2=( )
A.335° B.255° C.155° D.150°
10.已知线段a、b、c分别为三角形的三边长,则化简|a+c﹣b|﹣|c﹣a﹣b|的结果为( )
A.2c﹣2b B.2b﹣2c C.﹣2a D.2a
11.一个等腰三角形的两边长分别为2和5,则它的周长为( )
A.7 B.9 C.12 D.9或12
12.下列几组数中,能作为直角三角形三边长的是( )
A.2,4,5 B.3,4,5 C.4,4,5 D.5,4,5
二.填空题
13.在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于点P,若∠A=50°,则∠BPC的度数是 度.
14.用三个正多边形镶嵌,已知其中两个的边数均为5,则第三个正多边形的边数为 .
15.如果一个正多边形的每个外角都等于72°,那么它是正 边形.
三.解答题
16.如图,已知∠A=90°+x°,∠B=90°﹣x°,∠CED=90°,4∠C﹣∠D=30°,射线EF∥AC.
(1)判断射线EF与BD的位置关系,并说明理由;
(2)求∠C,∠D的度数.
17.已知(如图1)在△ABC中,∠B>∠C,AD平分∠BAC,点E在AD的延长线上,过点E作EF⊥BC于点F,设∠B=α,∠C=β.
(1)当α=80°,β=30°时,求∠E的度数;
(2)试问∠E与∠B,∠C之间存在着怎样的数量关系,试用α、β表示∠E,并说明理由;
(3)若∠EFB与∠BAE平分线交于点P(如图2),当点E在AD延长线上运动时,∠P是否发生变化,若不变,请用α、β表示∠P;若变化,请说明理由.
18.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为 °,△AOB .(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC (填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
19.如图,B处在A的南偏西40°方向,C处在A处的南偏东25°方向,C处在B处的北偏东75°方向,求∠ACB的度数.
20.如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.
(1)请你判断BF与CD的位置关系,并说明理由;
(2)求∠3的度数.
21.如图,已知∠1=∠2,∠3=∠4,∠A=100°,求x的值.
22.已知:如图,点D是直线AB上一动点,连接CD.
(1)如图1,当点D在线段AB上时,若∠ABC=105°,∠BCD=30°,求∠ADC度数;
(2)当点D在直线AB上时,请写出∠ADC、∠ABC、∠BCD的数量关系,并证明.
23.已知,如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E的度数.
24.(1)如图1的图形我们把它称为“8字形”,请说明:∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题:
(①)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
(②)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
(③)如图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
参考答案
一.选择题
1.解:∵BE为△ABC的高,
∴∠AEB=90°
∵∠C=70°,∠ABC=48°,
∴∠CAB=62°,
∵AF是角平分线,
∴∠1=∠CAB=31°,
在△AEF中,∠EFA=180°﹣31°﹣90°=59°.
∴∠3=∠EFA=59°,
故选:A.
2.解:7﹣3=4,7+3=10,因而4<第三根木棒<10,只有C中的7满足.
故选:C.
3.解:A中当三角形是直角三角形时,有可能外角等于一内角,所以A不正确;
B中任意三角形的内角和都是180°,正确;
C中三角形的中线、角平分线、高线都是线段,正确;
D中三角形按角分可分为锐角三角形和直角三角形和钝角三角形,是三角形的基本分法,正确.
所以只有A错误.
故选:A.
4.解:∵∠A=60°,∠B=40°,
∴∠ACD=∠A+∠B=100°,
∵CE平分∠ACD,
∴∠ECD=∠ACD=50°,
故选:C.
5.解:∵Rt△CDE中,∠C=90°,∠E=30°,
∴∠BDF=∠C+∠E=90°+30°=120°,
∵△BDF中,∠B=45°,∠BDF=120°,
∴∠BFD=180°﹣45°﹣120°=15°.
故选:A.
6.解:∵在△ABC中,若AB=2,AC=4,
∴4﹣2<BC<4+2,
∴2<BC<6,
故选:B.
7.解:等腰三角形,长方形,正方形,平行四边形中只有等腰三角形具有稳定性.
故选:A.
8.解:根据题意得:360°÷40°=9,
则n的值为9,
故选:D.
9.解:∵∠A+∠B+∠C=180°,∠A=75°,
∴∠B+∠C=180°﹣∠A=105°.
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣105°=255°.
故选:B.
10.解:∵a+c﹣b>0,c﹣a﹣b<0,
∴|a+c﹣b|﹣|c﹣a﹣b|
=(a+c﹣b)﹣(﹣c+a+b)
=a+c﹣b+c﹣a﹣b
=2c﹣2b,
故选:A.
11.解:当腰为5时,周长=5+5+2=12;
当腰长为2时,根据三角形三边关系可知此情况不成立;
根据三角形三边关系可知:等腰三角形的腰长只能为5,这个三角形的周长是12.
故选:C.
12.解:A、22+42≠52,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
B、32+42=52,根据勾股定理的逆定理可知三角形是直角三角形,故符合题意;
C、42+42≠52,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
D、42+52≠52,根据勾股定理的逆定理可知三角形不是直角三角形,故不合题意;
故选:B.
二.填空题
13.解:∵CD,BE分别是AB,AC边上的高,
∴∠BDC=∠AEB=90°
∴∠ABE=90°﹣50°=40°
∴∠BPC=∠ABE+∠BDP=40+90=130°.
故答案为:130°.
14.解:正五方形的一个内角度数为108°,
∴一个顶点处取一个角度数为90+120=210,
∴需要的多边形的一个内角度数为360°﹣108°×2=144°,
∴需要的多边形的一个外角度数为180°﹣144°=36°,
∴第三个正多边形的边数为360÷36=10.
故答案为:10.
15.解:这个正多边形的边数:360°÷72°=5.
故答案为:5
三.解答题
16.解:(1)EF∥BD,
∵∠A+∠B=(90+x)°+(90﹣x)°=180°,
∴AC∥BD,
∵EF∥AC,
∴EF∥BD;
(2)∵AC∥EF∥BD,
∴∠CEF=∠C,∠DEF=∠D,
∵∠CED=90°,
∴∠C+∠D=90°,
联立,
解得.
17.解:(1)∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵AD平分∠BAC,
∴∠BAD=BAC=35°,
∴∠EDF=∠ADB=180°﹣35°﹣80°=65°,
∵EF⊥BC,
∴∠EFD=90°,
∴∠E=90°﹣65°=25°;
(2)∵∠EDF=∠C+∠CAD,∠CAD=∠BAC=(180°﹣α﹣β),
∴∠EDF=∠C+90°﹣α﹣β=90°﹣(α﹣β),
∵∠EFD=90°,
∴∠DEF=(α﹣β);
(3)设AP与BC交于G,
∵AD平分∠BAC,
∴∠BAD=BAC=(180°﹣α﹣β),
∵AP平分∠BAE,
∴∠BAP=BAD=(180°﹣α﹣β),
∴∠PGF=∠AGB=180°﹣∠B﹣∠BAP=180°﹣α﹣(180°﹣α﹣β)=135°﹣α+β,
∵PF平分∠EFB,
∴∠PFB=45°,
∴∠P=180°﹣∠PFB﹣∠PGF=180°﹣45°﹣(135°﹣α+β)=α﹣β,
故∠P不会发生变化.
18.解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①∠ACB=3∠ABC时,∠CAB=60°,∠OAC=30°;
②当∠ABC=3∠CAB时,∠CAB=10°,∠OAC=80°.
③当∠ACB=3∠CAB时,∠CAB=37.5°,可得∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
19.解:∵B处在A处的南偏西40°方向,C处在A处的南偏东25°方向,C处在B处的北偏东75°方向,
∴∠ABC=75°﹣40°=35°,∠BAC=40°+25°=65°,
∴∠ACB=180°﹣35°﹣65°=80°.
∠ACB的度数是80°.
20.解:(1)结论:BF∥CD.理由如下:
在三角形ABC中,∠B+∠1+∠2=180°,
∴42°+∠2+∠2+10°=180°,
∴∠2=64°,
又∵∠ACD=64°,
∴∠2=∠ACD,
∴BF∥CD.
(2)∵∠ACD=64°,CE平分∠ACD,
∴∠DCE=×64°=32°,由(1)知BF∥CD,
∴∠3=180°﹣∠DCE=148°.
21.解:∵∠A=100°,
∴∠ABC+∠ACB=180°﹣∠A=80°,
即∠1+∠2+∠3+∠4=80°,
∵∠1=∠2,∠3=∠4,
∴2∠2+2∠4=80°,
∴∠2+∠4=40°,
∴x=180°﹣(∠2+∠4)
=180°﹣40°
=140°.
22.解:(1)如图1中,
∵∠ADC=∠ABC+∠BCD,∠ABC=105°,∠BCD=30°,
∴∠ADC=135°.
(2)如图1中,当点D在线段AB上时,∠ADC=∠ABC+∠BCD.
如图2中,当点D在线段AB的延长线上时,∠ABC=∠ADC+∠BCD.
如图3中,当点D在线段BA的延长线上时,∠ADC+∠ABC+∠BCD=180°.
23.解:∵AB∥CD,AE平分∠BAC,CE平分∠ACD,
又∠BAC+∠DCA=180°?∠CAE+∠ACE=(∠BAC+∠DCA)=90°,
∠E=180°﹣(∠CAE+∠ACE)=90°,
∴∠E=90°.
24.解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①如图2:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4,
由(1)的结论得:∠P+∠3=∠1+∠B①,
∠P+∠2=∠4+∠D②,
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D,
∵∠ABC=36°,∠ADC=16°,
∴∠P=(∠B+∠D)=26°.
②∠P=26°.
如图3:∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
由(1)的结论得:∠PAD+∠P=∠PCD+∠D①,∠PAB+∠P=∠PCB+∠B②,
∵∠PAB=∠1,∠1=∠2,
∴∠PAB=∠2,
∴∠2+∠P=∠3+∠B③,
①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,
∴∠P=(∠B+∠D )=26°.
③如图4,
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴(180°﹣2∠1)+∠B=(180°﹣2∠4)+∠D,
在四边形APCB中,(180°﹣∠1)+∠P+∠4+∠B=360°,
在四边形APCD中,∠2+∠P+(180°﹣∠3)+∠D=360°,
∴2∠P+∠B+∠D=360°,
∴∠P=180°﹣(∠B+∠D).
