(机构适用)第8章成对数据的统计分析总结-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册练习(Word含解析)
文档属性
| 名称 | (机构适用)第8章成对数据的统计分析总结-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册练习(Word含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 447.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 00:00:00 | ||
图片预览




文档简介
第八章总结习题
一、单选题
1.已知变量和的回归直线方程为,变量与负相关.下列结论中正确的是(
)
A.与正相关,与负相关
B.与正相关,与正相关
C.与负相关,与负相关
D.与负相关,与正相关
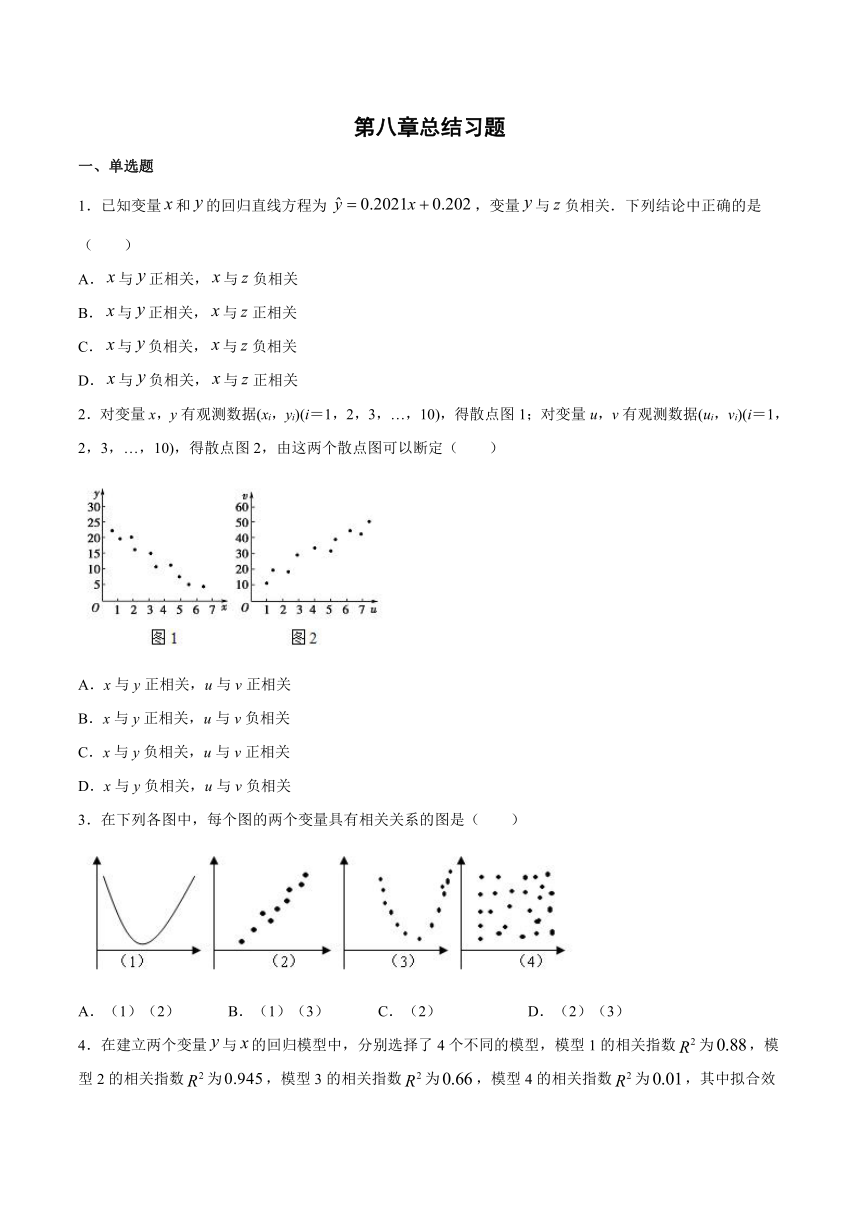
2.对变量x,y有观测数据(xi,yi)(i=1,2,3,…,10),得散点图1;对变量u,v有观测数据(ui,vi)(i=1,2,3,…,10),得散点图2,由这两个散点图可以断定(
)
A.x与y正相关,u与v正相关
B.x与y正相关,u与v负相关
C.x与y负相关,u与v正相关
D.x与y负相关,u与v负相关
3.在下列各图中,每个图的两个变量具有相关关系的图是(
)
A.(1)(2)
B.(1)(3)
C.(2)
D.(2)(3)
4.在建立两个变量与的回归模型中,分别选择了4个不同的模型,模型1的相关指数为,模型2的相关指数为,模型3的相关指数为,模型4的相关指数为,其中拟合效果最好的模型是(
)
A.模型1
B.模型2
C.模型3
D.模型4
5.两个具有线性相关关系的变量的一组数据,,…,下列说法错误的是
A.相关系数越接近1,变量相关性越强
B.落在回归直线方程上的样本点越多,回归直线方程拟合效果越好
C.相关指数越小,残差平方和越大,即模型的拟合效果越差
D.若表示女大学生的身高,表示体重则表示女大学生的身高解释了的体重变化
6.某服装厂引进新技术,其生产服装的产量(百件)与单位成本(元)满足回归直线方程,则以下说法正确的是()
A.产量每增加100件,单位成本约下降元
B.产量每减少100件,单位成本约上升元
C.产量每增加100件,单位成本约上升元
D.产量每减少100件,单位成本约下降元
7.某公司为确定明年投入某产品的广告支出,对近年的广告支出与销售额(单位:百万元)进行了初步统计,得到下列表格中的数据:
经测算,年广告支出与年销售额满足线性回归方程,则的值为(
)
A.
B.
C.
D.
8.已知变量x,y之间具有线性相关关系,其回归方程为=-3+x,若=17,,则的值为( )
A.2
B.1
C.-2
D.-1
9.某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温x(℃)
18
13
10
-1
用电量y(度)
24
34
38
64
由表中数据得线性回归方程=x+中≈-2,预测当气温为-4℃时,用电量的度数约为(
)
A.58
B.66
C.68
D.70
10.如图,根据已知的散点图,得到y关于x的线性回归方程为,则(
)
A.1.5
B.1.8
C.2
D.1.6
11.下列有关统计知识的四个命题正确的是
A.衡量两变量之间线性相关关系的相关系数越接近,说明两变量间线性关系越密切
B.在回归分析中,可以用卡方来刻画回归的效果,越大,模型的拟合效果越差
C.线性回归方程对应的直线至少经过其样本数据点中的一个点
D.线性回归方程中,变量每增加一个单位时,变量平均增加个单位
12.已知变量负相关,且由观测数据算得样本平均数,则由该观测数据得到的线性回归方程可能是
A.
B.
C.
D.
13.假设两个分类变量和,他们的取值分别为和,其样本频数列联表如下:
总计
总计
对于以下数据,对同一样本说明与有关的可能性最大的一组是(
)
A.,,,
B.,,,
C.,,,
D.,,,
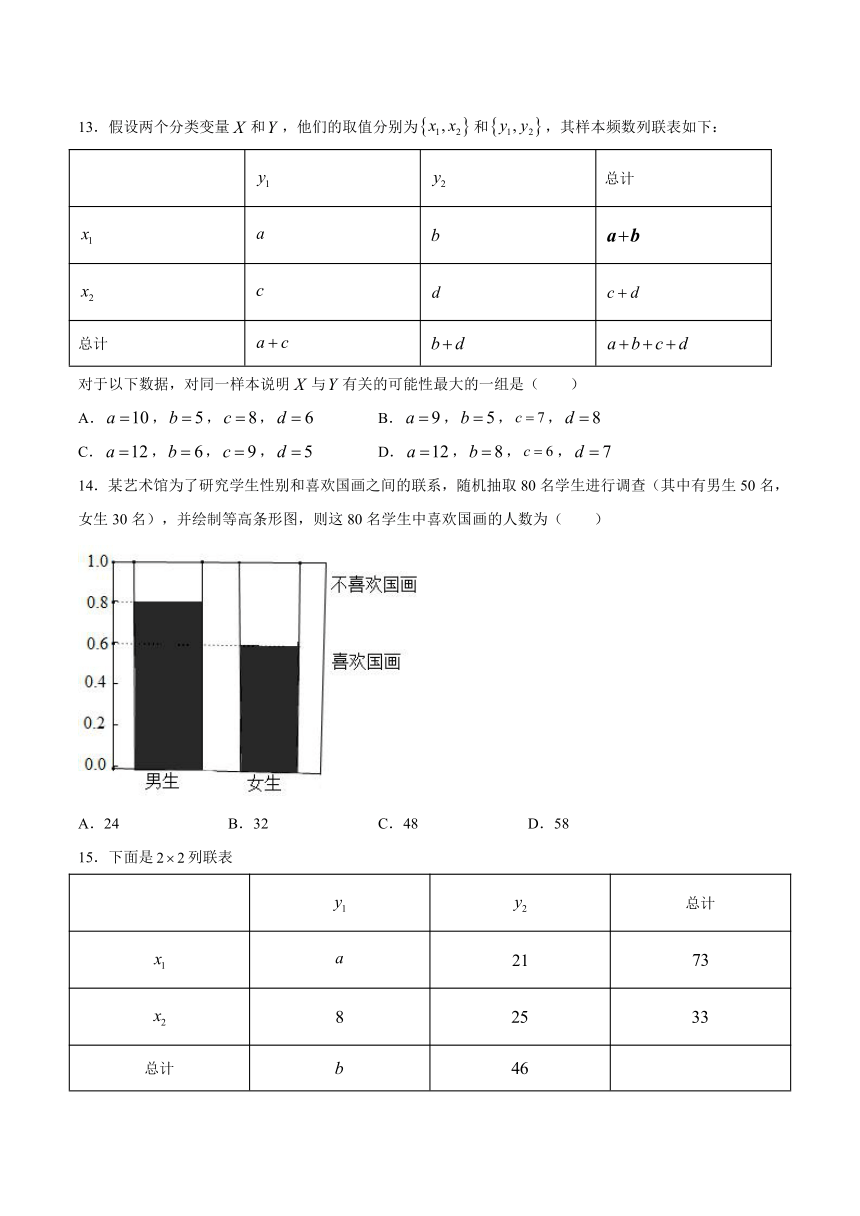
14.某艺术馆为了研究学生性别和喜欢国画之间的联系,随机抽取80名学生进行调查(其中有男生50名,女生30名),并绘制等高条形图,则这80名学生中喜欢国画的人数为(
)
A.24
B.32
C.48
D.58
15.下面是列联表
总计
总计
则表中、处的值为(
)
A.、
B.、
C.、
D.、
16.经过对x2的统计量的研究,得到了若干个临界值,当x2<2.706时,我们认为事件A与B(
)
α
0.1
0.05
0.01
0.005
0.001
xα
2.706
3.841
6.635
7.879
10.828
A.有95%的把握认为A与B有关系
B.有99%的把握认为A与B有关系
C.没有充分理由说明事件A与B有关系
D.不能确定
17.某校为了研究学生的性别和对待某一活动的态度(支持与不支持)的关系,运用列联表进行独立性检验,经计算,则所得到的统计学结论是:有__________的把握认为“学生性别与支持该活动有关系”(
)
0.100
0.050
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828
A.
B.
C.
D.
18.在一个列联表中,由其数据计算得到的观测值,临界值表为:
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.84
5.024
6.635
7.879
10.83
则其两个变量间有关系的可能性为
A.
B.
C.
D.0
第II卷(非选择题)
请点击修改第II卷的文字说明
二、解答题
19.有一种速度叫中国速度,有一种骄傲叫中国高铁.中国高铁经过十几年的发展,取得了举世瞩目的成就,使我国完成了从较落后向先进铁路国的跨越式转变.中国的高铁技术不但越来越成熟,而且还走向国外,帮助不少国家修建了高铁.高铁可以说是中国一张行走的名片.截至到2020年,中国高铁运营里程已经达到3.9万公里.下表是2013年至2020年中国高铁每年的运营里程统计表,它反映了中国高铁近几年的飞速发展:
年份
2013
2014
2015
2016
2017
2018
2019
2020
年份代码
1
2
3
4
5
6
7
8
运营里程万公里
1.3
1.6
1.9
2.2
2.5
2.9
3.5
3.9
根据以上数据,回答下面问题.
(1)甲同学用曲线y=bx+a来拟合,并算得相关系数r1=0.97,乙同学用曲线y=cedx来拟合,并算得转化为线性回归方程所对应的相关系数r2=0.99,试问哪一个更适合作为y关于x的回归方程类型,并说明理由;
(2)根据(1)的判断结果及表中数据,求y关于x的回归方程(系数精确到0.01).
参考公式:用最小二乘法求线性回归方程的系数公式:;参考数据:令
20.近年来上饶市积极开展“创文创卫”活动,深入学习宣传贯彻党的十九届五中全会精神,坚持以人民为中心的发展思想,以深化全国文明城市建设为抓手,让文明的种子在上饶大地继续播撒,浸润于每一位市民的日常行为中,镌刻在上饶城市精神的最深处.广大学生也积极投身文明宣传活动,某班级在活动的前2天大力宣传后,从第3天开始连续统计了4天的参与活动的学生人数如下:
第天
3
4
5
6
人数
17
20
19
24
(1)从以上4天中随机选取2天,求这2天参与活动均在20人以上(含20人)的概率;
(2)根据表中4组数据,求关于的线性回归方程;并预测第10天的参与人数.
参考公式:回归直线中,.
21.随着国内疫情得到有效控制,各商家经营活动逐步恢复正常,部分商家还积极推岀新产品,吸引更多的消费者前来消费.某商店推出了一种新的产品,并选择对某一天来消费这种新产品的顾客共人进行满意度调查,为此相关人员制作了如下的列联表.
满意
不满意
总计
男顾客
女顾客
总计
已知从全部人中随机抽取人为满意的概为.
(1)请完成如上的列联表;
(2)根据列联表的数据,是否能在犯错率不超过的前提下认为“满意度与性别有关系”?
(3)为了进一步改良这种新产品,商家在当天不满意的顾客中,按照性别利用分层抽样抽取了人进行回访,并从这人中再随机抽取人送出奖品,求获奖者性别不全相同的概率.
附注:.
参考答案
1.【答案】A
【分析】
因为直线的斜率大于0,故与正相关,
因为与负相关,可设,,
则,
因为,
故与负相关.
2.【答案】C
【分析】
由图1可知,点散布在从左上角到右下角的区域,各点整体呈递减趋势,故x与y负相关;
由图2可知,点散布在从左下角到右上角的区域,各点整体呈递增趋势,故u与v正相关.
故选:C.
3.【答案】D
【分析】
对(1),所有的点都在曲线上,故具有函数关系;
对(2),所有的散点分布在一条直线附近,具有相关关系;
对(3),所有的散点分布在一条曲线附近,具有相关关系;
对(4),所有的散点杂乱无章,不具有相关关系.
故选:D.
4.【答案】B
【分析】
所给四个模型中,模型2的相关指数最大,回归模型的拟合效果越好.
故选:B.
5.【答案】B
【分析】
解:对于A.
根据相关系数越接近1,变量相关性越强,故正确;
对于B.
回归直线方程拟合效果的强弱是由相关指数或相关系数判定,故不正确;
对于C.
相关指数越小,残差平方和越大,效果越差,故正确;
对于D.
根据的实际意义可得,表示女大学生的身高解释了的体重变化,故正确;
故选:B
6.【答案】A
【分析】
解:表示产量每增加100件,单位成本约下降元,
故选:A
7.【答案】D
【解析】
由题意得,,
所以,解得,故选D.
8.【答案】A
【解析】
依题意知,,,而直线一定经过点,
所以,解得.
9.【答案】C
【解析】
试题分析:由表中数据可知:样本中心点为,在线性回归方程=x+中≈-2所以=60即回归方程为=-2x+60所以由此预测当气温为-4℃时,用电量的度数约为68.
10.【答案】D
【分析】
因为,所以,解得.
故选:D.
11.【答案】A
【分析】
利用“卡方”的意义、相关指数的意义及回归分析的适用范围,逐一分析四个答案的真假,可得答案.
A.
衡量两变量之间线性相关关系的相关系数越接近,说明两变量间线性关系越密切,正确;
B.
在回归分析中,可以用卡方来刻画回归的效果,越大,模型的拟合效果越差,错误
对分类变量与的随机变量的观测值来说,
越大,“与有关系”可信程度越大;
故B错误;
C.
线性回归方程对应的直线至少经过其样本数据点中的一个点,错误,回归直线可能不经过其样本数据点中的任何一个点;
D.
线性回归方程中,变量每增加一个单位时,变量平均增加个单位,错误,由回归方程可知变量每增加一个单位时,变量平均增加个单位.
故选A.
点睛:本题考查回归分析的意义以及注意的问题.是对回归分析的思想、方法小结.要结合实例进行掌握.
12.【答案】D
【分析】
利用变量与负相关,排除选项,,再利用回归直线方程过样本中心点,代入验证即可
详解:根据变量与负相关,排除选项,,
再根据回归直线方程过样本中心代入,
满足,
13.【答案】B
【分析】
一般地,越大,说明与有关的可能性越大.
选项A中,;
选项B中,;
选项C中,;
选项D中,.
14.【答案】D
【分析】
由等高条形图可知,男生中喜欢国画的占,女生中喜欢国画的占
则这80名学生中喜欢国画的人数为
故选:D
15.【答案】B
【分析】
由表格中的数据可得,解得.
故选:B.
16.【答案】C
【分析】
当x2≥2.706时,有90%以上的把握说明A与B有关系,但当x2<2.706时,只能说明A与B是否有关系的理由不够充分
故选:C.
17.【答案】C
【分析】
,
对照表格:,
因此有把握认为“学生性别与支持该活动没有关系”.
有的把握认为“学生性别与是否支持该活动有关系”,
故选:C.
18.【答案】A
【分析】
因为,所以两个变量无关的可能性为,
因此两个变量有关的可能性为.
19.【答案】(1)答案见解析;(2).
【分析】
解:(1)∵,∴更适合作为y关于x的回归方程类型.
(2),由得,
即,则,
,所以.
20.【答案】(1);(2);预测第10天的参与人数为31人.
【分析】
解:(1)由表格可以得到,从4天中随机取2天,共有种选法,
而第4天和第6天参与活动的人数均在20人以上(含20人),参与活动均在20人以上(含20人)的共有2天,只有1种选法,
故这2天参与活动均在20人以上(含20人)的概率为;
(2)根据表中的数据可得,,,所以,
故,
所以回归直线为,
当时,参与人数人,即预测第10天的参与人数为31人.
21.【答案】(1)列联表见解析;(2)能;(3).
【分析】
(1)根据题意设女顾客满意的有人,结合列联表知,解得.
于是可完成列联表如下:
满意
不满意
总计
男顾客
女顾客
总计
(2)根据列联表中的数据可以得到的观测值,
即,
由此可以判断能在犯错率不超过的前提下认为满意度与性别有关系.
(3)不满意的男性人,女性人,共人,
因此抽取的人中,男性为人,女性为人,
从人中任取人的情况有种
其中人性别相同的情况有种,
所以,
人性别不全相同的概率为.
一、单选题
1.已知变量和的回归直线方程为,变量与负相关.下列结论中正确的是(
)
A.与正相关,与负相关
B.与正相关,与正相关
C.与负相关,与负相关
D.与负相关,与正相关
2.对变量x,y有观测数据(xi,yi)(i=1,2,3,…,10),得散点图1;对变量u,v有观测数据(ui,vi)(i=1,2,3,…,10),得散点图2,由这两个散点图可以断定(
)
A.x与y正相关,u与v正相关
B.x与y正相关,u与v负相关
C.x与y负相关,u与v正相关
D.x与y负相关,u与v负相关
3.在下列各图中,每个图的两个变量具有相关关系的图是(
)
A.(1)(2)
B.(1)(3)
C.(2)
D.(2)(3)
4.在建立两个变量与的回归模型中,分别选择了4个不同的模型,模型1的相关指数为,模型2的相关指数为,模型3的相关指数为,模型4的相关指数为,其中拟合效果最好的模型是(
)
A.模型1
B.模型2
C.模型3
D.模型4
5.两个具有线性相关关系的变量的一组数据,,…,下列说法错误的是
A.相关系数越接近1,变量相关性越强
B.落在回归直线方程上的样本点越多,回归直线方程拟合效果越好
C.相关指数越小,残差平方和越大,即模型的拟合效果越差
D.若表示女大学生的身高,表示体重则表示女大学生的身高解释了的体重变化
6.某服装厂引进新技术,其生产服装的产量(百件)与单位成本(元)满足回归直线方程,则以下说法正确的是()
A.产量每增加100件,单位成本约下降元
B.产量每减少100件,单位成本约上升元
C.产量每增加100件,单位成本约上升元
D.产量每减少100件,单位成本约下降元
7.某公司为确定明年投入某产品的广告支出,对近年的广告支出与销售额(单位:百万元)进行了初步统计,得到下列表格中的数据:
经测算,年广告支出与年销售额满足线性回归方程,则的值为(
)
A.
B.
C.
D.
8.已知变量x,y之间具有线性相关关系,其回归方程为=-3+x,若=17,,则的值为( )
A.2
B.1
C.-2
D.-1
9.某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
气温x(℃)
18
13
10
-1
用电量y(度)
24
34
38
64
由表中数据得线性回归方程=x+中≈-2,预测当气温为-4℃时,用电量的度数约为(
)
A.58
B.66
C.68
D.70
10.如图,根据已知的散点图,得到y关于x的线性回归方程为,则(
)
A.1.5
B.1.8
C.2
D.1.6
11.下列有关统计知识的四个命题正确的是
A.衡量两变量之间线性相关关系的相关系数越接近,说明两变量间线性关系越密切
B.在回归分析中,可以用卡方来刻画回归的效果,越大,模型的拟合效果越差
C.线性回归方程对应的直线至少经过其样本数据点中的一个点
D.线性回归方程中,变量每增加一个单位时,变量平均增加个单位
12.已知变量负相关,且由观测数据算得样本平均数,则由该观测数据得到的线性回归方程可能是
A.
B.
C.
D.
13.假设两个分类变量和,他们的取值分别为和,其样本频数列联表如下:
总计
总计
对于以下数据,对同一样本说明与有关的可能性最大的一组是(
)
A.,,,
B.,,,
C.,,,
D.,,,
14.某艺术馆为了研究学生性别和喜欢国画之间的联系,随机抽取80名学生进行调查(其中有男生50名,女生30名),并绘制等高条形图,则这80名学生中喜欢国画的人数为(
)
A.24
B.32
C.48
D.58
15.下面是列联表
总计
总计
则表中、处的值为(
)
A.、
B.、
C.、
D.、
16.经过对x2的统计量的研究,得到了若干个临界值,当x2<2.706时,我们认为事件A与B(
)
α
0.1
0.05
0.01
0.005
0.001
xα
2.706
3.841
6.635
7.879
10.828
A.有95%的把握认为A与B有关系
B.有99%的把握认为A与B有关系
C.没有充分理由说明事件A与B有关系
D.不能确定
17.某校为了研究学生的性别和对待某一活动的态度(支持与不支持)的关系,运用列联表进行独立性检验,经计算,则所得到的统计学结论是:有__________的把握认为“学生性别与支持该活动有关系”(
)
0.100
0.050
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828
A.
B.
C.
D.
18.在一个列联表中,由其数据计算得到的观测值,临界值表为:
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
0.455
0.708
1.323
2.072
2.706
3.84
5.024
6.635
7.879
10.83
则其两个变量间有关系的可能性为
A.
B.
C.
D.0
第II卷(非选择题)
请点击修改第II卷的文字说明
二、解答题
19.有一种速度叫中国速度,有一种骄傲叫中国高铁.中国高铁经过十几年的发展,取得了举世瞩目的成就,使我国完成了从较落后向先进铁路国的跨越式转变.中国的高铁技术不但越来越成熟,而且还走向国外,帮助不少国家修建了高铁.高铁可以说是中国一张行走的名片.截至到2020年,中国高铁运营里程已经达到3.9万公里.下表是2013年至2020年中国高铁每年的运营里程统计表,它反映了中国高铁近几年的飞速发展:
年份
2013
2014
2015
2016
2017
2018
2019
2020
年份代码
1
2
3
4
5
6
7
8
运营里程万公里
1.3
1.6
1.9
2.2
2.5
2.9
3.5
3.9
根据以上数据,回答下面问题.
(1)甲同学用曲线y=bx+a来拟合,并算得相关系数r1=0.97,乙同学用曲线y=cedx来拟合,并算得转化为线性回归方程所对应的相关系数r2=0.99,试问哪一个更适合作为y关于x的回归方程类型,并说明理由;
(2)根据(1)的判断结果及表中数据,求y关于x的回归方程(系数精确到0.01).
参考公式:用最小二乘法求线性回归方程的系数公式:;参考数据:令
20.近年来上饶市积极开展“创文创卫”活动,深入学习宣传贯彻党的十九届五中全会精神,坚持以人民为中心的发展思想,以深化全国文明城市建设为抓手,让文明的种子在上饶大地继续播撒,浸润于每一位市民的日常行为中,镌刻在上饶城市精神的最深处.广大学生也积极投身文明宣传活动,某班级在活动的前2天大力宣传后,从第3天开始连续统计了4天的参与活动的学生人数如下:
第天
3
4
5
6
人数
17
20
19
24
(1)从以上4天中随机选取2天,求这2天参与活动均在20人以上(含20人)的概率;
(2)根据表中4组数据,求关于的线性回归方程;并预测第10天的参与人数.
参考公式:回归直线中,.
21.随着国内疫情得到有效控制,各商家经营活动逐步恢复正常,部分商家还积极推岀新产品,吸引更多的消费者前来消费.某商店推出了一种新的产品,并选择对某一天来消费这种新产品的顾客共人进行满意度调查,为此相关人员制作了如下的列联表.
满意
不满意
总计
男顾客
女顾客
总计
已知从全部人中随机抽取人为满意的概为.
(1)请完成如上的列联表;
(2)根据列联表的数据,是否能在犯错率不超过的前提下认为“满意度与性别有关系”?
(3)为了进一步改良这种新产品,商家在当天不满意的顾客中,按照性别利用分层抽样抽取了人进行回访,并从这人中再随机抽取人送出奖品,求获奖者性别不全相同的概率.
附注:.
参考答案
1.【答案】A
【分析】
因为直线的斜率大于0,故与正相关,
因为与负相关,可设,,
则,
因为,
故与负相关.
2.【答案】C
【分析】
由图1可知,点散布在从左上角到右下角的区域,各点整体呈递减趋势,故x与y负相关;
由图2可知,点散布在从左下角到右上角的区域,各点整体呈递增趋势,故u与v正相关.
故选:C.
3.【答案】D
【分析】
对(1),所有的点都在曲线上,故具有函数关系;
对(2),所有的散点分布在一条直线附近,具有相关关系;
对(3),所有的散点分布在一条曲线附近,具有相关关系;
对(4),所有的散点杂乱无章,不具有相关关系.
故选:D.
4.【答案】B
【分析】
所给四个模型中,模型2的相关指数最大,回归模型的拟合效果越好.
故选:B.
5.【答案】B
【分析】
解:对于A.
根据相关系数越接近1,变量相关性越强,故正确;
对于B.
回归直线方程拟合效果的强弱是由相关指数或相关系数判定,故不正确;
对于C.
相关指数越小,残差平方和越大,效果越差,故正确;
对于D.
根据的实际意义可得,表示女大学生的身高解释了的体重变化,故正确;
故选:B
6.【答案】A
【分析】
解:表示产量每增加100件,单位成本约下降元,
故选:A
7.【答案】D
【解析】
由题意得,,
所以,解得,故选D.
8.【答案】A
【解析】
依题意知,,,而直线一定经过点,
所以,解得.
9.【答案】C
【解析】
试题分析:由表中数据可知:样本中心点为,在线性回归方程=x+中≈-2所以=60即回归方程为=-2x+60所以由此预测当气温为-4℃时,用电量的度数约为68.
10.【答案】D
【分析】
因为,所以,解得.
故选:D.
11.【答案】A
【分析】
利用“卡方”的意义、相关指数的意义及回归分析的适用范围,逐一分析四个答案的真假,可得答案.
A.
衡量两变量之间线性相关关系的相关系数越接近,说明两变量间线性关系越密切,正确;
B.
在回归分析中,可以用卡方来刻画回归的效果,越大,模型的拟合效果越差,错误
对分类变量与的随机变量的观测值来说,
越大,“与有关系”可信程度越大;
故B错误;
C.
线性回归方程对应的直线至少经过其样本数据点中的一个点,错误,回归直线可能不经过其样本数据点中的任何一个点;
D.
线性回归方程中,变量每增加一个单位时,变量平均增加个单位,错误,由回归方程可知变量每增加一个单位时,变量平均增加个单位.
故选A.
点睛:本题考查回归分析的意义以及注意的问题.是对回归分析的思想、方法小结.要结合实例进行掌握.
12.【答案】D
【分析】
利用变量与负相关,排除选项,,再利用回归直线方程过样本中心点,代入验证即可
详解:根据变量与负相关,排除选项,,
再根据回归直线方程过样本中心代入,
满足,
13.【答案】B
【分析】
一般地,越大,说明与有关的可能性越大.
选项A中,;
选项B中,;
选项C中,;
选项D中,.
14.【答案】D
【分析】
由等高条形图可知,男生中喜欢国画的占,女生中喜欢国画的占
则这80名学生中喜欢国画的人数为
故选:D
15.【答案】B
【分析】
由表格中的数据可得,解得.
故选:B.
16.【答案】C
【分析】
当x2≥2.706时,有90%以上的把握说明A与B有关系,但当x2<2.706时,只能说明A与B是否有关系的理由不够充分
故选:C.
17.【答案】C
【分析】
,
对照表格:,
因此有把握认为“学生性别与支持该活动没有关系”.
有的把握认为“学生性别与是否支持该活动有关系”,
故选:C.
18.【答案】A
【分析】
因为,所以两个变量无关的可能性为,
因此两个变量有关的可能性为.
19.【答案】(1)答案见解析;(2).
【分析】
解:(1)∵,∴更适合作为y关于x的回归方程类型.
(2),由得,
即,则,
,所以.
20.【答案】(1);(2);预测第10天的参与人数为31人.
【分析】
解:(1)由表格可以得到,从4天中随机取2天,共有种选法,
而第4天和第6天参与活动的人数均在20人以上(含20人),参与活动均在20人以上(含20人)的共有2天,只有1种选法,
故这2天参与活动均在20人以上(含20人)的概率为;
(2)根据表中的数据可得,,,所以,
故,
所以回归直线为,
当时,参与人数人,即预测第10天的参与人数为31人.
21.【答案】(1)列联表见解析;(2)能;(3).
【分析】
(1)根据题意设女顾客满意的有人,结合列联表知,解得.
于是可完成列联表如下:
满意
不满意
总计
男顾客
女顾客
总计
(2)根据列联表中的数据可以得到的观测值,
即,
由此可以判断能在犯错率不超过的前提下认为满意度与性别有关系.
(3)不满意的男性人,女性人,共人,
因此抽取的人中,男性为人,女性为人,
从人中任取人的情况有种
其中人性别相同的情况有种,
所以,
人性别不全相同的概率为.
