9.3统计案例公司员工肥胖情况调查分析-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案)
文档属性
| 名称 | 9.3统计案例公司员工肥胖情况调查分析-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习(Word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 267.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 11:25:22 | ||
图片预览



文档简介
本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
9.3统计案例公司员工肥胖情况调查分析
一、单选题
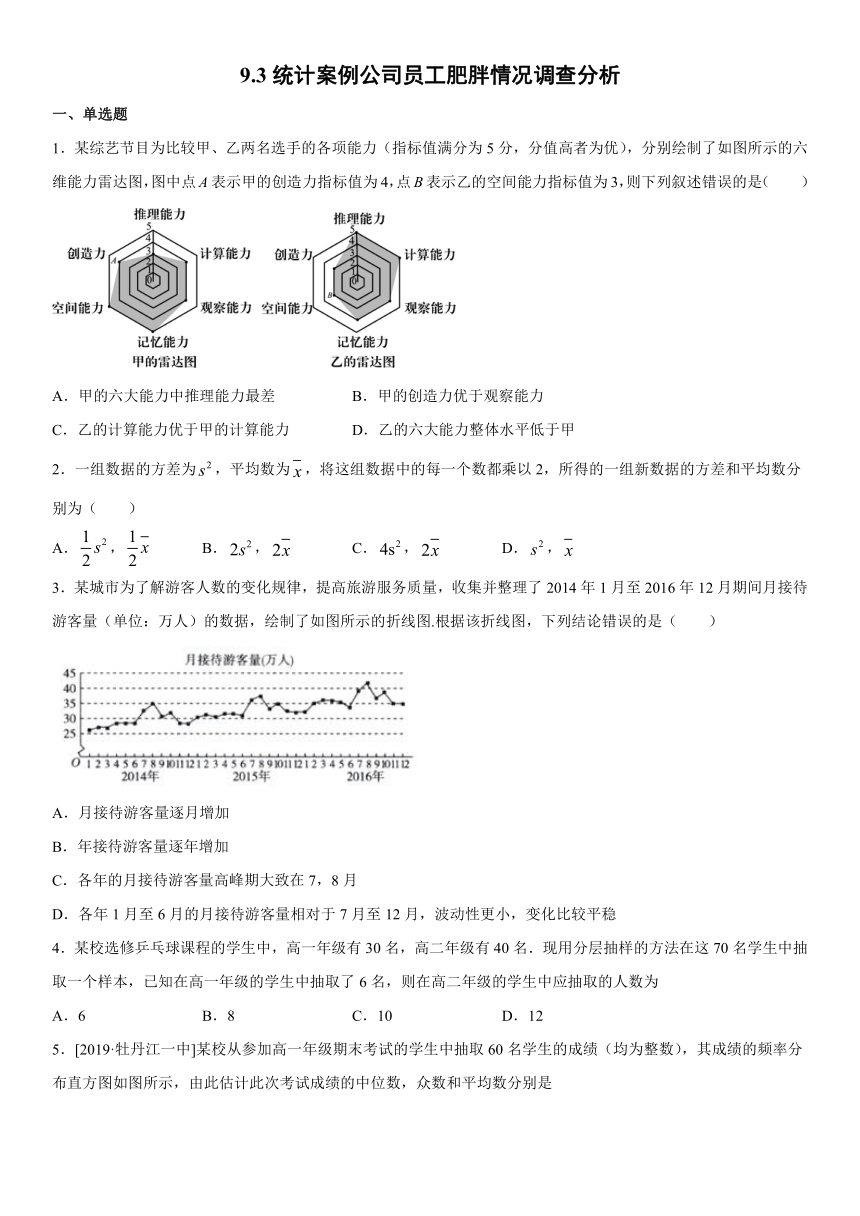
1.某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),分别绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下列叙述错误的是(
)
A.甲的六大能力中推理能力最差
B.甲的创造力优于观察能力
C.乙的计算能力优于甲的计算能力
D.乙的六大能力整体水平低于甲
2.一组数据的方差为,平均数为,将这组数据中的每一个数都乘以2,所得的一组新数据的方差和平均数分别为(
)
A.,
B.,
C.,
D.,
3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是(
)
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
4.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为
A.6
B.8
C.10
D.12
5.[2019·牡丹江一中]某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数和平均数分别是
A.73.3,75,72
B.73.3,80,73
C.70,70,76
D.70,75,75
6.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是
A.12.5;12.5
B.13;13
C.13;12.5
D.12.5;13
7.一个样本a,3,4,5,6的平均数是b,且不等式x2-6x+c<0的解集为(a,b),则这个样本的标准差是( )
A.1
B.
C.
D.2
8.对于数据3,3,2,3,6,3,10,3,6,3,2.
①这组数据的众数是3;
②这组数据的众数与中位数的数值不相等;
③这组数据的中位数与平均数的数值相等;
④这组数据的平均数与众数的值相等.
其中正确的结论的个数
A.1
B.2
C.3
D.4
9.一个样本的容量为,分成组,已知第一组、第三组的频数分别是、,第二、五组的频率都为,则该样本的中位数在
A.第二组
B.第三组
C.第四组
D.第五组
10.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
11.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为a,x4,x5,x6,…,x10的平均数为b,则样本数据的平均数为 ( )
A.
B.
C.
D.
12.某学校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是17.5,30],样本数据分组为17.5,20),20,22.5),22.5,25),25,27.5),27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是
A.56
B.60
C.140
D.120
13.某射手在一次训练中五次射击的成绩分别为9.4,9.4,9.4,9.6,9.7,则该射手五次射击的成绩的方差是 ( )
A.0.127
B.0.016
C.0.08
D.0.216
14.已知一组数据的平均数是2,方差是,那么数据的平均数和方差分别是(
)
A.2,
B.2,
3
C.4,
D.4,
3
15.2021年起,我市将试行“3+1+2”的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是(
)
A.甲的化学成绩领先年级平均分最多.
B.甲有2个科目的成绩低于年级平均分.
C.甲的成绩最好的前两个科目是化学和地理.
D.对甲而言,物理、化学、地理是比较理想的一种选科结果.
16.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数
B.平均数
C.方差
D.极差
17.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为
A.
B.
C.
D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、解答题
18.某校为了解全校高中学生五一假期参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.
(1)求这100名学生中参加实践活动时间在6~10小时的人数;
(2)估计这100名学生参加实践活动时间的众数、中位数和平均数.
19.甲、乙两种水稻试验品种连续5年的平均单位面积产量如下(单位:t/hm2),试根据这组数据估计哪一种水稻品种的产量比较稳定.
品种
第1年
第2年
第3年
第4年
第5年
甲
9.8
9.9
10.1
10
10.2
乙
9.4
10.3
10.8
9.7
9.8
20.对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图.
分组
频数
频率
[10,15)
10
0.25
[15,20)
24
n
[20,25)
m
p
[25,30]
2
0.05
合计
M
1
(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计这次学生参加社区服务人数的众数、中位数以及平均数.
21.某制造商月生产了一批乒乓球,随机抽样个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
分组
频数
频率
10
20
50
20
合计
100
(1)请在上表中补充完成频率分布表(结果保留两位小数),并在上图中画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间的中点值是作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
参考答案
1.B
2.C
3.A
4.B
5.A
6.D
7.B
8.A
9.B
10.A
11.B
12.C
13.B
14.D
15.A
16.A
17.C
18.(1)58;(2)众数7,中位数2,平均数7.16
19.甲种水稻的产量比较稳定
20.见解析
21.(1)见解析;(2)
40.00(mm)
9.3统计案例公司员工肥胖情况调查分析
一、单选题
1.某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),分别绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下列叙述错误的是(
)
A.甲的六大能力中推理能力最差
B.甲的创造力优于观察能力
C.乙的计算能力优于甲的计算能力
D.乙的六大能力整体水平低于甲
2.一组数据的方差为,平均数为,将这组数据中的每一个数都乘以2,所得的一组新数据的方差和平均数分别为(
)
A.,
B.,
C.,
D.,
3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是(
)
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
4.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为
A.6
B.8
C.10
D.12
5.[2019·牡丹江一中]某校从参加高一年级期末考试的学生中抽取60名学生的成绩(均为整数),其成绩的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数和平均数分别是
A.73.3,75,72
B.73.3,80,73
C.70,70,76
D.70,75,75
6.如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是
A.12.5;12.5
B.13;13
C.13;12.5
D.12.5;13
7.一个样本a,3,4,5,6的平均数是b,且不等式x2-6x+c<0的解集为(a,b),则这个样本的标准差是( )
A.1
B.
C.
D.2
8.对于数据3,3,2,3,6,3,10,3,6,3,2.
①这组数据的众数是3;
②这组数据的众数与中位数的数值不相等;
③这组数据的中位数与平均数的数值相等;
④这组数据的平均数与众数的值相等.
其中正确的结论的个数
A.1
B.2
C.3
D.4
9.一个样本的容量为,分成组,已知第一组、第三组的频数分别是、,第二、五组的频率都为,则该样本的中位数在
A.第二组
B.第三组
C.第四组
D.第五组
10.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
11.已知样本数据x1,x2,…,x10,其中x1,x2,x3的平均数为a,x4,x5,x6,…,x10的平均数为b,则样本数据的平均数为 ( )
A.
B.
C.
D.
12.某学校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是17.5,30],样本数据分组为17.5,20),20,22.5),22.5,25),25,27.5),27.5,30).根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是
A.56
B.60
C.140
D.120
13.某射手在一次训练中五次射击的成绩分别为9.4,9.4,9.4,9.6,9.7,则该射手五次射击的成绩的方差是 ( )
A.0.127
B.0.016
C.0.08
D.0.216
14.已知一组数据的平均数是2,方差是,那么数据的平均数和方差分别是(
)
A.2,
B.2,
3
C.4,
D.4,
3
15.2021年起,我市将试行“3+1+2”的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是(
)
A.甲的化学成绩领先年级平均分最多.
B.甲有2个科目的成绩低于年级平均分.
C.甲的成绩最好的前两个科目是化学和地理.
D.对甲而言,物理、化学、地理是比较理想的一种选科结果.
16.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
A.中位数
B.平均数
C.方差
D.极差
17.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为
A.
B.
C.
D.
第II卷(非选择题)
请点击修改第II卷的文字说明
二、解答题
18.某校为了解全校高中学生五一假期参加实践活动的情况,抽查了100名学生,统计他们假期参加实践活动的时间,绘成的频率分布直方图如图所示.
(1)求这100名学生中参加实践活动时间在6~10小时的人数;
(2)估计这100名学生参加实践活动时间的众数、中位数和平均数.
19.甲、乙两种水稻试验品种连续5年的平均单位面积产量如下(单位:t/hm2),试根据这组数据估计哪一种水稻品种的产量比较稳定.
品种
第1年
第2年
第3年
第4年
第5年
甲
9.8
9.9
10.1
10
10.2
乙
9.4
10.3
10.8
9.7
9.8
20.对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图.
分组
频数
频率
[10,15)
10
0.25
[15,20)
24
n
[20,25)
m
p
[25,30]
2
0.05
合计
M
1
(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计这次学生参加社区服务人数的众数、中位数以及平均数.
21.某制造商月生产了一批乒乓球,随机抽样个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
分组
频数
频率
10
20
50
20
合计
100
(1)请在上表中补充完成频率分布表(结果保留两位小数),并在上图中画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间的中点值是作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
参考答案
1.B
2.C
3.A
4.B
5.A
6.D
7.B
8.A
9.B
10.A
11.B
12.C
13.B
14.D
15.A
16.A
17.C
18.(1)58;(2)众数7,中位数2,平均数7.16
19.甲种水稻的产量比较稳定
20.见解析
21.(1)见解析;(2)
40.00(mm)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
