2020-2021学年 高二物理 动量守恒定律及守恒条件 期末复习强化学案Word版含答案
文档属性
| 名称 | 2020-2021学年 高二物理 动量守恒定律及守恒条件 期末复习强化学案Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 530.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-14 12:23:58 | ||
图片预览




文档简介
动量守恒定律及守恒条件
知识点一 动量守恒定律及守恒条件
1.动量守恒定律
(1)内容:如果一个系统________,或者所受外力的矢量和为0,这个系统的总动量保持不变.
(2)动量守恒定律的表达式:m1v1+m2v2=________________或Δp1=-Δp2.
2.系统动量守恒的条件
(1)理想守恒:系统不受外力或所受________的合力为零,则系统动量守恒.
(2)近似守恒:系统受到的合外力不为零,但当内力____________合外力时,系统的动量可近似看成守恒.
(3)分方向守恒:系统在某个方向上所受____________为零或该方向F内?F外时,系统在该方向上动量守恒.
知识点二 弹性碰撞和非弹性碰撞
1.碰撞
(1)概念:碰撞是指物体间的相互作用持续时间__________,而物体间相互作用力________的现象.
(2)特点:在碰撞现象中,一般都满足内力____________外力,可认为相互碰撞的系统动量守恒.
(3)分类
种类
动量是否守恒
机械能是否守恒
弹性碰撞
守恒
________
非弹性碰撞
守恒
有损失
完全非弹性碰撞
守恒
损失________
2.反冲运动
(1)定义:静止或运动的物体通过分离出部分物质,而使自身在反方向获得加速的现象.
(2)特点:在反冲运动中,如果没有外力作用或外力远小于物体间的相互作用力,系统的________是守恒的.
(3)爆炸现象:爆炸与碰撞类似,物体间的相互作用力很大,且____________系统所受的外力,所以系统动量________,爆炸过程中位移很小,可忽略不计,作用后从相互作用前的位置以新的动量开始运动.
思考辨析
(1)系统动量不变是指系统的动量大小和方向都不变.( )
(2)系统的动量守恒时,机械能也一定守恒.( )
(3)当质量相等时,发生完全弹性碰撞的两个球碰撞前后速度交换.( )
(4)光滑水平面上的两球做相向运动,发生正碰后两球均变为静止,于是可以断定碰撞前两球的动量大小一定相等.( )
教材改编
[人教版选修3-5P21T2改编]A球的质量是m,B球的质量是2m,它们在光滑的水平面上以相同的动量运动.B在前,A在后,发生正碰后,A球仍朝原方向运动,但其速率是原来的一半,碰后两球的速率比v′A:v′B为( )
A.1:2 B.1:3
C.2:1 D.2:3
考点一 动量守恒定律的理解与应用
师生共研
题型1|动量守恒的判断
例1 [2020·江西南昌新建一中月考]如图所示,用轻弹簧相连的物块A和B放在光滑的水平面上,物块A紧靠竖直墙壁,一颗子弹沿水平方向射入物块B并留在其中,在下列依次进行的四个过程中,由子弹、弹簧和A、B物块组成的系统,动量守恒,机械能也守恒的是( )
A.子弹射入物块B的过程
B.物块B和子弹一起向左运动的过程
C.弹簧推物块B向右运动,直到弹簧恢复原长的过程
D.弹簧恢复原长后,物块B因惯性继续向右运动,直到弹簧伸长最大的过程
题型2|动量守恒定律的基本应用
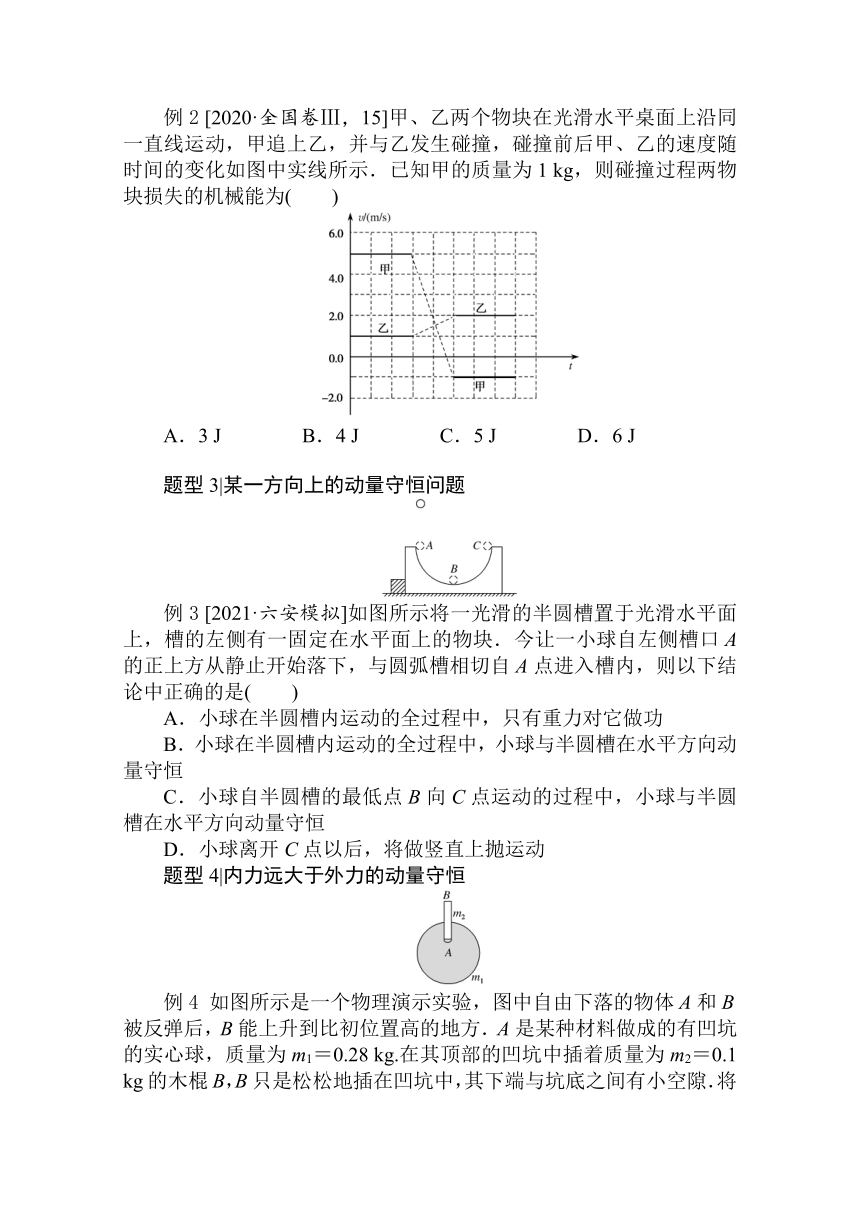
例2 [2020·全国卷Ⅲ,15]甲、乙两个物块在光滑水平桌面上沿同一直线运动,甲追上乙,并与乙发生碰撞,碰撞前后甲、乙的速度随时间的变化如图中实线所示.已知甲的质量为1 kg,则碰撞过程两物块损失的机械能为( )
A.3 J B.4 J C.5 J D.6 J
题型3|某一方向上的动量守恒问题
例3 [2021·六安模拟]如图所示将一光滑的半圆槽置于光滑水平面上,槽的左侧有一固定在水平面上的物块.今让一小球自左侧槽口A的正上方从静止开始落下,与圆弧槽相切自A点进入槽内,则以下结论中正确的是( )
A.小球在半圆槽内运动的全过程中,只有重力对它做功
B.小球在半圆槽内运动的全过程中,小球与半圆槽在水平方向动量守恒
C.小球自半圆槽的最低点B向C点运动的过程中,小球与半圆槽在水平方向动量守恒
D.小球离开C点以后,将做竖直上抛运动
题型4|内力远大于外力的动量守恒
例4 如图所示是一个物理演示实验,图中自由下落的物体A和B被反弹后,B能上升到比初位置高的地方.A是某种材料做成的有凹坑的实心球,质量为m1=0.28 kg.在其顶部的凹坑中插着质量为m2=0.1 kg的木棍B,B只是松松地插在凹坑中,其下端与坑底之间有小空隙.将此装置从A下端离地板的高度H=1.25 m处由静止释放,实验中,A触地后在极短时间内反弹,且其速度大小不变,接着木棍B脱离球A开始上升,而球A恰好停留在地板上,则反弹后木棍B上升的高度为(重力加速度g取10 m/s2)( )
A.4.05 m B.1.25 m C.5.30 m D.12.5 m
练1 (多选)如图所示,小车在光滑水平面上向左匀速运动,水平轻质弹簧左端固定在A点,物体与固定在A点的细线相连,弹簧处于压缩状态(物体与弹簧未连接).某时刻细线断了,物体沿车滑动到B端粘在B端的油泥上,取小车、物体和弹簧为一个系统,下列说法正确的是( )
A.若物体滑动中不受摩擦力,则该系统全过程机械能守恒
B.若物体滑动中有摩擦力,则该系统全过程动量守恒
C.不论物体滑动中有没有摩擦,小车的最终速度与断线前相同
D.不论物体滑动中有没有摩擦,系统损失的机械能相同
练2 [2020·全国卷Ⅱ,21](多选)水平冰面上有一固定的竖直挡板.一滑冰运动员面对挡板静止在冰面上,他把一质量为4.0 kg的静止物块以大小为5.0 m/s的速度沿与挡板垂直的方向推向挡板,运动员获得退行速度;物块与挡板弹性碰撞,速度反向,追上运动员时,运动员又把物块推向挡板,使其再一次以大小为5.0 m/s的速度与挡板弹性碰撞.总共经过8次这样推物块后,运动员退行速度的大小大于5.0 m/s,反弹的物块不能再追上运动员.不计冰面的摩擦力,该运动员的质量可能为( )
A.48 kg B.53 kg C.58 kg D.63 kg
练3 [易错题]如图所示,在光滑水平面上有A、B两辆小车,水平面左侧有一竖直墙,在车B上坐着一个小孩,车B与小孩的总质量是车A质量的4倍.从静止开始,小孩把车A以速度v(对地)推出,车A返回后,小孩抓住并再次把它推出,每次推出车A的速度都是v(对地)、方向向左,则小孩把车A总共推出多少次后,车A返回时,小孩不能再接到车A.(小车与竖直墙相撞无能量损失)
题后反思
1.动量守恒定律常用的三种表达形式
(1)m1v1+m2v2=m1v′1+m2v′2,相互作用的两个物体组成的系统,作用前的动量矢量和等于作用后的动量矢量和.
(2)Δp1=-Δp2,相互作用的两个物体动量的增量等大反向.
(3)Δp=0,系统总动量的增量为零.
2.应用动量守恒定律解题的基本步骤
考点二 碰撞问题
多维探究
题型1|碰撞的可能性问题
碰撞后运动状态可能性判断的三个依据
(1)动量守恒:p1+p2=p′1+p′2.
(2)动能不增加:Ek1+Ek2≥E′k1+E′k2或p122m1+p222m2≥p'122m1+p'222m2.
(3)速度要符合情景.
①若碰前两物体同向运动,则应有v后>v前,碰后原来在前的物体速度一定增大,若碰后两物体同向运动,则应有v′前≥v′后.
②碰前两物体相向运动,碰后两物体的运动方向不可能都不改变.
例5 (多选)质量分别为mP=1 kg、mQ=2 kg的小球P、Q静止在光滑的水平面上,现给小球P以水平的速度vP0=4 m/s沿直线朝小球Q运动,并发生正碰,分别用vP、vQ表示两小球碰撞结束的速度.则关于vP、vQ的大小可能的是( )
A.vP=vQ=43 m/s
B.vP=-1 m/s,vQ=2.5 m/s
C.vP=1 m/s,vQ=3 m/s
D.vP=-4 m/s,vQ=4 m/s
题型2弹性碰撞模型
弹性碰撞
动量守恒、机械能守恒m1v1+m2v2=m1v′1+m2v′212m1v12+12m2v22=12m1v'12+12m2v'22
例6如图,水平面上相距为L=5 m的P、Q两点分别固定一竖直挡板,一质量为M=2 kg的小物块B静止在O点,OP段光滑,OQ段粗糙且长度为d=3 m.一质量为m=1 kg的小物块A以v0=6 m/s的初速度从OP段的某点向右运动,并与B发生弹性碰撞。两物块与OQ段间的动摩擦因数均为μ=0.2,两物块与挡板的碰撞时间极短且均不损失机械能。重力加速度g取10 m/s2,求:
(1)A与B在O点碰后瞬间各自的速度;
(2)两物块各自停止运动时的时间间隔.
题型3|完全非弹性碰撞模型
完全非弹
性碰撞
动量守恒、机械能损失最多
m1v1+m2v2=(m1+m2)v
ΔE=12m1v12+12m2v22-12 (m1+m2)v2
例7 如图所示,某超市两辆相同的手推购物车质量均为10 kg,相距为3 m沿直线排列,静置于水平地面上.为了节省收纳空间,工人给第一辆车一个瞬间的水平推力使其运动,并与第二辆车相碰,且在极短时间内相互嵌套结为一体,以共同的速度运动了1 m,恰好停靠在墙边.若车运动时受到的摩擦力恒为车重力的0.2,忽略空气阻力,重力加速度g=10 m/s2.求:
(1)购物车碰撞过程中系统损失的机械能;
(2)工人给第一辆购物车的水平冲量大小.
练4 如图所示,竖直平面内的四分之一光滑圆弧轨道下端与光滑水平桌面相切,小滑块B静止在圆弧轨道的最低点.现将小滑块A从圆弧轨道的最高点无初速度释放.已知圆弧轨道半径R=1.8 m,小滑块的质量关系是mB=2mA,重力加速度g=10 m/s2.则碰后小滑块B的速度大小不可能是( )
A.5 m/s B.4 m/s C.3 m/s D.2 m/s
练5 打羽毛球是一种常见的体育健身活动.当羽毛球以5 m/s的速度水平飞来时,运动员迅速挥拍以10 m/s的水平速度迎面击球,假设羽毛球和羽毛球拍的碰撞为弹性碰撞,且球拍的质量远大于球的质量,羽毛球反弹的速度大小为( )
A.25 m/s B.20 m/s C.15 m/s D.5 m/s
考点三 “反冲”和“爆炸”模型
多维探究
题型1| “反冲”模型
作用
原理
反冲运动是系统内物体之间的作用力和反作用力产生的效果
动量
守恒
反冲运动中系统不受外力或内力远大于外力,所以反冲运动遵循动量守恒定律
机械能
增加
反冲运动中,由于有其他形式的能转化为机械能,所以系统的总机械能增加
例8[2021·山东淄博一模]新型冠状病毒主要传播方式为飞沫传播,打喷嚏可以将飞沫喷到十米之外.有关专家研究得出打喷嚏时气流喷出的速度可达40 m/s,假设打一次喷嚏大约喷出50 mL的气体,用时约为0.02 s.已知空气的密度为1.3 kg/m3,估算打一次喷嚏人受到的平均反冲力为( )
A.13 N B.0.13 N C.0.68 N D.2.6 N
题型2| “人船”模型的应用
1.模型特点
2.结论:m1x1=m2x2(m1、m2为相互作用的物体质量,x1、x2为其位移大小)
例9 [2021·湖南长沙九中月考]如图所示,质量为m的人在质量为M的平板车上从左端走到右端,若不计平板车与地面间的摩擦,则下列说法正确的是( )
A.人在车上行走时,车将向右运动
B.当人停止走动时,由于车的惯性大,车将继续后退
C.若人越慢地从车的左端走到右端,则车在地面上移动的距离越大
D. 不管人在车上行走的速度多大,车在地面上移动的距离都相同
题型3| “爆炸”模型
动量守恒
爆炸物体间的相互作用力远远大于受到的外力,所以在爆炸过程中,系统的总动量守恒
动能增加
在爆炸过程中,有其他形式的能量(如化学能)转化为动能
位置不变
爆炸的时间极短,因而作用过程中物体产生的位移很小,可以认为爆炸后各部分仍然从爆炸前的位置以新的动量开始运动
例10 [2021·山西太原五中月考]如图所示,光滑水平面上静止着两个滑块A、B,mA=0.5 kg、mB=1 kg,两滑块间夹有少量炸药,点燃炸药后其化学能全部转化为滑块A、B的动能,滑块A向左恰好能通过半圆轨道的最高点,滑块B向右冲上倾角为37°的斜面,到达高度h=0.6 m后返回水平面,已知半圆轨道半径R=0.72 m,滑块B与斜面间的动摩擦因数μ=0.5,水平面与斜面平滑连接,滑块B经连接处时机械能无损失,重力加速度g=10 m/s2(sin 37°=0.6,cos 37°=0.8).求:
(1)滑块B第一次返回水平面的速度大小;
(2)炸药点燃后释放的化学能;
(3)滑块A第一次通过半圆轨道克服阻力做功大小.
练6 [2021·福建三明一中月考]有一个质量为3m的爆竹斜向上抛出,到达最高点时速度大小为v0、方向水平向右,在最高点爆炸成质量不等的两块,其中一块质量为2m,速度大小为v,方向水平向右,则另一块的速度是( )
A.3v0-v B.2v0-3v
C.3v0-2v D.2v0+v
练7 [2021·江西名校月考]如图所示,长为l的轻绳,一端用质量为m的圆环套在水平光滑的横杆上,另一端连接一质量为2m的小球.开始时,将小球移至横杆处(轻绳处于水平伸直状态),然后轻轻放手,当轻绳与横杆成直角时,小球速度沿水平方向且大小是v,此过程圆环的位移是x,则( )
A.v=2gl3,x=23l B.v=gl3,x=23l
C.v=gl,x=0 D.v= 2gl3,x=13l
第2讲 动量守恒定律及守恒条件
基础落实
知识点一
1.(1)不受外力 (2)m1v′1+m2v′2
2.(1)外力 (2)远大于 (3)合外力
知识点二
1.(1)很短 很大 (2)远大于 (3)守恒 最大
2.(2) 动量 (3)远大于 守恒
思考辨析
1.答案:(1)√ (2)× (3)√ (4)√
教材改编
解析:设碰前A球的速率为v,根据题意pA=pB,即mv=2mvB,得碰前vB=v2,碰后v′A=v2,由动量守恒定律,有mv+2m×v2=m×v2+2mv′B,解得v′B=3v4,所以vA'∶v′B=v2∶3v4=23,D正确.
答案:D
考点突破
例1 解析:本题考查子弹打物块模型与弹簧的结合.子弹射入物块B的过程,由于时间极短,子弹与物块B组成的系统动量守恒,在此运动过程中,子弹的动能有一部分转化为系统的内能,则系统的机械能减小,所以系统的机械能不守恒,A错误;物块B和子弹一起向左运动的过程,系统受到墙壁的作用力,合外力不为零,则系统的动量不守恒,在此运动过程中,只有弹簧的弹力做功,所以系统的机械能守恒,B错误;弹簧推物块B向右运动,直到弹簧恢复原长的过程中,弹簧要恢复原长,墙壁对弹簧有向右的弹力,系统所受的合外力不为零,则系统的动量不守恒,在此运动过程中,只有弹簧的弹力做功,所以系统的机械能守恒,C错误;弹簧恢复原长后,物块A离开墙壁,物块B继续向右运动,系统所受的合外力为零,则系统的动量守恒,在此过程中只有弹簧的弹力做功,所以系统的机械能也守恒,D正确.
答案:D
例2 解析:由图象可知甲物块碰前速度v甲=5 m/s,乙物块碰前速度v乙=1 m/s,甲物块碰后速度v′甲=-1 m/s,乙物块碰后速度v′乙=2 m/s.甲和乙碰撞过程中系统动量守恒,有m甲v甲+m乙v乙=m甲v′甲+m乙v′乙,解得m乙=6 kg.碰撞过程中两物块损失的机械能
ΔE=12m甲v甲2+12 m乙v乙2-12m甲v甲′2-12m乙v乙′2=3 J.故选A项.
答案:A
例3 解析:当小球在槽内由A运动到B的过程中,左侧物块对槽有作用力,小球与槽组成的系统水平方向上的动量不守恒,故B错误;当小球由B运动到C的过程中,因小球对槽有斜向右下方的压力,槽做加速运动,动能增加,小球机械能减少,槽对小球的支持力对小球做了负功,故A错误;小球从B到C的过程中,系统水平方向所受合外力为零,满足系统水平方向动量守恒,故C正确;小球离开C点以后,既有竖直向上的分速度,又有水平分速度,小球做斜上抛运动,故D错误.
答案:C
例4 解析:由题意可知,A、B做自由落体运动,由v2=2gH,可得A、B的落地速度的大小v=2gH,A反弹后与B的碰撞为瞬时作用,A、B组成的系统在竖直方向上所受合力虽然不为零,但作用时间很短,系统的内力远大于外力,所以动量近似守恒,故有m1v-m2v=0+m2v′2,B上升高度h=v2'2 2g,联立并代入数据得h=4.05 m,A正确.
答案:A
练1 解析:物体与油泥粘合的过程,发生非弹性碰撞,系统机械能有损失,故A错误;整个系统在水平方向不受外力,竖直方向上合外力为零,则系统动量一直守恒,故B正确;取系统的初速度方向为正方向,根据动量守恒定律可知,物体在沿车滑动到B端粘在B端的油泥上后系统共同的速度与初速度是相同的,故C正确;由C的分析可知,当物体与B端油泥粘在一起时,系统的速度与初速度相等,所以系统的末动能与初动能是相等的,系统损失的机械能等于弹簧的弹性势能,与物体滑动中有没有摩擦无关,故D正确.
答案:BCD
练2 解析:物块每次与挡板碰撞后,挡板对物块的冲量I冲=mv0-m(-v0)=40 kg·m·s-1,方向与运动员退行方向相同,以此方向为正方向,以运动员和物块整体为研究对象,当物块撞击挡板7次后,7I冲=m人v7+mv0,v7<5 m/s,得m人>52 kg,当物块撞击挡板8次后,8I冲=m人v8+mv0,v8>5 m/s,得m人<60 kg.故B、C正确,A、D错误.
答案:BC
练3 解析:设小孩把车A总共推出n次后,车A返回时,小孩恰好不能再接到小车A.此时,车A返回时的速度v与车B的速度恰好相等,即vB=v①
第1次推车时,小孩和车B获得的动量为mAv,以后每次推车时获得的动量为2mAv,根据动量守恒定律得
mAv+(n-1)·2mAv=mBvB②
又由题意知4mA=mB③
联立①②③解得n=2.5,
所以小孩把车A总共推出3次后,车A返回时,小孩不能再接到小车A.
答案:3次
例5 解析:碰撞前总动量为p=mPvP0=4 kg·m/s,碰撞前总动能为Ek=12mPvP02=8 J.如果vP=vQ=43 m/s,p′=mPvP+mQvQ=4 kg·m/s,E′k=12mPvP2+12mQvQ2=83 J,碰撞过程动量守恒,能量不增加,A正确;如果vP=-1 m/s,vQ=2.5 m/s,p′=mPvP+mQvQ=4 kg·m/s,E′k=12mPvP2+12mQvQ2=6.75 J,能量不增加,碰撞过程动量守恒,B正确;如果vP=1 m/s,vQ=3 m/s,p′=mPvP+mQvQ=7 kg·m/s,碰撞过程动量不守恒,C错误;如果vP=-4 m/s,vQ=4 m/s,p′=mPvP+mQvQ=4 kg·m/s,E′k=12mPvP2+12mQvQ2=24 J,碰撞过程动量守恒,动能增加,D错误.
答案:AB
例6 解析:(1)设A、B在O点碰后的速度分别为v1和v2,以向右为正方向.由动量守恒定律得:mv0=mv1+Mv2.碰撞前后动能相等,则得:12mv02=12mv12+12Mv22,解得:v1=-2 m/s,方向向左,v2=4 m/s,方向向右.
(2)碰后,两物块在OQ段减速时加速度大小均为:a=μg=2 m/s2.B经过t1时间与Q处挡板相碰,由运动学公式:v2t1-12at12=d,得:t1=1 s(t1=3 s舍去).与挡板碰后,B的速度大小v3=v2-at1=2 m/s,反弹后减速时间t2=v3a=1 s,反弹后经过位移s1=v32 2a=1 m,B停止运动.物块A与P处挡板碰后,以v4=2 m/s的速度滑上O点,经过s2=v42 2a=1 m停止.所以最终A、B的距离s=d-s1-s2=1 m,两者不会碰第二次.在A、B碰后,A运动总时间tA=2L-dv1+v4a=3 s,B运动总时间 tB=t1+t2=2 s,则时间间隔ΔtAB=tA-tB=1 s.
答案:(1)2 m/s,方向向左 4 m/s,方向向右 (2)1 s
例7 解析:(1)设第一辆车碰前瞬间的速度为v1,碰前两车间距为L1,与第二辆车碰后的共同速度为v2,共同移动的距离为L2,由动量守恒定律有mv1=2mv2
由动能定理有-0.2×2mgL2=0-122mv22
则碰撞中系统损失的机械能ΔE=12mv12-122mv22
联立解得ΔE=40 J
(2)设第一辆车推出时的速度为v0
由动能定理有-0.2mgL1=12mv12-12mv02
第一辆车的水平冲量大小I=mv0
联立解得I=207 N·s
答案:(1)40 J (2)207 N·s
练4 解析:滑块A下滑过程,由机械能守恒定律得mAgR=12mAv02 ,解得v0=6 m/s.若两个滑块发生的是弹性碰撞,取向右为正方向,由动量守恒定律和机械能守恒定律得mAv0=mAvA+mBvB,12mAv02=12mAvA2+12mBvB2,解得vB=4 m/s.若两个滑块发生的是完全非弹性碰撞,由动量守恒定律得mAv0=(mA+mB)v′B,解得v′B=2 m/s.所以碰后小滑块B的速度范围为2 m/s≤vB≤4 m/s,不可能为5 m/s.
答案:A
练5 解析:设碰撞前羽毛球和羽毛球拍的速度分别为v1和v2,碰后羽毛球和羽毛球拍的速度分别为v′1和v′2.取碰撞前羽毛球的速度方向为正方向,根据动量守恒定律和机械能守恒定律得
m1v1+m2v2=m1v′1+m2v2′.①
12m1v12+12m2v22=12m1v1'2+12m2v2'2.②
联立解得v′1=m1-m2v1+2m2v2m1+m2
据题有m1?m2,
则得v′1=2v2-v1=[2×10-(-5)] m/s=25 m/s.
答案:A
例8 解析:本题考查反冲运动,打一次喷嚏大约喷出气体的质量m=ρV,由动量定理得FΔt=mv,解得F=mvΔt=ρVvΔt=1.3×50×10-6×400.02 N=0.13 N,根据牛顿第三定律可知,打一次喷嚏人受到的平均反冲力为0.13 N,故选B.
答案:B
例9 解析:本题考查“人船模型”.人与平板车组成的系统动量守恒,由动量守恒定律得mv人+Mv车=0,故平板车运动的方向一定与人运动的方向相反,故人与平板车的速度方向相反,人在车上向右行走时,车将向左运动,A错误;因人与平板车的总动量为零,故人停止走动,速度为零时,车的速度也为零,B错误;因人与车的运动时间相等,动量守恒,以人行走的方向为正方向,则mx人-Mx车=0,故车与人的位移之比为x车x人=mM,则车的位移与人的运动速度无关,不论人的速度多大,车在地面上移动的距离都相等,C错误,D正确.
答案:D
例10 解析:本题考查动能定理、动量守恒定律和能量守恒定律.(1)设滑块B返回水平面的速度大小为v′B,在斜面上运动的最大距离为L,则L=hsin37°,滑块B从斜面最高点返回水平面,由动能定理得(mBg sin 37°-μmBg cos 37°)L=12mBvB'2-0,联立解得v′B=2 m/s.
(2)设滑块B滑上斜面的初速度大小为vB,滑块B从水平面滑到斜面最高点,由动能定理得-(mBg sin 37°+μmBg cos 37°)L=0-12mBvB2,点燃炸药后,由动量守恒定律得mAvA-mBvB=0,由能量守恒定律得E=12mAvA2+12mBvB2,联立解得E=30 J.
(3)滑块A恰好到达半圆轨道的最高点,有mAg=mAvA'2 R,由动能定理得-2mAgR-Wf=12mAvA'2-12mAvA2,联立解得Wf=11 J.
答案:(1)2 m/s (2)30 J (3)11 J
练6 解析:本题考查爆炸中的动量守恒问题.爆竹在最高点速度大小为v0、方向水平向右,爆炸前动量为3mv0,其中一块质量为2m,速度大小为v,方向水平向右,设爆炸后另一块瞬时速度大小为v′,取爆竹到最高点未爆炸前的速度方向为正方向,爆炸过程动量守恒,则3mv0=2mv+mv′,解得v′=3v0-2v,C正确,A、B、D错误.
答案:C
练7 解析:本题考查动量守恒定律、机械能守恒定律.设当轻绳与横杆成直角时,圆环的速度为v1,根据圆环、小球组成的系统在水平方向动量守恒,则有2mv=mv1,由于机械能守恒,则有2mgl=12(2m)v2+12mv12,联立解得v=23gl,圆环、小球运动的时间相等,则有2m(l-x)=mx,解得x=23l,A正确,B、C、D错误.
答案:A
知识点一 动量守恒定律及守恒条件
1.动量守恒定律
(1)内容:如果一个系统________,或者所受外力的矢量和为0,这个系统的总动量保持不变.
(2)动量守恒定律的表达式:m1v1+m2v2=________________或Δp1=-Δp2.
2.系统动量守恒的条件
(1)理想守恒:系统不受外力或所受________的合力为零,则系统动量守恒.
(2)近似守恒:系统受到的合外力不为零,但当内力____________合外力时,系统的动量可近似看成守恒.
(3)分方向守恒:系统在某个方向上所受____________为零或该方向F内?F外时,系统在该方向上动量守恒.
知识点二 弹性碰撞和非弹性碰撞
1.碰撞
(1)概念:碰撞是指物体间的相互作用持续时间__________,而物体间相互作用力________的现象.
(2)特点:在碰撞现象中,一般都满足内力____________外力,可认为相互碰撞的系统动量守恒.
(3)分类
种类
动量是否守恒
机械能是否守恒
弹性碰撞
守恒
________
非弹性碰撞
守恒
有损失
完全非弹性碰撞
守恒
损失________
2.反冲运动
(1)定义:静止或运动的物体通过分离出部分物质,而使自身在反方向获得加速的现象.
(2)特点:在反冲运动中,如果没有外力作用或外力远小于物体间的相互作用力,系统的________是守恒的.
(3)爆炸现象:爆炸与碰撞类似,物体间的相互作用力很大,且____________系统所受的外力,所以系统动量________,爆炸过程中位移很小,可忽略不计,作用后从相互作用前的位置以新的动量开始运动.
思考辨析
(1)系统动量不变是指系统的动量大小和方向都不变.( )
(2)系统的动量守恒时,机械能也一定守恒.( )
(3)当质量相等时,发生完全弹性碰撞的两个球碰撞前后速度交换.( )
(4)光滑水平面上的两球做相向运动,发生正碰后两球均变为静止,于是可以断定碰撞前两球的动量大小一定相等.( )
教材改编
[人教版选修3-5P21T2改编]A球的质量是m,B球的质量是2m,它们在光滑的水平面上以相同的动量运动.B在前,A在后,发生正碰后,A球仍朝原方向运动,但其速率是原来的一半,碰后两球的速率比v′A:v′B为( )
A.1:2 B.1:3
C.2:1 D.2:3
考点一 动量守恒定律的理解与应用
师生共研
题型1|动量守恒的判断
例1 [2020·江西南昌新建一中月考]如图所示,用轻弹簧相连的物块A和B放在光滑的水平面上,物块A紧靠竖直墙壁,一颗子弹沿水平方向射入物块B并留在其中,在下列依次进行的四个过程中,由子弹、弹簧和A、B物块组成的系统,动量守恒,机械能也守恒的是( )
A.子弹射入物块B的过程
B.物块B和子弹一起向左运动的过程
C.弹簧推物块B向右运动,直到弹簧恢复原长的过程
D.弹簧恢复原长后,物块B因惯性继续向右运动,直到弹簧伸长最大的过程
题型2|动量守恒定律的基本应用
例2 [2020·全国卷Ⅲ,15]甲、乙两个物块在光滑水平桌面上沿同一直线运动,甲追上乙,并与乙发生碰撞,碰撞前后甲、乙的速度随时间的变化如图中实线所示.已知甲的质量为1 kg,则碰撞过程两物块损失的机械能为( )
A.3 J B.4 J C.5 J D.6 J
题型3|某一方向上的动量守恒问题
例3 [2021·六安模拟]如图所示将一光滑的半圆槽置于光滑水平面上,槽的左侧有一固定在水平面上的物块.今让一小球自左侧槽口A的正上方从静止开始落下,与圆弧槽相切自A点进入槽内,则以下结论中正确的是( )
A.小球在半圆槽内运动的全过程中,只有重力对它做功
B.小球在半圆槽内运动的全过程中,小球与半圆槽在水平方向动量守恒
C.小球自半圆槽的最低点B向C点运动的过程中,小球与半圆槽在水平方向动量守恒
D.小球离开C点以后,将做竖直上抛运动
题型4|内力远大于外力的动量守恒
例4 如图所示是一个物理演示实验,图中自由下落的物体A和B被反弹后,B能上升到比初位置高的地方.A是某种材料做成的有凹坑的实心球,质量为m1=0.28 kg.在其顶部的凹坑中插着质量为m2=0.1 kg的木棍B,B只是松松地插在凹坑中,其下端与坑底之间有小空隙.将此装置从A下端离地板的高度H=1.25 m处由静止释放,实验中,A触地后在极短时间内反弹,且其速度大小不变,接着木棍B脱离球A开始上升,而球A恰好停留在地板上,则反弹后木棍B上升的高度为(重力加速度g取10 m/s2)( )
A.4.05 m B.1.25 m C.5.30 m D.12.5 m
练1 (多选)如图所示,小车在光滑水平面上向左匀速运动,水平轻质弹簧左端固定在A点,物体与固定在A点的细线相连,弹簧处于压缩状态(物体与弹簧未连接).某时刻细线断了,物体沿车滑动到B端粘在B端的油泥上,取小车、物体和弹簧为一个系统,下列说法正确的是( )
A.若物体滑动中不受摩擦力,则该系统全过程机械能守恒
B.若物体滑动中有摩擦力,则该系统全过程动量守恒
C.不论物体滑动中有没有摩擦,小车的最终速度与断线前相同
D.不论物体滑动中有没有摩擦,系统损失的机械能相同
练2 [2020·全国卷Ⅱ,21](多选)水平冰面上有一固定的竖直挡板.一滑冰运动员面对挡板静止在冰面上,他把一质量为4.0 kg的静止物块以大小为5.0 m/s的速度沿与挡板垂直的方向推向挡板,运动员获得退行速度;物块与挡板弹性碰撞,速度反向,追上运动员时,运动员又把物块推向挡板,使其再一次以大小为5.0 m/s的速度与挡板弹性碰撞.总共经过8次这样推物块后,运动员退行速度的大小大于5.0 m/s,反弹的物块不能再追上运动员.不计冰面的摩擦力,该运动员的质量可能为( )
A.48 kg B.53 kg C.58 kg D.63 kg
练3 [易错题]如图所示,在光滑水平面上有A、B两辆小车,水平面左侧有一竖直墙,在车B上坐着一个小孩,车B与小孩的总质量是车A质量的4倍.从静止开始,小孩把车A以速度v(对地)推出,车A返回后,小孩抓住并再次把它推出,每次推出车A的速度都是v(对地)、方向向左,则小孩把车A总共推出多少次后,车A返回时,小孩不能再接到车A.(小车与竖直墙相撞无能量损失)
题后反思
1.动量守恒定律常用的三种表达形式
(1)m1v1+m2v2=m1v′1+m2v′2,相互作用的两个物体组成的系统,作用前的动量矢量和等于作用后的动量矢量和.
(2)Δp1=-Δp2,相互作用的两个物体动量的增量等大反向.
(3)Δp=0,系统总动量的增量为零.
2.应用动量守恒定律解题的基本步骤
考点二 碰撞问题
多维探究
题型1|碰撞的可能性问题
碰撞后运动状态可能性判断的三个依据
(1)动量守恒:p1+p2=p′1+p′2.
(2)动能不增加:Ek1+Ek2≥E′k1+E′k2或p122m1+p222m2≥p'122m1+p'222m2.
(3)速度要符合情景.
①若碰前两物体同向运动,则应有v后>v前,碰后原来在前的物体速度一定增大,若碰后两物体同向运动,则应有v′前≥v′后.
②碰前两物体相向运动,碰后两物体的运动方向不可能都不改变.
例5 (多选)质量分别为mP=1 kg、mQ=2 kg的小球P、Q静止在光滑的水平面上,现给小球P以水平的速度vP0=4 m/s沿直线朝小球Q运动,并发生正碰,分别用vP、vQ表示两小球碰撞结束的速度.则关于vP、vQ的大小可能的是( )
A.vP=vQ=43 m/s
B.vP=-1 m/s,vQ=2.5 m/s
C.vP=1 m/s,vQ=3 m/s
D.vP=-4 m/s,vQ=4 m/s
题型2弹性碰撞模型
弹性碰撞
动量守恒、机械能守恒m1v1+m2v2=m1v′1+m2v′212m1v12+12m2v22=12m1v'12+12m2v'22
例6如图,水平面上相距为L=5 m的P、Q两点分别固定一竖直挡板,一质量为M=2 kg的小物块B静止在O点,OP段光滑,OQ段粗糙且长度为d=3 m.一质量为m=1 kg的小物块A以v0=6 m/s的初速度从OP段的某点向右运动,并与B发生弹性碰撞。两物块与OQ段间的动摩擦因数均为μ=0.2,两物块与挡板的碰撞时间极短且均不损失机械能。重力加速度g取10 m/s2,求:
(1)A与B在O点碰后瞬间各自的速度;
(2)两物块各自停止运动时的时间间隔.
题型3|完全非弹性碰撞模型
完全非弹
性碰撞
动量守恒、机械能损失最多
m1v1+m2v2=(m1+m2)v
ΔE=12m1v12+12m2v22-12 (m1+m2)v2
例7 如图所示,某超市两辆相同的手推购物车质量均为10 kg,相距为3 m沿直线排列,静置于水平地面上.为了节省收纳空间,工人给第一辆车一个瞬间的水平推力使其运动,并与第二辆车相碰,且在极短时间内相互嵌套结为一体,以共同的速度运动了1 m,恰好停靠在墙边.若车运动时受到的摩擦力恒为车重力的0.2,忽略空气阻力,重力加速度g=10 m/s2.求:
(1)购物车碰撞过程中系统损失的机械能;
(2)工人给第一辆购物车的水平冲量大小.
练4 如图所示,竖直平面内的四分之一光滑圆弧轨道下端与光滑水平桌面相切,小滑块B静止在圆弧轨道的最低点.现将小滑块A从圆弧轨道的最高点无初速度释放.已知圆弧轨道半径R=1.8 m,小滑块的质量关系是mB=2mA,重力加速度g=10 m/s2.则碰后小滑块B的速度大小不可能是( )
A.5 m/s B.4 m/s C.3 m/s D.2 m/s
练5 打羽毛球是一种常见的体育健身活动.当羽毛球以5 m/s的速度水平飞来时,运动员迅速挥拍以10 m/s的水平速度迎面击球,假设羽毛球和羽毛球拍的碰撞为弹性碰撞,且球拍的质量远大于球的质量,羽毛球反弹的速度大小为( )
A.25 m/s B.20 m/s C.15 m/s D.5 m/s
考点三 “反冲”和“爆炸”模型
多维探究
题型1| “反冲”模型
作用
原理
反冲运动是系统内物体之间的作用力和反作用力产生的效果
动量
守恒
反冲运动中系统不受外力或内力远大于外力,所以反冲运动遵循动量守恒定律
机械能
增加
反冲运动中,由于有其他形式的能转化为机械能,所以系统的总机械能增加
例8[2021·山东淄博一模]新型冠状病毒主要传播方式为飞沫传播,打喷嚏可以将飞沫喷到十米之外.有关专家研究得出打喷嚏时气流喷出的速度可达40 m/s,假设打一次喷嚏大约喷出50 mL的气体,用时约为0.02 s.已知空气的密度为1.3 kg/m3,估算打一次喷嚏人受到的平均反冲力为( )
A.13 N B.0.13 N C.0.68 N D.2.6 N
题型2| “人船”模型的应用
1.模型特点
2.结论:m1x1=m2x2(m1、m2为相互作用的物体质量,x1、x2为其位移大小)
例9 [2021·湖南长沙九中月考]如图所示,质量为m的人在质量为M的平板车上从左端走到右端,若不计平板车与地面间的摩擦,则下列说法正确的是( )
A.人在车上行走时,车将向右运动
B.当人停止走动时,由于车的惯性大,车将继续后退
C.若人越慢地从车的左端走到右端,则车在地面上移动的距离越大
D. 不管人在车上行走的速度多大,车在地面上移动的距离都相同
题型3| “爆炸”模型
动量守恒
爆炸物体间的相互作用力远远大于受到的外力,所以在爆炸过程中,系统的总动量守恒
动能增加
在爆炸过程中,有其他形式的能量(如化学能)转化为动能
位置不变
爆炸的时间极短,因而作用过程中物体产生的位移很小,可以认为爆炸后各部分仍然从爆炸前的位置以新的动量开始运动
例10 [2021·山西太原五中月考]如图所示,光滑水平面上静止着两个滑块A、B,mA=0.5 kg、mB=1 kg,两滑块间夹有少量炸药,点燃炸药后其化学能全部转化为滑块A、B的动能,滑块A向左恰好能通过半圆轨道的最高点,滑块B向右冲上倾角为37°的斜面,到达高度h=0.6 m后返回水平面,已知半圆轨道半径R=0.72 m,滑块B与斜面间的动摩擦因数μ=0.5,水平面与斜面平滑连接,滑块B经连接处时机械能无损失,重力加速度g=10 m/s2(sin 37°=0.6,cos 37°=0.8).求:
(1)滑块B第一次返回水平面的速度大小;
(2)炸药点燃后释放的化学能;
(3)滑块A第一次通过半圆轨道克服阻力做功大小.
练6 [2021·福建三明一中月考]有一个质量为3m的爆竹斜向上抛出,到达最高点时速度大小为v0、方向水平向右,在最高点爆炸成质量不等的两块,其中一块质量为2m,速度大小为v,方向水平向右,则另一块的速度是( )
A.3v0-v B.2v0-3v
C.3v0-2v D.2v0+v
练7 [2021·江西名校月考]如图所示,长为l的轻绳,一端用质量为m的圆环套在水平光滑的横杆上,另一端连接一质量为2m的小球.开始时,将小球移至横杆处(轻绳处于水平伸直状态),然后轻轻放手,当轻绳与横杆成直角时,小球速度沿水平方向且大小是v,此过程圆环的位移是x,则( )
A.v=2gl3,x=23l B.v=gl3,x=23l
C.v=gl,x=0 D.v= 2gl3,x=13l
第2讲 动量守恒定律及守恒条件
基础落实
知识点一
1.(1)不受外力 (2)m1v′1+m2v′2
2.(1)外力 (2)远大于 (3)合外力
知识点二
1.(1)很短 很大 (2)远大于 (3)守恒 最大
2.(2) 动量 (3)远大于 守恒
思考辨析
1.答案:(1)√ (2)× (3)√ (4)√
教材改编
解析:设碰前A球的速率为v,根据题意pA=pB,即mv=2mvB,得碰前vB=v2,碰后v′A=v2,由动量守恒定律,有mv+2m×v2=m×v2+2mv′B,解得v′B=3v4,所以vA'∶v′B=v2∶3v4=23,D正确.
答案:D
考点突破
例1 解析:本题考查子弹打物块模型与弹簧的结合.子弹射入物块B的过程,由于时间极短,子弹与物块B组成的系统动量守恒,在此运动过程中,子弹的动能有一部分转化为系统的内能,则系统的机械能减小,所以系统的机械能不守恒,A错误;物块B和子弹一起向左运动的过程,系统受到墙壁的作用力,合外力不为零,则系统的动量不守恒,在此运动过程中,只有弹簧的弹力做功,所以系统的机械能守恒,B错误;弹簧推物块B向右运动,直到弹簧恢复原长的过程中,弹簧要恢复原长,墙壁对弹簧有向右的弹力,系统所受的合外力不为零,则系统的动量不守恒,在此运动过程中,只有弹簧的弹力做功,所以系统的机械能守恒,C错误;弹簧恢复原长后,物块A离开墙壁,物块B继续向右运动,系统所受的合外力为零,则系统的动量守恒,在此过程中只有弹簧的弹力做功,所以系统的机械能也守恒,D正确.
答案:D
例2 解析:由图象可知甲物块碰前速度v甲=5 m/s,乙物块碰前速度v乙=1 m/s,甲物块碰后速度v′甲=-1 m/s,乙物块碰后速度v′乙=2 m/s.甲和乙碰撞过程中系统动量守恒,有m甲v甲+m乙v乙=m甲v′甲+m乙v′乙,解得m乙=6 kg.碰撞过程中两物块损失的机械能
ΔE=12m甲v甲2+12 m乙v乙2-12m甲v甲′2-12m乙v乙′2=3 J.故选A项.
答案:A
例3 解析:当小球在槽内由A运动到B的过程中,左侧物块对槽有作用力,小球与槽组成的系统水平方向上的动量不守恒,故B错误;当小球由B运动到C的过程中,因小球对槽有斜向右下方的压力,槽做加速运动,动能增加,小球机械能减少,槽对小球的支持力对小球做了负功,故A错误;小球从B到C的过程中,系统水平方向所受合外力为零,满足系统水平方向动量守恒,故C正确;小球离开C点以后,既有竖直向上的分速度,又有水平分速度,小球做斜上抛运动,故D错误.
答案:C
例4 解析:由题意可知,A、B做自由落体运动,由v2=2gH,可得A、B的落地速度的大小v=2gH,A反弹后与B的碰撞为瞬时作用,A、B组成的系统在竖直方向上所受合力虽然不为零,但作用时间很短,系统的内力远大于外力,所以动量近似守恒,故有m1v-m2v=0+m2v′2,B上升高度h=v2'2 2g,联立并代入数据得h=4.05 m,A正确.
答案:A
练1 解析:物体与油泥粘合的过程,发生非弹性碰撞,系统机械能有损失,故A错误;整个系统在水平方向不受外力,竖直方向上合外力为零,则系统动量一直守恒,故B正确;取系统的初速度方向为正方向,根据动量守恒定律可知,物体在沿车滑动到B端粘在B端的油泥上后系统共同的速度与初速度是相同的,故C正确;由C的分析可知,当物体与B端油泥粘在一起时,系统的速度与初速度相等,所以系统的末动能与初动能是相等的,系统损失的机械能等于弹簧的弹性势能,与物体滑动中有没有摩擦无关,故D正确.
答案:BCD
练2 解析:物块每次与挡板碰撞后,挡板对物块的冲量I冲=mv0-m(-v0)=40 kg·m·s-1,方向与运动员退行方向相同,以此方向为正方向,以运动员和物块整体为研究对象,当物块撞击挡板7次后,7I冲=m人v7+mv0,v7<5 m/s,得m人>52 kg,当物块撞击挡板8次后,8I冲=m人v8+mv0,v8>5 m/s,得m人<60 kg.故B、C正确,A、D错误.
答案:BC
练3 解析:设小孩把车A总共推出n次后,车A返回时,小孩恰好不能再接到小车A.此时,车A返回时的速度v与车B的速度恰好相等,即vB=v①
第1次推车时,小孩和车B获得的动量为mAv,以后每次推车时获得的动量为2mAv,根据动量守恒定律得
mAv+(n-1)·2mAv=mBvB②
又由题意知4mA=mB③
联立①②③解得n=2.5,
所以小孩把车A总共推出3次后,车A返回时,小孩不能再接到小车A.
答案:3次
例5 解析:碰撞前总动量为p=mPvP0=4 kg·m/s,碰撞前总动能为Ek=12mPvP02=8 J.如果vP=vQ=43 m/s,p′=mPvP+mQvQ=4 kg·m/s,E′k=12mPvP2+12mQvQ2=83 J,碰撞过程动量守恒,能量不增加,A正确;如果vP=-1 m/s,vQ=2.5 m/s,p′=mPvP+mQvQ=4 kg·m/s,E′k=12mPvP2+12mQvQ2=6.75 J,能量不增加,碰撞过程动量守恒,B正确;如果vP=1 m/s,vQ=3 m/s,p′=mPvP+mQvQ=7 kg·m/s,碰撞过程动量不守恒,C错误;如果vP=-4 m/s,vQ=4 m/s,p′=mPvP+mQvQ=4 kg·m/s,E′k=12mPvP2+12mQvQ2=24 J,碰撞过程动量守恒,动能增加,D错误.
答案:AB
例6 解析:(1)设A、B在O点碰后的速度分别为v1和v2,以向右为正方向.由动量守恒定律得:mv0=mv1+Mv2.碰撞前后动能相等,则得:12mv02=12mv12+12Mv22,解得:v1=-2 m/s,方向向左,v2=4 m/s,方向向右.
(2)碰后,两物块在OQ段减速时加速度大小均为:a=μg=2 m/s2.B经过t1时间与Q处挡板相碰,由运动学公式:v2t1-12at12=d,得:t1=1 s(t1=3 s舍去).与挡板碰后,B的速度大小v3=v2-at1=2 m/s,反弹后减速时间t2=v3a=1 s,反弹后经过位移s1=v32 2a=1 m,B停止运动.物块A与P处挡板碰后,以v4=2 m/s的速度滑上O点,经过s2=v42 2a=1 m停止.所以最终A、B的距离s=d-s1-s2=1 m,两者不会碰第二次.在A、B碰后,A运动总时间tA=2L-dv1+v4a=3 s,B运动总时间 tB=t1+t2=2 s,则时间间隔ΔtAB=tA-tB=1 s.
答案:(1)2 m/s,方向向左 4 m/s,方向向右 (2)1 s
例7 解析:(1)设第一辆车碰前瞬间的速度为v1,碰前两车间距为L1,与第二辆车碰后的共同速度为v2,共同移动的距离为L2,由动量守恒定律有mv1=2mv2
由动能定理有-0.2×2mgL2=0-122mv22
则碰撞中系统损失的机械能ΔE=12mv12-122mv22
联立解得ΔE=40 J
(2)设第一辆车推出时的速度为v0
由动能定理有-0.2mgL1=12mv12-12mv02
第一辆车的水平冲量大小I=mv0
联立解得I=207 N·s
答案:(1)40 J (2)207 N·s
练4 解析:滑块A下滑过程,由机械能守恒定律得mAgR=12mAv02 ,解得v0=6 m/s.若两个滑块发生的是弹性碰撞,取向右为正方向,由动量守恒定律和机械能守恒定律得mAv0=mAvA+mBvB,12mAv02=12mAvA2+12mBvB2,解得vB=4 m/s.若两个滑块发生的是完全非弹性碰撞,由动量守恒定律得mAv0=(mA+mB)v′B,解得v′B=2 m/s.所以碰后小滑块B的速度范围为2 m/s≤vB≤4 m/s,不可能为5 m/s.
答案:A
练5 解析:设碰撞前羽毛球和羽毛球拍的速度分别为v1和v2,碰后羽毛球和羽毛球拍的速度分别为v′1和v′2.取碰撞前羽毛球的速度方向为正方向,根据动量守恒定律和机械能守恒定律得
m1v1+m2v2=m1v′1+m2v2′.①
12m1v12+12m2v22=12m1v1'2+12m2v2'2.②
联立解得v′1=m1-m2v1+2m2v2m1+m2
据题有m1?m2,
则得v′1=2v2-v1=[2×10-(-5)] m/s=25 m/s.
答案:A
例8 解析:本题考查反冲运动,打一次喷嚏大约喷出气体的质量m=ρV,由动量定理得FΔt=mv,解得F=mvΔt=ρVvΔt=1.3×50×10-6×400.02 N=0.13 N,根据牛顿第三定律可知,打一次喷嚏人受到的平均反冲力为0.13 N,故选B.
答案:B
例9 解析:本题考查“人船模型”.人与平板车组成的系统动量守恒,由动量守恒定律得mv人+Mv车=0,故平板车运动的方向一定与人运动的方向相反,故人与平板车的速度方向相反,人在车上向右行走时,车将向左运动,A错误;因人与平板车的总动量为零,故人停止走动,速度为零时,车的速度也为零,B错误;因人与车的运动时间相等,动量守恒,以人行走的方向为正方向,则mx人-Mx车=0,故车与人的位移之比为x车x人=mM,则车的位移与人的运动速度无关,不论人的速度多大,车在地面上移动的距离都相等,C错误,D正确.
答案:D
例10 解析:本题考查动能定理、动量守恒定律和能量守恒定律.(1)设滑块B返回水平面的速度大小为v′B,在斜面上运动的最大距离为L,则L=hsin37°,滑块B从斜面最高点返回水平面,由动能定理得(mBg sin 37°-μmBg cos 37°)L=12mBvB'2-0,联立解得v′B=2 m/s.
(2)设滑块B滑上斜面的初速度大小为vB,滑块B从水平面滑到斜面最高点,由动能定理得-(mBg sin 37°+μmBg cos 37°)L=0-12mBvB2,点燃炸药后,由动量守恒定律得mAvA-mBvB=0,由能量守恒定律得E=12mAvA2+12mBvB2,联立解得E=30 J.
(3)滑块A恰好到达半圆轨道的最高点,有mAg=mAvA'2 R,由动能定理得-2mAgR-Wf=12mAvA'2-12mAvA2,联立解得Wf=11 J.
答案:(1)2 m/s (2)30 J (3)11 J
练6 解析:本题考查爆炸中的动量守恒问题.爆竹在最高点速度大小为v0、方向水平向右,爆炸前动量为3mv0,其中一块质量为2m,速度大小为v,方向水平向右,设爆炸后另一块瞬时速度大小为v′,取爆竹到最高点未爆炸前的速度方向为正方向,爆炸过程动量守恒,则3mv0=2mv+mv′,解得v′=3v0-2v,C正确,A、B、D错误.
答案:C
练7 解析:本题考查动量守恒定律、机械能守恒定律.设当轻绳与横杆成直角时,圆环的速度为v1,根据圆环、小球组成的系统在水平方向动量守恒,则有2mv=mv1,由于机械能守恒,则有2mgl=12(2m)v2+12mv12,联立解得v=23gl,圆环、小球运动的时间相等,则有2m(l-x)=mx,解得x=23l,A正确,B、C、D错误.
答案:A
同课章节目录
