2020-2021学年 高一物理 运动的描述 强化学案Word版含答案
文档属性
| 名称 | 2020-2021学年 高一物理 运动的描述 强化学案Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-14 13:10:14 | ||
图片预览



文档简介
运动的描述
知识点一 质点和参考系
1.质点
(1)用来代替物体的有________的点叫做质点.
(2)研究一个物体的运动时,如果物体的________和________对所研究问题的影响可以忽略,就可以看做质点.
(3)质点是一种理想化模型,实际并不存在.
2.参考系
(1)参考系可以是运动的物体,也可以是________的物体,但被选为参考系的物体,我们都假定它是静止的.
(2)比较两物体的运动情况时,必须选同一________.
(3)选取不同的物体作为参考系,对同一物体运动的描述可能________.通常以________为参考系.
知识点二 位移和速度
1.位移和路程
位移
路程
定义
表示质点位置的变动,它是质点由______指向______的有向线段
等于质点________的长度
区别
(1)位移是______,方向由初位置指向末位置
(2)路程是标量,没有______
联系
(1)在单向直线运动中,位移的大小______路程
(2)其他情况下,位移的大小______路程
2.速度与速率
(1)平均速度:在变速运动中,物体发生的位移与发生这段位移所用时间的比值,即v=______,是矢量,其方向就是对应________的方向.
(2)瞬时速度:运动物体在某一时刻或经过某一________的速度,是矢量,其方向是物体的运动方向或沿运动轨迹的________方向.
(3)速率:________的大小,是标量.
(4)平均速率:物体运动实际________与发生这段路程所用________的比值,不一定等于平均速度的大小.
知识点三 加速度
1.物理意义:描述物体速度________和方向的物理量,是状态量.
2.定义式:a=△v△t=________.
3.决定因素:a不是由v、Δt、Δv决定,而是由Fm决定.
4.方向:与Δv的方向一致,由________的方向决定,而与v0、v的方向无关.
思考辨析
(1)研究花样游泳运动员的动作时,不能把运动员看成质点.( )
(2)参考系必须是静止的物体.( )
(3)做直线运动的物体的位移大小一定等于路程.( )
(4)平均速度的方向与位移的方向相同.( )
(5)子弹击中目标时的速度属于瞬时速度.( )
(6)速度变化率越大,加速度越大.( )
(7)加速度为正值,表示速度大小一定越来越大.( )
教材改编
[人教版必修1P29T2改编]
(多选)下列说法中可能正确的是( )
A.物体运动的加速度等于0,而速度却不等于0
B.两物体相比,一个物体的速度变化量比较大,其加速度一定较大
C.物体具有向东的加速度,而速度的方向却向西
D.物体做直线运动,后一阶段的加速度比前一阶段小,但速度却比前一阶段大
考点一 对质点、参考系、位移的理解
自主演练
1.三个概念的进一步理解
(1)质点不同于几何“点”,它无大小但有质量,能否看成质点是由研究问题的性质决定,而不是依据物体自身大小和形状来判断.
(2)参考系是为了研究物体的运动而假定不动的物体.
(3)位移是由初位置指向末位置的有向线段,线段的长度表示位移大小.
2.三点注意
(1)对于质点要从建立理想化模型的角度来理解.
(2)在研究两个物体间的相对运动时,选择其中一个物体为参考系,可以使分析和计算更简单.
(3)位移的矢量性是研究问题时应切记的性质.
[多维练透]
1.(多选)如图所示是一架正在进行航拍的四旋翼无人飞机.则下列有关无人机运动情况的说法正确的是( )
A.调整无人机在空中飞行的姿态时可将其看成质点
B.观察无人机的飞行轨迹时不能将其看成质点
C.地面观察者观察无人机在空中的位置时可将其看成质点
D.地面上的人看到无人机从头顶飞过,是以地面为参考系
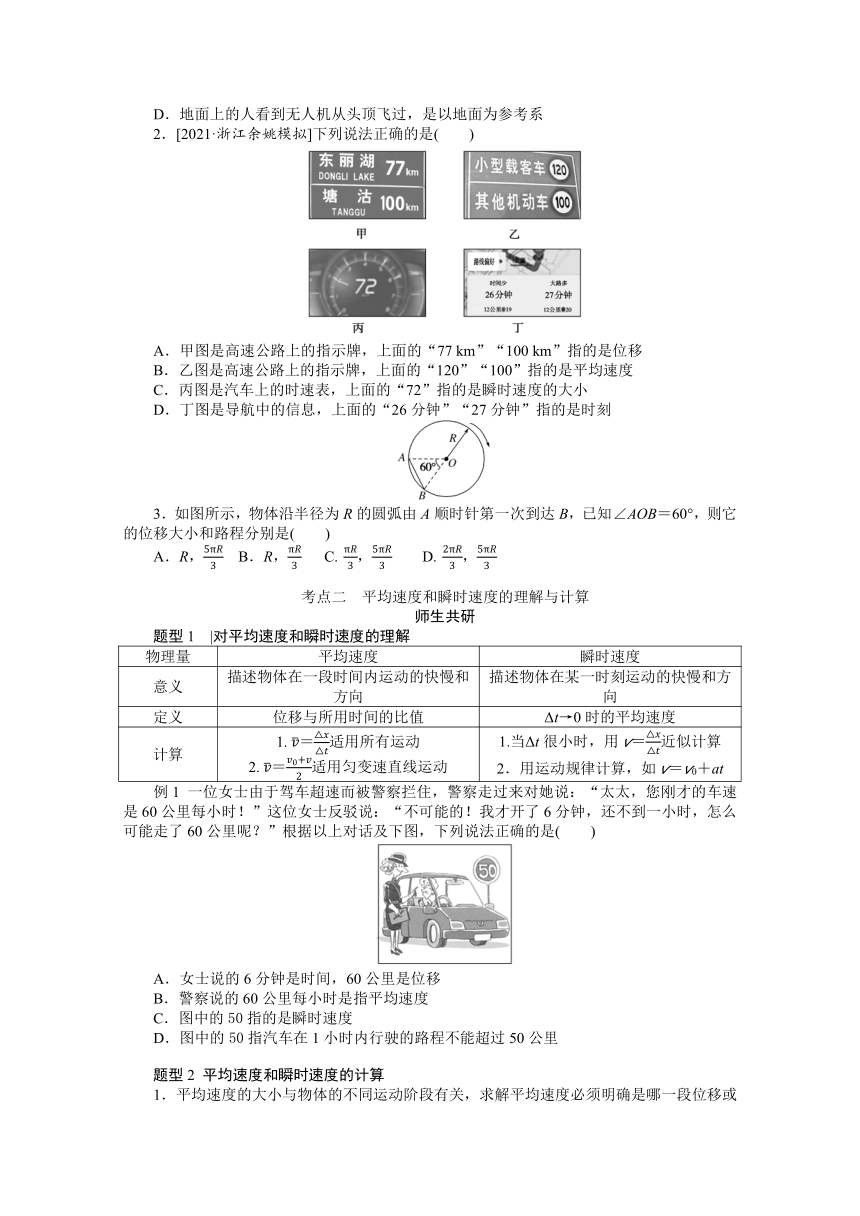
2.[2021·浙江余姚模拟]下列说法正确的是( )
A.甲图是高速公路上的指示牌,上面的“77 km”“100 km”指的是位移
B.乙图是高速公路上的指示牌,上面的“120”“100”指的是平均速度
C.丙图是汽车上的时速表,上面的“72”指的是瞬时速度的大小
D.丁图是导航中的信息,上面的“26分钟”“27分钟”指的是时刻
3.如图所示,物体沿半径为R的圆弧由A顺时针第一次到达B,已知∠AOB=60°,则它的位移大小和路程分别是( )
A.R,5πR3 B.R,πR3 C. πR3,5πR3 D. 2πR3,5πR3
考点二 平均速度和瞬时速度的理解与计算
师生共研
题型1 |对平均速度和瞬时速度的理解
物理量
平均速度
瞬时速度
意义
描述物体在一段时间内运动的快慢和方向
描述物体在某一时刻运动的快慢和方向
定义
位移与所用时间的比值
Δt→0时的平均速度
计算
1. v=△x△t适用所有运动
2. v=v0+v2适用匀变速直线运动
1.当Δt很小时,用v=△x△t近似计算
2.用运动规律计算,如v=v0+at
例1 一位女士由于驾车超速而被警察拦住,警察走过来对她说:“太太,您刚才的车速是60公里每小时!”这位女士反驳说:“不可能的!我才开了6分钟,还不到一小时,怎么可能走了60公里呢?”根据以上对话及下图,下列说法正确的是( )
A.女士说的6分钟是时间,60公里是位移
B.警察说的60公里每小时是指平均速度
C.图中的50指的是瞬时速度
D.图中的50指汽车在1小时内行驶的路程不能超过50公里
题型2 平均速度和瞬时速度的计算
1.平均速度的大小与物体的不同运动阶段有关,求解平均速度必须明确是哪一段位移或哪一段时间内的平均速度.
2. v=△x△t是平均速度的定义式,适用于所有的运动.
3.用极短时间内的平均速度来表示某时刻的瞬时速度.
例2 如图所示,物体沿曲线轨迹的箭头方向运动,AB、ABC、ABCD、ABCDE四段曲线轨迹运动所用的时间分别是:1 s、2 s、3 s、4 s.下列说法错误的是( )
A.物体在AB段的平均速度为1 m/s
B.物体在ABC段的平均速度为52 m/s
C.AB段的平均速度比ABC段的平均速度更能反映物体处于A点时的瞬时速度
D.物体在B点的速度等于AC段的平均速度
练1 在土耳其伊斯坦布尔举行的第15届机器人世界杯赛上,中国科技大学的“蓝鹰”队获得仿真2D组冠军和服务机器人组亚军,改写了我国服务机器人从未进入世界前5的历史,标志着我国在该领域的研究取得了重要进展.图中是科大著名服务机器人“可佳”,如图所示,现要执行一项任务,给它设定了如下动作程序:机器人在平面内由点(1,1)出发,沿直线运动到点(4,2),然后又由点(4,2)沿直线运动到点(2,5),然后又由点(2,5)沿直线运动到点(6,6),然后又由点(6,6)沿直线运动到点(3,3).整个过程中机器人所用时间是22 s,则( )
A.机器人的运动轨迹是一条直线
B.整个过程中机器人的位移大小为22 m
C.机器人不会两次通过同一点
D.整个过程中机器人的平均速度为1.5 m/s
练2 (多选)如图所示,一人骑自行车晨练,由静止开始沿直线运动,她在第1 s内、第2 s内、第3 s内、第4 s内通过的位移分别为1 m、2 m、3 m、4 m,则( )
A.她在4 s末的瞬时速度大小为4 m/s
B.她在第2 s内的平均速度大小为2 m/s
C.她在4 s内的平均速度大小为2.5 m/s
D.她在1 s末的瞬时速度大小为1 m/s
考点三 加速度的理解与计算
多维探究
题型1|速度、速度变化量和加速度的关系
1.三者无必然联系,v很大,Δv可能很小,甚至为0,a也可很大或很小.
2.加速度的决定式是a=Fm,即加速度的大小由物体受到的合力F和物体的质量m共同决定,加速度的方向由合力的方向决定.
例3 有下列几种情形,正确的是( )
A.点火后即将升空的火箭,因为火箭还没运动,所以加速度一定为零
B.高速公路上沿直线高速行驶的轿车为避免事故紧急刹车,因紧急刹车,速度变化很快,所以加速度很大
C.高速行驶的磁悬浮列车,因速度很大,所以加速度一定很大
D.100米比赛中,甲比乙跑得快,说明甲的加速度大于乙的加速度
题型2|加速度的计算
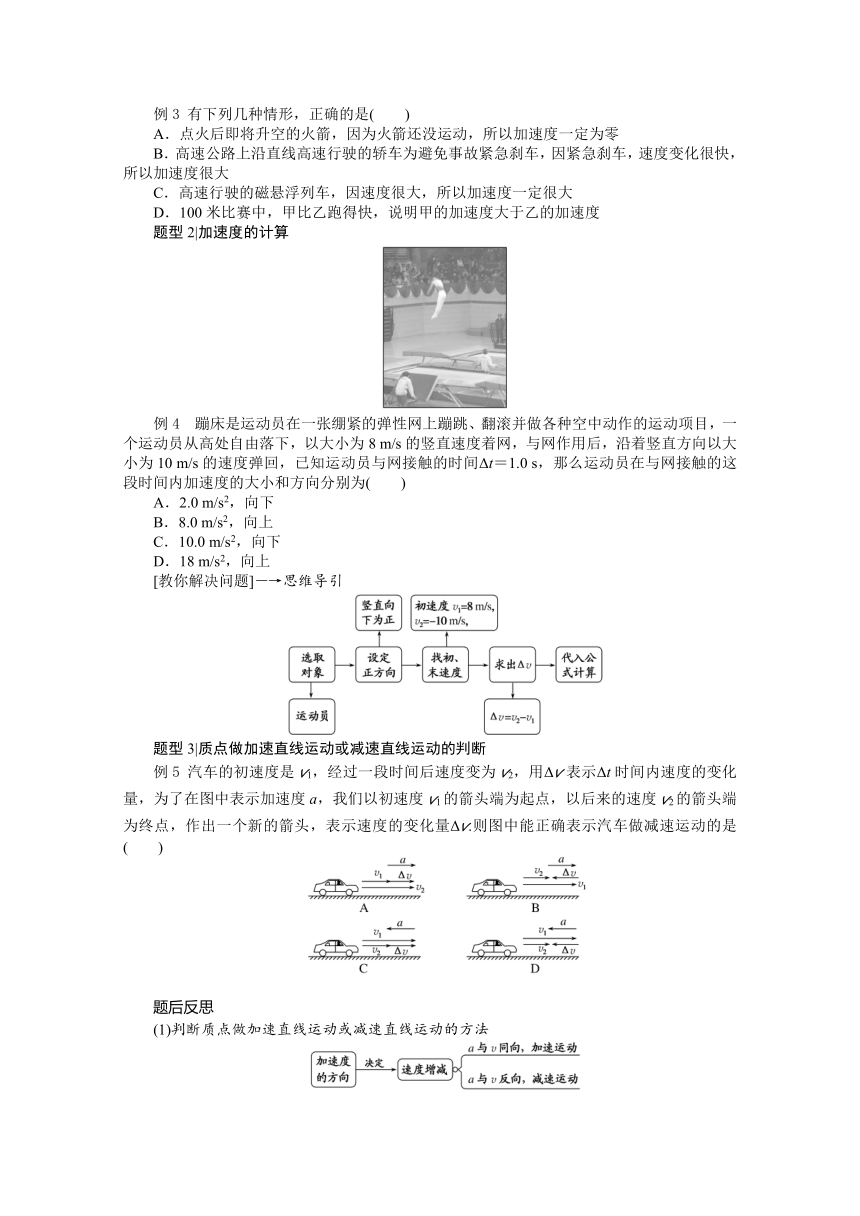
例4 蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目,一个运动员从高处自由落下,以大小为8 m/s的竖直速度着网,与网作用后,沿着竖直方向以大小为10 m/s的速度弹回,已知运动员与网接触的时间Δt=1.0 s,那么运动员在与网接触的这段时间内加速度的大小和方向分别为( )
A.2.0 m/s2,向下
B.8.0 m/s2,向上
C.10.0 m/s2,向下
D.18 m/s2,向上
[教你解决问题]―→思维导引
题型3|质点做加速直线运动或减速直线运动的判断
例5 汽车的初速度是v1,经过一段时间后速度变为v2,用Δv表示Δt时间内速度的变化量,为了在图中表示加速度a,我们以初速度v1的箭头端为起点,以后来的速度v2的箭头端为终点,作出一个新的箭头,表示速度的变化量Δv.则图中能正确表示汽车做减速运动的是( )
题后反思
(1)判断质点做加速直线运动或减速直线运动的方法
(2)计算加速度的方法:
(3)加速度的“+”“-”只表示加速度的方向,不表示大小.练3 物体A的加速度为3 m/s2,物体B的加速度为-5 m/s2,下列说法中,正确的是( )
A.物体A的加速度比物体B的加速度大
B.物体B的速度变化比物体A的速度变化快
C.物体A的速度一定在增加
D.物体B的速度一定在减小
练4 (多选)如图所示,物体以5 m/s的初速度沿光滑的斜面向上做减速运动,经过2 s速度大小变为3 m/s,则物体的加速度( )
A.大小为1 m/s2,方向沿斜面向上
B.大小为1 m/s2,方向沿斜面向下
C.大小为4 m/s2,方向沿斜面向下
D.大小为4 m/s2,方向沿斜面向上
思维拓展
测量速度的三种方法
方法1 利用光电计时器测速度
典例1 利用如图所示的装置测量滑块P的速度.1和2是固定在斜面上适当位置的两个光电门,当有物体从光电门通过时,与它们连接的光电计时器能够显示挡光时间.让滑块从斜面的顶端滑下,光电门1、2各自连接的光电计时器显示的挡光时间分别为5.00×10-2 s、2.00×10-2 s.已知滑块的宽度为5.00 cm(结果保留两位有效数字),求:
(1)滑块通过光电门1、2时的速度分别是v1=________ m/s,v2=________ m/s.
(2)若用宽度是2.00 cm的滑块,对测量误差有何影响?
________________________________________________________________________
方法提炼
根据v=△x△t,当时间很短时,平均速度可近似等于瞬时速度.本方法是将物体通过光电门时的平均速度近似等于物体通过1、2位置时的瞬时速度.
方法2 利用打点计时器测速度
典例2 某同学在“用打点计时器测速度”的实验中,使用的是照明电路中“220 V 50 Hz”的交流电,纸带做匀变速直线运动,记录的纸带如图所示,在纸带上确定出A、B、C、D、E、F、G共7个计数点.每两个相邻的测量点之间还有4个点未画出.
(1)根据数据计算出B和F点的瞬时速度,vB=________ m/s,vF=________ m/s(结果要求保留两位有效数字).
(2)如果交变电流的频率是f=49 Hz,而做实验的同学并不知道,那么速度的测量值与实际值相比________(填“偏大”“偏小”或“不变”).
方法提炼
根据匀变速直线运动中,某段时间内中间时刻的瞬时速度等于这段时间的平均速度,计算瞬时速度.题目中强调纸带的运动为匀变速直线运动,恰好符合这个规律.
方法3 利用超声波测车速
典例3 如图是在高速公路上用超声波测速仪测量车速的示意图,测速仪发出并接收超声波脉冲信号,根据发出和接收到的信号间的时间差,测出被测物体的速度.现测速仪对距其x=380 m的匀速行驶中的汽车发出超声波信号,超声波信号从发出到被反射回来的时间间隔Δt=2.0 s,超声波在空气中传播的速度是v声=340 m/s,则当测速仪接收到被反射回来的超声波信号时,汽车前进的距离为( )
A.100 m B.60 m C.80 m D.120 m
练1 小明同学在学习了DIS实验后,设计了一个测物体瞬时速度的实验,其装置如图所示.在小车上固定挡光片,使挡光片的前端与车头齐平,将光电门传感器固定在轨道侧面,垫高轨道的一端.小明同学将小车从该端同一位置由静止释放,获得了如下几组实验数据.
实验次数
不同的挡光片
通过光电门的时间(s)
速度(m/s)
第一次
Ⅰ
0.230 44
0.347
第二次
Ⅱ
0.174 64
0.344
第三次
Ⅲ
0.116 62
0.343
第四次
Ⅳ
0.058 50
0.342
则以下表述正确的是( )
A.四个挡光片中,挡光片Ⅰ的宽度最小
B.四个挡光片中,挡光片Ⅲ的宽度最小
C.四次实验中,第一次实验测得的速度最接近小车车头到达光电门时的瞬时速度
D.四次实验中,第四次实验测得的速度最接近小车车头到达光电门时的瞬时速度
练2 [2021·大连模拟]一辆客车在某高速公路上行驶,在经过某直线路段时,司机驾车做匀速直线运动。司机发现其将要通过正前方高山悬崖下的隧道,于是鸣笛,5 s后听到回声,听到回声后又行驶10 s司机第二次鸣笛,3 s后听到回声.已知此高速公路的最高限速为120 km/h,声音在空气中的传播速度为340 m/s.请根据以上数据帮助司机计算一下客车的速度,看客车是否超速行驶,以便提醒司机安全行驶.
第1讲 运动的描述
基础落实
知识点一
1.(1)质量 (2)形状 大小
2.(1)静止 (2)参考系 (3)不同 地球
知识点二
1.初位置 末位置 运动轨迹 矢量 方向 等于 小于
2.(1) △x△t 位移 (2)位置 切线
(3)瞬时速度 (4)路程 时间
知识点三
1.变化快慢
2. v-v0△t
4.合外力
思考辨析
(1)√ (2)× (3)× (4)√ (5)√ (6)√ (7)×
教材改编
解析:根据加速度的定义式a=△v△t可知,速度改变量Δv越大,若需要的时间更长,则加速度可能较小,故B错误,A、C、D都对.
答案:ACD
考点突破
1.解析:调整无人机在空中飞行的姿态时,飞机的大小和形状不能忽略不计,不能看作质点,A项错误;观察飞机在空中的位置和飞行轨迹时,飞机的大小和形状是次要因素,可将其看成质点,B项错误,C项正确;地面上的人看到无人机从头顶飞过,是以地面为参考系,D项正确.
答案:CD
2.解析:本题考查生活实际中位移与路程、平均速度与瞬时速度、时间与时刻概念的辨识.甲图是高速公路上的指示牌,上面的“77 km”“100 km”指的是路程,故A错误;乙图是高速公路上的指示牌,上面的“120”“100”指的是瞬时速度的大小,故B错误;丙图是汽车上的时速表,上面的“72”指的是瞬时速度的大小,故C正确;丁图是导航中的信息,上面的“26分钟”“27分钟”指的是时间间隔,故D错误.
答案:C
3.解析:物体沿半径为R的圆弧由A顺时针第一次到达B,已知∠AOB=60°,则它转过的角度为300°,为56个圆周;位移是从初位置指向末位置的有向线段,故位移大小等于半径R;路程为圆的周长的56,即为53πR,故A项正确,B、C、D三项错误.
答案:A
例1 解析:50指瞬时速度不能超过50 km/h,其他选项均错误.
答案:C
例2 解析:由v=△x△t可得vAB=11 m/s=1 m/s,vAC=52m/s,故A、B均正确;所选取的过程离A点越近,其阶段的平均速度越接近A点的瞬时速度,故C正确;由A经B到C的过程不是匀变速直线运动过程,故B点虽为中间时刻,但其速度不等于AC段的平均速度,D错误.
答案:D
练1 解析:根据坐标分析可知轨迹为曲线,A项错误;位移为从(1,1)点到(3,3)点的有向线段,总位移为22 m,B项正确;机器人会两次通过同一点,C项错误;整个过程中平均速度v=xt=2222 m/s=1 m/s,D项错误.
答案:B
练2 解析:由v=△x△t可得该人在第2 s内的平均速度为2 m/s,B项正确;前4 s内的平均速度为v=1+2+3+44 m/s=2.5 m/s,C项正确;因该人的运动不是匀变速直线运动,故无法确定其瞬时速度大小,A、D项均错误.
答案:BC
例3 解析:点火后即将升空的火箭,火箭还没运动,但由于合外力不为零,加速度不为零,选项A错误;轿车紧急刹车,速度变化很快,根据加速度的定义式a=△v△t可知,加速度很大,选项B正确;高速行驶的磁悬浮列车,速度很大,但速度变化较小,加速度很小,选项C错误;100米比赛中,甲比乙跑得快,说明甲的速度大于乙的速度,选项D错误.
答案:B
例4 解析:方法一:取初速度的方向为正方向,即取着网前的速度方向为正方向,则v1=8 m/s,v2=-10 m/s,则a=v2-v1△t=-10-81.0 m/s2=-18 m/s2,负号说明加速度的方向与正方向相反,即向上,选项D正确.
方法二:取末速度的方向为正方向,即着网后的速度方向为正方向,则v1=-8 m/s,v2=10 m/s,则a=v2-v1△t=10+81.0 m/s2=18 m/s2,说明加速度的方向与正方向相同,选项D正确.
答案:D
例5 解析:速度变化量的方向与加速度方向一致,加速度方向与初速度方向相同时汽车做加速运动,加速度方向与初速度方向相反时汽车做减速运动.选项A中汽车做加速运动,选项B、C中分别是a的方向、Δv的方向作错了,选项D中图示能正确表示汽车做减速运动.故本题应选D.
答案:D
练3 解析:物体B的加速度大于物体A的加速度,可知物体B的速度变化比较快,故A错误,B正确.由于物体A、B的加速度方向与速度方向的关系未知,则无法判断物体A、B的速度是增加还是减小,故C、D错误.
答案:B
练4 解析:取初速度方向为正方向,则v0=5 m/s.若2 s后的速度方向沿斜面向上,v=3 m/s,则a=△v△t=v-v0△t=3-52 m/s2=-1 m/s2,即加速度大小为1 m/s2,方向沿斜面向下;若2 s后的速度方向沿斜面向下,v=-3 m/s,则a=△v△t=v-v0△t=-3-52 m/s2=-4 m/s2,即加速度大小为4 m/s2,方向沿斜面向下.故选项A、D错误,B、C正确.
答案:BC
思维拓展
典例1
解析:(1)v1=dΔt1=5×10-2m5×10-2s=1.0 m/s
v2=dΔt2=5×10-2m5×10-2s=2.5 m/s
(2)滑块宽度越小,挡光时间越短,平均速度越接近瞬时速度,误差越小.
答案:(1)1.0 2.5 (2)见解析
典例2 解析:(1)vB=AC2T=3.62+4.382×0.1×10-2 m/s=0.40 m/s
vF=EG2T=6.80+7.602×0.1×10-2 m/s=0.72 m/s
(2)计算时使用的频率偏大,时间间隔偏小,则测量的速度值偏大.
答案:(1)0.40 0.72 (2)偏大
典例3 解析:超声波信号从发出到被反射回来的时间间隔Δt=2.0 s,在1.0 s内,超声波前进距离为:x1=v声·12Δt=340×1 m=340 m;故汽车速度为:v=380-3401m/s=40 m/s;当测速仪接收到被反射回来的超声波信号时,汽车前进了:Δx=40×2 m=80 m,故C项正确.
答案:C
练1 解析:由题表知,四次实验的速度大小接近,挡光片的速度v=xt,计算可知Ⅳ的宽度最小,第四次实验测得的速度最接近小车车头到达光电门时的瞬时速度,D项正确.
答案:D
练2 解析:客车行驶示意图如图所示,设客车行驶速度为v1,声速为v2,客车第一次鸣笛时与悬崖距离为L,由题意有2L-v1×5 s=v2×5 s.
当客车第二次鸣笛时,客车距悬崖为L′,
则2L′-v1×3 s=v2×3 s.
又L′=L-v1×15 s,由以上各式,
解得v1=v214≈24.3 m/s=87.48 km/h<120 km/h.
故客车未超速.
答案:未超速
知识点一 质点和参考系
1.质点
(1)用来代替物体的有________的点叫做质点.
(2)研究一个物体的运动时,如果物体的________和________对所研究问题的影响可以忽略,就可以看做质点.
(3)质点是一种理想化模型,实际并不存在.
2.参考系
(1)参考系可以是运动的物体,也可以是________的物体,但被选为参考系的物体,我们都假定它是静止的.
(2)比较两物体的运动情况时,必须选同一________.
(3)选取不同的物体作为参考系,对同一物体运动的描述可能________.通常以________为参考系.
知识点二 位移和速度
1.位移和路程
位移
路程
定义
表示质点位置的变动,它是质点由______指向______的有向线段
等于质点________的长度
区别
(1)位移是______,方向由初位置指向末位置
(2)路程是标量,没有______
联系
(1)在单向直线运动中,位移的大小______路程
(2)其他情况下,位移的大小______路程
2.速度与速率
(1)平均速度:在变速运动中,物体发生的位移与发生这段位移所用时间的比值,即v=______,是矢量,其方向就是对应________的方向.
(2)瞬时速度:运动物体在某一时刻或经过某一________的速度,是矢量,其方向是物体的运动方向或沿运动轨迹的________方向.
(3)速率:________的大小,是标量.
(4)平均速率:物体运动实际________与发生这段路程所用________的比值,不一定等于平均速度的大小.
知识点三 加速度
1.物理意义:描述物体速度________和方向的物理量,是状态量.
2.定义式:a=△v△t=________.
3.决定因素:a不是由v、Δt、Δv决定,而是由Fm决定.
4.方向:与Δv的方向一致,由________的方向决定,而与v0、v的方向无关.
思考辨析
(1)研究花样游泳运动员的动作时,不能把运动员看成质点.( )
(2)参考系必须是静止的物体.( )
(3)做直线运动的物体的位移大小一定等于路程.( )
(4)平均速度的方向与位移的方向相同.( )
(5)子弹击中目标时的速度属于瞬时速度.( )
(6)速度变化率越大,加速度越大.( )
(7)加速度为正值,表示速度大小一定越来越大.( )
教材改编
[人教版必修1P29T2改编]
(多选)下列说法中可能正确的是( )
A.物体运动的加速度等于0,而速度却不等于0
B.两物体相比,一个物体的速度变化量比较大,其加速度一定较大
C.物体具有向东的加速度,而速度的方向却向西
D.物体做直线运动,后一阶段的加速度比前一阶段小,但速度却比前一阶段大
考点一 对质点、参考系、位移的理解
自主演练
1.三个概念的进一步理解
(1)质点不同于几何“点”,它无大小但有质量,能否看成质点是由研究问题的性质决定,而不是依据物体自身大小和形状来判断.
(2)参考系是为了研究物体的运动而假定不动的物体.
(3)位移是由初位置指向末位置的有向线段,线段的长度表示位移大小.
2.三点注意
(1)对于质点要从建立理想化模型的角度来理解.
(2)在研究两个物体间的相对运动时,选择其中一个物体为参考系,可以使分析和计算更简单.
(3)位移的矢量性是研究问题时应切记的性质.
[多维练透]
1.(多选)如图所示是一架正在进行航拍的四旋翼无人飞机.则下列有关无人机运动情况的说法正确的是( )
A.调整无人机在空中飞行的姿态时可将其看成质点
B.观察无人机的飞行轨迹时不能将其看成质点
C.地面观察者观察无人机在空中的位置时可将其看成质点
D.地面上的人看到无人机从头顶飞过,是以地面为参考系
2.[2021·浙江余姚模拟]下列说法正确的是( )
A.甲图是高速公路上的指示牌,上面的“77 km”“100 km”指的是位移
B.乙图是高速公路上的指示牌,上面的“120”“100”指的是平均速度
C.丙图是汽车上的时速表,上面的“72”指的是瞬时速度的大小
D.丁图是导航中的信息,上面的“26分钟”“27分钟”指的是时刻
3.如图所示,物体沿半径为R的圆弧由A顺时针第一次到达B,已知∠AOB=60°,则它的位移大小和路程分别是( )
A.R,5πR3 B.R,πR3 C. πR3,5πR3 D. 2πR3,5πR3
考点二 平均速度和瞬时速度的理解与计算
师生共研
题型1 |对平均速度和瞬时速度的理解
物理量
平均速度
瞬时速度
意义
描述物体在一段时间内运动的快慢和方向
描述物体在某一时刻运动的快慢和方向
定义
位移与所用时间的比值
Δt→0时的平均速度
计算
1. v=△x△t适用所有运动
2. v=v0+v2适用匀变速直线运动
1.当Δt很小时,用v=△x△t近似计算
2.用运动规律计算,如v=v0+at
例1 一位女士由于驾车超速而被警察拦住,警察走过来对她说:“太太,您刚才的车速是60公里每小时!”这位女士反驳说:“不可能的!我才开了6分钟,还不到一小时,怎么可能走了60公里呢?”根据以上对话及下图,下列说法正确的是( )
A.女士说的6分钟是时间,60公里是位移
B.警察说的60公里每小时是指平均速度
C.图中的50指的是瞬时速度
D.图中的50指汽车在1小时内行驶的路程不能超过50公里
题型2 平均速度和瞬时速度的计算
1.平均速度的大小与物体的不同运动阶段有关,求解平均速度必须明确是哪一段位移或哪一段时间内的平均速度.
2. v=△x△t是平均速度的定义式,适用于所有的运动.
3.用极短时间内的平均速度来表示某时刻的瞬时速度.
例2 如图所示,物体沿曲线轨迹的箭头方向运动,AB、ABC、ABCD、ABCDE四段曲线轨迹运动所用的时间分别是:1 s、2 s、3 s、4 s.下列说法错误的是( )
A.物体在AB段的平均速度为1 m/s
B.物体在ABC段的平均速度为52 m/s
C.AB段的平均速度比ABC段的平均速度更能反映物体处于A点时的瞬时速度
D.物体在B点的速度等于AC段的平均速度
练1 在土耳其伊斯坦布尔举行的第15届机器人世界杯赛上,中国科技大学的“蓝鹰”队获得仿真2D组冠军和服务机器人组亚军,改写了我国服务机器人从未进入世界前5的历史,标志着我国在该领域的研究取得了重要进展.图中是科大著名服务机器人“可佳”,如图所示,现要执行一项任务,给它设定了如下动作程序:机器人在平面内由点(1,1)出发,沿直线运动到点(4,2),然后又由点(4,2)沿直线运动到点(2,5),然后又由点(2,5)沿直线运动到点(6,6),然后又由点(6,6)沿直线运动到点(3,3).整个过程中机器人所用时间是22 s,则( )
A.机器人的运动轨迹是一条直线
B.整个过程中机器人的位移大小为22 m
C.机器人不会两次通过同一点
D.整个过程中机器人的平均速度为1.5 m/s
练2 (多选)如图所示,一人骑自行车晨练,由静止开始沿直线运动,她在第1 s内、第2 s内、第3 s内、第4 s内通过的位移分别为1 m、2 m、3 m、4 m,则( )
A.她在4 s末的瞬时速度大小为4 m/s
B.她在第2 s内的平均速度大小为2 m/s
C.她在4 s内的平均速度大小为2.5 m/s
D.她在1 s末的瞬时速度大小为1 m/s
考点三 加速度的理解与计算
多维探究
题型1|速度、速度变化量和加速度的关系
1.三者无必然联系,v很大,Δv可能很小,甚至为0,a也可很大或很小.
2.加速度的决定式是a=Fm,即加速度的大小由物体受到的合力F和物体的质量m共同决定,加速度的方向由合力的方向决定.
例3 有下列几种情形,正确的是( )
A.点火后即将升空的火箭,因为火箭还没运动,所以加速度一定为零
B.高速公路上沿直线高速行驶的轿车为避免事故紧急刹车,因紧急刹车,速度变化很快,所以加速度很大
C.高速行驶的磁悬浮列车,因速度很大,所以加速度一定很大
D.100米比赛中,甲比乙跑得快,说明甲的加速度大于乙的加速度
题型2|加速度的计算
例4 蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目,一个运动员从高处自由落下,以大小为8 m/s的竖直速度着网,与网作用后,沿着竖直方向以大小为10 m/s的速度弹回,已知运动员与网接触的时间Δt=1.0 s,那么运动员在与网接触的这段时间内加速度的大小和方向分别为( )
A.2.0 m/s2,向下
B.8.0 m/s2,向上
C.10.0 m/s2,向下
D.18 m/s2,向上
[教你解决问题]―→思维导引
题型3|质点做加速直线运动或减速直线运动的判断
例5 汽车的初速度是v1,经过一段时间后速度变为v2,用Δv表示Δt时间内速度的变化量,为了在图中表示加速度a,我们以初速度v1的箭头端为起点,以后来的速度v2的箭头端为终点,作出一个新的箭头,表示速度的变化量Δv.则图中能正确表示汽车做减速运动的是( )
题后反思
(1)判断质点做加速直线运动或减速直线运动的方法
(2)计算加速度的方法:
(3)加速度的“+”“-”只表示加速度的方向,不表示大小.练3 物体A的加速度为3 m/s2,物体B的加速度为-5 m/s2,下列说法中,正确的是( )
A.物体A的加速度比物体B的加速度大
B.物体B的速度变化比物体A的速度变化快
C.物体A的速度一定在增加
D.物体B的速度一定在减小
练4 (多选)如图所示,物体以5 m/s的初速度沿光滑的斜面向上做减速运动,经过2 s速度大小变为3 m/s,则物体的加速度( )
A.大小为1 m/s2,方向沿斜面向上
B.大小为1 m/s2,方向沿斜面向下
C.大小为4 m/s2,方向沿斜面向下
D.大小为4 m/s2,方向沿斜面向上
思维拓展
测量速度的三种方法
方法1 利用光电计时器测速度
典例1 利用如图所示的装置测量滑块P的速度.1和2是固定在斜面上适当位置的两个光电门,当有物体从光电门通过时,与它们连接的光电计时器能够显示挡光时间.让滑块从斜面的顶端滑下,光电门1、2各自连接的光电计时器显示的挡光时间分别为5.00×10-2 s、2.00×10-2 s.已知滑块的宽度为5.00 cm(结果保留两位有效数字),求:
(1)滑块通过光电门1、2时的速度分别是v1=________ m/s,v2=________ m/s.
(2)若用宽度是2.00 cm的滑块,对测量误差有何影响?
________________________________________________________________________
方法提炼
根据v=△x△t,当时间很短时,平均速度可近似等于瞬时速度.本方法是将物体通过光电门时的平均速度近似等于物体通过1、2位置时的瞬时速度.
方法2 利用打点计时器测速度
典例2 某同学在“用打点计时器测速度”的实验中,使用的是照明电路中“220 V 50 Hz”的交流电,纸带做匀变速直线运动,记录的纸带如图所示,在纸带上确定出A、B、C、D、E、F、G共7个计数点.每两个相邻的测量点之间还有4个点未画出.
(1)根据数据计算出B和F点的瞬时速度,vB=________ m/s,vF=________ m/s(结果要求保留两位有效数字).
(2)如果交变电流的频率是f=49 Hz,而做实验的同学并不知道,那么速度的测量值与实际值相比________(填“偏大”“偏小”或“不变”).
方法提炼
根据匀变速直线运动中,某段时间内中间时刻的瞬时速度等于这段时间的平均速度,计算瞬时速度.题目中强调纸带的运动为匀变速直线运动,恰好符合这个规律.
方法3 利用超声波测车速
典例3 如图是在高速公路上用超声波测速仪测量车速的示意图,测速仪发出并接收超声波脉冲信号,根据发出和接收到的信号间的时间差,测出被测物体的速度.现测速仪对距其x=380 m的匀速行驶中的汽车发出超声波信号,超声波信号从发出到被反射回来的时间间隔Δt=2.0 s,超声波在空气中传播的速度是v声=340 m/s,则当测速仪接收到被反射回来的超声波信号时,汽车前进的距离为( )
A.100 m B.60 m C.80 m D.120 m
练1 小明同学在学习了DIS实验后,设计了一个测物体瞬时速度的实验,其装置如图所示.在小车上固定挡光片,使挡光片的前端与车头齐平,将光电门传感器固定在轨道侧面,垫高轨道的一端.小明同学将小车从该端同一位置由静止释放,获得了如下几组实验数据.
实验次数
不同的挡光片
通过光电门的时间(s)
速度(m/s)
第一次
Ⅰ
0.230 44
0.347
第二次
Ⅱ
0.174 64
0.344
第三次
Ⅲ
0.116 62
0.343
第四次
Ⅳ
0.058 50
0.342
则以下表述正确的是( )
A.四个挡光片中,挡光片Ⅰ的宽度最小
B.四个挡光片中,挡光片Ⅲ的宽度最小
C.四次实验中,第一次实验测得的速度最接近小车车头到达光电门时的瞬时速度
D.四次实验中,第四次实验测得的速度最接近小车车头到达光电门时的瞬时速度
练2 [2021·大连模拟]一辆客车在某高速公路上行驶,在经过某直线路段时,司机驾车做匀速直线运动。司机发现其将要通过正前方高山悬崖下的隧道,于是鸣笛,5 s后听到回声,听到回声后又行驶10 s司机第二次鸣笛,3 s后听到回声.已知此高速公路的最高限速为120 km/h,声音在空气中的传播速度为340 m/s.请根据以上数据帮助司机计算一下客车的速度,看客车是否超速行驶,以便提醒司机安全行驶.
第1讲 运动的描述
基础落实
知识点一
1.(1)质量 (2)形状 大小
2.(1)静止 (2)参考系 (3)不同 地球
知识点二
1.初位置 末位置 运动轨迹 矢量 方向 等于 小于
2.(1) △x△t 位移 (2)位置 切线
(3)瞬时速度 (4)路程 时间
知识点三
1.变化快慢
2. v-v0△t
4.合外力
思考辨析
(1)√ (2)× (3)× (4)√ (5)√ (6)√ (7)×
教材改编
解析:根据加速度的定义式a=△v△t可知,速度改变量Δv越大,若需要的时间更长,则加速度可能较小,故B错误,A、C、D都对.
答案:ACD
考点突破
1.解析:调整无人机在空中飞行的姿态时,飞机的大小和形状不能忽略不计,不能看作质点,A项错误;观察飞机在空中的位置和飞行轨迹时,飞机的大小和形状是次要因素,可将其看成质点,B项错误,C项正确;地面上的人看到无人机从头顶飞过,是以地面为参考系,D项正确.
答案:CD
2.解析:本题考查生活实际中位移与路程、平均速度与瞬时速度、时间与时刻概念的辨识.甲图是高速公路上的指示牌,上面的“77 km”“100 km”指的是路程,故A错误;乙图是高速公路上的指示牌,上面的“120”“100”指的是瞬时速度的大小,故B错误;丙图是汽车上的时速表,上面的“72”指的是瞬时速度的大小,故C正确;丁图是导航中的信息,上面的“26分钟”“27分钟”指的是时间间隔,故D错误.
答案:C
3.解析:物体沿半径为R的圆弧由A顺时针第一次到达B,已知∠AOB=60°,则它转过的角度为300°,为56个圆周;位移是从初位置指向末位置的有向线段,故位移大小等于半径R;路程为圆的周长的56,即为53πR,故A项正确,B、C、D三项错误.
答案:A
例1 解析:50指瞬时速度不能超过50 km/h,其他选项均错误.
答案:C
例2 解析:由v=△x△t可得vAB=11 m/s=1 m/s,vAC=52m/s,故A、B均正确;所选取的过程离A点越近,其阶段的平均速度越接近A点的瞬时速度,故C正确;由A经B到C的过程不是匀变速直线运动过程,故B点虽为中间时刻,但其速度不等于AC段的平均速度,D错误.
答案:D
练1 解析:根据坐标分析可知轨迹为曲线,A项错误;位移为从(1,1)点到(3,3)点的有向线段,总位移为22 m,B项正确;机器人会两次通过同一点,C项错误;整个过程中平均速度v=xt=2222 m/s=1 m/s,D项错误.
答案:B
练2 解析:由v=△x△t可得该人在第2 s内的平均速度为2 m/s,B项正确;前4 s内的平均速度为v=1+2+3+44 m/s=2.5 m/s,C项正确;因该人的运动不是匀变速直线运动,故无法确定其瞬时速度大小,A、D项均错误.
答案:BC
例3 解析:点火后即将升空的火箭,火箭还没运动,但由于合外力不为零,加速度不为零,选项A错误;轿车紧急刹车,速度变化很快,根据加速度的定义式a=△v△t可知,加速度很大,选项B正确;高速行驶的磁悬浮列车,速度很大,但速度变化较小,加速度很小,选项C错误;100米比赛中,甲比乙跑得快,说明甲的速度大于乙的速度,选项D错误.
答案:B
例4 解析:方法一:取初速度的方向为正方向,即取着网前的速度方向为正方向,则v1=8 m/s,v2=-10 m/s,则a=v2-v1△t=-10-81.0 m/s2=-18 m/s2,负号说明加速度的方向与正方向相反,即向上,选项D正确.
方法二:取末速度的方向为正方向,即着网后的速度方向为正方向,则v1=-8 m/s,v2=10 m/s,则a=v2-v1△t=10+81.0 m/s2=18 m/s2,说明加速度的方向与正方向相同,选项D正确.
答案:D
例5 解析:速度变化量的方向与加速度方向一致,加速度方向与初速度方向相同时汽车做加速运动,加速度方向与初速度方向相反时汽车做减速运动.选项A中汽车做加速运动,选项B、C中分别是a的方向、Δv的方向作错了,选项D中图示能正确表示汽车做减速运动.故本题应选D.
答案:D
练3 解析:物体B的加速度大于物体A的加速度,可知物体B的速度变化比较快,故A错误,B正确.由于物体A、B的加速度方向与速度方向的关系未知,则无法判断物体A、B的速度是增加还是减小,故C、D错误.
答案:B
练4 解析:取初速度方向为正方向,则v0=5 m/s.若2 s后的速度方向沿斜面向上,v=3 m/s,则a=△v△t=v-v0△t=3-52 m/s2=-1 m/s2,即加速度大小为1 m/s2,方向沿斜面向下;若2 s后的速度方向沿斜面向下,v=-3 m/s,则a=△v△t=v-v0△t=-3-52 m/s2=-4 m/s2,即加速度大小为4 m/s2,方向沿斜面向下.故选项A、D错误,B、C正确.
答案:BC
思维拓展
典例1
解析:(1)v1=dΔt1=5×10-2m5×10-2s=1.0 m/s
v2=dΔt2=5×10-2m5×10-2s=2.5 m/s
(2)滑块宽度越小,挡光时间越短,平均速度越接近瞬时速度,误差越小.
答案:(1)1.0 2.5 (2)见解析
典例2 解析:(1)vB=AC2T=3.62+4.382×0.1×10-2 m/s=0.40 m/s
vF=EG2T=6.80+7.602×0.1×10-2 m/s=0.72 m/s
(2)计算时使用的频率偏大,时间间隔偏小,则测量的速度值偏大.
答案:(1)0.40 0.72 (2)偏大
典例3 解析:超声波信号从发出到被反射回来的时间间隔Δt=2.0 s,在1.0 s内,超声波前进距离为:x1=v声·12Δt=340×1 m=340 m;故汽车速度为:v=380-3401m/s=40 m/s;当测速仪接收到被反射回来的超声波信号时,汽车前进了:Δx=40×2 m=80 m,故C项正确.
答案:C
练1 解析:由题表知,四次实验的速度大小接近,挡光片的速度v=xt,计算可知Ⅳ的宽度最小,第四次实验测得的速度最接近小车车头到达光电门时的瞬时速度,D项正确.
答案:D
练2 解析:客车行驶示意图如图所示,设客车行驶速度为v1,声速为v2,客车第一次鸣笛时与悬崖距离为L,由题意有2L-v1×5 s=v2×5 s.
当客车第二次鸣笛时,客车距悬崖为L′,
则2L′-v1×3 s=v2×3 s.
又L′=L-v1×15 s,由以上各式,
解得v1=v214≈24.3 m/s=87.48 km/h<120 km/h.
故客车未超速.
答案:未超速
同课章节目录
