2020-2021学年 高一物理 牛顿第二定律的应用 强化学案Word版含答案
文档属性
| 名称 | 2020-2021学年 高一物理 牛顿第二定律的应用 强化学案Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-14 13:11:15 | ||
图片预览



文档简介
牛顿第二定律的应用
知识点一 牛顿第二定律的应用
1.动力学的两类基本问题
第一类:已知受力情况求物体的________.
第二类:已知运动情况求物体的________.
2.解决两类基本问题的方法
以________为“桥梁”,由运动学公式和________________列方程求解,具体逻辑关系如下
知识点二 超重与失重现象
1.视重
(1)当物体挂在弹簧测力计下或放在水平台秤上时,弹簧测力计或台秤的________称为视重.
(2)视重大小等于弹簧测力计所受物体的________或台秤所受物体的________.
2.超重
(1)定义:物体对支持物的压力(或对悬挂物的拉力)________物体所受重力的现象.
(2)产生条件:物体具有________的加速度.
3.失重
(1)定义:物体对支持物的压力(或对悬挂物的拉力)________物体所受重力的现象.
(2)产生条件:物体具有________的加速度.
4.完全失重
(1)定义:物体对支持物的压力(或对竖直悬挂物的拉力)________的现象称为完全失重现象.
(2)产生条件:物体的加速度a=____,方向竖直向下.
思考辨析
(1)相同质量的物体,加速度越大,所受合外力越大.( )
(2)物体加速度由运动状态决定,与所受力无关.( )
(3)物体加速度减小时,速度一定减小.( )
(4)质量不变的物体所受合外力发生变化,加速度也一定发生变化.( )
(5)人造地球卫星、宇宙飞船、航天飞机等航天器进入轨道后,其中的人和物将处于完全失重状态.
①完全失重时,人和物不再受重力作用.( )
②完全失重时,人和物处于平衡状态.( )
③航天飞机等航天器进入轨道后,具有指向地心的向心力加速度.( )
④物体处于超重或失重状态,由加速度的方向决定,与速度方向无关.( )
考点一 用牛顿第二定律求解瞬时加速度
师生共研
1.两种基本模型的特点
(1)轻绳不需要形变恢复时间,在瞬时问题中,其弹力可以突变,成为零或者别的值.
(2)轻弹簧(或者橡皮绳)需要较长的形变恢复时间,在瞬时问题中,当它两端始终有连接物时其弹力不能突变,大小和方向均不变.
2.求解瞬时加速度的一般思路
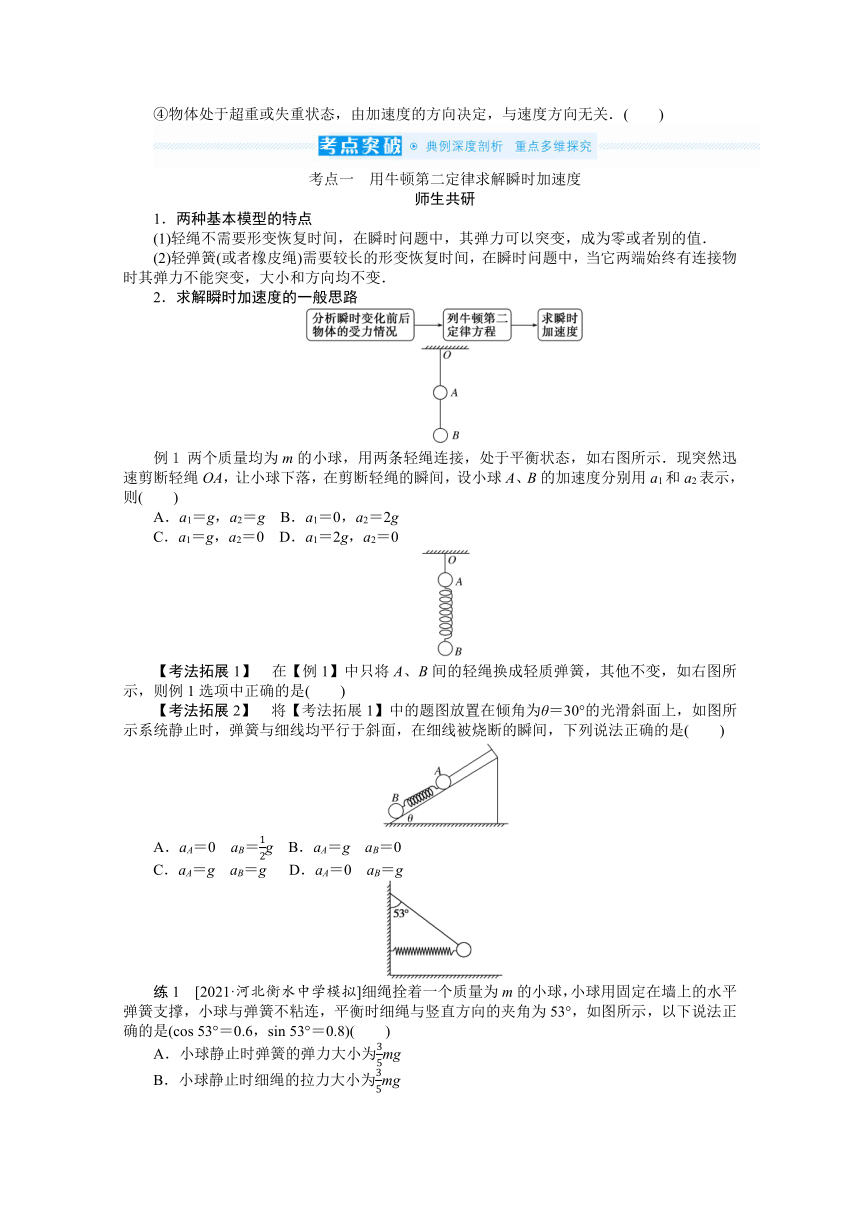
例1 两个质量均为m的小球,用两条轻绳连接,处于平衡状态,如右图所示.现突然迅速剪断轻绳OA,让小球下落,在剪断轻绳的瞬间,设小球A、B的加速度分别用a1和a2表示,则( )
A.a1=g,a2=g B.a1=0,a2=2g
C.a1=g,a2=0 D.a1=2g,a2=0
【考法拓展1】 在【例1】中只将A、B间的轻绳换成轻质弹簧,其他不变,如右图所示,则例1选项中正确的是( )
【考法拓展2】 将【考法拓展1】中的题图放置在倾角为θ=30°的光滑斜面上,如图所示系统静止时,弹簧与细线均平行于斜面,在细线被烧断的瞬间,下列说法正确的是( )
A.aA=0 aB=12g B.aA=g aB=0
C.aA=g aB=g D.aA=0 aB=g
练1 [2021·河北衡水中学模拟]细绳拴着一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为53°,如图所示,以下说法正确的是(cos 53°=0.6,sin 53°=0.8)( )
A.小球静止时弹簧的弹力大小为35mg
B.小球静止时细绳的拉力大小为35mg
C.细绳烧断瞬间小球的加速度立即变为g
D.细绳烧断瞬间小球的加速度立即变为53g
练2 [2021·陕西汉中月考]如图所示,质量均为m的木块A和B用一轻弹簧相连,竖直放在光滑的水平面上,木块A上放有质量为2m的木块C,三者均处于静止状态.现将木块C迅速移开,若重力加速度为g,则在木块C移开的瞬间( )
A.弹簧的形变量不改变
B.弹簧的弹力大小为mg
C.木块A的加速度大小为g
D.木块B对水平面的压力为3mg
考点二 动力学两类基本问题
多维探究
题型1|从受力确定运动情况
例2 滑冰车是儿童喜欢的冰上娱乐项目之一.如图所示为小明妈妈正与小明在冰上做游戏,小明与冰车的总质量是40 kg,冰车与冰面之间的动摩擦因数为0.05.在某次游戏中,假设小明妈妈对冰车施加了40 N的水平推力,使冰车从静止开始运动10 s后,停止施加力的作用,使冰车自由滑行.(假设运动过程中冰车始终沿直线运动,小明始终没有施加力的作用).求:
(1)冰车的最大速率.
(2)冰车在整个运动过程中滑行总位移的大小.
[教你解决问题]
【考法拓展1】 请根据【例2】中的情境,试求冰车一共滑行了多长时间?
【考法拓展2】 请根据【例2】中的情境,假设小明妈妈对冰车施加了40 N的水平推力,使冰车从静止开始运动5 s后,停止施加力的作用,则冰车之后自由滑行的时间是多少?
题型2|从运动情况确定受力情况
例3 如图所示,在地面上固定的两根竖直杆a、b之间搭建两个斜面1、2,已知斜面1与a杆的夹角为60°,斜面2与a杆的夹角为30°.现将一小物块(可视为质点)先后从斜面1、2的顶端(a杆处)由静止释放,两次到达斜面底端(b杆处)所用时间相等,若小物块与斜面1、2之间的动摩擦因数分别为μ1和μ2,重力加速度g取10 m/s2,则μ1:μ2等于( )
A.32 B. 33 C. 12 D. 13
练3 [2020·浙江模拟]绰号“威龙”的第五代制空战机歼—20具备高隐身性、高机动性能力,为防止极速提速过程中飞行员因缺氧晕厥,歼—20新型的抗荷服能帮助飞行员承受的最大加速度为重力加速度的9倍.假设某次垂直飞行测试实验中,歼—20加速达到50 m/s后离地,而后开始竖直向上做飞行试验.该飞机在10 s内匀加速到3 060 km/h,匀速飞行一段时间后到达最大飞行高度18.5 km.假设加速阶段所受阻力恒定,约为重力的15.已有该歼—20质量为20吨,g取10 m/s2,忽略战机因油耗等导致的质量变化.则下列说法正确的是( )
A.本次飞行测试的匀速阶段飞行时间为26.5 s
B.加速阶段系统的推力为1.84×106 N
C.加速阶段时飞行员有晕厥可能
D.飞机在匀速阶段时爬升高度为14.25 km
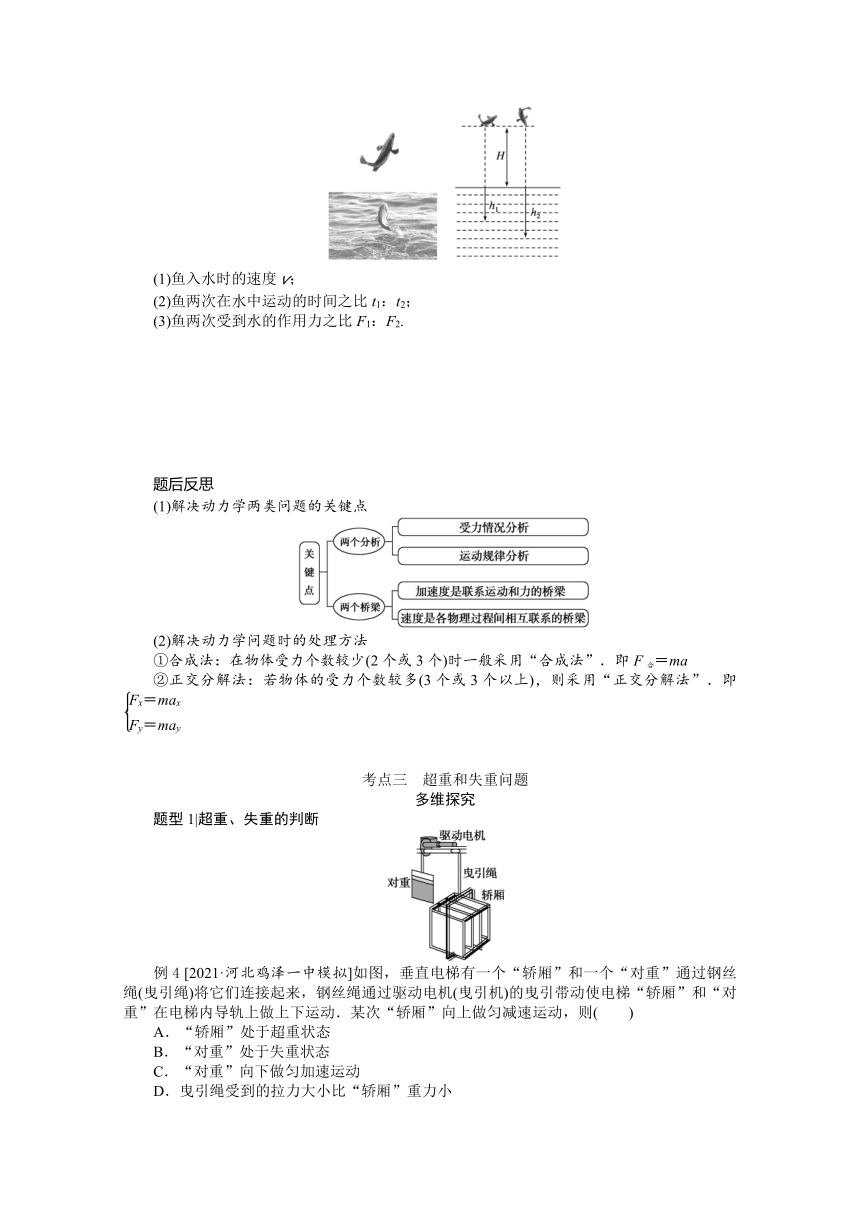
练4 如图所示,一条小鱼在水面处来了个“鲤鱼打挺”,弹起的高度为H=2h,以不同的姿态落入水中其入水深度不同.若鱼身水平,落入水中的深度为h1=h;若鱼身竖直,落入水中的深度为h2=1.5h.假定鱼的运动始终在竖直方向上,在水中保持姿态不变,受到水的作用力也不变,空气中的阻力不计,鱼身的尺寸远小于鱼入水深度.重力加速度为g,求:
(1)鱼入水时的速度v;
(2)鱼两次在水中运动的时间之比t1:t2;
(3)鱼两次受到水的作用力之比F1:F2.
题后反思
(1)解决动力学两类问题的关键点
(2)解决动力学问题时的处理方法
①合成法:在物体受力个数较少(2个或3个)时一般采用“合成法”.即F合=ma
②正交分解法:若物体的受力个数较多(3个或3个以上),则采用“正交分解法”.即
考点三 超重和失重问题
多维探究
题型1|超重、失重的判断
例4 [2021·河北鸡泽一中模拟]如图,垂直电梯有一个“轿厢”和一个“对重”通过钢丝绳(曳引绳)将它们连接起来,钢丝绳通过驱动电机(曳引机)的曳引带动使电梯“轿厢”和“对重”在电梯内导轨上做上下运动.某次“轿厢”向上做匀减速运动,则( )
A.“轿厢”处于超重状态
B.“对重”处于失重状态
C.“对重”向下做匀加速运动
D.曳引绳受到的拉力大小比“轿厢”重力小
题型2|利用牛顿第二定律解决超重、失重问题
例5 (多选)如图所示,电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为10 N,在某时刻电梯中的人观察到弹簧秤的示数变为6 N,关于电梯的运动,以下说法正确的是(g取10 m/s2)( )
A.电梯可能向上加速运动,加速度大小为4 m/s2
B.电梯可能向下加速运动,加速度大小为4 m/s2
C.电梯可能向上减速运动,加速度大小为4 m/s2
D.电梯可能向下减速运动,加速度大小为4 m/s2
题型3|超重、失重问题与图象的综合
例6 [2020·新高考Ⅰ卷,1]一质量为m的乘客乘坐竖直电梯下楼,其位移s与时间t的关系图象如图所示.乘客所受支持力的大小用FN表示,速度大小用v表示.重力加速度大小为g.以下判断正确的是( )
A.0~t1时间内,v增大,FN>mg
B.t1~t2时间内,v减小,FNC.t2~t3时间内,v增大,FND.t2~t3时间内,v减小,FN>mg
练5 质量为45 kg的小明同学站在升降机中的一“体重计”上,当升降机竖直向下运动经过5楼时,“体重计”示数为50 kg,如图所示,重力加速度取10 m/s2.此时小明处于( )
A.超重状态,对“体重计”压力为450 N
B.超重状态,对“体重计”压力为500 N
C.失重状态,对“体重计”压力为450 N
D.失重状态,对“体重计”压力为500 N
练6 图甲是某人站在接有传感器的力板上做下蹲、起跳和回落动作的示意图,图中的小黑点表示人的重心.图乙是力板所受压力随时间变化的图象,取重力加速度g=10 m/s2.根据图象分析可知( )
A.人的重力可由b点读出,约为300 N
B.b到c的过程中,人先处于超重状态再处于失重状态
C.人在双脚离开力板的过程中,处于完全失重状态
D.人在b点对应时刻的加速度大于在c点对应时刻的加速度
思维拓展
利用牛顿第二定律解决生活中的实际问题(STSE问题)
例1 [房顶的建筑]为了使雨滴能尽快地淌离房顶,要设计好房顶的高度,设雨滴沿房顶下淌时做无初速度无摩擦的运动,那么如图所示的四种情况中符合要求的是( )
例2 [逃生滑道]国产大飞机C919逃生系统打开后是一条倾斜的滑道,为了保证乘客的安全,乘客滑到地面的最大速度不能超过5 m/s.假设逃生口距地面的高度为4 m,人与滑道之间的动摩擦因数μ=0.5,重力加速度g取10 m/s2.求滑道打开后滑道的最小长度.
例3 [紧急避险车道]汽车连续下陡坡时,长时间的刹车会导致制动力下降,为保障安全,通常会在路旁设置向上的紧急避险车道,一种紧急避险车道由引道和制动床等组成,尽头是防撞设施,如图甲所示.质量为20 t的货车,以18 m/s的初速度冲向倾角θ=11.5°(sin 11.5°=0.2)的紧急避险车道,汽车在引道和制动床上的摩擦阻力分别是车重的0.30、0.80.引道长L1=30 m,制动床长L2=50 m,如图乙所示,取g=10 m/s2.
(1)求货车刚上引道时的加速度大小;
(2)货车将停在何处?是否会自行滑下?
(3)考虑到货车进入紧急避险车道速度最大可达到30 m/s,计算分析避险车道制动床长度的数据是否合理.
第2讲 牛顿第二定律的应用
基础落实
知识点一
1.运动情况 受力情况
2.加速度 牛顿第二定律
知识点二
1.(1)示数 (2)拉力 压力
2.(1)大于 (2)向上
3.(1)小于 (2)向下
4.(1)等于0 (2)g
思考辨析
(1)√ (2)× (3)× (4)√ (5)①× ②× ③√ ④√
考点突破
例1 解析:由于绳子张力可以突变,故剪断OA后小球A、B只受重力,其加速度a1=a2=g.故选项A正确.
答案:A
考法拓展1 解析:剪断轻绳OA的瞬间,由于弹簧弹力不能突变,故小球A所受合力为2mg,小球B所受合力为零,所以小球A、B的加速度分别为a1=2g,a2=0.故选项D正确.
答案:D
考法拓展2 解析:细线被烧断的瞬间,小球B的受力情况不变,加速度为零.烧断前,分析整体受力可知线的拉力为FT=2mgsin θ,烧断瞬间,A受的合力沿斜面向下,大小为2mgsin θ,所以A球的瞬时加速度为aA=2gsin 30°=g,故选项B正确.
答案:B
练1
解析:本题考查瞬时性问题.小球静止时,分析受力情况,如图所示,由平衡条件得弹簧的弹力F=mgtan 53°=43mg,细绳的拉力T=mgcos 53°=53mg,故A、B均错误;细绳烧断瞬间弹簧的弹力不变,则小球所受的合力与烧断前细绳拉力的大小相等、方向相反,则此瞬间小球的加速度大小为53g,故C错误,D正确.
答案:D
练2 解析:本题考查瞬时性问题.撤去C的瞬间,木块A还没有动,即木块A的位移为零,则弹簧的形变量不变,故A正确;开始时整体处于平衡状态,弹簧的弹力等于A和C的重力,即F=3mg,撤去C的瞬间,弹簧的形变量不变,弹簧的弹力不变,仍为3mg,故B错误;撤去C瞬间,弹力不变,A所受合力等于C的重力大小,对木块A,由牛顿第二定律得2mg=ma,解得a=2g,方向竖直向上,故C错误;撤去C的瞬间,弹簧的弹力不变,仍为3mg,对B,由平衡条件得F+mg=N,解得N=4mg,木块B对水平面的压力为4mg,故D错误.
答案:A
例2 解析:(1)以冰车及小明为研究对象,由牛顿第二定律得F-μmg=ma1①
vm=a1t②
由①②得vm=5 m/s.
(2)冰车匀加速运动过程中有
x1=12a1t2③
冰车自由滑行时有μmg=ma2④
vm2=2a2x2⑤
又x=x1+x2⑥
由③④⑤⑥得x=50 m
答案:(1)5 m/s (2)50 m
考法拓展1 解析:撤去推力后,冰车在摩擦力作用下做匀减速直线运动,最终速度为0
由运动学公式:0=vm-a2t′
解得t′=10 s
所以t总=t+t′=20 s
答案:20 s
考法拓展2 解析:由运动学公式得v′m=a1t1
解得v′m=2.5 m/s
停止施加力,冰车做匀减速直线运动由牛顿第二定律得μmg=ma2.
自由滑行时间t=vm'a2
代入数据解得t=5 s.
答案:5 s
例3 解析:设a、b之间的水平距离为L,到达斜面底端所用的时间为t,当物块在斜面1上运动时,有x=12at2得: Lsin 60°=12a1t2①
物块在斜面2上运动时,有x=12at2得:
Lsin 30°=12a2t2②
由牛顿第二定律得:
mgsin 30°-μ1mgcos 30°=ma1③
mgsin 60°-μ2mgcos 60°=ma2④
联立①②③④得μ1μ2=13,
故选项D正确.
答案:D
练3 解析:战机竖直向上加速阶段初速度v0=50 m/s,末速度v=3 060 km/h=850 m/s,根据v=v0+at得,加速度a=80 m/s2=8g,飞行员不会昏厥;根据牛顿第二定律,F-mg-f=ma,推力F=mg+f+ma=1.84×106 N,战机加速阶段上升的高度x=v0t+12at2=4 500 m,即匀速上升距离为14 km,匀速飞行时间t=sv=14000850 s≈16.5 s,故B正确.
答案:B
练4 解析:(1)由v2=2gH,得v=2gh
(2)因h1=v2t1,h2=v2t2,得t1t2=23
(3)v2=2a1h1,F1-mg=ma1
得F1=3mg,同理得F2=73mg,
所以F1F2=97
答案:(1)2gh (2)2?3 (3)9?7
例4 解析:本题考查超、失重的判断和理解.当“轿厢”向上做匀减速运动时,加速度向下,处于失重状态,选项A错误;“轿厢”失重,所以曳引绳的拉力小于其重力,选项D正确;同时,“对重”向下做匀减速运动,加速度向上,处于超重状态,选项B、C错误.
答案:D
例5 解析:电梯做匀速直线运动时,弹簧秤的示数为10 N,可知重物的重力等于10 N,在某时刻电梯中的人观察到弹簧秤的示数变为6 N,对重物,根据牛顿第二定律有mg-F=ma,解得a=4 m/s2,方向竖直向下,则电梯的加速度大小为4 m/s2,方向竖直向下,因此电梯可能向下做加速运动,也可能向上做减速运动,选项B、C正确.
答案:BC
例6 解析:根据位移-时间图象的斜率表示速度可知,0~t1时间内,图象斜率增大,速度v增大,加速度方向向下,由牛顿运动定律可知乘客处于失重状态,所受的支持力FNmg,选项C错误,D正确.
答案:D
练5 解析:小明的重力G=mg=45×10 N=450 N;由图可知,此时体重计示数为50 kg,故说明对体重计的压力为500 N,此时压力大于本身的重力,人处于超重状态,故B正确.A、C、D错误.
答案:B
练6 解析:本题考查根据起跳过程力的变化判断超失重状态.开始时人处于平衡状态,人对传感器的压力约为900 N,人的重力也约为900 N,故A错误;b到c的过程中,人先处于失重状态再处于超重状态,故B错误;双脚离开力板的过程中只受重力的作用,处于完全失重状态,故C正确;b点弹力与重力的差值要小于c点弹力与重力的差值,则人在b点的加速度要小于在c点的加速度,故D错误.
答案:C
思维拓展
典例1 解析:设屋檐的底角为θ,底边长为2L(不变).雨滴做初速度为零的匀加速直线运动,根据牛顿第二定律得加速度a=mgsin θm=gsin θ,位移大小x=12at2,而x=Lcos θ,2sin θcos θ=sin 2θ,联立以上各式得t=4Lgsin 2θ.当θ=45°时,sin 2θ=1为最大值,时间t最短,故选项C正确.
答案:C
典例2 解析:本题可以看成斜面模型,如图:
设滑道最短长度为x,此时滑道倾角为θ,乘客滑到地面时的速度v=52 m/s,
则有:sin θ=hx
cos θ=x2-h2x
设乘客质量为m,对沿滑道下滑的乘客受力分析可得:
mgsin θ-μmgcos θ=ma
对乘客的运动过程进行分析可得:v2=2ax
联立以上各式并代入数据可得x=5 m
素养考查:将逃生滑道建构成“斜面模型”,通过受力分析、运动分析列动力学方程,然后联立方程进行数学运算,渗透了“科学思维”素养中的“模型建构”及“科学推理”要素.“大飞机”项目是“大国重器”,是科技前沿和社会热点问题,学生通过做题,有一种“参与”设计的感受,渗透了“科学态度”与“社会责任”的素养要素.
典例3 解析:本题以紧急避险为背景考查牛顿运动定律问题.
(1)货车刚上引道时,对汽车受力分析,根据牛顿第二定律,有mgsin θ+k1mg=ma1,代入数据,得a1=5.0 m/s2.
(2)货车向上经过制动床时,有mgsin θ+k2mg=ma2,设货车在引道末端的速度为v1,根据运动学公式,有v12-v02=-2a1L1,设货车在进入制动床后,滑行x减速到零,有0-v12=-2a2x,联立解得x=1.2 m,即货车停在距离制动床底部1.2 m处;在引道上,有mgsin θ(3)设货车进入制动床xmax后车能停下来,根据动能定理,有-mg(L1+xmax)sin θ-k1mgL1-k2mgxmax=0-12mvmax2,代入数据,得xmax=30 m答案:(1)5.0 m/s2 (2)货车将停在距离制动床底部1.2 m处 不会自行滑下 (3)见解析
知识点一 牛顿第二定律的应用
1.动力学的两类基本问题
第一类:已知受力情况求物体的________.
第二类:已知运动情况求物体的________.
2.解决两类基本问题的方法
以________为“桥梁”,由运动学公式和________________列方程求解,具体逻辑关系如下
知识点二 超重与失重现象
1.视重
(1)当物体挂在弹簧测力计下或放在水平台秤上时,弹簧测力计或台秤的________称为视重.
(2)视重大小等于弹簧测力计所受物体的________或台秤所受物体的________.
2.超重
(1)定义:物体对支持物的压力(或对悬挂物的拉力)________物体所受重力的现象.
(2)产生条件:物体具有________的加速度.
3.失重
(1)定义:物体对支持物的压力(或对悬挂物的拉力)________物体所受重力的现象.
(2)产生条件:物体具有________的加速度.
4.完全失重
(1)定义:物体对支持物的压力(或对竖直悬挂物的拉力)________的现象称为完全失重现象.
(2)产生条件:物体的加速度a=____,方向竖直向下.
思考辨析
(1)相同质量的物体,加速度越大,所受合外力越大.( )
(2)物体加速度由运动状态决定,与所受力无关.( )
(3)物体加速度减小时,速度一定减小.( )
(4)质量不变的物体所受合外力发生变化,加速度也一定发生变化.( )
(5)人造地球卫星、宇宙飞船、航天飞机等航天器进入轨道后,其中的人和物将处于完全失重状态.
①完全失重时,人和物不再受重力作用.( )
②完全失重时,人和物处于平衡状态.( )
③航天飞机等航天器进入轨道后,具有指向地心的向心力加速度.( )
④物体处于超重或失重状态,由加速度的方向决定,与速度方向无关.( )
考点一 用牛顿第二定律求解瞬时加速度
师生共研
1.两种基本模型的特点
(1)轻绳不需要形变恢复时间,在瞬时问题中,其弹力可以突变,成为零或者别的值.
(2)轻弹簧(或者橡皮绳)需要较长的形变恢复时间,在瞬时问题中,当它两端始终有连接物时其弹力不能突变,大小和方向均不变.
2.求解瞬时加速度的一般思路
例1 两个质量均为m的小球,用两条轻绳连接,处于平衡状态,如右图所示.现突然迅速剪断轻绳OA,让小球下落,在剪断轻绳的瞬间,设小球A、B的加速度分别用a1和a2表示,则( )
A.a1=g,a2=g B.a1=0,a2=2g
C.a1=g,a2=0 D.a1=2g,a2=0
【考法拓展1】 在【例1】中只将A、B间的轻绳换成轻质弹簧,其他不变,如右图所示,则例1选项中正确的是( )
【考法拓展2】 将【考法拓展1】中的题图放置在倾角为θ=30°的光滑斜面上,如图所示系统静止时,弹簧与细线均平行于斜面,在细线被烧断的瞬间,下列说法正确的是( )
A.aA=0 aB=12g B.aA=g aB=0
C.aA=g aB=g D.aA=0 aB=g
练1 [2021·河北衡水中学模拟]细绳拴着一个质量为m的小球,小球用固定在墙上的水平弹簧支撑,小球与弹簧不粘连,平衡时细绳与竖直方向的夹角为53°,如图所示,以下说法正确的是(cos 53°=0.6,sin 53°=0.8)( )
A.小球静止时弹簧的弹力大小为35mg
B.小球静止时细绳的拉力大小为35mg
C.细绳烧断瞬间小球的加速度立即变为g
D.细绳烧断瞬间小球的加速度立即变为53g
练2 [2021·陕西汉中月考]如图所示,质量均为m的木块A和B用一轻弹簧相连,竖直放在光滑的水平面上,木块A上放有质量为2m的木块C,三者均处于静止状态.现将木块C迅速移开,若重力加速度为g,则在木块C移开的瞬间( )
A.弹簧的形变量不改变
B.弹簧的弹力大小为mg
C.木块A的加速度大小为g
D.木块B对水平面的压力为3mg
考点二 动力学两类基本问题
多维探究
题型1|从受力确定运动情况
例2 滑冰车是儿童喜欢的冰上娱乐项目之一.如图所示为小明妈妈正与小明在冰上做游戏,小明与冰车的总质量是40 kg,冰车与冰面之间的动摩擦因数为0.05.在某次游戏中,假设小明妈妈对冰车施加了40 N的水平推力,使冰车从静止开始运动10 s后,停止施加力的作用,使冰车自由滑行.(假设运动过程中冰车始终沿直线运动,小明始终没有施加力的作用).求:
(1)冰车的最大速率.
(2)冰车在整个运动过程中滑行总位移的大小.
[教你解决问题]
【考法拓展1】 请根据【例2】中的情境,试求冰车一共滑行了多长时间?
【考法拓展2】 请根据【例2】中的情境,假设小明妈妈对冰车施加了40 N的水平推力,使冰车从静止开始运动5 s后,停止施加力的作用,则冰车之后自由滑行的时间是多少?
题型2|从运动情况确定受力情况
例3 如图所示,在地面上固定的两根竖直杆a、b之间搭建两个斜面1、2,已知斜面1与a杆的夹角为60°,斜面2与a杆的夹角为30°.现将一小物块(可视为质点)先后从斜面1、2的顶端(a杆处)由静止释放,两次到达斜面底端(b杆处)所用时间相等,若小物块与斜面1、2之间的动摩擦因数分别为μ1和μ2,重力加速度g取10 m/s2,则μ1:μ2等于( )
A.32 B. 33 C. 12 D. 13
练3 [2020·浙江模拟]绰号“威龙”的第五代制空战机歼—20具备高隐身性、高机动性能力,为防止极速提速过程中飞行员因缺氧晕厥,歼—20新型的抗荷服能帮助飞行员承受的最大加速度为重力加速度的9倍.假设某次垂直飞行测试实验中,歼—20加速达到50 m/s后离地,而后开始竖直向上做飞行试验.该飞机在10 s内匀加速到3 060 km/h,匀速飞行一段时间后到达最大飞行高度18.5 km.假设加速阶段所受阻力恒定,约为重力的15.已有该歼—20质量为20吨,g取10 m/s2,忽略战机因油耗等导致的质量变化.则下列说法正确的是( )
A.本次飞行测试的匀速阶段飞行时间为26.5 s
B.加速阶段系统的推力为1.84×106 N
C.加速阶段时飞行员有晕厥可能
D.飞机在匀速阶段时爬升高度为14.25 km
练4 如图所示,一条小鱼在水面处来了个“鲤鱼打挺”,弹起的高度为H=2h,以不同的姿态落入水中其入水深度不同.若鱼身水平,落入水中的深度为h1=h;若鱼身竖直,落入水中的深度为h2=1.5h.假定鱼的运动始终在竖直方向上,在水中保持姿态不变,受到水的作用力也不变,空气中的阻力不计,鱼身的尺寸远小于鱼入水深度.重力加速度为g,求:
(1)鱼入水时的速度v;
(2)鱼两次在水中运动的时间之比t1:t2;
(3)鱼两次受到水的作用力之比F1:F2.
题后反思
(1)解决动力学两类问题的关键点
(2)解决动力学问题时的处理方法
①合成法:在物体受力个数较少(2个或3个)时一般采用“合成法”.即F合=ma
②正交分解法:若物体的受力个数较多(3个或3个以上),则采用“正交分解法”.即
考点三 超重和失重问题
多维探究
题型1|超重、失重的判断
例4 [2021·河北鸡泽一中模拟]如图,垂直电梯有一个“轿厢”和一个“对重”通过钢丝绳(曳引绳)将它们连接起来,钢丝绳通过驱动电机(曳引机)的曳引带动使电梯“轿厢”和“对重”在电梯内导轨上做上下运动.某次“轿厢”向上做匀减速运动,则( )
A.“轿厢”处于超重状态
B.“对重”处于失重状态
C.“对重”向下做匀加速运动
D.曳引绳受到的拉力大小比“轿厢”重力小
题型2|利用牛顿第二定律解决超重、失重问题
例5 (多选)如图所示,电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯匀速直线运动时,弹簧秤的示数为10 N,在某时刻电梯中的人观察到弹簧秤的示数变为6 N,关于电梯的运动,以下说法正确的是(g取10 m/s2)( )
A.电梯可能向上加速运动,加速度大小为4 m/s2
B.电梯可能向下加速运动,加速度大小为4 m/s2
C.电梯可能向上减速运动,加速度大小为4 m/s2
D.电梯可能向下减速运动,加速度大小为4 m/s2
题型3|超重、失重问题与图象的综合
例6 [2020·新高考Ⅰ卷,1]一质量为m的乘客乘坐竖直电梯下楼,其位移s与时间t的关系图象如图所示.乘客所受支持力的大小用FN表示,速度大小用v表示.重力加速度大小为g.以下判断正确的是( )
A.0~t1时间内,v增大,FN>mg
B.t1~t2时间内,v减小,FN
练5 质量为45 kg的小明同学站在升降机中的一“体重计”上,当升降机竖直向下运动经过5楼时,“体重计”示数为50 kg,如图所示,重力加速度取10 m/s2.此时小明处于( )
A.超重状态,对“体重计”压力为450 N
B.超重状态,对“体重计”压力为500 N
C.失重状态,对“体重计”压力为450 N
D.失重状态,对“体重计”压力为500 N
练6 图甲是某人站在接有传感器的力板上做下蹲、起跳和回落动作的示意图,图中的小黑点表示人的重心.图乙是力板所受压力随时间变化的图象,取重力加速度g=10 m/s2.根据图象分析可知( )
A.人的重力可由b点读出,约为300 N
B.b到c的过程中,人先处于超重状态再处于失重状态
C.人在双脚离开力板的过程中,处于完全失重状态
D.人在b点对应时刻的加速度大于在c点对应时刻的加速度
思维拓展
利用牛顿第二定律解决生活中的实际问题(STSE问题)
例1 [房顶的建筑]为了使雨滴能尽快地淌离房顶,要设计好房顶的高度,设雨滴沿房顶下淌时做无初速度无摩擦的运动,那么如图所示的四种情况中符合要求的是( )
例2 [逃生滑道]国产大飞机C919逃生系统打开后是一条倾斜的滑道,为了保证乘客的安全,乘客滑到地面的最大速度不能超过5 m/s.假设逃生口距地面的高度为4 m,人与滑道之间的动摩擦因数μ=0.5,重力加速度g取10 m/s2.求滑道打开后滑道的最小长度.
例3 [紧急避险车道]汽车连续下陡坡时,长时间的刹车会导致制动力下降,为保障安全,通常会在路旁设置向上的紧急避险车道,一种紧急避险车道由引道和制动床等组成,尽头是防撞设施,如图甲所示.质量为20 t的货车,以18 m/s的初速度冲向倾角θ=11.5°(sin 11.5°=0.2)的紧急避险车道,汽车在引道和制动床上的摩擦阻力分别是车重的0.30、0.80.引道长L1=30 m,制动床长L2=50 m,如图乙所示,取g=10 m/s2.
(1)求货车刚上引道时的加速度大小;
(2)货车将停在何处?是否会自行滑下?
(3)考虑到货车进入紧急避险车道速度最大可达到30 m/s,计算分析避险车道制动床长度的数据是否合理.
第2讲 牛顿第二定律的应用
基础落实
知识点一
1.运动情况 受力情况
2.加速度 牛顿第二定律
知识点二
1.(1)示数 (2)拉力 压力
2.(1)大于 (2)向上
3.(1)小于 (2)向下
4.(1)等于0 (2)g
思考辨析
(1)√ (2)× (3)× (4)√ (5)①× ②× ③√ ④√
考点突破
例1 解析:由于绳子张力可以突变,故剪断OA后小球A、B只受重力,其加速度a1=a2=g.故选项A正确.
答案:A
考法拓展1 解析:剪断轻绳OA的瞬间,由于弹簧弹力不能突变,故小球A所受合力为2mg,小球B所受合力为零,所以小球A、B的加速度分别为a1=2g,a2=0.故选项D正确.
答案:D
考法拓展2 解析:细线被烧断的瞬间,小球B的受力情况不变,加速度为零.烧断前,分析整体受力可知线的拉力为FT=2mgsin θ,烧断瞬间,A受的合力沿斜面向下,大小为2mgsin θ,所以A球的瞬时加速度为aA=2gsin 30°=g,故选项B正确.
答案:B
练1
解析:本题考查瞬时性问题.小球静止时,分析受力情况,如图所示,由平衡条件得弹簧的弹力F=mgtan 53°=43mg,细绳的拉力T=mgcos 53°=53mg,故A、B均错误;细绳烧断瞬间弹簧的弹力不变,则小球所受的合力与烧断前细绳拉力的大小相等、方向相反,则此瞬间小球的加速度大小为53g,故C错误,D正确.
答案:D
练2 解析:本题考查瞬时性问题.撤去C的瞬间,木块A还没有动,即木块A的位移为零,则弹簧的形变量不变,故A正确;开始时整体处于平衡状态,弹簧的弹力等于A和C的重力,即F=3mg,撤去C的瞬间,弹簧的形变量不变,弹簧的弹力不变,仍为3mg,故B错误;撤去C瞬间,弹力不变,A所受合力等于C的重力大小,对木块A,由牛顿第二定律得2mg=ma,解得a=2g,方向竖直向上,故C错误;撤去C的瞬间,弹簧的弹力不变,仍为3mg,对B,由平衡条件得F+mg=N,解得N=4mg,木块B对水平面的压力为4mg,故D错误.
答案:A
例2 解析:(1)以冰车及小明为研究对象,由牛顿第二定律得F-μmg=ma1①
vm=a1t②
由①②得vm=5 m/s.
(2)冰车匀加速运动过程中有
x1=12a1t2③
冰车自由滑行时有μmg=ma2④
vm2=2a2x2⑤
又x=x1+x2⑥
由③④⑤⑥得x=50 m
答案:(1)5 m/s (2)50 m
考法拓展1 解析:撤去推力后,冰车在摩擦力作用下做匀减速直线运动,最终速度为0
由运动学公式:0=vm-a2t′
解得t′=10 s
所以t总=t+t′=20 s
答案:20 s
考法拓展2 解析:由运动学公式得v′m=a1t1
解得v′m=2.5 m/s
停止施加力,冰车做匀减速直线运动由牛顿第二定律得μmg=ma2.
自由滑行时间t=vm'a2
代入数据解得t=5 s.
答案:5 s
例3 解析:设a、b之间的水平距离为L,到达斜面底端所用的时间为t,当物块在斜面1上运动时,有x=12at2得: Lsin 60°=12a1t2①
物块在斜面2上运动时,有x=12at2得:
Lsin 30°=12a2t2②
由牛顿第二定律得:
mgsin 30°-μ1mgcos 30°=ma1③
mgsin 60°-μ2mgcos 60°=ma2④
联立①②③④得μ1μ2=13,
故选项D正确.
答案:D
练3 解析:战机竖直向上加速阶段初速度v0=50 m/s,末速度v=3 060 km/h=850 m/s,根据v=v0+at得,加速度a=80 m/s2=8g,飞行员不会昏厥;根据牛顿第二定律,F-mg-f=ma,推力F=mg+f+ma=1.84×106 N,战机加速阶段上升的高度x=v0t+12at2=4 500 m,即匀速上升距离为14 km,匀速飞行时间t=sv=14000850 s≈16.5 s,故B正确.
答案:B
练4 解析:(1)由v2=2gH,得v=2gh
(2)因h1=v2t1,h2=v2t2,得t1t2=23
(3)v2=2a1h1,F1-mg=ma1
得F1=3mg,同理得F2=73mg,
所以F1F2=97
答案:(1)2gh (2)2?3 (3)9?7
例4 解析:本题考查超、失重的判断和理解.当“轿厢”向上做匀减速运动时,加速度向下,处于失重状态,选项A错误;“轿厢”失重,所以曳引绳的拉力小于其重力,选项D正确;同时,“对重”向下做匀减速运动,加速度向上,处于超重状态,选项B、C错误.
答案:D
例5 解析:电梯做匀速直线运动时,弹簧秤的示数为10 N,可知重物的重力等于10 N,在某时刻电梯中的人观察到弹簧秤的示数变为6 N,对重物,根据牛顿第二定律有mg-F=ma,解得a=4 m/s2,方向竖直向下,则电梯的加速度大小为4 m/s2,方向竖直向下,因此电梯可能向下做加速运动,也可能向上做减速运动,选项B、C正确.
答案:BC
例6 解析:根据位移-时间图象的斜率表示速度可知,0~t1时间内,图象斜率增大,速度v增大,加速度方向向下,由牛顿运动定律可知乘客处于失重状态,所受的支持力FN
答案:D
练5 解析:小明的重力G=mg=45×10 N=450 N;由图可知,此时体重计示数为50 kg,故说明对体重计的压力为500 N,此时压力大于本身的重力,人处于超重状态,故B正确.A、C、D错误.
答案:B
练6 解析:本题考查根据起跳过程力的变化判断超失重状态.开始时人处于平衡状态,人对传感器的压力约为900 N,人的重力也约为900 N,故A错误;b到c的过程中,人先处于失重状态再处于超重状态,故B错误;双脚离开力板的过程中只受重力的作用,处于完全失重状态,故C正确;b点弹力与重力的差值要小于c点弹力与重力的差值,则人在b点的加速度要小于在c点的加速度,故D错误.
答案:C
思维拓展
典例1 解析:设屋檐的底角为θ,底边长为2L(不变).雨滴做初速度为零的匀加速直线运动,根据牛顿第二定律得加速度a=mgsin θm=gsin θ,位移大小x=12at2,而x=Lcos θ,2sin θcos θ=sin 2θ,联立以上各式得t=4Lgsin 2θ.当θ=45°时,sin 2θ=1为最大值,时间t最短,故选项C正确.
答案:C
典例2 解析:本题可以看成斜面模型,如图:
设滑道最短长度为x,此时滑道倾角为θ,乘客滑到地面时的速度v=52 m/s,
则有:sin θ=hx
cos θ=x2-h2x
设乘客质量为m,对沿滑道下滑的乘客受力分析可得:
mgsin θ-μmgcos θ=ma
对乘客的运动过程进行分析可得:v2=2ax
联立以上各式并代入数据可得x=5 m
素养考查:将逃生滑道建构成“斜面模型”,通过受力分析、运动分析列动力学方程,然后联立方程进行数学运算,渗透了“科学思维”素养中的“模型建构”及“科学推理”要素.“大飞机”项目是“大国重器”,是科技前沿和社会热点问题,学生通过做题,有一种“参与”设计的感受,渗透了“科学态度”与“社会责任”的素养要素.
典例3 解析:本题以紧急避险为背景考查牛顿运动定律问题.
(1)货车刚上引道时,对汽车受力分析,根据牛顿第二定律,有mgsin θ+k1mg=ma1,代入数据,得a1=5.0 m/s2.
(2)货车向上经过制动床时,有mgsin θ+k2mg=ma2,设货车在引道末端的速度为v1,根据运动学公式,有v12-v02=-2a1L1,设货车在进入制动床后,滑行x减速到零,有0-v12=-2a2x,联立解得x=1.2 m,即货车停在距离制动床底部1.2 m处;在引道上,有mgsin θ
同课章节目录
