平面直角坐标系（1）课件

(共17张PPT)
什么是数轴？
规定了原点、正方向、单位长度的直线叫做数轴。
回顾 & 思考

数轴上的点A表示2.
D
B
A
C
口答
点B表示的数是 :
-1在数轴上的位置是 :
-3
D
0
1
2
3
4
-3
-2
-1
.
反过来，2在数轴上的位置就是点A。
数轴上的点与实数是一一对应的.
3
1
2
-2
-4
-1
-3
0
1
2
3
4
-4
-3
-2
-1
x
横轴
y
纵轴
·
A
在神舟六号着落时，地面搜救人员找到后如何迅速的报告精确的着落地点？
实际上这都有赖于
“卫星全球定位仪”
GPS，因为全球任
何一个地方都存在
唯一的经度和纬度。
我们可以利用GPS
测得神州六号飞船
的返回仓着落地的
经度和纬度 ．
内蒙古四王子旗
东经112.30,北纬42.50
哪一个水兵与众不同？你能说出具体的位置吗？
你能举出生活中用实数对确定位置的例子吗
说一说
6.1.1有序数对
乘
9排7号
7排9号
带眼镜的同学有占位了吗？
1、数对中的两个数是有顺序的
2、数对中的两个数所表示的含义是不同的
我们把这种有顺序的两个实数a与b组成的数对叫做有序实数对，记作(a,b)
有序实数对：
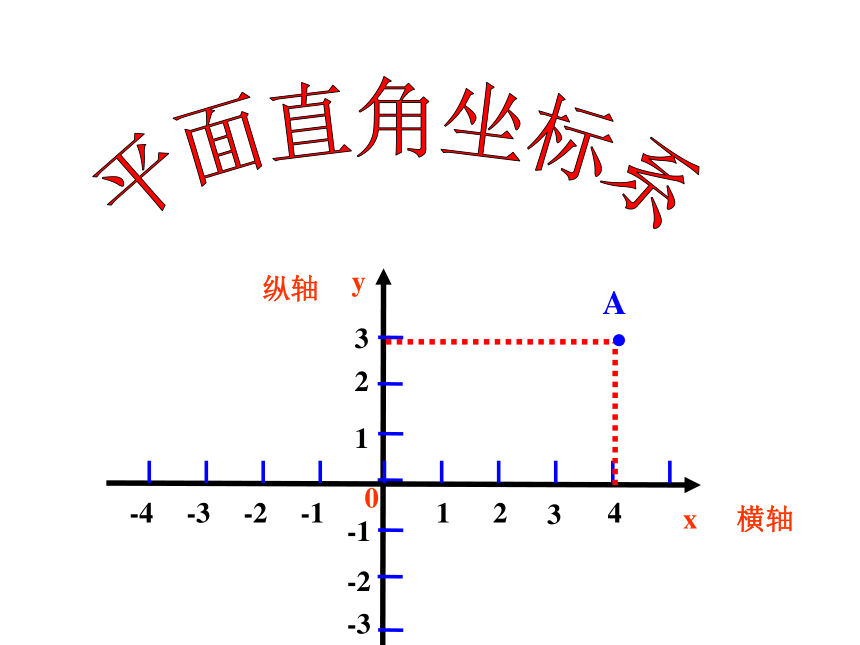
数轴上点的位置可以用一个数来表示,平面内的
点可以用有序实数对来表示，因此需用两条数轴　　　　　．
0
2
3
1
-1
-2
-3
3
1
2
-1
-3
-2
平面内两条原点重合、互相垂直的数轴,构成平面直角坐标系.
x轴(横轴)
y轴(纵轴)
原点
P
P点的横坐标是2
P点的纵坐标是3
有序实数对(2,3)就叫做P的坐标
记为P(2,3)
2
A
B
C
D
4
3
2
0
1
1
-1
5
-2
-3
-4
5
4
3
-4
-3
-2
-1
你能确定A、B、C、D四点的坐标吗
做一做
B(-3,-4)
C(0, 2)
D(-4,0)
x
y
A(3,4)
A
B
C
D
4
3
2
0
1
2
1
-1
5
-2
-3
-4
5
4
3
-4
-3
-2
-1
B(-3,-4)
C(0,2)
D(-4,0)
x
y
A(3,4)
建立了平面直角坐标系后,坐标平面就被坐标轴分成了Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
第一象限
第三象限
坐标轴上的点不属于任何象限
y轴上
x轴上
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B(-2,3)
·
A(4,3)
·
D(2,-2)
·
C(-4,-1)
E(0,-1)
F(5,0)
例.在直角坐标系中，描出下列各点:A(4,3), B(-2,3),
C(-4,-1)，D(2,-2)， E(0,-1) , F(5,0)
结论:平面直角坐标系中的点与有序实数对是一一对应的.
思考:(1)在四个象限内的点的坐标各有什么特征
(2)两条坐标轴上的点的坐标各有什么特征
3
1
4
2
5
-2
-4
-1
-3
1
2
3
4
5
-4
-3
-2
-1
y
第一象限
第二象限
第三象限
第四象限
结论
x轴上的点纵坐标为0
y轴上的点横坐标为0
(+, +)
(-, +)
(-, -)
(+, -)
x
2、已知点A(x-1,3+x)在第二象限内,则x的取值范围 。
3、点B(-3,-4)到x轴的距离是 ,到y轴的距离是 ,
到原点的距离是 .
-3x
y
0
-3
-4
B
4
3
5
1、点P(-2.5,-1.2)位于第 象限,
点Q（0.5，-0.8）是第 象限内的点。
三
四
已知A(1,4),B(-4,0),C(2,0).
则△ABC的面积是＿＿＿＿＿．
y
A
C
O
(1,4)
(-4,0)
(2,0)
B
12
若B、C的坐标不变, △ABC的
面积为6,点A的横坐标为-1,那么点A的坐标为 。
C
A
B
(-4,0)
(2,0)
y
O
A′
(-1,2)或(-1,-2)
作业
这节课你有哪些收获
想一想
用有序数对表示平面直角坐标系中任意一个点的位置
知道一个点能写出它的坐标
知道一个点的坐标,能描出这个点
各象限内的点的坐标的符号
平面直角坐标系
P31
练习1、2