华师大版八年级数学下册第17章 函数及其图象测试题 (word版含答案)
文档属性
| 名称 | 华师大版八年级数学下册第17章 函数及其图象测试题 (word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 00:00:00 | ||
图片预览


文档简介
第17章
函数及其图象测试题
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.
下列函数:①y=2x﹣1;②y=﹣;③y=;④y=x2.其中一次函数有( )
A.1个
B.2个
C.3个
D.4个
2.在平面直角坐标系中,若点A(-m,n)在第四象限,则点B(1-n,m)在( )
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
3.弹簧挂上物体后会伸长,测得一弹簧的长度y
(cm)与所挂物体的质量x(kg)之间有下面的关系:
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
下列说法不正确的是(
)
弹簧不挂重物时的长度为20
cm
x与y都是变量,
x是自变量,y是x的函数
物体质量每增加1
kg,弹簧的长度y增加0.5
cm
D.所挂物体质量为7
kg时,弹簧的长度为24
cm
4.要得到直线的图象,可以把直线(
)
A.向上平移4个单位长度
B.向下平移4个单位长度
C.向左平移4个单位长度
D.向右平移4个单位长度
5.已知直角坐标系中点P到y轴的距离为5,且点P到x轴的距离为3,则这样的点P的个数是(
)
A.1
B.2
C.3
D.4
6.
若一个正比例函数的图象经过不同象限的两点
A(m,-1)B(-5,n)则下列判断正确的是(
)
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0
7.
如图1,已知A为反比例函数y=(x<0)图象上一点,过点A作AB⊥y轴,垂足为B.若△OAB的面积为2,则k的值为( )
A.2
B.﹣2
C.4
D.﹣4
图1
图2
图3
图4
8.
如图2,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB长为半径画弧,交x轴正半轴于点C,则点C的坐标为( )
A.(,0)
B.(-2,0)
C.(2-,0)
D.(0,-2)
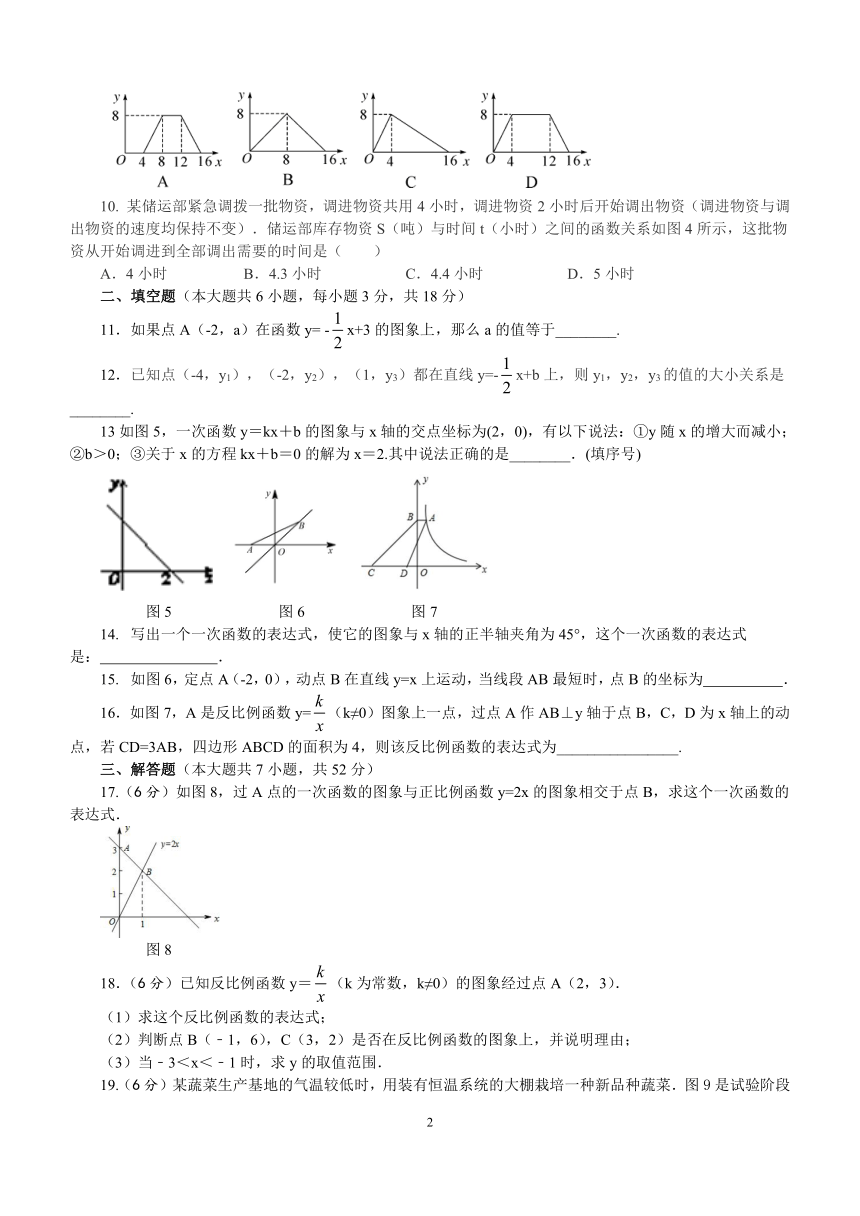
9.如图3,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A.设P点经过的路程为x,以点A,P,D为顶点的三角形的面积为y,则下列图象能大致反映y与x的函数关系的是( )
10.
某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图4所示,这批物资从开始调进到全部调出需要的时间是( )
A.4小时
B.4.3小时
C.4.4小时
D.5小时
二、填空题(本大题共6小题,每小题3分,共18分)
11.如果点A(-2,a)在函数y=
-x+3的图象上,那么a的值等于________.
12.已知点(-4,y1),(-2,y2),(1,y3)都在直线y=-x+b上,则y1,y2,y3的值的大小关系是________.
13如图5,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),有以下说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.其中说法正确的是________.(填序号)
图5
图6
图7
写出一个一次函数的表达式,使它的图象与x轴的正半轴夹角为45°,这个一次函数的表达式是:
?.
如图6,定点A(-2,0),动点B在直线y=x上运动,当线段AB最短时,点B的坐标为
?.
16.如图7,A是反比例函数y=(k≠0)图象上一点,过点A作AB⊥y轴于点B,C,D为x轴上的动点,若CD=3AB,四边形ABCD的面积为4,则该反比例函数的表达式为________________.
三、解答题(本大题共7小题,共52分)
17.(6分)如图8,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,求这个一次函数的表达式.
图8
18.(6分)已知反比例函数y=(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个反比例函数的表达式;
(2)判断点B(﹣1,6),C(3,2)是否在反比例函数的图象上,并说明理由;
(3)当﹣3<x<﹣1时,求y的取值范围.
19.(6分)某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.图9是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问:这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
图9
20.(8分)已知一次函数y=-2x-2.
(1)根据关系式在图10中画出函数的图象;
(2)求出图象与x轴,y轴的交点A,B的坐标;
(3)求A,B两点间的距离.
(4)y的值随x值的增大怎样变化?
图10
图11
21.(8分)甲、乙两车同时从A地出发驶向B地.甲车到达B地后立即返回,设甲车离A地的距离为y1(千米),乙车离A地的距离为y2(千米),行驶时间为x(小时),y1,y2与x的函数关系如图11所示.
(1)填空:A,B两地相距______千米,甲车从B地返回A地的行驶速度是______千米/时;
(2)当两车行驶7小时后在途中相遇,求点E的坐标;
(3)甲车从B地返回A地途中,与乙车相距100千米时,求甲车行驶的时间.
22.(8分)如图12,在平面直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,写出点C的坐标;
(3)点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
图12
图13
23.
(10分)如图13,已知直线AB分别交x轴和y轴与B、A两点,A(0,﹣3),B(2,0).
(1)求直线AB的表达式;
(2)将线段AB平移至DC的位置,其点D在x轴的负半轴上,点C在反比例函数y=的图象上,若S△BCD=18,求反比例函数的表达式;
(3)设BC交y轴于点P,求S△ABP.
附加题(20分,不计入总分)
24.【原题重现】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图14中的折线表示y与x之间的函数关系.
……
若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
【问题再研】
若设慢车行驶的时间为x(h),慢车与甲地的距离为s1(km),第一列快车与甲地的距离为s2(km),第二列快车与甲地的距离为s3(km),根据原题中所给信息解决下列问题:
(1)在同一直角坐标系中,分别画出s1,s2与x之间的函数图象;
(2)求s3与x之间的函数关系式;
(3)求原题的答案.
图14
第17章
函数及其图象测试题
一、1.
B
2.D
3.
D
4.
B
5.
D
6.
A
7.
D
8.
B
9.
A
10.
C
10.
C
提示:由图中可以看出,2小时调进物资3吨,调进物资共用4小时,即物资一共有6吨;2小时后,调进物资和调出物资同时进行,4小时时,物资调进完毕,仓库还剩1吨,说明调出的速度为(6-1)÷2=2.5(吨/时),调出所需时间为6÷2.5=2.4(小时),所以一共的时间是2+2.4=4.4(小时).
二、11.
4
12.
y1>y2>y3
13.
①②③
14.
答案不唯一,如y=-x+1
15.(-1,-1)
16.
三、17.
解:因为点B在正比例函数y=2x的图象上,横坐标为1,所以y=2×1=2.所以B(1,2).
设一次函数的表达式为y=kx+b.将A(0,3),B(1,2)代入,得b=3,k+b=2,解得k=-1.
所以这个一次函数的表达式为y=﹣x+3.
18.
(1)y=.
(2)B(﹣1,6)不在反比例函数的图象上,C(3,2)在反比例函数的图象上.理由略.
(3)﹣6<y<﹣2.
19.
解:(1)
(2)由(1)知恒温系统设定恒温为20°C.
(3)把y=10代入y=
中,解得x=20.20-10=10(小时).
答:恒温系统最多关闭10小时,蔬菜才能避免受到伤害
20.
解:(1)在y=-2x-2中,令y=0,可得x=-1;令x=0,可得y=-2.
所以图象是过(-1,0)和(0,-2)的一条直线,其图象如图1所示.
(2)由(1)可知A(-1,0),B(0,-2).
(3)因为A(-1,0),B(0,-2),所以OA=1,OB=2.所以AB==,即A,B两点间的距离为.
(4)因为在y=-2x-2中,k=-2<0,所以y随x的增大而减小.
21.
解:(1)800
100
(2)乙车行驶的时间为7小时,行驶的路程为800-100×(7-6)=700,所以E(7,700).
(3)设相遇前经过x小时甲、乙两车相距100千米.
则有100x+100+100(x-6)=800,解得x=6.5;
设相遇后经过x小时,甲、乙两车相距100千米.
则有100x+100(x-6)-100=800,解得x=7.5.
所以甲车行驶的时间是6.5小时或7.5小时时,两车相距100千米.
22.
解:(1)将点A(2,0)代入y=kx+3,得0=2k+3,解得k=
-.
所以y=
-x+3.
当x=0时,y=3.所以B(0,3),OB=3.
当y=0时,-x+3=0,解得x=2.
所以A(2,0),OA=2.
所以S△AOB=OA?OB=×2×3=3.
(2)如图2,①当AB=BC时,点C与点A(2,0)关于y轴对称,所以C(-2,0);
②当AB=AC时,由OA=2,OB=3,得AB==,由AB=AC′=AC″=,得C′(+2,0),C″(-2,0).
综上所述,符合条件的点C的坐标是(-2,0),(+2,0)或(-2,0).
图2
图3
图4
(3)因为M(0,3),所以OM=3.所以AM=3-2=1.由(1)知,S△AOB=3,所以S△PBM=S△AOB=3.
①如图3,当点P在x轴下方时,S△PBM=S△ABM+S△APM=+?AM?|yP|=+×1×|yP|=3.所以|yP|=3.
因为点P在x轴下方,所以yP=-3.将y=-3代入y=-x+3,得-3=-x+3,解得x=4.所以P(4,-3);
②如图3,当点P在x轴上方时,S△PBM=S△PAM-S△ABM=?AM?|yP|-=×1×|yP|-=3.所以|yP|=9.
因为点P在x轴上方,所以yP=9.将y=9代入y=-x+3,得9=
-x+3,解得x=-4.所以P(-4,9).
23.
解:(1)设直线AB的表达式为y=kx+b(k≠0).
将A(0,﹣3),B(2,0)代入,得解得
所以直线AB的表达式为y=x﹣3.
(2)由A(0,﹣3),B(2,0),将线段AB平移至DC的位置,得D(xD,0),C(xD+2,3).
又因为S△BCD=BD×3=18,所以|(xD﹣2)|×3=18.所以xD=﹣10.
所以D(﹣10,0),C(﹣8,3).
因为点C在反比例函数y=的图象上,所以k=﹣8×3=﹣24.
所以反比例函数的表达式为y=﹣.
(3)设直线BC的表达式为y=ax+c(a≠0).
将B(2,0),C(﹣8,3)代入,得解得
所以直线BC的表达式为y=﹣x+.所以P.所以AP=3.6.所以S△ABP=×3.6×2=3.6.
24.
解:(1)慢车速度为900÷12=75(km/h),则快车的速度为(900﹣75×4)÷4=150(km/h).
则s1=900﹣75x(0≤x≤12),s2=150x(0≤x≤6).
s1,s2与x之间的函数图象如图4所示.
(2)由(1)知s1=900﹣75x.当x=4.5时,s1=562.5.
设s3与x之间的函数关系式为s3=150x+b,
当x=4.5时,s3=562.5.则562.5=150×4.5+b,得b=﹣112.5.
所以s3=150x﹣112.5.
(3)令s3=150x﹣112.5=0,解得x=0.75.
所以第二列快车比第一列快车晚出发0.75小时.
6
函数及其图象测试题
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.
下列函数:①y=2x﹣1;②y=﹣;③y=;④y=x2.其中一次函数有( )
A.1个
B.2个
C.3个
D.4个
2.在平面直角坐标系中,若点A(-m,n)在第四象限,则点B(1-n,m)在( )
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
3.弹簧挂上物体后会伸长,测得一弹簧的长度y
(cm)与所挂物体的质量x(kg)之间有下面的关系:
x/kg
0
1
2
3
4
5
y/cm
20
20.5
21
21.5
22
22.5
下列说法不正确的是(
)
弹簧不挂重物时的长度为20
cm
x与y都是变量,
x是自变量,y是x的函数
物体质量每增加1
kg,弹簧的长度y增加0.5
cm
D.所挂物体质量为7
kg时,弹簧的长度为24
cm
4.要得到直线的图象,可以把直线(
)
A.向上平移4个单位长度
B.向下平移4个单位长度
C.向左平移4个单位长度
D.向右平移4个单位长度
5.已知直角坐标系中点P到y轴的距离为5,且点P到x轴的距离为3,则这样的点P的个数是(
)
A.1
B.2
C.3
D.4
6.
若一个正比例函数的图象经过不同象限的两点
A(m,-1)B(-5,n)则下列判断正确的是(
)
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0
7.
如图1,已知A为反比例函数y=(x<0)图象上一点,过点A作AB⊥y轴,垂足为B.若△OAB的面积为2,则k的值为( )
A.2
B.﹣2
C.4
D.﹣4
图1
图2
图3
图4
8.
如图2,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB长为半径画弧,交x轴正半轴于点C,则点C的坐标为( )
A.(,0)
B.(-2,0)
C.(2-,0)
D.(0,-2)
9.如图3,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A.设P点经过的路程为x,以点A,P,D为顶点的三角形的面积为y,则下列图象能大致反映y与x的函数关系的是( )
10.
某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S(吨)与时间t(小时)之间的函数关系如图4所示,这批物资从开始调进到全部调出需要的时间是( )
A.4小时
B.4.3小时
C.4.4小时
D.5小时
二、填空题(本大题共6小题,每小题3分,共18分)
11.如果点A(-2,a)在函数y=
-x+3的图象上,那么a的值等于________.
12.已知点(-4,y1),(-2,y2),(1,y3)都在直线y=-x+b上,则y1,y2,y3的值的大小关系是________.
13如图5,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),有以下说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.其中说法正确的是________.(填序号)
图5
图6
图7
写出一个一次函数的表达式,使它的图象与x轴的正半轴夹角为45°,这个一次函数的表达式是:
?.
如图6,定点A(-2,0),动点B在直线y=x上运动,当线段AB最短时,点B的坐标为
?.
16.如图7,A是反比例函数y=(k≠0)图象上一点,过点A作AB⊥y轴于点B,C,D为x轴上的动点,若CD=3AB,四边形ABCD的面积为4,则该反比例函数的表达式为________________.
三、解答题(本大题共7小题,共52分)
17.(6分)如图8,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,求这个一次函数的表达式.
图8
18.(6分)已知反比例函数y=(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个反比例函数的表达式;
(2)判断点B(﹣1,6),C(3,2)是否在反比例函数的图象上,并说明理由;
(3)当﹣3<x<﹣1时,求y的取值范围.
19.(6分)某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.图9是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问:这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
图9
20.(8分)已知一次函数y=-2x-2.
(1)根据关系式在图10中画出函数的图象;
(2)求出图象与x轴,y轴的交点A,B的坐标;
(3)求A,B两点间的距离.
(4)y的值随x值的增大怎样变化?
图10
图11
21.(8分)甲、乙两车同时从A地出发驶向B地.甲车到达B地后立即返回,设甲车离A地的距离为y1(千米),乙车离A地的距离为y2(千米),行驶时间为x(小时),y1,y2与x的函数关系如图11所示.
(1)填空:A,B两地相距______千米,甲车从B地返回A地的行驶速度是______千米/时;
(2)当两车行驶7小时后在途中相遇,求点E的坐标;
(3)甲车从B地返回A地途中,与乙车相距100千米时,求甲车行驶的时间.
22.(8分)如图12,在平面直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,写出点C的坐标;
(3)点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
图12
图13
23.
(10分)如图13,已知直线AB分别交x轴和y轴与B、A两点,A(0,﹣3),B(2,0).
(1)求直线AB的表达式;
(2)将线段AB平移至DC的位置,其点D在x轴的负半轴上,点C在反比例函数y=的图象上,若S△BCD=18,求反比例函数的表达式;
(3)设BC交y轴于点P,求S△ABP.
附加题(20分,不计入总分)
24.【原题重现】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图14中的折线表示y与x之间的函数关系.
……
若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
【问题再研】
若设慢车行驶的时间为x(h),慢车与甲地的距离为s1(km),第一列快车与甲地的距离为s2(km),第二列快车与甲地的距离为s3(km),根据原题中所给信息解决下列问题:
(1)在同一直角坐标系中,分别画出s1,s2与x之间的函数图象;
(2)求s3与x之间的函数关系式;
(3)求原题的答案.
图14
第17章
函数及其图象测试题
一、1.
B
2.D
3.
D
4.
B
5.
D
6.
A
7.
D
8.
B
9.
A
10.
C
10.
C
提示:由图中可以看出,2小时调进物资3吨,调进物资共用4小时,即物资一共有6吨;2小时后,调进物资和调出物资同时进行,4小时时,物资调进完毕,仓库还剩1吨,说明调出的速度为(6-1)÷2=2.5(吨/时),调出所需时间为6÷2.5=2.4(小时),所以一共的时间是2+2.4=4.4(小时).
二、11.
4
12.
y1>y2>y3
13.
①②③
14.
答案不唯一,如y=-x+1
15.(-1,-1)
16.
三、17.
解:因为点B在正比例函数y=2x的图象上,横坐标为1,所以y=2×1=2.所以B(1,2).
设一次函数的表达式为y=kx+b.将A(0,3),B(1,2)代入,得b=3,k+b=2,解得k=-1.
所以这个一次函数的表达式为y=﹣x+3.
18.
(1)y=.
(2)B(﹣1,6)不在反比例函数的图象上,C(3,2)在反比例函数的图象上.理由略.
(3)﹣6<y<﹣2.
19.
解:(1)
(2)由(1)知恒温系统设定恒温为20°C.
(3)把y=10代入y=
中,解得x=20.20-10=10(小时).
答:恒温系统最多关闭10小时,蔬菜才能避免受到伤害
20.
解:(1)在y=-2x-2中,令y=0,可得x=-1;令x=0,可得y=-2.
所以图象是过(-1,0)和(0,-2)的一条直线,其图象如图1所示.
(2)由(1)可知A(-1,0),B(0,-2).
(3)因为A(-1,0),B(0,-2),所以OA=1,OB=2.所以AB==,即A,B两点间的距离为.
(4)因为在y=-2x-2中,k=-2<0,所以y随x的增大而减小.
21.
解:(1)800
100
(2)乙车行驶的时间为7小时,行驶的路程为800-100×(7-6)=700,所以E(7,700).
(3)设相遇前经过x小时甲、乙两车相距100千米.
则有100x+100+100(x-6)=800,解得x=6.5;
设相遇后经过x小时,甲、乙两车相距100千米.
则有100x+100(x-6)-100=800,解得x=7.5.
所以甲车行驶的时间是6.5小时或7.5小时时,两车相距100千米.
22.
解:(1)将点A(2,0)代入y=kx+3,得0=2k+3,解得k=
-.
所以y=
-x+3.
当x=0时,y=3.所以B(0,3),OB=3.
当y=0时,-x+3=0,解得x=2.
所以A(2,0),OA=2.
所以S△AOB=OA?OB=×2×3=3.
(2)如图2,①当AB=BC时,点C与点A(2,0)关于y轴对称,所以C(-2,0);
②当AB=AC时,由OA=2,OB=3,得AB==,由AB=AC′=AC″=,得C′(+2,0),C″(-2,0).
综上所述,符合条件的点C的坐标是(-2,0),(+2,0)或(-2,0).
图2
图3
图4
(3)因为M(0,3),所以OM=3.所以AM=3-2=1.由(1)知,S△AOB=3,所以S△PBM=S△AOB=3.
①如图3,当点P在x轴下方时,S△PBM=S△ABM+S△APM=+?AM?|yP|=+×1×|yP|=3.所以|yP|=3.
因为点P在x轴下方,所以yP=-3.将y=-3代入y=-x+3,得-3=-x+3,解得x=4.所以P(4,-3);
②如图3,当点P在x轴上方时,S△PBM=S△PAM-S△ABM=?AM?|yP|-=×1×|yP|-=3.所以|yP|=9.
因为点P在x轴上方,所以yP=9.将y=9代入y=-x+3,得9=
-x+3,解得x=-4.所以P(-4,9).
23.
解:(1)设直线AB的表达式为y=kx+b(k≠0).
将A(0,﹣3),B(2,0)代入,得解得
所以直线AB的表达式为y=x﹣3.
(2)由A(0,﹣3),B(2,0),将线段AB平移至DC的位置,得D(xD,0),C(xD+2,3).
又因为S△BCD=BD×3=18,所以|(xD﹣2)|×3=18.所以xD=﹣10.
所以D(﹣10,0),C(﹣8,3).
因为点C在反比例函数y=的图象上,所以k=﹣8×3=﹣24.
所以反比例函数的表达式为y=﹣.
(3)设直线BC的表达式为y=ax+c(a≠0).
将B(2,0),C(﹣8,3)代入,得解得
所以直线BC的表达式为y=﹣x+.所以P.所以AP=3.6.所以S△ABP=×3.6×2=3.6.
24.
解:(1)慢车速度为900÷12=75(km/h),则快车的速度为(900﹣75×4)÷4=150(km/h).
则s1=900﹣75x(0≤x≤12),s2=150x(0≤x≤6).
s1,s2与x之间的函数图象如图4所示.
(2)由(1)知s1=900﹣75x.当x=4.5时,s1=562.5.
设s3与x之间的函数关系式为s3=150x+b,
当x=4.5时,s3=562.5.则562.5=150×4.5+b,得b=﹣112.5.
所以s3=150x﹣112.5.
(3)令s3=150x﹣112.5=0,解得x=0.75.
所以第二列快车比第一列快车晚出发0.75小时.
6
