2020-2021学年 高一物理 平抛运动的规律及应用 强化学案Word版含答案
文档属性
| 名称 | 2020-2021学年 高一物理 平抛运动的规律及应用 强化学案Word版含答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 753.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-14 13:12:34 | ||
图片预览




文档简介
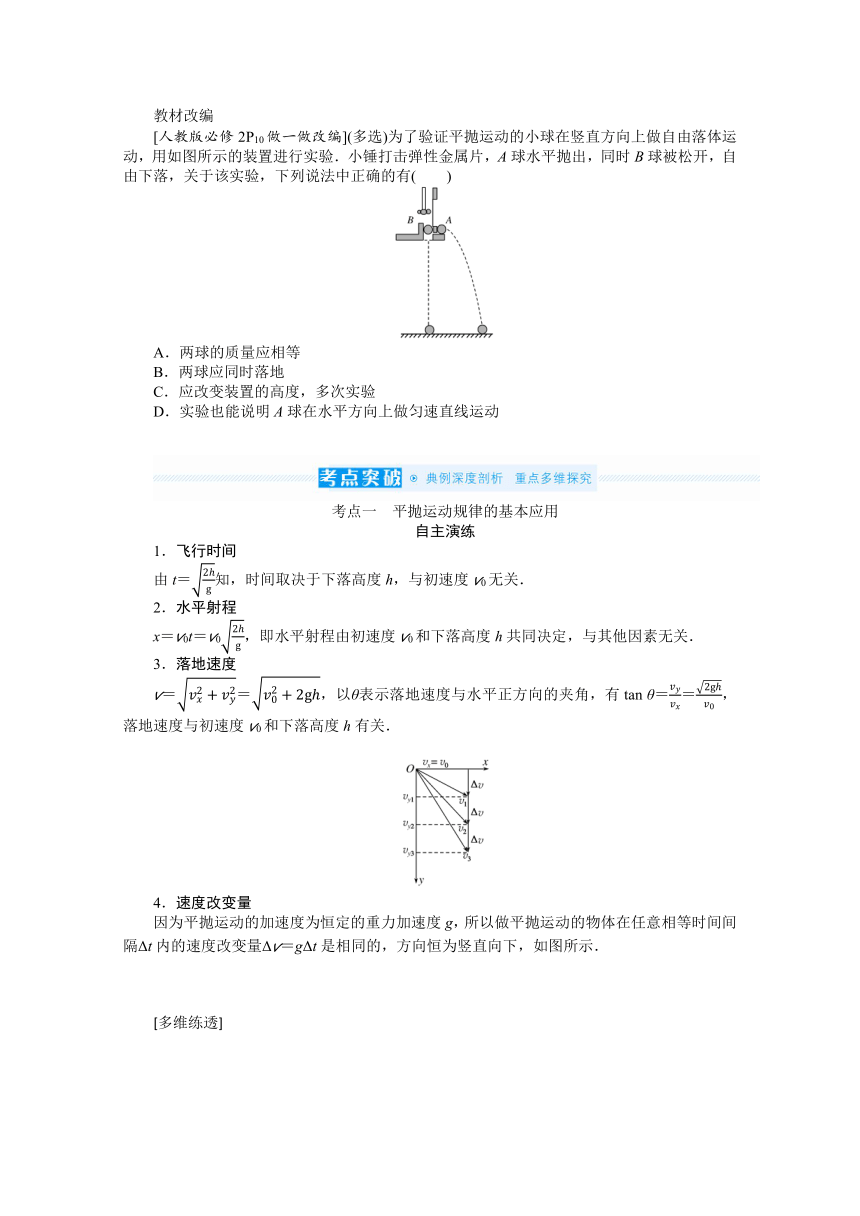
平抛运动的规律及应用
知识点一 平抛运动
1.定义:将物体以一定的初速度沿水平方向抛出,物体只在________作用下的运动.
2.性质:平抛运动是加速度为g的________曲线运动,运动轨迹是抛物线.
3.研究方法:运动的合成与分解.
(1)水平方向:________直线运动;
(2)竖直方向:________运动.
4.基本规律:(如下图)
(1)位移关系
(2)速度关系
知识点二 斜抛运动
1.定义:将物体以初速度v0________或斜向下方抛出,
物体只在________作用下的运动.如图所示.
2.性质:斜抛运动是加速度为g的________曲线运动,
运动轨迹是________.
3.研究方法:运动的合成与分解
(1)水平方向:________直线运动;
(2)竖直方向:________直线运动.
思考辨析
(1)平抛运动属于匀变速曲线运动.( )
(2)平抛运动的加速度方向时刻在变化.( )
(3)做平抛运动的物体在任意时刻的速度方向与水平方向的夹角保持不变.( )
(4)做平抛运动的物体在任意相等的两段时间内的速度变化相同.( )
教材改编
[人教版必修2P10做一做改编](多选)为了验证平抛运动的小球在竖直方向上做自由落体运动,用如图所示的装置进行实验.小锤打击弹性金属片,A球水平抛出,同时B球被松开,自由下落,关于该实验,下列说法中正确的有( )
A.两球的质量应相等
B.两球应同时落地
C.应改变装置的高度,多次实验
D.实验也能说明A球在水平方向上做匀速直线运动
考点一 平抛运动规律的基本应用
自主演练
1.飞行时间
由t=2hg知,时间取决于下落高度h,与初速度v0无关.
2.水平射程
x=v0t=v02hg,即水平射程由初速度v0和下落高度h共同决定,与其他因素无关.
3.落地速度
v=vx2+vy2=v02+2gh,以θ表示落地速度与水平正方向的夹角,有tan θ=vyvx=2ghv0,落地速度与初速度v0和下落高度h有关.
4.速度改变量
因为平抛运动的加速度为恒定的重力加速度g,所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt是相同的,方向恒为竖直向下,如图所示.
[多维练透]
1.(多选)如图所示,水平地面上有一个坑,其竖直截面为正方形ABCD,若在A点以初速度v0沿AB方向抛出一小球,小球会击中坑壁上的C点,已知AB的长度为l,忽略空气阻力,则( )
A.小球下落的时间t=lv0
B.坑的深度AD=gl22v02
C.落到C点的速度大小为2v0
D.落到C点时速度方向与水平成60°角
2.[2020·全国卷Ⅱ,16]如图,在摩托车越野赛途中的水平路段前方有一个坑,该坑沿摩托车前进方向的水平宽度为3h,其左边缘a点比右边缘b点高0.5h.若摩托车经过a点时的动能为E1,它会落到坑内c点,c与a的水平距离和高度差均为h;若经过a点时的动能为E2,该摩托车恰能越过坑到达b点. E2E1等于( )
A.20 B.18 C.9.0 D.3.0
3. [2020·江苏卷,8](多选)如图所示,小球A、B分别从2l和l的高度水平抛出后落地,上述过程中A、B的水平位移分别为l和2l.忽略空气阻力,则( )
A.A和B的位移大小相等
B.A的运动时间是B的2倍
C.A的初速度是B的12
D.A的末速度比B的大
4.[2020·北京卷,17]无人机在距离水平地面高度h处,以速度v0水平匀速飞行并释放一包裹,不计空气阻力,重力加速度为g.
(1)求包裹释放点到落地点的水平距离x;
(2)求包裹落地时的速度大小v;
(3)以释放点为坐标原点,初速度方向为x轴方向,竖直向下为y轴方向,建立平面直角坐标系,写出该包裹运动的轨迹方程.
考点二 平抛运动的综合问题
多维探究
题型1平抛运动重要推论的应用
两个重要推论
(1)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示,即xB=xA2
(2)做平抛运动的物体在任意时刻任意位置处,有tan θ=2tan α.
例1 [2021·安徽太和中学月考]如图所示,xOy是平面直角坐标系,Ox水平、Oy竖直,一质点从O点开始做平抛运动,P点是轨迹上的一点.质点在P点的速度大小为v,方向沿该点所在轨迹的切线.M点为P点在Ox轴上的投影,P点速度方向的反向延长线与Ox轴相交于Q点.已知平抛的初速度大小为20 m/s,MP=20 m,重力加速度g取10 m/s2,则下列说法正确的是( )
A.QM的长度为10 m
B.质点从O点到P点的运动时间为1 s
C.质点在P点的速度大小v为40 m/s
D.质点在P点的速度方向与水平方向的夹角为45°
题型2|逆向思维和对称方法的应用
例2 (多选)如图所示,假设某人在高度H=5 m的竖直杆左侧用弹弓将一弹丸从A点发射出去,弹丸刚好从竖直杆BN顶端B点以v=10 m/s的水平速度通过后,落到水平地面上的C点.已知弹丸质量m=50 g,A点到水平地面高度h=1.8 m,不计空气阻力,g取10 m/s2.下列说法正确的是( )
A.N、C之间的距离x=12 m
B.A点到竖直杆的水平距离为8 m
C.弹丸落地时的速度大小为102m/s
D.弹弓对弹丸做的功为4.2 J
题型3 平抛运动的临界极值问题
例3 如图所示,滑板运动员从倾角为53°的斜坡顶端距水平地面高度H=3.2 m的A点水平滑出,斜面底端有个宽L=1.2 m、高h=1.4 m的障碍物.忽略空气阻力,重力加速度g取10 m/s2,sin 53°=0.8,cos 53°=0.6.为了不触及这个障碍物并落在水平面上,运动员从A点沿水平方向滑出的最小速度为( )
A.3.0 m/s B.4.0 m/s C.4.5 m/s D.6.0 m/s
练1 [2020·浙江温州九校联考]
在第18届亚运会,中国女排毫无悬念地赢得了冠军,图为中国队员比赛中高抛发球.若排球离开手时正好在底线中点正上空3.49 m处,速度方向水平且与底线垂直.已知每边球场的长和宽均9 m,球网高2.24 m,不计空气阻力,g取10 m/s2.为了使球能落到对方场地,下列发球速度大小可行的是( )
A.15 m/s B.17 m/s C.20 m/s D.25 m/s
练2 [2020·河北石家庄5月模拟]
如图,容量足够大的圆筒竖直放置,水面高度为h,在圆筒侧壁开一个小孔P,筒内的水从小孔水平射出,设水到达地面时的落点距小孔的水平距离为x,小孔P到水面的距离为y.短时间内可认为筒内水位不变,重力加速度大小为g,不计空气阻力,在这段时间内,下列说法正确的是( )
A.水从小孔P射出的速度大小为gy
B.y越小,则x越大
C.x与小孔P的位置无关
D.当y=h2时,x最大,最大值为h
题后反思
平抛运动中临界问题的分析方法
思维拓展
四种典型落点位置的平抛运动
类型1 落点在水平面上
例1 [2021·宁波十校联考]如图所示为乒乓球桌面示意图,球网上沿高出桌面h,网到桌边的水平距离为L.在某次乒乓球训练中,从桌面左侧距网水平距离为12L处,将球沿垂直于网的方向以速度v水平击出,球恰好通过网的上沿并落到桌面右侧边缘.将乒乓球的运动看成平抛运动,下列判断正确的是( )
A.击球点离桌面的高度与网高度之比为2:1
B.乒乓球在网的左、右两侧运动时间之比为1:3
C.乒乓球过网时与落到右侧桌边缘时的速率之比为1:3
D.乒乓球在网左、右两侧速度变化量之比为1:2
类型2 落点在斜面上
例2 [2021·浙江名校联考]如图(a)是研究小球在斜面上平抛运动的实验装置,每次将小球从弧型轨道同一位置静止释放,并逐渐改变斜面与水平地面之间的夹角θ,获得不同的射程x,最后作出了如图(b)所示的x?tan θ图象,重力加速度g取10 m/s2.下列说法正确的是( )
A.由图(b)可知,小球在斜面顶端水平抛出时的初速度大小v0=5 m/s
B.由题中所给条件无法求出小球在斜面顶端水平抛出时的初速度大小
C.若最后得到的图象如图(c)所示,可能是由于小球释放位置降低造成的
D.若实验中发现当θ=60°时,小球恰好落在斜面底端,则斜面的长度L=235 m
题后反思
解决斜面约束下的平抛运动问题时要抓住几何关系,灵活应用各种规律,特别要注意速度偏向角和位移偏向角的关系.若质点从斜面外抛出,垂直落在斜面上,则有tan θ=v0gt,解得t=v0gtan θ,以上两式中的θ为斜面倾角.
类型3 落点在竖直面上
例3 [2020·浙江衢州、湖州、丽水三市4月质检]如图所示,网球发球机水平放置在水平地面上方某处,正对着竖直墙面发射网球,两次发射的两球分别在墙上留下A、B两点印迹,测得OA=AB=h.OP为水平线,若忽略网球在空中受到的阻力,则( )
A.两球发射的初速度之比vOA:vOB=2:1
B.两球碰到墙面瞬间运动的时间之比tA:tB=1:2
C.两球碰到墙面时的动量可能相同
D.两球碰到墙面时的动能可能相等
类型4 落点在曲面上
例4 [2021·江苏淮安四校联考]如图,可视为质点的小球,位于半径为3 m的半圆柱体左端点A的正上方某处,以初速度大小v0水平抛出一小球,其运动轨迹恰好能与半圆柱体相切于B点.过B点的半圆柱体半径与水平方向的夹角为60°,取g=10 m/s2,不计空气阻力,则初速度大小为( )
A. 553 m/s B.43 m/s C.35 m/s D. 152 m/s
练1 [2021·株洲模拟](多选)将一小球以水平速度v0=10 m/s从O点向右抛出,经3 s小球恰好垂直落到斜面上的A点,不计空气阻力,g取10 m/s2,B点是小球做自由落体运动在斜面上的落点,如图所示,以下判断正确的是( )
A.斜面的倾角是30°
B.小球的抛出点距斜面上B点的竖直高度是15 m
C.若将小球以水平速度v′0=5 m/s向右抛出,它一定落在AB的中点P的上方
D.若将小球以水平速度v′0=5 m/s向右抛出,它一定落在AB的中点P处
练2 (多选)如图所示,a、b两小球(均可视为质点)分别从直径在水平线上的半圆轨道右端和足够长的斜面轨道顶端以大小相等的初速度同时由同一高度水平抛出,且同时落到各自轨道上.已知半圆轨道的半径为103 m,斜面轨道的倾角θ=30°,取g=10 m/s2,不计空气阻力,则( )
A.两小球抛出时的速度大小为10 m/s
B.两小球抛出时的速度大小为15 m/s
C.两小球在空中的运动时间为3 s
D.两小球在空中的运动时间为1.5 s
题后反思
有约束条件的平抛运动解题策略
第2讲 平抛运动的规律及应用
基础落实
知识点一
1.重力
2.匀变速
3.(1)匀速 (2)自由落体
4.(1)v0t 12gt2 x2+y2 gt2v0
(2)v0 gt vx2+vy2 gtv0
知识点二
1.斜向上方 重力
2.匀变速 抛物线
3.(1)匀速 (2)匀变速
思考辨析
(1)√ (2)× (3)× (4)√
教材改编
解析:根据合运动与分运动的等时性和独立性特点可知,两球应同时落地,为减小实验误差,应改变装置的高度,多次做实验,选项B、C正确;平抛运动的实验与小球的质量无关,选项A错误;此实验只能说明A球在竖直方向做自由落体运动,选项D错误.
答案:BC
考点突破
1.解析:小球做平抛运动的水平位移l=v0t,则小球下落的时间为t=lv0,A项正确;小球在竖直方向的位移y=12gt2=gl22v02 ,B正确;落到C点时,水平分位移与竖直分位移大小相等,即v0t=vy2t,所以vy=2v0,落到C点的速度v=v02+vy2 =5v0,方向为tan θ=vyv0=2,不等于60°,C、D两项错误.
答案:AB
2.解析:由平抛运动规律有x=v0t,y=12gt2,得v0=xg2y;动能Ek=12mv02=mgx24y∝x2y,故E2E1=x2x12·y1y2=3hh2·h0.5h=18,故B正确.
答案:B
3.解析:由题意可知,落地后,小球A的位移的大小为sA=xA2+yA2 =l2+2l2=5l,小球B的位移的大小为sB=xB2+yB2 =2l2+l2=5l,显然小球A、B的位移大小相等,A正确;小球A的运动时间为tA= 2yAg=4lg,小球B的运动时间为tB= 2yBg=2lg,则tA∶tB=2∶1,B错误;小球A的初速度为vxA=xAtA=l4lg=gl4,小球B的初速度为vxB=xBtB=2l2lg=2gl,则vA∶vB=1∶22,C错误;落地瞬间,小球A竖直方向的速度为vyA=4gl,小球B竖直方向的速度为vyB=2gl,则落地瞬间小球A的速度为vA=vxA2+vyA2 = 174gl,小球B的速度为vB=vxB2+vyB2 =4gl,显然vA>vB,D正确.
答案:AD
4.解析:(1)包裹脱离无人机后做平抛运动,在竖直方向做自由落体运动,则h=12gt2
解得t=2hg
水平方向上做匀速直线运动,所以水平距离为
x=v0t=v02hg
(2)包裹落地时,竖直方向速度为
vy=gt=g2hg
落地时速度为v=v02+vy2=v02 +2gh
(3)包裹做平抛运动,分解位移
x=v0t′
y=12gt′2
两式消去时间得包裹的轨迹方程为y=g2v02 x2
答案:1v02hg 2v02+2gh (3)y=g2v02 x2
例1 解析:由h=12gt2得,质点从O点到P点的运动时间为t=2 s,B错误;由tan θ=vyv0=gtv0=gt2v0t=2hx,质点在水平方向的位移为x=v0t=40 m,故Q是OM的中点,QM=20 m,A错误;质点在P点的速度大小为v=v02+vy2 =202 m/s,C错误;tan θ=vyv0=1,故质点在P点的速度方向与水平方向的夹角为45°,D正确.
答案:D
例2 解析:弹丸越过B点后做平抛运动,在竖直方向上有H=12gt2,水平方向上有x=vt,联立解得N、C之间的距离x=10 m,选项A错误;把弹丸从A点到B点的斜抛运动看成逆向的从B点到A点的平抛运动(逆向思维法),在竖直方向上有H-h=12gt′2,解得弹丸从A点运动B点的时间t′=0.8 s,则A点到竖直杆的水平距离x′=vt′=8 m,选项B正确;弹丸从B点运动到C点,由机械能守恒定律有mgH+12mv2=12mvC2,解得弹丸落地时的速度大小为vC=102 m/s,选项C正确;整个运动过程中,由功能关系得W=12mvC2-mgh,解得弹弓对弹丸做的功为W=4.1 J,选项D错误.
答案:BC
例3 解析:由题意,可知要使运动员不触及障碍物,则运动员下落到与障碍物等高时,根据几何关系可知运动员在水平方向发生的位移应该满足:x≥Htan53°+L
此时运动员在竖直方向下落的高度为H-h,设运动员运动的时间为t,则有:
H-h=12gt2
代入数据可得时间为:t=0.6 s
所以运动员从A点沿水平方向滑出的最小速度为:
vmin=6 m/s,故D正确,A、B、C错误.
答案:D
练1 解析:本题实质为平抛运动的临界问题.设排球离开手时的高度为H,网高为h,每边球场的长和宽均为L,排球刚好过网时,由平抛运动规律可知,在竖直方向H-h=12gt12 ,在水平方向L=v1t1,解得v1=18 m/s.排球刚好落到对方的场地的底线时,由平抛运动公式有,在竖直方向H=12gt22,在水平方向2L=v2t2,解得v2≈21.5 m/s,所以要使球落在对方场地,发球速度范围为18 m/s≤v≤21.5 m/s,故C符合要求.
答案:C
练2 解析:取水面上质量为m的水滴,从小孔P射出时由机械能守恒定律有mgy=12mv2,解得v=2gy,选项A错误;水从小孔P射出时做平抛运动,则x=vt,h-y=12gt2,解得x=2yh-y,可见x与小孔P的位置有关,因y+(h-y)=h为定值,由数学关系可知,当y=h-y,即y=12h时x最大,最大值为h,并不是y越小,x越大,选项D正确,B、C均错误.
答案:D
思维拓展
典例1 解析:设击球点高出桌面H,乒乓球在网的左、右两侧运动时间分别为t1、t2,乒乓球做平抛运动,经时间t在水平方向上的位移x=vt,在竖直方向上的位移y=12gt2,即t∝x,y∝t2,则t1t2=L2L,H-hH=t1t1+t22,整理得t1∶t2=1∶2,H∶h=9∶8,选项A、B错误;由加速度的定义式得g=Δv1t1,g=Δv2t2,则乒乓球在网的左、右两侧速度变化量之比Δv1∶Δv2=t1∶t2=1∶2,选项D正确;根据机械能守恒定律得12mv12 =mgH-h+12mv2,12mv22=mgH+12mv2,则乒乓球过网时与落到右侧桌边缘时的速率之比v1v2=v2+2gH-hv2+2gH=v2+2g·H9v2+2gH≠ 2g·H92gH=13,选项C错误.
答案:D
典例2 解析:小球在空中做平抛运动,在竖直方向上有y=12gt2,水平方向上有x=v0t,由几何关系有yx=tan θ,解得x=2v02 gtan θ,由图(b)可知2v02 g=0.10.5,解得小球在斜面顶端水平抛出时的初速度大小v0=1 m/s,选项A、B错误;由图(c)可知,图象末端的斜率增大,说明2v02 g增大,又重力加速度不变,可知做平抛运动的初速度增大,其原因可能为小球在弧形轨道上的释放位置变高或小球释放时有初速度,选项C错误;当θ=60°时,水平位移大小x=2×1210tan 60° m=35 m,由于小球恰好落在斜面底端,则斜面长度L=xcosθ=235 m,选项D正确.
答案:D
典例3 解析:忽略空气阻力,网球做的运动可视为平抛运动,在竖直方向上有h=12gtA2,2h=12gtB2,解得tA∶tB=1∶2,在水平方向上有x=vOAtA,x=vOBtB,则vOA∶vOB=2∶1,A、B均错误;动量为矢量,由图可知,二者与墙碰撞时其速度方向不相同,故二者碰到墙面时的动量不可能相同,C错误;由排除法知选项D正确(从抛出到与墙碰撞的过程中,根据机械能守恒定律有EkA=mgh+12mvOA2,EkB=mg·2h+12mvOB2,可得EkB-EkA=mgh+12mvOB2-12mvOA2=m2(2gh-vOB2),由数学知识可知,当vOB=2gh时,有EkA=EkB,D正确.
答案:D
典例4 解析:将小球到达B点时的速度沿水平方向和竖直方向分解,则vy=gt,R+R cos 60°=v0t,由几何关系得v0vy=tan 60°,解得v0=35 m/s,选项C正确.
答案:C
练1 解析:设斜面倾角为θ,对小球在A点的速度进行分解有tan θ=v0gt,解得θ=30°,A项正确;小球距过A点水平面的距离为h=12gt2=15 m,所以小球的抛出点距斜面上B点的竖直高度肯定大于15 m,B项错误;若小球的初速度为v′0=5 m/s,过A点作水平面,小球落到水平面的水平位移是小球以初速度v0=10 m/s抛出时的一半,延长小球运动的轨迹线,得到小球应该落在P、A之间,C项正确,D项错误.
答案:AC
练2 解析:两小球做平抛运动具有对称性,把左侧半圆对称到右侧,小球的落点为斜面与右侧半圆的交点,如图所示.由几何关系可知,小球落到斜面上时,在水平方向上有x=v0t,竖直方向上有y=12gt2,由几何关系得y=r sin 2θ,yx=tan θ,解得两小球抛出时的速度大小为v0=15 m/s,两小球在空中的运动时间为t=3 s,选项B、C均正确,A、D均错误.
答案:BC
知识点一 平抛运动
1.定义:将物体以一定的初速度沿水平方向抛出,物体只在________作用下的运动.
2.性质:平抛运动是加速度为g的________曲线运动,运动轨迹是抛物线.
3.研究方法:运动的合成与分解.
(1)水平方向:________直线运动;
(2)竖直方向:________运动.
4.基本规律:(如下图)
(1)位移关系
(2)速度关系
知识点二 斜抛运动
1.定义:将物体以初速度v0________或斜向下方抛出,
物体只在________作用下的运动.如图所示.
2.性质:斜抛运动是加速度为g的________曲线运动,
运动轨迹是________.
3.研究方法:运动的合成与分解
(1)水平方向:________直线运动;
(2)竖直方向:________直线运动.
思考辨析
(1)平抛运动属于匀变速曲线运动.( )
(2)平抛运动的加速度方向时刻在变化.( )
(3)做平抛运动的物体在任意时刻的速度方向与水平方向的夹角保持不变.( )
(4)做平抛运动的物体在任意相等的两段时间内的速度变化相同.( )
教材改编
[人教版必修2P10做一做改编](多选)为了验证平抛运动的小球在竖直方向上做自由落体运动,用如图所示的装置进行实验.小锤打击弹性金属片,A球水平抛出,同时B球被松开,自由下落,关于该实验,下列说法中正确的有( )
A.两球的质量应相等
B.两球应同时落地
C.应改变装置的高度,多次实验
D.实验也能说明A球在水平方向上做匀速直线运动
考点一 平抛运动规律的基本应用
自主演练
1.飞行时间
由t=2hg知,时间取决于下落高度h,与初速度v0无关.
2.水平射程
x=v0t=v02hg,即水平射程由初速度v0和下落高度h共同决定,与其他因素无关.
3.落地速度
v=vx2+vy2=v02+2gh,以θ表示落地速度与水平正方向的夹角,有tan θ=vyvx=2ghv0,落地速度与初速度v0和下落高度h有关.
4.速度改变量
因为平抛运动的加速度为恒定的重力加速度g,所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv=gΔt是相同的,方向恒为竖直向下,如图所示.
[多维练透]
1.(多选)如图所示,水平地面上有一个坑,其竖直截面为正方形ABCD,若在A点以初速度v0沿AB方向抛出一小球,小球会击中坑壁上的C点,已知AB的长度为l,忽略空气阻力,则( )
A.小球下落的时间t=lv0
B.坑的深度AD=gl22v02
C.落到C点的速度大小为2v0
D.落到C点时速度方向与水平成60°角
2.[2020·全国卷Ⅱ,16]如图,在摩托车越野赛途中的水平路段前方有一个坑,该坑沿摩托车前进方向的水平宽度为3h,其左边缘a点比右边缘b点高0.5h.若摩托车经过a点时的动能为E1,它会落到坑内c点,c与a的水平距离和高度差均为h;若经过a点时的动能为E2,该摩托车恰能越过坑到达b点. E2E1等于( )
A.20 B.18 C.9.0 D.3.0
3. [2020·江苏卷,8](多选)如图所示,小球A、B分别从2l和l的高度水平抛出后落地,上述过程中A、B的水平位移分别为l和2l.忽略空气阻力,则( )
A.A和B的位移大小相等
B.A的运动时间是B的2倍
C.A的初速度是B的12
D.A的末速度比B的大
4.[2020·北京卷,17]无人机在距离水平地面高度h处,以速度v0水平匀速飞行并释放一包裹,不计空气阻力,重力加速度为g.
(1)求包裹释放点到落地点的水平距离x;
(2)求包裹落地时的速度大小v;
(3)以释放点为坐标原点,初速度方向为x轴方向,竖直向下为y轴方向,建立平面直角坐标系,写出该包裹运动的轨迹方程.
考点二 平抛运动的综合问题
多维探究
题型1平抛运动重要推论的应用
两个重要推论
(1)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图所示,即xB=xA2
(2)做平抛运动的物体在任意时刻任意位置处,有tan θ=2tan α.
例1 [2021·安徽太和中学月考]如图所示,xOy是平面直角坐标系,Ox水平、Oy竖直,一质点从O点开始做平抛运动,P点是轨迹上的一点.质点在P点的速度大小为v,方向沿该点所在轨迹的切线.M点为P点在Ox轴上的投影,P点速度方向的反向延长线与Ox轴相交于Q点.已知平抛的初速度大小为20 m/s,MP=20 m,重力加速度g取10 m/s2,则下列说法正确的是( )
A.QM的长度为10 m
B.质点从O点到P点的运动时间为1 s
C.质点在P点的速度大小v为40 m/s
D.质点在P点的速度方向与水平方向的夹角为45°
题型2|逆向思维和对称方法的应用
例2 (多选)如图所示,假设某人在高度H=5 m的竖直杆左侧用弹弓将一弹丸从A点发射出去,弹丸刚好从竖直杆BN顶端B点以v=10 m/s的水平速度通过后,落到水平地面上的C点.已知弹丸质量m=50 g,A点到水平地面高度h=1.8 m,不计空气阻力,g取10 m/s2.下列说法正确的是( )
A.N、C之间的距离x=12 m
B.A点到竖直杆的水平距离为8 m
C.弹丸落地时的速度大小为102m/s
D.弹弓对弹丸做的功为4.2 J
题型3 平抛运动的临界极值问题
例3 如图所示,滑板运动员从倾角为53°的斜坡顶端距水平地面高度H=3.2 m的A点水平滑出,斜面底端有个宽L=1.2 m、高h=1.4 m的障碍物.忽略空气阻力,重力加速度g取10 m/s2,sin 53°=0.8,cos 53°=0.6.为了不触及这个障碍物并落在水平面上,运动员从A点沿水平方向滑出的最小速度为( )
A.3.0 m/s B.4.0 m/s C.4.5 m/s D.6.0 m/s
练1 [2020·浙江温州九校联考]
在第18届亚运会,中国女排毫无悬念地赢得了冠军,图为中国队员比赛中高抛发球.若排球离开手时正好在底线中点正上空3.49 m处,速度方向水平且与底线垂直.已知每边球场的长和宽均9 m,球网高2.24 m,不计空气阻力,g取10 m/s2.为了使球能落到对方场地,下列发球速度大小可行的是( )
A.15 m/s B.17 m/s C.20 m/s D.25 m/s
练2 [2020·河北石家庄5月模拟]
如图,容量足够大的圆筒竖直放置,水面高度为h,在圆筒侧壁开一个小孔P,筒内的水从小孔水平射出,设水到达地面时的落点距小孔的水平距离为x,小孔P到水面的距离为y.短时间内可认为筒内水位不变,重力加速度大小为g,不计空气阻力,在这段时间内,下列说法正确的是( )
A.水从小孔P射出的速度大小为gy
B.y越小,则x越大
C.x与小孔P的位置无关
D.当y=h2时,x最大,最大值为h
题后反思
平抛运动中临界问题的分析方法
思维拓展
四种典型落点位置的平抛运动
类型1 落点在水平面上
例1 [2021·宁波十校联考]如图所示为乒乓球桌面示意图,球网上沿高出桌面h,网到桌边的水平距离为L.在某次乒乓球训练中,从桌面左侧距网水平距离为12L处,将球沿垂直于网的方向以速度v水平击出,球恰好通过网的上沿并落到桌面右侧边缘.将乒乓球的运动看成平抛运动,下列判断正确的是( )
A.击球点离桌面的高度与网高度之比为2:1
B.乒乓球在网的左、右两侧运动时间之比为1:3
C.乒乓球过网时与落到右侧桌边缘时的速率之比为1:3
D.乒乓球在网左、右两侧速度变化量之比为1:2
类型2 落点在斜面上
例2 [2021·浙江名校联考]如图(a)是研究小球在斜面上平抛运动的实验装置,每次将小球从弧型轨道同一位置静止释放,并逐渐改变斜面与水平地面之间的夹角θ,获得不同的射程x,最后作出了如图(b)所示的x?tan θ图象,重力加速度g取10 m/s2.下列说法正确的是( )
A.由图(b)可知,小球在斜面顶端水平抛出时的初速度大小v0=5 m/s
B.由题中所给条件无法求出小球在斜面顶端水平抛出时的初速度大小
C.若最后得到的图象如图(c)所示,可能是由于小球释放位置降低造成的
D.若实验中发现当θ=60°时,小球恰好落在斜面底端,则斜面的长度L=235 m
题后反思
解决斜面约束下的平抛运动问题时要抓住几何关系,灵活应用各种规律,特别要注意速度偏向角和位移偏向角的关系.若质点从斜面外抛出,垂直落在斜面上,则有tan θ=v0gt,解得t=v0gtan θ,以上两式中的θ为斜面倾角.
类型3 落点在竖直面上
例3 [2020·浙江衢州、湖州、丽水三市4月质检]如图所示,网球发球机水平放置在水平地面上方某处,正对着竖直墙面发射网球,两次发射的两球分别在墙上留下A、B两点印迹,测得OA=AB=h.OP为水平线,若忽略网球在空中受到的阻力,则( )
A.两球发射的初速度之比vOA:vOB=2:1
B.两球碰到墙面瞬间运动的时间之比tA:tB=1:2
C.两球碰到墙面时的动量可能相同
D.两球碰到墙面时的动能可能相等
类型4 落点在曲面上
例4 [2021·江苏淮安四校联考]如图,可视为质点的小球,位于半径为3 m的半圆柱体左端点A的正上方某处,以初速度大小v0水平抛出一小球,其运动轨迹恰好能与半圆柱体相切于B点.过B点的半圆柱体半径与水平方向的夹角为60°,取g=10 m/s2,不计空气阻力,则初速度大小为( )
A. 553 m/s B.43 m/s C.35 m/s D. 152 m/s
练1 [2021·株洲模拟](多选)将一小球以水平速度v0=10 m/s从O点向右抛出,经3 s小球恰好垂直落到斜面上的A点,不计空气阻力,g取10 m/s2,B点是小球做自由落体运动在斜面上的落点,如图所示,以下判断正确的是( )
A.斜面的倾角是30°
B.小球的抛出点距斜面上B点的竖直高度是15 m
C.若将小球以水平速度v′0=5 m/s向右抛出,它一定落在AB的中点P的上方
D.若将小球以水平速度v′0=5 m/s向右抛出,它一定落在AB的中点P处
练2 (多选)如图所示,a、b两小球(均可视为质点)分别从直径在水平线上的半圆轨道右端和足够长的斜面轨道顶端以大小相等的初速度同时由同一高度水平抛出,且同时落到各自轨道上.已知半圆轨道的半径为103 m,斜面轨道的倾角θ=30°,取g=10 m/s2,不计空气阻力,则( )
A.两小球抛出时的速度大小为10 m/s
B.两小球抛出时的速度大小为15 m/s
C.两小球在空中的运动时间为3 s
D.两小球在空中的运动时间为1.5 s
题后反思
有约束条件的平抛运动解题策略
第2讲 平抛运动的规律及应用
基础落实
知识点一
1.重力
2.匀变速
3.(1)匀速 (2)自由落体
4.(1)v0t 12gt2 x2+y2 gt2v0
(2)v0 gt vx2+vy2 gtv0
知识点二
1.斜向上方 重力
2.匀变速 抛物线
3.(1)匀速 (2)匀变速
思考辨析
(1)√ (2)× (3)× (4)√
教材改编
解析:根据合运动与分运动的等时性和独立性特点可知,两球应同时落地,为减小实验误差,应改变装置的高度,多次做实验,选项B、C正确;平抛运动的实验与小球的质量无关,选项A错误;此实验只能说明A球在竖直方向做自由落体运动,选项D错误.
答案:BC
考点突破
1.解析:小球做平抛运动的水平位移l=v0t,则小球下落的时间为t=lv0,A项正确;小球在竖直方向的位移y=12gt2=gl22v02 ,B正确;落到C点时,水平分位移与竖直分位移大小相等,即v0t=vy2t,所以vy=2v0,落到C点的速度v=v02+vy2 =5v0,方向为tan θ=vyv0=2,不等于60°,C、D两项错误.
答案:AB
2.解析:由平抛运动规律有x=v0t,y=12gt2,得v0=xg2y;动能Ek=12mv02=mgx24y∝x2y,故E2E1=x2x12·y1y2=3hh2·h0.5h=18,故B正确.
答案:B
3.解析:由题意可知,落地后,小球A的位移的大小为sA=xA2+yA2 =l2+2l2=5l,小球B的位移的大小为sB=xB2+yB2 =2l2+l2=5l,显然小球A、B的位移大小相等,A正确;小球A的运动时间为tA= 2yAg=4lg,小球B的运动时间为tB= 2yBg=2lg,则tA∶tB=2∶1,B错误;小球A的初速度为vxA=xAtA=l4lg=gl4,小球B的初速度为vxB=xBtB=2l2lg=2gl,则vA∶vB=1∶22,C错误;落地瞬间,小球A竖直方向的速度为vyA=4gl,小球B竖直方向的速度为vyB=2gl,则落地瞬间小球A的速度为vA=vxA2+vyA2 = 174gl,小球B的速度为vB=vxB2+vyB2 =4gl,显然vA>vB,D正确.
答案:AD
4.解析:(1)包裹脱离无人机后做平抛运动,在竖直方向做自由落体运动,则h=12gt2
解得t=2hg
水平方向上做匀速直线运动,所以水平距离为
x=v0t=v02hg
(2)包裹落地时,竖直方向速度为
vy=gt=g2hg
落地时速度为v=v02+vy2=v02 +2gh
(3)包裹做平抛运动,分解位移
x=v0t′
y=12gt′2
两式消去时间得包裹的轨迹方程为y=g2v02 x2
答案:1v02hg 2v02+2gh (3)y=g2v02 x2
例1 解析:由h=12gt2得,质点从O点到P点的运动时间为t=2 s,B错误;由tan θ=vyv0=gtv0=gt2v0t=2hx,质点在水平方向的位移为x=v0t=40 m,故Q是OM的中点,QM=20 m,A错误;质点在P点的速度大小为v=v02+vy2 =202 m/s,C错误;tan θ=vyv0=1,故质点在P点的速度方向与水平方向的夹角为45°,D正确.
答案:D
例2 解析:弹丸越过B点后做平抛运动,在竖直方向上有H=12gt2,水平方向上有x=vt,联立解得N、C之间的距离x=10 m,选项A错误;把弹丸从A点到B点的斜抛运动看成逆向的从B点到A点的平抛运动(逆向思维法),在竖直方向上有H-h=12gt′2,解得弹丸从A点运动B点的时间t′=0.8 s,则A点到竖直杆的水平距离x′=vt′=8 m,选项B正确;弹丸从B点运动到C点,由机械能守恒定律有mgH+12mv2=12mvC2,解得弹丸落地时的速度大小为vC=102 m/s,选项C正确;整个运动过程中,由功能关系得W=12mvC2-mgh,解得弹弓对弹丸做的功为W=4.1 J,选项D错误.
答案:BC
例3 解析:由题意,可知要使运动员不触及障碍物,则运动员下落到与障碍物等高时,根据几何关系可知运动员在水平方向发生的位移应该满足:x≥Htan53°+L
此时运动员在竖直方向下落的高度为H-h,设运动员运动的时间为t,则有:
H-h=12gt2
代入数据可得时间为:t=0.6 s
所以运动员从A点沿水平方向滑出的最小速度为:
vmin=6 m/s,故D正确,A、B、C错误.
答案:D
练1 解析:本题实质为平抛运动的临界问题.设排球离开手时的高度为H,网高为h,每边球场的长和宽均为L,排球刚好过网时,由平抛运动规律可知,在竖直方向H-h=12gt12 ,在水平方向L=v1t1,解得v1=18 m/s.排球刚好落到对方的场地的底线时,由平抛运动公式有,在竖直方向H=12gt22,在水平方向2L=v2t2,解得v2≈21.5 m/s,所以要使球落在对方场地,发球速度范围为18 m/s≤v≤21.5 m/s,故C符合要求.
答案:C
练2 解析:取水面上质量为m的水滴,从小孔P射出时由机械能守恒定律有mgy=12mv2,解得v=2gy,选项A错误;水从小孔P射出时做平抛运动,则x=vt,h-y=12gt2,解得x=2yh-y,可见x与小孔P的位置有关,因y+(h-y)=h为定值,由数学关系可知,当y=h-y,即y=12h时x最大,最大值为h,并不是y越小,x越大,选项D正确,B、C均错误.
答案:D
思维拓展
典例1 解析:设击球点高出桌面H,乒乓球在网的左、右两侧运动时间分别为t1、t2,乒乓球做平抛运动,经时间t在水平方向上的位移x=vt,在竖直方向上的位移y=12gt2,即t∝x,y∝t2,则t1t2=L2L,H-hH=t1t1+t22,整理得t1∶t2=1∶2,H∶h=9∶8,选项A、B错误;由加速度的定义式得g=Δv1t1,g=Δv2t2,则乒乓球在网的左、右两侧速度变化量之比Δv1∶Δv2=t1∶t2=1∶2,选项D正确;根据机械能守恒定律得12mv12 =mgH-h+12mv2,12mv22=mgH+12mv2,则乒乓球过网时与落到右侧桌边缘时的速率之比v1v2=v2+2gH-hv2+2gH=v2+2g·H9v2+2gH≠ 2g·H92gH=13,选项C错误.
答案:D
典例2 解析:小球在空中做平抛运动,在竖直方向上有y=12gt2,水平方向上有x=v0t,由几何关系有yx=tan θ,解得x=2v02 gtan θ,由图(b)可知2v02 g=0.10.5,解得小球在斜面顶端水平抛出时的初速度大小v0=1 m/s,选项A、B错误;由图(c)可知,图象末端的斜率增大,说明2v02 g增大,又重力加速度不变,可知做平抛运动的初速度增大,其原因可能为小球在弧形轨道上的释放位置变高或小球释放时有初速度,选项C错误;当θ=60°时,水平位移大小x=2×1210tan 60° m=35 m,由于小球恰好落在斜面底端,则斜面长度L=xcosθ=235 m,选项D正确.
答案:D
典例3 解析:忽略空气阻力,网球做的运动可视为平抛运动,在竖直方向上有h=12gtA2,2h=12gtB2,解得tA∶tB=1∶2,在水平方向上有x=vOAtA,x=vOBtB,则vOA∶vOB=2∶1,A、B均错误;动量为矢量,由图可知,二者与墙碰撞时其速度方向不相同,故二者碰到墙面时的动量不可能相同,C错误;由排除法知选项D正确(从抛出到与墙碰撞的过程中,根据机械能守恒定律有EkA=mgh+12mvOA2,EkB=mg·2h+12mvOB2,可得EkB-EkA=mgh+12mvOB2-12mvOA2=m2(2gh-vOB2),由数学知识可知,当vOB=2gh时,有EkA=EkB,D正确.
答案:D
典例4 解析:将小球到达B点时的速度沿水平方向和竖直方向分解,则vy=gt,R+R cos 60°=v0t,由几何关系得v0vy=tan 60°,解得v0=35 m/s,选项C正确.
答案:C
练1 解析:设斜面倾角为θ,对小球在A点的速度进行分解有tan θ=v0gt,解得θ=30°,A项正确;小球距过A点水平面的距离为h=12gt2=15 m,所以小球的抛出点距斜面上B点的竖直高度肯定大于15 m,B项错误;若小球的初速度为v′0=5 m/s,过A点作水平面,小球落到水平面的水平位移是小球以初速度v0=10 m/s抛出时的一半,延长小球运动的轨迹线,得到小球应该落在P、A之间,C项正确,D项错误.
答案:AC
练2 解析:两小球做平抛运动具有对称性,把左侧半圆对称到右侧,小球的落点为斜面与右侧半圆的交点,如图所示.由几何关系可知,小球落到斜面上时,在水平方向上有x=v0t,竖直方向上有y=12gt2,由几何关系得y=r sin 2θ,yx=tan θ,解得两小球抛出时的速度大小为v0=15 m/s,两小球在空中的运动时间为t=3 s,选项B、C均正确,A、D均错误.
答案:BC
同课章节目录
