2020-2021学年 高一物理 应用牛顿运动定律解决“三类”问题 期末复习强化学案Word版含答案
文档属性
| 名称 | 2020-2021学年 高一物理 应用牛顿运动定律解决“三类”问题 期末复习强化学案Word版含答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 604.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-14 13:18:10 | ||
图片预览



文档简介
应用牛顿运动定律解决“三类”问题
考点一 动力学中的图象问题
师生共研
1.常见的动力学图象
v?t图象、a?t图象、F?t图象、F?x(a?x)图象、F?a图象等.
2.解决问题策略
(1)动力学图象问题实质是求解力与运动的关系,解题关键在于弄清图象斜率、截距、交点、拐点、面积的物理意义.
(2)应用物理规律列出与图象对应的函数关系式,进而明确“图象与公式”“图象与物体”间的关系,以便对有关物理问题进行准确判断.
题型1|动力学中的v?t图象
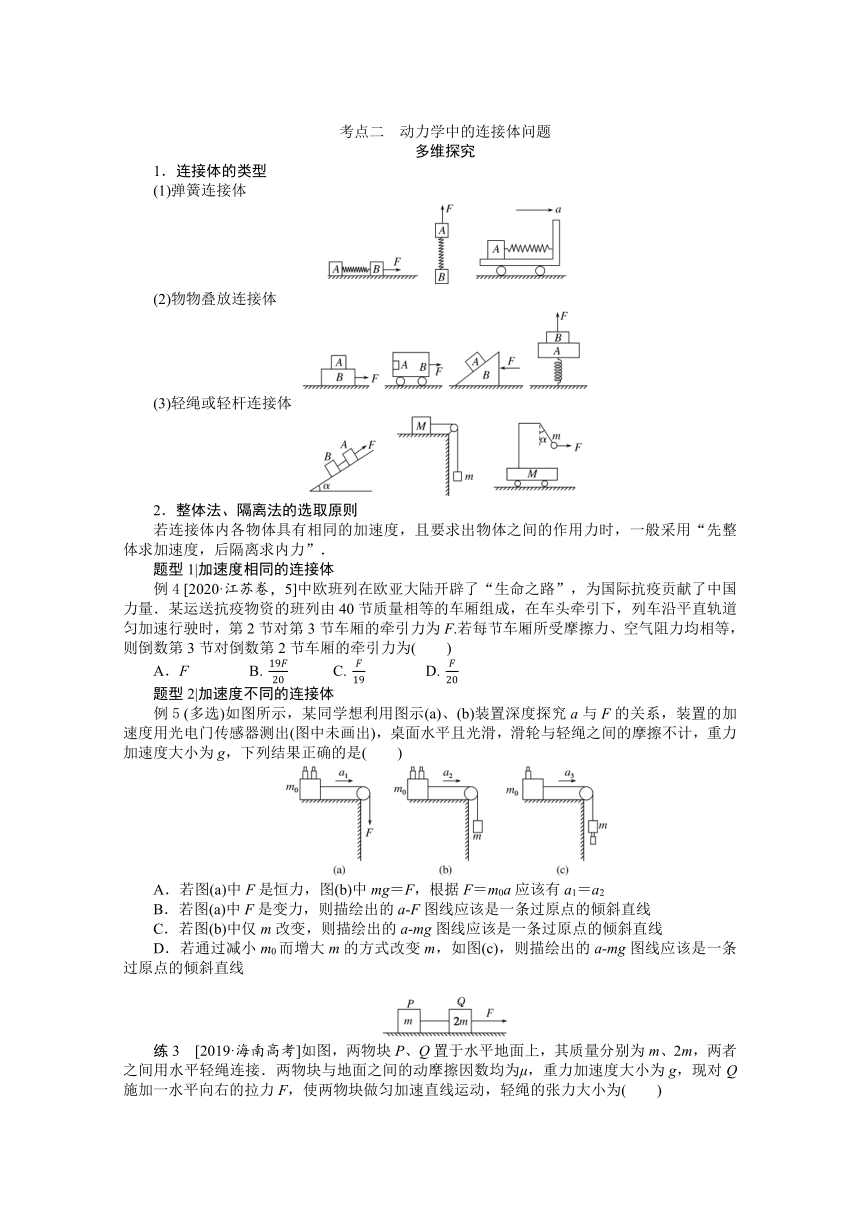
例1 [2019·全国卷Ⅲ,20](多选)如图(a),物块和木板叠放在实验台上,物块用一不可伸长的细绳与固定在实验台上的力传感器相连,细绳水平.t=0时,木板开始受到水平外力F的作用,在t=4 s时撤去外力.细绳对物块的拉力f随时间t变化的关系如图(b)所示,木板的速度v与时间t的关系如图(c)所示.木板与实验台之间的摩擦可以忽略.重力加速度取10 m/s2.由题给数据可以得出( )
A.木板的质量为1 kg
B.2 s~4 s内,力F的大小为0.4 N
C.0~2 s内,力F的大小保持不变
D.物块与木板之间的动摩擦因数为0.2
题型2|动力学中的F?t图象
例2 [2020·浙江7月,19]如图1所示,有一质量m=200 kg的物件在电机的牵引下从地面竖直向上经加速、匀速、匀减速至指定位置.当加速运动到总位移的14时开始计时,测得电机的牵引力随时间变化的F ? t图线如图2所示,t=34 s末速度减为0时恰好到达指定位置.若不计绳索的质量和空气阻力,求物件
图1 图2
(1)做匀减速运动的加速度大小和方向;
(2)匀速运动的速度大小;
(3)总位移的大小.
题型3|动力学中的F?x图象
例3 [2018·全国卷Ⅰ,15]如图,轻弹簧的下端固定在水平桌面上,上端放有物块P,系统处于静止状态.现用一竖直向上的力F作用在P上,使其向上做匀加速直线运动.以x表示P离开静止位置的位移,在弹簧恢复原长前,下列表示F和x之间关系的图象可能正确的是( )
练1 [2021·河南洛阳模拟]如图甲所示,一个质量为3 kg的物体放在粗糙水平地面上,从零时刻起,物体在水平力F作用下由静止开始做直线运动.在0~3 s时间内物体的加速度a随时间t的变化规律如图乙所示.则( )
A.F的最大值为12 N
B.0~1 s和2~3 s内物体加速度的方向相反
C.3 s末物体的速度最大,最大速度为8 m/s
D.在0~1 s内物体做匀加速运动,2~3 s内物体做匀减速运动
练2 [2021·山东德州市质检](多选)如图甲所示,直角三角形斜劈abc固定在水平面上.t=0时,一物块(可视为质点)从底端a以初速度v1沿斜面ab向上运动,到达顶点b时速率恰好为零,之后沿斜面bc下滑至底端c.若物块与斜面ab、bc间的动摩擦因数相等,物块在两斜面上运动的速率v随时间变化的规律如图乙所示,已知v1、v2、t1、t2、g,则下列物理量可求的是( )
A.斜面ab的倾角θ
B.物块与斜面间的动摩擦因数μ
C.物块的质量m
D.斜面bc的长度L
题后反思
解决图象综合问题的关键
(1)分清图象的类别:即分清横、纵坐标轴所代表的物理量,明确其物理意义,掌握物理图象所反映的物理过程,会分析临界点.
(2)明确能从图象中获得哪些信息:把图象与具体的题意、情境结合起来,再结合斜率、特殊点、面积等的物理意义,确定从图象中反馈出来的有用信息,这些信息往往是解题的突破口或关键点.
考点二 动力学中的连接体问题
多维探究
1.连接体的类型
(1)弹簧连接体
(2)物物叠放连接体
(3)轻绳或轻杆连接体
2.整体法、隔离法的选取原则
若连接体内各物体具有相同的加速度,且要求出物体之间的作用力时,一般采用“先整体求加速度,后隔离求内力”.
题型1|加速度相同的连接体
例4 [2020·江苏卷,5]中欧班列在欧亚大陆开辟了“生命之路”,为国际抗疫贡献了中国力量.某运送抗疫物资的班列由40节质量相等的车厢组成,在车头牵引下,列车沿平直轨道匀加速行驶时,第2节对第3节车厢的牵引力为F.若每节车厢所受摩擦力、空气阻力均相等,则倒数第3节对倒数第2节车厢的牵引力为( )
A.F B. 19F20 C. F19 D. F20
题型2|加速度不同的连接体
例5 (多选)如图所示,某同学想利用图示(a)、(b)装置深度探究a与F的关系,装置的加速度用光电门传感器测出(图中未画出),桌面水平且光滑,滑轮与轻绳之间的摩擦不计,重力加速度大小为g,下列结果正确的是( )
A.若图(a)中F是恒力,图(b)中mg=F,根据F=m0a应该有a1=a2
B.若图(a)中F是变力,则描绘出的a?F图线应该是一条过原点的倾斜直线
C.若图(b)中仅m改变,则描绘出的a?mg图线应该是一条过原点的倾斜直线
D.若通过减小m0而增大m的方式改变m,如图(c),则描绘出的a?mg图线应该是一条过原点的倾斜直线
练3 [2019·海南高考]如图,两物块P、Q置于水平地面上,其质量分别为m、2m,两者之间用水平轻绳连接.两物块与地面之间的动摩擦因数均为μ,重力加速度大小为g,现对Q施加一水平向右的拉力F,使两物块做匀加速直线运动,轻绳的张力大小为( )
A.F-2μmg B. 13F+μmg C. 13F-μmg D. 13F
练4 [2020·陕西宝鸡中学一模]如图甲所示,A、B两物体叠放在光滑水平面上,对物体A施加一水平力F,F?t图象如图乙所示,两物体在力F作用下由静止开始运动,且始终相对静止,规定水平向右为正方向,则下列说法正确的是( )
A.两物体在4 s时改变运动方向
B.在1~3 s时间内两物体间的摩擦力为零
C.6 s时两物体的速度为零
D.B物体所受的摩擦力方向始终与力F的方向相同
练5 (多选)如图所示,粗糙的水平地面上放着一个质量为M、倾角为θ的斜面体,斜面部分光滑,底面与水平地面间的动摩擦因数为μ,轻质弹簧一端与固定在斜面上的轻质挡板相连,另一端连接一质量为m的小球,弹簧的劲度系数为k.斜面体在水平向右的恒力F作用下,和小球一起以加速度a向右做匀加速直线运动(运动过程小球没离开斜面).重力加速度为g,以下说法正确的是( )
A.水平恒力大小为(M+m)a
B.地面对斜面体的摩擦力为μ(M+m)g
C.弹簧的形变量为macos θ+mgsin θk
D.斜面对小球的支持力为mgcos θ+masin θ
题后反思
解决连接体问题的关键
求解连接体内部物体之间的作用力时,一般选受力较少的隔离体为研究对象;求解具有相同的加速度的连接体所受的外部作用力或加速度时,一般选取系统整体为研究对象.大多数连接体问题中需要整体法和隔离法交替使用.
考点三 动力学中的临界和极值问题
多维探究
题型1|动力学中的临界问题
例6 如图所示,物体A叠放在物体B上,B置于光滑水平面上,A、B质量分别为mA=6 kg、mB=2 kg,A、B之间的动摩擦因数μ=0.2,开始时F=10 N,此后逐渐增加,在增大到45 N的过程中,则( )
A.当拉力F<12 N时,物体均保持静止状态
B.两物体开始没有相对运动,当拉力超过12 N时,开始相对滑动
C.两物体从受力开始就有相对运动
D.两物体始终没有相对运动
题型2|动力学中的极值问题
例7 [2020·成都二模]一弹簧一端固定在倾角为37°的光滑斜面的底端,另一端拴住质量m1=4 kg的物块P.Q为一重物,已知Q的质量m2=8 kg,弹簧的质量不计,劲度系数k=600 N/m,系统处于静止,如图所示.现给Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后,F为恒力(sin 37°=0.6,g取10 m/s2).求:
(1)P、Q一起做匀加速运动的加速度大小;
(2)F的最大值与最小值.
练6 (多选)如图所示,在水平光滑桌面上放有m1和m2两个小物块,它们中间有细线连接.已知m1=3 kg,m2=2 kg,连接它们的细线最大能承受6 N的拉力.现用水平外力F1向左拉m1或用水平外力F2向右拉m2,为保持细线不断,则( )
A.F1的最大值为10 N B.F1的最大值为15 N
C.F2的最大值为10 N D.F2的最大值为15 N
练7 如图所示,在光滑水平面上有一辆小车A,其质量为mA=2.0 kg,小车上放一个物体B,其质量为mB=1.0 kg.如图甲所示,给B一个水平推力F,当F增大到稍大于3.0 N时,A、B开始相对滑动.如果撤去F,对A施加一水平推力F′,如图乙所示.要使A、B不相对滑动,则F′的最大值Fm′为( )
A.3.0 N B.4.0 N C.5.0 N D.6.0 N
思维拓展
数形结合解决动力学问题
如图甲所示,一物块放在粗糙的水平面上,从t=0时刻开始,以一定的初速度向左运动,同时在物块上加一斜向右上的恒力F的作用,F与水平方向的夹角θ=37°,物块的质量为2 kg,物块与地面间的动摩擦因数μ=0.5,物块向左运动的v ? t图象如图乙所示,(已知cos 37°=0.8,sin 37°=0.6,g取10 m/s2),求:
(1)拉力F的大小.
(2)物块再回到t=0时刻的位置时的速度v1的大小.
(3)若在t=0.5 s时拉力的方向不变,大小改变,要使物块再回到t=0时刻的位置时速度大小和t=0时刻的速度大小相等,则拉力F′应变为多少?(结果保留两位小数)
[教你解决问题]
第一步:读题抓关键点―→获取信息
第二步:读图析图―→获取信息
练 如图甲所示,光滑斜面倾角为θ,用一水平外力F推着物体,逐渐增大F,物体沿斜面做变加速运动,其加速度a随外力F变化的图象如图乙所示,重力加速度g取10 m/s2.
(1)求物体的质量m;
(2)若斜面足够长,且撤去推力时物体的速度是沿斜面向上的12 m/s,求撤去推力后第3 s内物体的位移;
(3)要使物体在斜面上保持静止,所施加的最小推力是多大?方向如何?
专题二 应用牛顿运动定律解决“三类”问题
考点突破
例1 解析:本题考查牛顿运动定律的综合应用,体现了物理学科科学推理的核心素养.
分析知木板受到的摩擦力f′=f. 0~2 s,木板静止,F=f′,F逐渐增大,所以C错误;4 s~5 s,木板加速度大小a2=0.4-0.21 m/s2=0.2 m/s2,对木板受力分析,f′=ma2=0.2 N,得m=1 kg,所以A正确;2 s~4 s,对木板有F-f′=ma1,F=f′+ma1=0.2 N+1×0.4-02N=0.4 N,所以B正确;由于无法确定物块的质量,则尽管知道滑动摩擦力大小,仍无法确定物块与木板间的动摩擦因数,故D错误.
答案:AB
例2 解析:(1)牛顿第二定律mg-FT=ma
得a=g-FTm=0.125 m/s2
竖直向下
(2)运动学公式v=at2=1 m/s
(3)匀速上升的位移h1=vt1=26 m
匀减速上升的位移h2=v2t2=4 m
h-h1-h2h=14
总位移h=40 m
答案:(1)0.125 m/s2,方向竖直向下 (2)1 m/s (3)40 m
例3
解析:设物块P静止时,弹簧的长度为x0,物块P受重力mg、弹簧弹力k(l-x0-x)及力F,根据牛顿第二定律,得F+k(l-x0-x)-mg=ma
且k(l-x0)=mg
故F=kx+ma.
根据数学知识知F-x图象是截距为ma的一次函数图象.故选项A正确.
答案:A
练1 解析:由图象可知,物体在1~2 s内做匀加速直线运动,a=4 m/s2,由牛顿第二定律得F-μmg=ma,故F=ma+μmg>12 N,故A错误;由a?t图象的特点知加速度一直为正,故B错误;a?t图象与时间轴围成图形的面积为Δv,而初速度为零,故3 s末速度最大为8 m/s,故C正确;整个过程中,物体一直做加速运动,故D错误.
答案:C
练2 解析:设物块上滑与下滑的加速度大小分别为a1和a2.由v?t图象的斜率等于加速度,得a1=v1t1,a2=v2t2-t1;物块上滑根据牛顿第二定律有mgsin θ+μmgcos θ=ma1,物块下滑根据牛顿第二定律有:mgsin(90°-θ)-μmgcos(90°-θ)=ma2,联立以上四式,由数学知识可求得斜面的ab倾角θ、物块与斜面间的动摩擦因数μ.不能求出物块的质量m,故选项A、B正确,C错误;斜面bc的长度为L=v2t2-t12,则可以求出L,选项D正确.
答案:ABD
例4 解析:设列车做匀加速直线运动的加速度为a,可将后面的38节车厢作为一个整体进行分析,设每节车厢的质量均为m,每节车厢所受的摩擦力和空气阻力的合力大小均为f,则有F-38f=38ma,再将最后面的2节车厢作为一个整体进行分析,设倒数第3节车厢对倒数第2节车厢的牵引力为F′,则有F′-2f=2ma,联立解得F′=119F,C项正确,A、B、D项均错误.
答案:C
例5 解析:题干关键词:“桌面水平且光滑”,“滑轮与轻绳之间的摩擦不计”
A选项:图(a)装置,以物块和砝码为研究对象,有F=m0a1,得a1=Fm0
图(b)装置,以物块和砝码为研究对象,有T=m0a2
以装置下端质量为m的物体为研究对象,有
mg-T=ma2
所以a2=mgm0+m
a1≠a2,所以A选项错误.
B选项:根据a1=Fm0,m0是定值,知描绘出的a?F图线是一条过原点的倾斜直线,所以B选项正确.
C选项:根据a2=mgm0+m,知随着m增加,1m0+m在减小,并非定值,所以描绘出的a?mg图线不是一条过原点的倾斜直线,所以C选项错误.
D选项:根据a2=mgm0+m,分析选项操作表述,随着m增加, 1m0+m是定值,所以描绘出的a?mg图线是一条过原点的倾斜直线,所以D选项正确.
答案:BD
练3 解析:本题为连接体问题,通过对本题的分析解答,考查了学生的推理能力,同时也渗透了科学思维中的模型建构及科学推理要素.
对整体进行受力分析:F-μ·3mg=3ma,
对P进行受力分析:T-μmg=ma,
联立解得轻绳的张力大小为T=F3,故A、B、C错误,D正确.
答案:D
练4 解析:以A、B为整体,由牛顿第二定律知,加速度a=FmA+mB,方向一直向右,整体一直做加速运动,选项A、C错误;对B分析,摩擦力Ff=m0a,方向始终与力F的方向相同,1~6 s内摩擦力不为0,选项B错误,D正确.
答案:D
练5 解析:以小球和斜面体组成的系统为研究对象,并进行受力分析,结合题意可知地面对斜面体的摩擦力为f=μ(M+m)g,对系统应用牛顿第二定律有F-μ(M+m)g=(M+m)a,解得F=(M+m)a+μ(M+m)g,选项A错误,B正确;沿斜面方向和垂直斜面方向上分解小球的加速度,应用牛顿第二定律有kx-mgsin θ=macos θ,mgcos θ-N=masin θ,解得弹簧的形变量为x=macos θ+mgsin θk,斜面对小球的支持力N=mgcos θ-masin θ,选项C正确,D错误.
答案:BC
例6 解析:解法一:(临界法)A、B间静摩擦力达到最大值,是A、B发生相对运动的临界状态.此时,以A为研究对象,根据牛顿第二定律F-Ff=mAaA,再以B为研究对象,根据牛顿第二定律Ff=mBaB,当Ff为最大静摩擦力时,解得a=6 m/s2,F=48 N,由此可以看出当F<48 N时,A、B间的摩擦力达不到最大静摩擦力,也就是说,A、B间不会发生相对运动,选项D正确.
解法二:(假设法)假设F=12 N,以A为研究对象,根据牛顿第二定律F-Ff=mAaA,再以B为研究对象,根据牛顿第二定律Ff=mBaB,解得Ff=3 N答案:D
例7 解析:(1)设刚开始时弹簧的压缩量为x0,在沿斜面方向上有(m1+m2)gsin θ=kx0,因为在前0.2 s时间内,F为变力,0.2 s以后,F为恒力,所以在0.2 s时,P对Q的作用力为零,设0.2 s时,弹簧的压缩量为x1,对P由牛顿第二定律知,沿斜面方向上有kx1-m1gsin θ=m1a,前0.2 s时间内P、Q向上运动的距离为x0-x1=12at2,联立解得a=3 m/s2.
(2)当P、Q开始运动时拉力最小,此时对P、Q整体有Fmin+kx0-(m1+m2)gsin θ=(m1+m2)a,解得Fmin=36 N,当P、Q分离时拉力最大,此时对Q有Fmax=m2(a+gsin θ)=72 N.
答案:(1)3 m/s2 (2)72 N 36 N
练6 解析:若向左拉m1,对m2分析,则FTm=m2a,得出最大加速度a=3 m/s2;对两物块系统:F1=(m1+m2)a=(2+3)×3 N=15 N,选项B正确,A错误;若向右拉m2,对m1分析,则FTm=m1a′,得出最大加速度a′=2 m/s2;对两物块系统:F2=(m1+m2)a′=(2+3)×2 N=10 N,选项D错误,C正确.
答案:BC
练7 解析:根据图甲所示,设A、B间的静摩擦力达到最大值Ffm时,系统的加速度为a.根据牛顿第二定律,对A、B整体有F=(mA+mB)a,对A有Ffm=mAa,代入数据解得Ffm=2.0 N.
根据图乙所示情况,设A、B刚开始滑动时系统的加速度为a′,根据牛顿第二定律有:
Ffm=mBa′,Fm′=(mA+mB)a′,
代入数据解得Fm′=6.0 N.故选项D正确.
答案:D
思维拓展
典例 解析:(1)物块向左运动时,
由图象知,初速度v0=6 m/s,
加速度大小a1=ΔvΔt=12 m/s2.
由牛顿第二定律Fcos θ+μ(mg-Fsin θ)=ma1
解得F=28 N.
(2)物块在拉力作用下从速度为零开始向右运动时,由图象可知,回到t=0时刻的位置的位移x=12×6×0.5 m=1.5 m.
由牛顿第二定律Fcos θ-μ(mg-Fsin θ)=ma2
求得a2=10.4 m/s2.
由运动学公式v12=2a2x.
得物块回到t=0时刻位置的速度
v1=25195 m/s.
(3)要使物块回到t=0时刻位置的速度大小和t=0时刻的速度大小相等,因此物块做的是类上抛运动,向右运动时的加速度大小
a3=a1=12 m/s2.
由牛顿第二定律F′cos θ-μ(mg-F′sin θ)=ma3
求得F′=30.91 N.
答案:(1)28 N (2) 25195 m/s (3)30.91 N
练 解析:(1)当外力为零时,加速度为6 m/s2,
根据牛顿第二定律得mgsin θ=ma
解得sin θ=0.6
当外力为20 N时,加速度为2 m/s2,根据牛顿第二定律得Fcos θ-mgsin θ=ma′
解得m=2 kg
(2)根据匀变速直线运动规律可得x=vt3-12at32-vt2-12at22=-3 m
所以位移大小为3 m,方向沿斜面向下
(3)要使物体能静止在斜面上,根据平衡条件知,当推力垂直于支持力,即沿斜面向上时,推力最小,为F=mgsin θ=12 N
答案:
(1)2 kg (2)3 m,方向沿斜面向下
(3)12 N,沿斜面向上
考点一 动力学中的图象问题
师生共研
1.常见的动力学图象
v?t图象、a?t图象、F?t图象、F?x(a?x)图象、F?a图象等.
2.解决问题策略
(1)动力学图象问题实质是求解力与运动的关系,解题关键在于弄清图象斜率、截距、交点、拐点、面积的物理意义.
(2)应用物理规律列出与图象对应的函数关系式,进而明确“图象与公式”“图象与物体”间的关系,以便对有关物理问题进行准确判断.
题型1|动力学中的v?t图象
例1 [2019·全国卷Ⅲ,20](多选)如图(a),物块和木板叠放在实验台上,物块用一不可伸长的细绳与固定在实验台上的力传感器相连,细绳水平.t=0时,木板开始受到水平外力F的作用,在t=4 s时撤去外力.细绳对物块的拉力f随时间t变化的关系如图(b)所示,木板的速度v与时间t的关系如图(c)所示.木板与实验台之间的摩擦可以忽略.重力加速度取10 m/s2.由题给数据可以得出( )
A.木板的质量为1 kg
B.2 s~4 s内,力F的大小为0.4 N
C.0~2 s内,力F的大小保持不变
D.物块与木板之间的动摩擦因数为0.2
题型2|动力学中的F?t图象
例2 [2020·浙江7月,19]如图1所示,有一质量m=200 kg的物件在电机的牵引下从地面竖直向上经加速、匀速、匀减速至指定位置.当加速运动到总位移的14时开始计时,测得电机的牵引力随时间变化的F ? t图线如图2所示,t=34 s末速度减为0时恰好到达指定位置.若不计绳索的质量和空气阻力,求物件
图1 图2
(1)做匀减速运动的加速度大小和方向;
(2)匀速运动的速度大小;
(3)总位移的大小.
题型3|动力学中的F?x图象
例3 [2018·全国卷Ⅰ,15]如图,轻弹簧的下端固定在水平桌面上,上端放有物块P,系统处于静止状态.现用一竖直向上的力F作用在P上,使其向上做匀加速直线运动.以x表示P离开静止位置的位移,在弹簧恢复原长前,下列表示F和x之间关系的图象可能正确的是( )
练1 [2021·河南洛阳模拟]如图甲所示,一个质量为3 kg的物体放在粗糙水平地面上,从零时刻起,物体在水平力F作用下由静止开始做直线运动.在0~3 s时间内物体的加速度a随时间t的变化规律如图乙所示.则( )
A.F的最大值为12 N
B.0~1 s和2~3 s内物体加速度的方向相反
C.3 s末物体的速度最大,最大速度为8 m/s
D.在0~1 s内物体做匀加速运动,2~3 s内物体做匀减速运动
练2 [2021·山东德州市质检](多选)如图甲所示,直角三角形斜劈abc固定在水平面上.t=0时,一物块(可视为质点)从底端a以初速度v1沿斜面ab向上运动,到达顶点b时速率恰好为零,之后沿斜面bc下滑至底端c.若物块与斜面ab、bc间的动摩擦因数相等,物块在两斜面上运动的速率v随时间变化的规律如图乙所示,已知v1、v2、t1、t2、g,则下列物理量可求的是( )
A.斜面ab的倾角θ
B.物块与斜面间的动摩擦因数μ
C.物块的质量m
D.斜面bc的长度L
题后反思
解决图象综合问题的关键
(1)分清图象的类别:即分清横、纵坐标轴所代表的物理量,明确其物理意义,掌握物理图象所反映的物理过程,会分析临界点.
(2)明确能从图象中获得哪些信息:把图象与具体的题意、情境结合起来,再结合斜率、特殊点、面积等的物理意义,确定从图象中反馈出来的有用信息,这些信息往往是解题的突破口或关键点.
考点二 动力学中的连接体问题
多维探究
1.连接体的类型
(1)弹簧连接体
(2)物物叠放连接体
(3)轻绳或轻杆连接体
2.整体法、隔离法的选取原则
若连接体内各物体具有相同的加速度,且要求出物体之间的作用力时,一般采用“先整体求加速度,后隔离求内力”.
题型1|加速度相同的连接体
例4 [2020·江苏卷,5]中欧班列在欧亚大陆开辟了“生命之路”,为国际抗疫贡献了中国力量.某运送抗疫物资的班列由40节质量相等的车厢组成,在车头牵引下,列车沿平直轨道匀加速行驶时,第2节对第3节车厢的牵引力为F.若每节车厢所受摩擦力、空气阻力均相等,则倒数第3节对倒数第2节车厢的牵引力为( )
A.F B. 19F20 C. F19 D. F20
题型2|加速度不同的连接体
例5 (多选)如图所示,某同学想利用图示(a)、(b)装置深度探究a与F的关系,装置的加速度用光电门传感器测出(图中未画出),桌面水平且光滑,滑轮与轻绳之间的摩擦不计,重力加速度大小为g,下列结果正确的是( )
A.若图(a)中F是恒力,图(b)中mg=F,根据F=m0a应该有a1=a2
B.若图(a)中F是变力,则描绘出的a?F图线应该是一条过原点的倾斜直线
C.若图(b)中仅m改变,则描绘出的a?mg图线应该是一条过原点的倾斜直线
D.若通过减小m0而增大m的方式改变m,如图(c),则描绘出的a?mg图线应该是一条过原点的倾斜直线
练3 [2019·海南高考]如图,两物块P、Q置于水平地面上,其质量分别为m、2m,两者之间用水平轻绳连接.两物块与地面之间的动摩擦因数均为μ,重力加速度大小为g,现对Q施加一水平向右的拉力F,使两物块做匀加速直线运动,轻绳的张力大小为( )
A.F-2μmg B. 13F+μmg C. 13F-μmg D. 13F
练4 [2020·陕西宝鸡中学一模]如图甲所示,A、B两物体叠放在光滑水平面上,对物体A施加一水平力F,F?t图象如图乙所示,两物体在力F作用下由静止开始运动,且始终相对静止,规定水平向右为正方向,则下列说法正确的是( )
A.两物体在4 s时改变运动方向
B.在1~3 s时间内两物体间的摩擦力为零
C.6 s时两物体的速度为零
D.B物体所受的摩擦力方向始终与力F的方向相同
练5 (多选)如图所示,粗糙的水平地面上放着一个质量为M、倾角为θ的斜面体,斜面部分光滑,底面与水平地面间的动摩擦因数为μ,轻质弹簧一端与固定在斜面上的轻质挡板相连,另一端连接一质量为m的小球,弹簧的劲度系数为k.斜面体在水平向右的恒力F作用下,和小球一起以加速度a向右做匀加速直线运动(运动过程小球没离开斜面).重力加速度为g,以下说法正确的是( )
A.水平恒力大小为(M+m)a
B.地面对斜面体的摩擦力为μ(M+m)g
C.弹簧的形变量为macos θ+mgsin θk
D.斜面对小球的支持力为mgcos θ+masin θ
题后反思
解决连接体问题的关键
求解连接体内部物体之间的作用力时,一般选受力较少的隔离体为研究对象;求解具有相同的加速度的连接体所受的外部作用力或加速度时,一般选取系统整体为研究对象.大多数连接体问题中需要整体法和隔离法交替使用.
考点三 动力学中的临界和极值问题
多维探究
题型1|动力学中的临界问题
例6 如图所示,物体A叠放在物体B上,B置于光滑水平面上,A、B质量分别为mA=6 kg、mB=2 kg,A、B之间的动摩擦因数μ=0.2,开始时F=10 N,此后逐渐增加,在增大到45 N的过程中,则( )
A.当拉力F<12 N时,物体均保持静止状态
B.两物体开始没有相对运动,当拉力超过12 N时,开始相对滑动
C.两物体从受力开始就有相对运动
D.两物体始终没有相对运动
题型2|动力学中的极值问题
例7 [2020·成都二模]一弹簧一端固定在倾角为37°的光滑斜面的底端,另一端拴住质量m1=4 kg的物块P.Q为一重物,已知Q的质量m2=8 kg,弹簧的质量不计,劲度系数k=600 N/m,系统处于静止,如图所示.现给Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速运动,已知在前0.2 s时间内,F为变力,0.2 s以后,F为恒力(sin 37°=0.6,g取10 m/s2).求:
(1)P、Q一起做匀加速运动的加速度大小;
(2)F的最大值与最小值.
练6 (多选)如图所示,在水平光滑桌面上放有m1和m2两个小物块,它们中间有细线连接.已知m1=3 kg,m2=2 kg,连接它们的细线最大能承受6 N的拉力.现用水平外力F1向左拉m1或用水平外力F2向右拉m2,为保持细线不断,则( )
A.F1的最大值为10 N B.F1的最大值为15 N
C.F2的最大值为10 N D.F2的最大值为15 N
练7 如图所示,在光滑水平面上有一辆小车A,其质量为mA=2.0 kg,小车上放一个物体B,其质量为mB=1.0 kg.如图甲所示,给B一个水平推力F,当F增大到稍大于3.0 N时,A、B开始相对滑动.如果撤去F,对A施加一水平推力F′,如图乙所示.要使A、B不相对滑动,则F′的最大值Fm′为( )
A.3.0 N B.4.0 N C.5.0 N D.6.0 N
思维拓展
数形结合解决动力学问题
如图甲所示,一物块放在粗糙的水平面上,从t=0时刻开始,以一定的初速度向左运动,同时在物块上加一斜向右上的恒力F的作用,F与水平方向的夹角θ=37°,物块的质量为2 kg,物块与地面间的动摩擦因数μ=0.5,物块向左运动的v ? t图象如图乙所示,(已知cos 37°=0.8,sin 37°=0.6,g取10 m/s2),求:
(1)拉力F的大小.
(2)物块再回到t=0时刻的位置时的速度v1的大小.
(3)若在t=0.5 s时拉力的方向不变,大小改变,要使物块再回到t=0时刻的位置时速度大小和t=0时刻的速度大小相等,则拉力F′应变为多少?(结果保留两位小数)
[教你解决问题]
第一步:读题抓关键点―→获取信息
第二步:读图析图―→获取信息
练 如图甲所示,光滑斜面倾角为θ,用一水平外力F推着物体,逐渐增大F,物体沿斜面做变加速运动,其加速度a随外力F变化的图象如图乙所示,重力加速度g取10 m/s2.
(1)求物体的质量m;
(2)若斜面足够长,且撤去推力时物体的速度是沿斜面向上的12 m/s,求撤去推力后第3 s内物体的位移;
(3)要使物体在斜面上保持静止,所施加的最小推力是多大?方向如何?
专题二 应用牛顿运动定律解决“三类”问题
考点突破
例1 解析:本题考查牛顿运动定律的综合应用,体现了物理学科科学推理的核心素养.
分析知木板受到的摩擦力f′=f. 0~2 s,木板静止,F=f′,F逐渐增大,所以C错误;4 s~5 s,木板加速度大小a2=0.4-0.21 m/s2=0.2 m/s2,对木板受力分析,f′=ma2=0.2 N,得m=1 kg,所以A正确;2 s~4 s,对木板有F-f′=ma1,F=f′+ma1=0.2 N+1×0.4-02N=0.4 N,所以B正确;由于无法确定物块的质量,则尽管知道滑动摩擦力大小,仍无法确定物块与木板间的动摩擦因数,故D错误.
答案:AB
例2 解析:(1)牛顿第二定律mg-FT=ma
得a=g-FTm=0.125 m/s2
竖直向下
(2)运动学公式v=at2=1 m/s
(3)匀速上升的位移h1=vt1=26 m
匀减速上升的位移h2=v2t2=4 m
h-h1-h2h=14
总位移h=40 m
答案:(1)0.125 m/s2,方向竖直向下 (2)1 m/s (3)40 m
例3
解析:设物块P静止时,弹簧的长度为x0,物块P受重力mg、弹簧弹力k(l-x0-x)及力F,根据牛顿第二定律,得F+k(l-x0-x)-mg=ma
且k(l-x0)=mg
故F=kx+ma.
根据数学知识知F-x图象是截距为ma的一次函数图象.故选项A正确.
答案:A
练1 解析:由图象可知,物体在1~2 s内做匀加速直线运动,a=4 m/s2,由牛顿第二定律得F-μmg=ma,故F=ma+μmg>12 N,故A错误;由a?t图象的特点知加速度一直为正,故B错误;a?t图象与时间轴围成图形的面积为Δv,而初速度为零,故3 s末速度最大为8 m/s,故C正确;整个过程中,物体一直做加速运动,故D错误.
答案:C
练2 解析:设物块上滑与下滑的加速度大小分别为a1和a2.由v?t图象的斜率等于加速度,得a1=v1t1,a2=v2t2-t1;物块上滑根据牛顿第二定律有mgsin θ+μmgcos θ=ma1,物块下滑根据牛顿第二定律有:mgsin(90°-θ)-μmgcos(90°-θ)=ma2,联立以上四式,由数学知识可求得斜面的ab倾角θ、物块与斜面间的动摩擦因数μ.不能求出物块的质量m,故选项A、B正确,C错误;斜面bc的长度为L=v2t2-t12,则可以求出L,选项D正确.
答案:ABD
例4 解析:设列车做匀加速直线运动的加速度为a,可将后面的38节车厢作为一个整体进行分析,设每节车厢的质量均为m,每节车厢所受的摩擦力和空气阻力的合力大小均为f,则有F-38f=38ma,再将最后面的2节车厢作为一个整体进行分析,设倒数第3节车厢对倒数第2节车厢的牵引力为F′,则有F′-2f=2ma,联立解得F′=119F,C项正确,A、B、D项均错误.
答案:C
例5 解析:题干关键词:“桌面水平且光滑”,“滑轮与轻绳之间的摩擦不计”
A选项:图(a)装置,以物块和砝码为研究对象,有F=m0a1,得a1=Fm0
图(b)装置,以物块和砝码为研究对象,有T=m0a2
以装置下端质量为m的物体为研究对象,有
mg-T=ma2
所以a2=mgm0+m
a1≠a2,所以A选项错误.
B选项:根据a1=Fm0,m0是定值,知描绘出的a?F图线是一条过原点的倾斜直线,所以B选项正确.
C选项:根据a2=mgm0+m,知随着m增加,1m0+m在减小,并非定值,所以描绘出的a?mg图线不是一条过原点的倾斜直线,所以C选项错误.
D选项:根据a2=mgm0+m,分析选项操作表述,随着m增加, 1m0+m是定值,所以描绘出的a?mg图线是一条过原点的倾斜直线,所以D选项正确.
答案:BD
练3 解析:本题为连接体问题,通过对本题的分析解答,考查了学生的推理能力,同时也渗透了科学思维中的模型建构及科学推理要素.
对整体进行受力分析:F-μ·3mg=3ma,
对P进行受力分析:T-μmg=ma,
联立解得轻绳的张力大小为T=F3,故A、B、C错误,D正确.
答案:D
练4 解析:以A、B为整体,由牛顿第二定律知,加速度a=FmA+mB,方向一直向右,整体一直做加速运动,选项A、C错误;对B分析,摩擦力Ff=m0a,方向始终与力F的方向相同,1~6 s内摩擦力不为0,选项B错误,D正确.
答案:D
练5 解析:以小球和斜面体组成的系统为研究对象,并进行受力分析,结合题意可知地面对斜面体的摩擦力为f=μ(M+m)g,对系统应用牛顿第二定律有F-μ(M+m)g=(M+m)a,解得F=(M+m)a+μ(M+m)g,选项A错误,B正确;沿斜面方向和垂直斜面方向上分解小球的加速度,应用牛顿第二定律有kx-mgsin θ=macos θ,mgcos θ-N=masin θ,解得弹簧的形变量为x=macos θ+mgsin θk,斜面对小球的支持力N=mgcos θ-masin θ,选项C正确,D错误.
答案:BC
例6 解析:解法一:(临界法)A、B间静摩擦力达到最大值,是A、B发生相对运动的临界状态.此时,以A为研究对象,根据牛顿第二定律F-Ff=mAaA,再以B为研究对象,根据牛顿第二定律Ff=mBaB,当Ff为最大静摩擦力时,解得a=6 m/s2,F=48 N,由此可以看出当F<48 N时,A、B间的摩擦力达不到最大静摩擦力,也就是说,A、B间不会发生相对运动,选项D正确.
解法二:(假设法)假设F=12 N,以A为研究对象,根据牛顿第二定律F-Ff=mAaA,再以B为研究对象,根据牛顿第二定律Ff=mBaB,解得Ff=3 N
例7 解析:(1)设刚开始时弹簧的压缩量为x0,在沿斜面方向上有(m1+m2)gsin θ=kx0,因为在前0.2 s时间内,F为变力,0.2 s以后,F为恒力,所以在0.2 s时,P对Q的作用力为零,设0.2 s时,弹簧的压缩量为x1,对P由牛顿第二定律知,沿斜面方向上有kx1-m1gsin θ=m1a,前0.2 s时间内P、Q向上运动的距离为x0-x1=12at2,联立解得a=3 m/s2.
(2)当P、Q开始运动时拉力最小,此时对P、Q整体有Fmin+kx0-(m1+m2)gsin θ=(m1+m2)a,解得Fmin=36 N,当P、Q分离时拉力最大,此时对Q有Fmax=m2(a+gsin θ)=72 N.
答案:(1)3 m/s2 (2)72 N 36 N
练6 解析:若向左拉m1,对m2分析,则FTm=m2a,得出最大加速度a=3 m/s2;对两物块系统:F1=(m1+m2)a=(2+3)×3 N=15 N,选项B正确,A错误;若向右拉m2,对m1分析,则FTm=m1a′,得出最大加速度a′=2 m/s2;对两物块系统:F2=(m1+m2)a′=(2+3)×2 N=10 N,选项D错误,C正确.
答案:BC
练7 解析:根据图甲所示,设A、B间的静摩擦力达到最大值Ffm时,系统的加速度为a.根据牛顿第二定律,对A、B整体有F=(mA+mB)a,对A有Ffm=mAa,代入数据解得Ffm=2.0 N.
根据图乙所示情况,设A、B刚开始滑动时系统的加速度为a′,根据牛顿第二定律有:
Ffm=mBa′,Fm′=(mA+mB)a′,
代入数据解得Fm′=6.0 N.故选项D正确.
答案:D
思维拓展
典例 解析:(1)物块向左运动时,
由图象知,初速度v0=6 m/s,
加速度大小a1=ΔvΔt=12 m/s2.
由牛顿第二定律Fcos θ+μ(mg-Fsin θ)=ma1
解得F=28 N.
(2)物块在拉力作用下从速度为零开始向右运动时,由图象可知,回到t=0时刻的位置的位移x=12×6×0.5 m=1.5 m.
由牛顿第二定律Fcos θ-μ(mg-Fsin θ)=ma2
求得a2=10.4 m/s2.
由运动学公式v12=2a2x.
得物块回到t=0时刻位置的速度
v1=25195 m/s.
(3)要使物块回到t=0时刻位置的速度大小和t=0时刻的速度大小相等,因此物块做的是类上抛运动,向右运动时的加速度大小
a3=a1=12 m/s2.
由牛顿第二定律F′cos θ-μ(mg-F′sin θ)=ma3
求得F′=30.91 N.
答案:(1)28 N (2) 25195 m/s (3)30.91 N
练 解析:(1)当外力为零时,加速度为6 m/s2,
根据牛顿第二定律得mgsin θ=ma
解得sin θ=0.6
当外力为20 N时,加速度为2 m/s2,根据牛顿第二定律得Fcos θ-mgsin θ=ma′
解得m=2 kg
(2)根据匀变速直线运动规律可得x=vt3-12at32-vt2-12at22=-3 m
所以位移大小为3 m,方向沿斜面向下
(3)要使物体能静止在斜面上,根据平衡条件知,当推力垂直于支持力,即沿斜面向上时,推力最小,为F=mgsin θ=12 N
答案:
(1)2 kg (2)3 m,方向沿斜面向下
(3)12 N,沿斜面向上
同课章节目录
