2020-2021学年 高一物理 力的合成与分解 强化学案Word版含答案
文档属性
| 名称 | 2020-2021学年 高一物理 力的合成与分解 强化学案Word版含答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 928.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-14 13:28:04 | ||
图片预览




文档简介
力的合成与分解
知识点一 力的合成
1.合力与分力
(1)定义:如果几个力共同作用产生的效果与一个力的作用效果相同,这一个力就叫做那几个力的________,那几个力叫做这一个力的________.
(2)关系:合力与分力是________________关系.
2.共点力
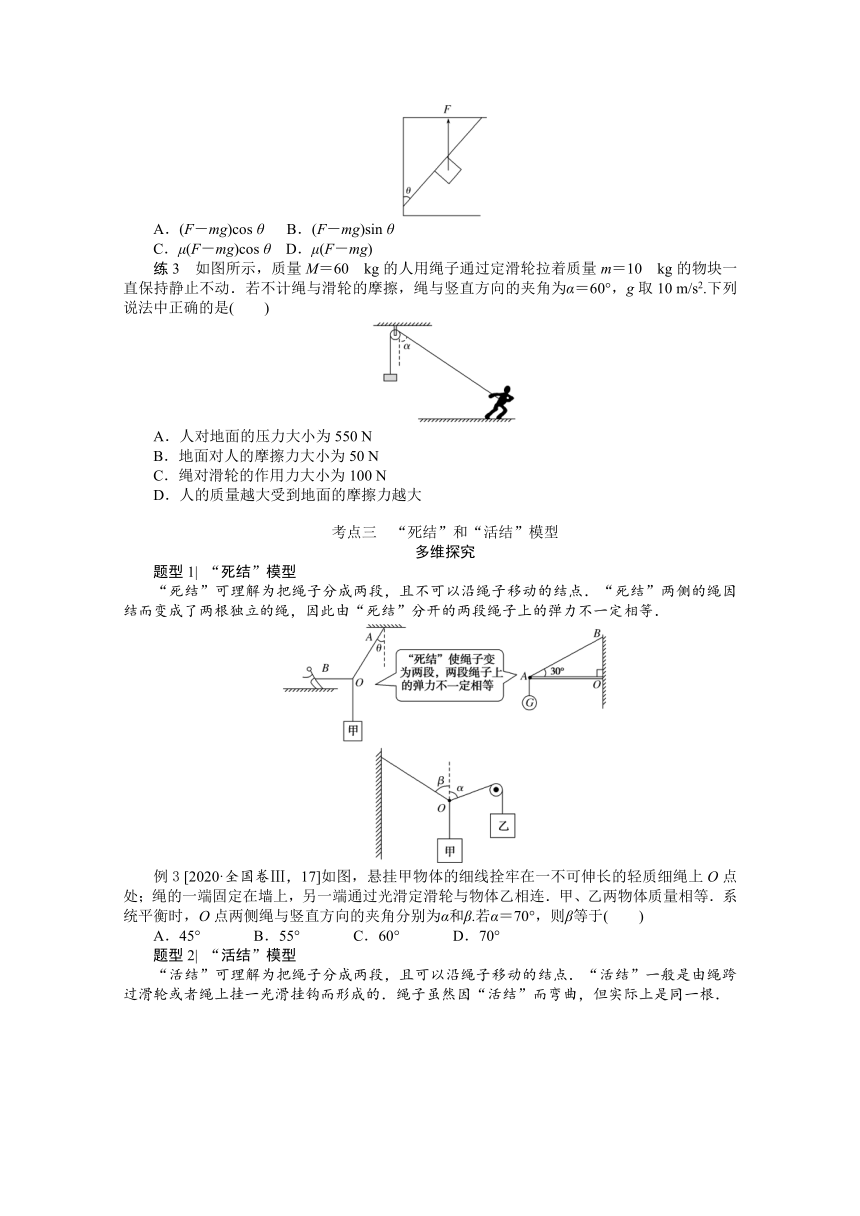
作用在物体的同一点,或作用线的________交于一点的几个力.如图所示均为共点力.
3.力的合成
(1)定义:求几个力的________的过程.
(2)运算法则
①平行四边形定则:求两个互成角度的分力的合力,可以用表示这两个力的线段为________作平行四边形,这两个邻边之间的________就表示合力的大小和方向.如图甲所示,F1、F2为分力,F为合力.
②三角形定则:把两个矢量的首尾顺次连接起来,第一个矢量的首到第二个矢量的尾的________________为合矢量.如图乙,F1、F2为分力,F为合力.
4.力的分解
(1)定义:求一个已知力的________的过程.
(2)遵循原则:____________定则或________定则.
(3)分解方法:①按力产生的________分解;②正交分解.
知识点二 矢量和标量
1.矢量:既有大小又有______的物理量,叠加时遵循__________定则,如速度、力等.
2.标量:只有大小没有______的物理量,求和时按________法则相加,如路程、速率等.
思考辨析
(1)合力与原来那几个力同时作用在物体上.( )
(2)合力一定时,两等大分力间的夹角θ越大,两分力越小.( )
(3)两个力的合力不可能比其分力小.( )
(4)对力分解时必须按作用效果分解.( )
(5)区别矢量与标量的根本是遵守的运算法则.( )
教材改编
1.[人教版必修1P64T2改编]有两个力,它们的合力为0.现在把其中一个向东6 N的力改为向南(大小不变),它们的合力大小为( )
A.6 N
B.62 N
C.12 N
D.0
2.[人教版必修1P66T2改编]一个竖直向下的180 N的力分解为两个分力,一个分力在水平方向上并等于240 N,则另一个分力的大小为( )
A.60 N
B.240 N
C.300 N
D.420 N
考点一 力的合成自主演练
1.两个共点力的合成
|F1-F2|≤F合≤F1+F2,即两个力大小不变时,其合力随夹角的增大而减小,当两力反向时,合力最小;当两力同向时,合力最大.
2.三个共点力的合成
(1)最大值:三个力共线且同向时,其合力最大,为F1+F2+F3.
(2)最小值:任取两个力,求出其合力的范围,如果第三个力在这个范围之内,则三个力的合力的最小值为零,如果第三个力不在这个范围内,则合力的最小值为最大的一个力减去另外两个较小的力的大小之和.
[多维练透]
1.[2020·宁夏银川市联考]如图所示,两人同时用大小相等的力沿不同方向拉小船,且两力关于小船轴线对称,下列几种情况中,合力最大的是( )
2.如图所示,某物体在四个共点力作用下处于平衡状态,若将F4=2 N的力沿逆时针方向转动90°,其余三个力的大小和方向不变,则此时物体所受合力的大小为( )
A.0 B.2 N C.22 N D. 2 N
3.[2021·邯郸模拟]在平面内有作用于同一点的四个力,以力的作用点为坐标原点O,四个力的方向如图所示,其中F1=6 N,F2=8 N,F3=4 N,F4=2 N.这四个力的合力方向指向( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.某物体同时受到2个共点力的作用,在如图所示的四种情况中(坐标纸中每格的边长均表示1 N大小的力),物体所受合外力最大的是( )
题后反思
(1)共点力合成的方法:
①作图法.
②计算法.
应用三角形中的边角关系求解.
(2)多个共点力的合成方法:
考点二 力的分解
师生共研
题型1|效果分解法
例1 (多选)明朝谢肇淛的《五杂组》中记载:“明姑苏虎丘寺塔倾侧,议欲正之,非万缗不可.一游僧见之曰:无烦也,我能正之.”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去,经月余扶正了塔身.假设所用的木楔为等腰三角形,木楔的顶角为θ,现在木楔背上加一力F,方向如图所示,木楔两侧产生推力FN,则( )
A.若F一定,θ大时FN大 B.若F一定,θ小时FN大
C.若θ一定,F大时FN大 D.若θ一定,F小时FN大
题后反思
力的效果分解法的步骤
题型2|正交分解法
例2 如图所示,一质量为m的沙袋用不可伸长的轻绳悬挂在支架上,一练功队员用垂直于绳的力将沙袋缓慢拉起,使绳与竖直方向的夹角为θ=30°,且绳绷紧,则练功队员对沙袋施加的作用力大小为( )
A. 12mg B. 32mg C. 33mg D. 3mg
题后反思
正交分解法的步骤
练1 [2020·肇庆模拟]如图所示,被轻绳系住静止在光滑斜面上的小球.若按力的实际作用效果来分解小球受到的重力G,则G的两个分力的方向分别是图中的( )
A.1和4 B.3和4
C.2和4 D.3和2
练2 如图所示,建筑装修中工人用质量为m的磨石对斜壁进行打磨,当对磨石施加竖直向上大小为F的推力时,磨石恰好沿斜壁向上匀速运动.已知磨石与斜壁之间的动摩擦因数为μ,斜壁与竖直方向的夹角为θ,则磨石受到的摩擦力是( )
A.(F-mg)cos θ B.(F-mg)sin θ
C.μ(F-mg)cos θ D.μ(F-mg)
练3 如图所示,质量M=60 kg的人用绳子通过定滑轮拉着质量m=10 kg的物块一直保持静止不动.若不计绳与滑轮的摩擦,绳与竖直方向的夹角为α=60°,g取10 m/s2.下列说法中正确的是( )
A.人对地面的压力大小为550 N
B.地面对人的摩擦力大小为50 N
C.绳对滑轮的作用力大小为100 N
D.人的质量越大受到地面的摩擦力越大
考点三 “死结”和“活结”模型
多维探究
题型1| “死结”模型
“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点.“死结”两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等.
例3 [2020·全国卷Ⅲ,17]如图,悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处;绳的一端固定在墙上,另一端通过光滑定滑轮与物体乙相连.甲、乙两物体质量相等.系统平衡时,O点两侧绳与竖直方向的夹角分别为α和β.若α=70°,则β等于( )
A.45° B.55° C.60° D.70°
题型2| “活结”模型
“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点.“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的.绳子虽然因“活结”而弯曲,但实际上是同一根.
例4 [2021·辽宁葫芦岛模拟]如图所示,细绳一端固定在A点,另一端跨过与A等高的光滑定滑轮B后悬挂一个砂桶Q(含砂子).现有另一个砂桶P(含砂子)通过光滑挂钩挂在A、B之间的细绳上,稳定后挂钩下降至C点,∠ACB=120°,下列说法正确的是( )
A.若只增加Q桶中的砂子,再次平衡后P桶位置不变
B.若只增加P桶中的砂子,再次平衡后P桶位置不变
C.若在两桶内增加相同质量的砂子,再次平衡后P桶位置不变
D.若在两桶内增加相同质量的砂子,再次平衡后Q桶位置上升
练4 [2016·全国卷Ⅲ,17]如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )
A. m2 B. 32m C.m D.2m
思维拓展
力的合成与分解在生产、生活中的应用(STSE问题)
例1 [生活]如图所示是山区村民用斧头劈柴的剖面图,图中BC边为斧头背面,AB、AC边是斧头的刃面.要使斧头容易劈开木柴,则应( )
A.缩短BC边,AB边也缩短些
B.BC边延长些,AB边缩短些
C.BC边缩短些,但AB边延长些
D.BC边延长些,AB边也延长些
例2 [体育]重力为G的体操运动员在进行自由体操比赛时,有如图所示的比赛动作,当运动员竖直倒立保持静止状态时,两手臂对称支撑,夹角为θ,则( )
A.当θ=60°时,运动员单手对地面的正压力大小为G2
B.当θ=120°时,运动员单手对地面的正压力大小为G
C.当θ不同时,运动员受到的合力不同
D.当θ不同时,运动员与地面之间的相互作用力不相等
例3 [科技][2020·安徽皖北协作区4月联考]航母阻拦索用于拦停高速着舰的舰载机,被喻为“舰载机生命线”.如图所示为其结构简图,滑轮1、2、3、4及液压缸a、b、c固定在甲板平面上,阻拦索绕过滑轮组后闭合.某时刻舰载机的挂钩勾住阻拦索,形成图示的夹角时,舰载机受到阻拦索的合力大小为F.不考虑阻拦索、滑轮的质量及一切摩擦,则此时单个柱塞所受阻拦索的合力大小为( )
A. F3 B. 3F3 C.F D. 3F
第2讲 力的合成与分解
基础落实
知识点一
1.(1)合力 分力 (2)等效替代
2.延长线
3.(1)合力
(2)①邻边 对角线 ②有向线段
4.(1)分力 (2)平行四边形 三角形
(3)效果
知识点二
1.方向 平行四边形
2.方向 代数
思考辨析
(1)× (2)× (3)× (4)× (5)√
教材改编
1.答案:B
2.答案:C
考点突破
1.解析:合力与分力的关系遵循平行四边形定则,两等大分力夹角越小,合力越大,故选项A正确.
答案:A
2.解析:物体在四个共点力作用下处于平衡状态,合力为零,F4的方向沿逆时针方向转过90°角,此时与其他三个力的合力大小相等,方向垂直,则物体受到的合力为F合=2F4=2 N,选项B正确,A、C、D错误.
答案:B
3.解析:F1=6 N,方向沿x轴的正向;F3=4 N,沿x轴负向;故F1与F3的合力F13沿着x轴的正方向,为2 N;F2=8 N,沿y轴正向;F4=2 N,沿y轴负向;故F2与F4的合力F24为6 N,沿着y轴正方向;最后再将F13与F24合成,故合力F1234为210 N,指向第一象限,选项A正确,B、C、D错误.
答案:A
4.解析:A图中,将F1与F2进行合成,求得合力的大小为F合=3 N,如图甲所示;B图中,将F1与F2进行合成,求得合力的大小为F合=32+42 N=5 N,如图乙所示;C图中,将F1与F2进行合成,求得合力的大小为F合=42 N,如图丙所示;D图中,将F1与F2进行合成,求得合力的大小为F合=3 N,如图丁所示,故选项C符合题意.
答案:C
例1 解析:选木楔为研究对象,木楔受到的力有:水平向左的力F和两侧给它的与木楔的斜面垂直的弹力,由于木楔处于平衡状态,所以两侧给它的与木楔的斜面垂直的弹力与F沿两侧分解的推力是相等的,力F的分解如图.
则F=FN1cos 90°-θ2+FN2cos 90°-θ2
=2FN1cos 90°-θ2=2FN1sin θ2,FN=FN1=FN2,
故解得FN=F2sinθ2,所以F一定时,θ越小,FN越大;θ一定时,F越大,FN越大,A、D错误,B、C正确.
答案:BC
例2
解析:如图,建立直角坐标系,对沙袋进行受力分析.由平衡条件有:F cos 30°-FTsin 30°=0,
FTcos 30°+F sin 30°-mg=0,联立可解得:F=12mg,选项A正确.
答案:A
练1 解析:小球的重力产生两个效果,一是使绳子拉伸,二是使斜面受压,故应按这两个方向分解,分别是3和4,故B正确,A、C、D错误.
答案:B
练2 解析:
分析磨石的受力情况,其受重力mg、弹力FN(垂直于斜壁向下)、摩擦力Ff(沿斜壁向下)、外力F四个力,沿斜壁和垂直于斜壁方向把这四个力正交分解,由于磨石处于平衡状态,在沿斜壁方向有mg cos θ+Ff=F cos θ,垂直于斜壁方向有FN+mg sin θ=F sin θ,Ff=μFN,则Ff=(F-mg)cos θ,选项A正确.
答案:A
练3 解析:绳子拉力总等于物块的重力100 N,则有T′=T=mg,对人和滑轮分别进行受力分析如图所示,可得人对地面的压力大小为N′=N=Mg-mg cos α=600 N-50 N=550 N,A正确;地面对人的摩擦力大小为f=mg sin α=100×32 N=503 N,B错误;对滑轮受力分析可得绳对滑轮的作用力大小为F=2mg cos α2=1003 N,C错误;改变人的质量,静摩擦力不变,D错误.
答案:A
例3
解析:O点受力如图
因为甲、乙物体质量相等
所以F1与F2大小相等,合成的平行四边形为菱形,α=70°,则∠1=∠2=55°
F1和F2的合力与F3等大反向,β=∠2,故B正确.
答案:B
例4 解析:对砂桶Q分析有,Q受到细绳的拉力大小FT=GQ,设AC、BC之间的夹角为θ,对C点分析可知C点受三个力而平衡,由题意知,C点两侧的绳张力相等,故有2FTcos θ2=GP,联立可得2GQ cos θ2=GP,故只增加Q桶中的砂子,即只增加GQ,夹角θ变大,P桶上升;只增加P桶中的砂子,即只增加GP,夹角θ变小,P桶下降,选项A、B错误;由2GQ cos θ2=GP可知,当θ=120°时有GQ=GP,此时若在两砂桶内增加相同质量的砂子,上式依然成立,则P桶的位置不变,选项C正确,D错误.
答案:C
练4
解析:如图所示,由于不计摩擦,线上张力处处相等,且轻环受细线的作用力的合力方向指向圆心.由于a、b间距等于圆弧半径,则∠aOb=60°,进一步分析知,细线与aO、bO间的夹角皆为30°.取悬挂的小物块研究,悬挂小物块的细线张角为120°,由平衡条件知,小物块的质量与小球的质量相等,即为m.故选项C正确.
答案:C
思维拓展
典例1 解析:如图所示,斧头劈柴的力形成对木柴两端的挤压力,两力与斧头的AB、AC边相互垂直;则可知当BC边缩短一些,AB边延长一些时两力之间的夹角更大,则两分力更大,更容易劈开木柴,故C正确.
答案:C
典例2 解析:运动员处于静止状态,即平衡状态,每只手都承受自身重力的一半,和角度无关,A正确,B、C错误;由牛顿第三定律知当θ不同时,运动员与地面间的相互作用力大小相等,D错误.
答案:A
误区警示:请注意审题:题目A、B两项问的是单手对地面的正压力即弹力的大小,故可用整体法直接快捷求解.
典例3 解析:某时刻舰载机的挂钩勾住阻拦索,形成图示的60°夹角,由于挂钩两侧阻拦索中拉力相等,由2F′cos 30°=F,解得阻拦索中的拉力F′=3F3.由于柱塞两侧阻拦索中拉力相等,其合力方向在两侧阻拦索拉力所成夹角的角平分线上,所以单个柱塞所受阻拦索的合力大小为F合=2F′cos 60°=F′=3F3,选项B正确.
答案:B
知识点一 力的合成
1.合力与分力
(1)定义:如果几个力共同作用产生的效果与一个力的作用效果相同,这一个力就叫做那几个力的________,那几个力叫做这一个力的________.
(2)关系:合力与分力是________________关系.
2.共点力
作用在物体的同一点,或作用线的________交于一点的几个力.如图所示均为共点力.
3.力的合成
(1)定义:求几个力的________的过程.
(2)运算法则
①平行四边形定则:求两个互成角度的分力的合力,可以用表示这两个力的线段为________作平行四边形,这两个邻边之间的________就表示合力的大小和方向.如图甲所示,F1、F2为分力,F为合力.
②三角形定则:把两个矢量的首尾顺次连接起来,第一个矢量的首到第二个矢量的尾的________________为合矢量.如图乙,F1、F2为分力,F为合力.
4.力的分解
(1)定义:求一个已知力的________的过程.
(2)遵循原则:____________定则或________定则.
(3)分解方法:①按力产生的________分解;②正交分解.
知识点二 矢量和标量
1.矢量:既有大小又有______的物理量,叠加时遵循__________定则,如速度、力等.
2.标量:只有大小没有______的物理量,求和时按________法则相加,如路程、速率等.
思考辨析
(1)合力与原来那几个力同时作用在物体上.( )
(2)合力一定时,两等大分力间的夹角θ越大,两分力越小.( )
(3)两个力的合力不可能比其分力小.( )
(4)对力分解时必须按作用效果分解.( )
(5)区别矢量与标量的根本是遵守的运算法则.( )
教材改编
1.[人教版必修1P64T2改编]有两个力,它们的合力为0.现在把其中一个向东6 N的力改为向南(大小不变),它们的合力大小为( )
A.6 N
B.62 N
C.12 N
D.0
2.[人教版必修1P66T2改编]一个竖直向下的180 N的力分解为两个分力,一个分力在水平方向上并等于240 N,则另一个分力的大小为( )
A.60 N
B.240 N
C.300 N
D.420 N
考点一 力的合成自主演练
1.两个共点力的合成
|F1-F2|≤F合≤F1+F2,即两个力大小不变时,其合力随夹角的增大而减小,当两力反向时,合力最小;当两力同向时,合力最大.
2.三个共点力的合成
(1)最大值:三个力共线且同向时,其合力最大,为F1+F2+F3.
(2)最小值:任取两个力,求出其合力的范围,如果第三个力在这个范围之内,则三个力的合力的最小值为零,如果第三个力不在这个范围内,则合力的最小值为最大的一个力减去另外两个较小的力的大小之和.
[多维练透]
1.[2020·宁夏银川市联考]如图所示,两人同时用大小相等的力沿不同方向拉小船,且两力关于小船轴线对称,下列几种情况中,合力最大的是( )
2.如图所示,某物体在四个共点力作用下处于平衡状态,若将F4=2 N的力沿逆时针方向转动90°,其余三个力的大小和方向不变,则此时物体所受合力的大小为( )
A.0 B.2 N C.22 N D. 2 N
3.[2021·邯郸模拟]在平面内有作用于同一点的四个力,以力的作用点为坐标原点O,四个力的方向如图所示,其中F1=6 N,F2=8 N,F3=4 N,F4=2 N.这四个力的合力方向指向( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.某物体同时受到2个共点力的作用,在如图所示的四种情况中(坐标纸中每格的边长均表示1 N大小的力),物体所受合外力最大的是( )
题后反思
(1)共点力合成的方法:
①作图法.
②计算法.
应用三角形中的边角关系求解.
(2)多个共点力的合成方法:
考点二 力的分解
师生共研
题型1|效果分解法
例1 (多选)明朝谢肇淛的《五杂组》中记载:“明姑苏虎丘寺塔倾侧,议欲正之,非万缗不可.一游僧见之曰:无烦也,我能正之.”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去,经月余扶正了塔身.假设所用的木楔为等腰三角形,木楔的顶角为θ,现在木楔背上加一力F,方向如图所示,木楔两侧产生推力FN,则( )
A.若F一定,θ大时FN大 B.若F一定,θ小时FN大
C.若θ一定,F大时FN大 D.若θ一定,F小时FN大
题后反思
力的效果分解法的步骤
题型2|正交分解法
例2 如图所示,一质量为m的沙袋用不可伸长的轻绳悬挂在支架上,一练功队员用垂直于绳的力将沙袋缓慢拉起,使绳与竖直方向的夹角为θ=30°,且绳绷紧,则练功队员对沙袋施加的作用力大小为( )
A. 12mg B. 32mg C. 33mg D. 3mg
题后反思
正交分解法的步骤
练1 [2020·肇庆模拟]如图所示,被轻绳系住静止在光滑斜面上的小球.若按力的实际作用效果来分解小球受到的重力G,则G的两个分力的方向分别是图中的( )
A.1和4 B.3和4
C.2和4 D.3和2
练2 如图所示,建筑装修中工人用质量为m的磨石对斜壁进行打磨,当对磨石施加竖直向上大小为F的推力时,磨石恰好沿斜壁向上匀速运动.已知磨石与斜壁之间的动摩擦因数为μ,斜壁与竖直方向的夹角为θ,则磨石受到的摩擦力是( )
A.(F-mg)cos θ B.(F-mg)sin θ
C.μ(F-mg)cos θ D.μ(F-mg)
练3 如图所示,质量M=60 kg的人用绳子通过定滑轮拉着质量m=10 kg的物块一直保持静止不动.若不计绳与滑轮的摩擦,绳与竖直方向的夹角为α=60°,g取10 m/s2.下列说法中正确的是( )
A.人对地面的压力大小为550 N
B.地面对人的摩擦力大小为50 N
C.绳对滑轮的作用力大小为100 N
D.人的质量越大受到地面的摩擦力越大
考点三 “死结”和“活结”模型
多维探究
题型1| “死结”模型
“死结”可理解为把绳子分成两段,且不可以沿绳子移动的结点.“死结”两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等.
例3 [2020·全国卷Ⅲ,17]如图,悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O点处;绳的一端固定在墙上,另一端通过光滑定滑轮与物体乙相连.甲、乙两物体质量相等.系统平衡时,O点两侧绳与竖直方向的夹角分别为α和β.若α=70°,则β等于( )
A.45° B.55° C.60° D.70°
题型2| “活结”模型
“活结”可理解为把绳子分成两段,且可以沿绳子移动的结点.“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的.绳子虽然因“活结”而弯曲,但实际上是同一根.
例4 [2021·辽宁葫芦岛模拟]如图所示,细绳一端固定在A点,另一端跨过与A等高的光滑定滑轮B后悬挂一个砂桶Q(含砂子).现有另一个砂桶P(含砂子)通过光滑挂钩挂在A、B之间的细绳上,稳定后挂钩下降至C点,∠ACB=120°,下列说法正确的是( )
A.若只增加Q桶中的砂子,再次平衡后P桶位置不变
B.若只增加P桶中的砂子,再次平衡后P桶位置不变
C.若在两桶内增加相同质量的砂子,再次平衡后P桶位置不变
D.若在两桶内增加相同质量的砂子,再次平衡后Q桶位置上升
练4 [2016·全国卷Ⅲ,17]如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )
A. m2 B. 32m C.m D.2m
思维拓展
力的合成与分解在生产、生活中的应用(STSE问题)
例1 [生活]如图所示是山区村民用斧头劈柴的剖面图,图中BC边为斧头背面,AB、AC边是斧头的刃面.要使斧头容易劈开木柴,则应( )
A.缩短BC边,AB边也缩短些
B.BC边延长些,AB边缩短些
C.BC边缩短些,但AB边延长些
D.BC边延长些,AB边也延长些
例2 [体育]重力为G的体操运动员在进行自由体操比赛时,有如图所示的比赛动作,当运动员竖直倒立保持静止状态时,两手臂对称支撑,夹角为θ,则( )
A.当θ=60°时,运动员单手对地面的正压力大小为G2
B.当θ=120°时,运动员单手对地面的正压力大小为G
C.当θ不同时,运动员受到的合力不同
D.当θ不同时,运动员与地面之间的相互作用力不相等
例3 [科技][2020·安徽皖北协作区4月联考]航母阻拦索用于拦停高速着舰的舰载机,被喻为“舰载机生命线”.如图所示为其结构简图,滑轮1、2、3、4及液压缸a、b、c固定在甲板平面上,阻拦索绕过滑轮组后闭合.某时刻舰载机的挂钩勾住阻拦索,形成图示的夹角时,舰载机受到阻拦索的合力大小为F.不考虑阻拦索、滑轮的质量及一切摩擦,则此时单个柱塞所受阻拦索的合力大小为( )
A. F3 B. 3F3 C.F D. 3F
第2讲 力的合成与分解
基础落实
知识点一
1.(1)合力 分力 (2)等效替代
2.延长线
3.(1)合力
(2)①邻边 对角线 ②有向线段
4.(1)分力 (2)平行四边形 三角形
(3)效果
知识点二
1.方向 平行四边形
2.方向 代数
思考辨析
(1)× (2)× (3)× (4)× (5)√
教材改编
1.答案:B
2.答案:C
考点突破
1.解析:合力与分力的关系遵循平行四边形定则,两等大分力夹角越小,合力越大,故选项A正确.
答案:A
2.解析:物体在四个共点力作用下处于平衡状态,合力为零,F4的方向沿逆时针方向转过90°角,此时与其他三个力的合力大小相等,方向垂直,则物体受到的合力为F合=2F4=2 N,选项B正确,A、C、D错误.
答案:B
3.解析:F1=6 N,方向沿x轴的正向;F3=4 N,沿x轴负向;故F1与F3的合力F13沿着x轴的正方向,为2 N;F2=8 N,沿y轴正向;F4=2 N,沿y轴负向;故F2与F4的合力F24为6 N,沿着y轴正方向;最后再将F13与F24合成,故合力F1234为210 N,指向第一象限,选项A正确,B、C、D错误.
答案:A
4.解析:A图中,将F1与F2进行合成,求得合力的大小为F合=3 N,如图甲所示;B图中,将F1与F2进行合成,求得合力的大小为F合=32+42 N=5 N,如图乙所示;C图中,将F1与F2进行合成,求得合力的大小为F合=42 N,如图丙所示;D图中,将F1与F2进行合成,求得合力的大小为F合=3 N,如图丁所示,故选项C符合题意.
答案:C
例1 解析:选木楔为研究对象,木楔受到的力有:水平向左的力F和两侧给它的与木楔的斜面垂直的弹力,由于木楔处于平衡状态,所以两侧给它的与木楔的斜面垂直的弹力与F沿两侧分解的推力是相等的,力F的分解如图.
则F=FN1cos 90°-θ2+FN2cos 90°-θ2
=2FN1cos 90°-θ2=2FN1sin θ2,FN=FN1=FN2,
故解得FN=F2sinθ2,所以F一定时,θ越小,FN越大;θ一定时,F越大,FN越大,A、D错误,B、C正确.
答案:BC
例2
解析:如图,建立直角坐标系,对沙袋进行受力分析.由平衡条件有:F cos 30°-FTsin 30°=0,
FTcos 30°+F sin 30°-mg=0,联立可解得:F=12mg,选项A正确.
答案:A
练1 解析:小球的重力产生两个效果,一是使绳子拉伸,二是使斜面受压,故应按这两个方向分解,分别是3和4,故B正确,A、C、D错误.
答案:B
练2 解析:
分析磨石的受力情况,其受重力mg、弹力FN(垂直于斜壁向下)、摩擦力Ff(沿斜壁向下)、外力F四个力,沿斜壁和垂直于斜壁方向把这四个力正交分解,由于磨石处于平衡状态,在沿斜壁方向有mg cos θ+Ff=F cos θ,垂直于斜壁方向有FN+mg sin θ=F sin θ,Ff=μFN,则Ff=(F-mg)cos θ,选项A正确.
答案:A
练3 解析:绳子拉力总等于物块的重力100 N,则有T′=T=mg,对人和滑轮分别进行受力分析如图所示,可得人对地面的压力大小为N′=N=Mg-mg cos α=600 N-50 N=550 N,A正确;地面对人的摩擦力大小为f=mg sin α=100×32 N=503 N,B错误;对滑轮受力分析可得绳对滑轮的作用力大小为F=2mg cos α2=1003 N,C错误;改变人的质量,静摩擦力不变,D错误.
答案:A
例3
解析:O点受力如图
因为甲、乙物体质量相等
所以F1与F2大小相等,合成的平行四边形为菱形,α=70°,则∠1=∠2=55°
F1和F2的合力与F3等大反向,β=∠2,故B正确.
答案:B
例4 解析:对砂桶Q分析有,Q受到细绳的拉力大小FT=GQ,设AC、BC之间的夹角为θ,对C点分析可知C点受三个力而平衡,由题意知,C点两侧的绳张力相等,故有2FTcos θ2=GP,联立可得2GQ cos θ2=GP,故只增加Q桶中的砂子,即只增加GQ,夹角θ变大,P桶上升;只增加P桶中的砂子,即只增加GP,夹角θ变小,P桶下降,选项A、B错误;由2GQ cos θ2=GP可知,当θ=120°时有GQ=GP,此时若在两砂桶内增加相同质量的砂子,上式依然成立,则P桶的位置不变,选项C正确,D错误.
答案:C
练4
解析:如图所示,由于不计摩擦,线上张力处处相等,且轻环受细线的作用力的合力方向指向圆心.由于a、b间距等于圆弧半径,则∠aOb=60°,进一步分析知,细线与aO、bO间的夹角皆为30°.取悬挂的小物块研究,悬挂小物块的细线张角为120°,由平衡条件知,小物块的质量与小球的质量相等,即为m.故选项C正确.
答案:C
思维拓展
典例1 解析:如图所示,斧头劈柴的力形成对木柴两端的挤压力,两力与斧头的AB、AC边相互垂直;则可知当BC边缩短一些,AB边延长一些时两力之间的夹角更大,则两分力更大,更容易劈开木柴,故C正确.
答案:C
典例2 解析:运动员处于静止状态,即平衡状态,每只手都承受自身重力的一半,和角度无关,A正确,B、C错误;由牛顿第三定律知当θ不同时,运动员与地面间的相互作用力大小相等,D错误.
答案:A
误区警示:请注意审题:题目A、B两项问的是单手对地面的正压力即弹力的大小,故可用整体法直接快捷求解.
典例3 解析:某时刻舰载机的挂钩勾住阻拦索,形成图示的60°夹角,由于挂钩两侧阻拦索中拉力相等,由2F′cos 30°=F,解得阻拦索中的拉力F′=3F3.由于柱塞两侧阻拦索中拉力相等,其合力方向在两侧阻拦索拉力所成夹角的角平分线上,所以单个柱塞所受阻拦索的合力大小为F合=2F′cos 60°=F′=3F3,选项B正确.
答案:B
同课章节目录
