2020-2021学年 高一物理 运动图象 追及相遇问题 期末复习强化学案Word版含答案
文档属性
| 名称 | 2020-2021学年 高一物理 运动图象 追及相遇问题 期末复习强化学案Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 821.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-14 13:30:12 | ||
图片预览



文档简介
运动图象 追及相遇问题
考点一 运动图象的理解
自主演练
1.直线运动的x ? t图象
(1)意义:反映了直线运动的物体位移随时间变化的规律.
(2)图线上某点切线的斜率的意义
①斜率大小:表示物体速度的大小.
②斜率的正负:表示物体速度的方向.
(3)两种特殊的x ? t图象.
①若x ? t图象是一条平行于时间轴的直线,说明物体处于静止状态.(如图甲所示).
②若x ? t的图象是一条倾斜的直线,说明物体在做匀速直线运动.(如图乙所示).
2.直线运动的v ? t图象
(1)意义:反映了直线运动的物体速度随时间变化的规律.
(2)图线上某点切线的斜率的意义
①斜率的大小:表示物体加速度的大小.
②斜率的正负:表示物体加速度的方向.
(3)两种特殊的v ? t图象
①匀速直线运动的v ? t图象是与横轴平行的直线.(如图甲所示)
②匀变速直线运动的v ? t图象是一条倾斜的直线.(如图乙所示)
(4)图线与坐标轴围成的“面积”的意义
①图线与坐标轴围成的“面积”表示相应时间的位移.
②若此面积在时间轴的上方,表示这段时间内的位移方向为正方向;若此面积在时间轴的下方,表示这段时间内的位移方向为负方向.
[多维练透]
1.A、B两物体沿同一直线运动,运动过程中的x ? t图象如图所示,下列说法正确的是( )
A.4 s时A物体运动方向发生改变
B.0~6 s内B物体的速度逐渐减小
C.0~5 s内两物体的平均速度相等
D.0~6 s内某时刻两物体的速度大小相等
2.下列所给的运动图象中能反映做直线运动的物体不会回到初始位置的是( )
3.下图甲为发射模型火箭的示意图,已知模型火箭质量m=1 kg,图乙为该段时间内火箭运动的v ? t图,关于火箭受力情况和运动情况,下列说法正确的是( )
A.火箭2 s时达到最高点
B.火箭在3 s时加速度的方向改变
C.火箭在1 s时和5 s时的加速度相同
D.火箭在4 s时位于发射点下方2 m处
考点二 运动图象的应用
师生共研
1.运用运动图象解题时的“六看”
x?t图象
v?t图象
纵截距
表示初位置
表示初速度
斜直线
表示匀速直线运动
表示匀变速直线运动
斜率
表示速度
表示加速度
面积
无实际意义
图线和时间轴围成的面积表示位移
交点
相遇点
速度相等点(临界条件点)
拐点
表示从一种运动变为另一种运动
表示从一种运动变为另一种运动
2.三点说明
(1)无论是x?t图象还是v?t图象都只能描述直线运动.
(2)x?t图象和v?t图象不表示物体运动的轨迹.
(3)x?t图象和v?t图象的形状由x与t、v与t的函数关系决定.
题型1 x?t图象的应用
例1 [2020·河北石家庄二中期末]甲、乙两车在同一条直线上行驶,它们运动的位移x随时间t变化的关系如图所示,已知乙车做匀变速直线运动,其图线与t轴相切于10 s处,则下列说法正确的是( )
A.甲车的初速度为零
B.乙车的初位置在x0=60 m处
C.乙车的加速度大小为1.6 m/s2
D.5 s时两车相遇,此时甲车速度较大
题型2 v?t图象的应用
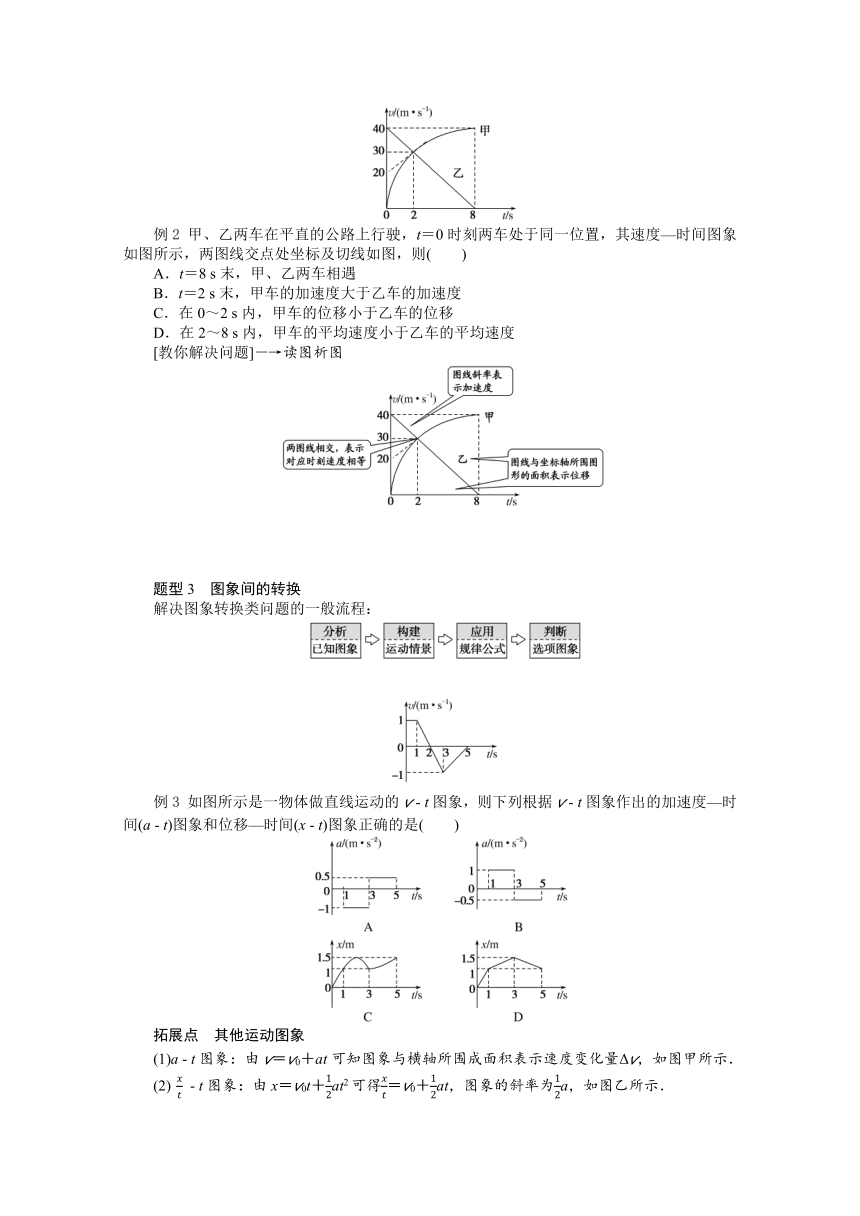
例2 甲、乙两车在平直的公路上行驶,t=0时刻两车处于同一位置,其速度—时间图象如图所示,两图线交点处坐标及切线如图,则( )
A.t=8 s末,甲、乙两车相遇
B.t=2 s末,甲车的加速度大于乙车的加速度
C.在0~2 s内,甲车的位移小于乙车的位移
D.在2~8 s内,甲车的平均速度小于乙车的平均速度
[教你解决问题]―→读图析图
题型3 图象间的转换
解决图象转换类问题的一般流程:
例3 如图所示是一物体做直线运动的v ? t图象,则下列根据v ? t图象作出的加速度—时间(a ? t)图象和位移—时间(x ? t)图象正确的是( )
拓展点 其他运动图象
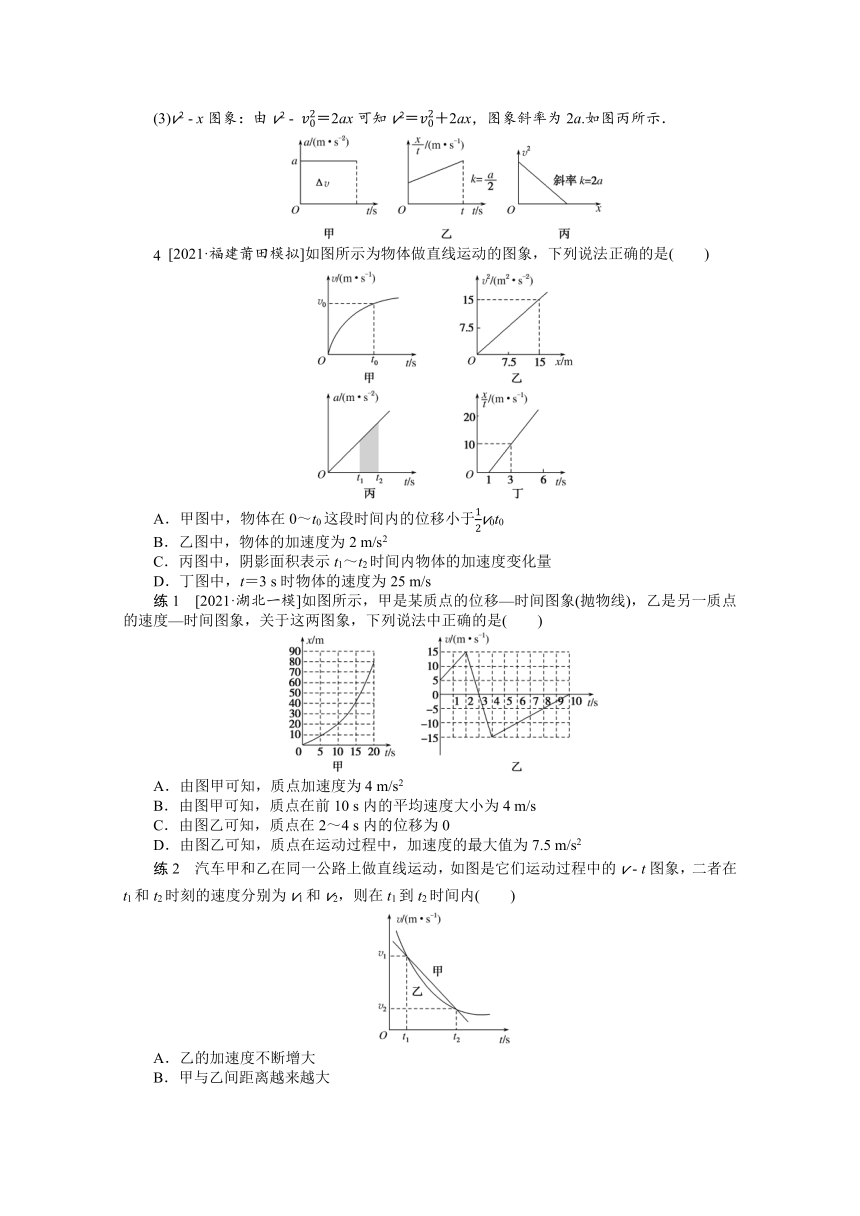
(1)a ? t图象:由v=v0+at可知图象与横轴所围成面积表示速度变化量Δv,如图甲所示.
(2) xt ? t图象:由x=v0t+12at2可得xt=v0+12at,图象的斜率为12a,如图乙所示.
(3)v2 ? x图象:由v2 ? v02=2ax可知v2=v02+2ax,图象斜率为2a.如图丙所示.
[2021·福建莆田模拟]如图所示为物体做直线运动的图象,下列说法正确的是( )
A.甲图中,物体在0~t0这段时间内的位移小于12v0t0
B.乙图中,物体的加速度为2 m/s2
C.丙图中,阴影面积表示t1~t2时间内物体的加速度变化量
D.丁图中,t=3 s时物体的速度为25 m/s
练1 [2021·湖北一模]如图所示,甲是某质点的位移—时间图象(抛物线),乙是另一质点的速度—时间图象,关于这两图象,下列说法中正确的是( )
A.由图甲可知,质点加速度为4 m/s2
B.由图甲可知,质点在前10 s内的平均速度大小为4 m/s
C.由图乙可知,质点在2~4 s内的位移为0
D.由图乙可知,质点在运动过程中,加速度的最大值为7.5 m/s2
练2 汽车甲和乙在同一公路上做直线运动,如图是它们运动过程中的v ? t图象,二者在t1和t2时刻的速度分别为v1和v2,则在t1到t2时间内( )
A.乙的加速度不断增大
B.甲与乙间距离越来越大
C.乙的平均速度vD.t1时刻甲的加速度大于乙的加速度
练3 [2021·湖北荆门联考]A、B两小车在同一直线上运动,它们运动的位移s随时间t变化的关系如图所示,已知A车的s ? t图线为抛物线的一部分,图线的最高点在第7 s末,B车的s ? t图线为直线,则下列说法正确的是( )
A.A车的初速度为7 m/s
B.A车的加速度大小为2 m/s2
C.A车减速过程运动的位移大小为50 m
D.10 s末两车相遇时,B车的速度较大
题后反思
图象问题求解策略
考点三 追及和相遇问题
多维探究
题型1 |追及相遇问题常用的分析方法
1.分析技巧:可概括为“一个临界条件”“两个关系”.
2.能否追上的判断方法
物体B追赶物体A:开始时,两个物体相距x0,到vA=vB时,若xA+x0xB,则不能追上.
3.特别提醒
若被追赶的物体做匀减速直线运动,一定要注意判断被追上前该物体是否已经停止运动.
例5 汽车A以vA=4 m/s的速度向右做匀速直线运动,汽车B以vB=10 m/s的速度同向运动,B在A前方x0=7 m处时汽车B开始匀减速刹车,直到静止后保持不动,B刹车的加速度大小a=2 m/s2,从汽车B开始刹车时计时.求:
(1)A追上B前,A、B间的最远距离是多少;
(2)经过多长时间A恰好追上B.
[教你解决问题]―→读题画过程示意图
题型2 与运动图象相结合的追及相遇问题
例6 [2021·武汉模拟]一辆汽车在平直的公路上匀速行驶,司机突然发现前方有一辆老年代步车正在慢速行驶,短暂反应后司机立即采取制动措施,结果汽车恰好没有撞上前方的老年代步车,若司机发现代步车时开始计时(t=0),两车的v ? t图象如图所示,则( )
A.图象中的a表示汽车,b表示老年代步车
B.汽车制动时的加速度大小为4.4 m/s2
C.从司机发现代步车到两车速度相等时经历的时间为3.0 s
D.司机发现代步车时汽车距离代步车30 m
练4 [2021·广州二调改编](多选)如图所示,图甲为质点a和b做直线运动的位移—时间(x ? t)图象,图乙为质点c和d做直线运动的速度—时间(v ? t)图象,由图可知( )
A.若t1时刻a、b两质点第一次相遇,则t2时刻两质点第二次相遇
B.若t1时刻c、d两质点第一次相遇,则t2时刻两质点第二次相遇
C.t1到t2时间内,b和d两个质点的运动方向发生了改变
D.t1到t2时间内,b和d两个质点的速度先减小后增大
练5 一步行者以6.0 m/s的速度跑去追赶被红灯阻停的公共汽车,在跑到距汽车25 m处时,绿灯亮了,汽车以1.0 m/s2的加速度匀加速启动前进,则( )
A.人能追上公共汽车,追赶过程中人跑了36 m
B.人不能追上公共汽车,人、车最近距离为7 m
C.人能追上公共汽车,追上车前人共跑了43 m
D.人不能追上公共汽车,且车开动后,人车距离越来越远
练6 A、B两辆列车在能见度很低的雾天里在同一轨道上同向行驶,A车在前,速度vA=10 m/s,B车在后,速度vB=30 m/s.当B车发现A车时就立刻刹车.已知B车在进行刹车测试时发现,若车以30 m/s的速度行驶时,刹车后至少要前进1 800 m才能停下,假设B车刹车过程中加速度恒定.为保证两辆列车不相撞,则能见度至少要达到( )
A.400 m B.600 m
C.800 m D.1 600 m
题后反思
追及相遇问题的解题流程
思维拓展
生活中多体多过程的运动学问题
题型1 体育+多体多过程问题
(多选)甲、乙两名运动员同时从泳池的两端出发,在泳池里训练,甲、乙的速度—时间图象分别如图(a)、(b)所示,不计转向的时间,两人的运动均可视为质点的直线运动.则( )
A.游泳池长25 m
B.经过1 min两人共相遇了3次
C.经过2 min两人共相遇了5次
D.两人一定不会在泳池的一端相遇
题型2 |交通+多体多过程问题
例2 为提高通行效率,许多高速公路出入口安装了电子不停车收费系统ETC.甲、乙两辆汽车分别通过ETC通道和人工收费通道(MTC)驶离高速公路,流程如图所示.假设减速带离收费岛口x=60 m,收费岛总长度d=40 m,两辆汽车同时以相同的速度v1=72 km/h经过减速带后,一起以相同的加速度做匀减速运动.甲车减速至v2=36 km/h后,匀速行驶到中心线即可完成缴费,自动栏杆打开放行;乙车刚好到收费岛中心线收费窗口停下,经过t0=15 s的时间缴费成功,人工栏杆打开放行.随后两辆汽车匀加速到速度v1后沿直线匀速行驶,设加速和减速过程中的加速度大小相等,求:
(1)此次人工收费通道和ETC通道打开栏杆放行的时间差;
(2)两辆汽车驶离收费站后相距的最远距离.
练1 [2021·湖北黄冈新起点考试]一辆从高速公路服务区驶出的小汽车甲以90 km/h的速度并入高速公路行车道向前行驶,甲车司机突然发现前方约100 m处有一辆正打开双闪的小汽车乙,以约45 km/h的速度缓慢行驶,此时甲车司机发现无法变道,经3 s的反应时间开始刹车,刹车加速度大小约为5 m/s2,则两车相距最近的距离约为( )
A.15 m B.53 m C.47 m D.63 m
练2 [2020·山东济南外国语学校5月月考]十一放假期间,全国高速公路对七座及以下小型客车免费放行,小轿车可以不停车通过收费站,但要求小轿车通过收费站窗口前x0=9 m区间的速度不超过v0=6 m/s.现在甲、乙两小轿车在收费站前平直公路上分别以v甲=20 m/s和v乙=34 m/s的速度匀速行驶,甲车在前,乙车在后.甲车司机发现正前方收费站,开始以大小为a甲=2 m/s2的加速度匀减速刹车.
(1)甲车司机需在离收费站窗口至少多远处开始刹车才不违章?
(2)若甲车司机经刹车到达离收费站窗口前9 m处的速度恰好为6 m/s,乙车司机在发现甲车刹车时经t0=0.5 s的反应时间后,开始以大小为a乙=4 m/s2的加速度匀减速刹车.为避免两车相撞,且乙车在收费站窗口前9 m区间不超速,则在甲车司机开始刹车时,甲、乙两车至少相距多远?
专题一 运动图象 追及相遇问题
考点突破
1.解析:A图线的斜率不变,则A物体的速度大小和方向不变,故A项错误;0~6 s内B物体图线切线的斜率增大,则B物体的速度逐渐增大,故B项错误;根据物体的位移Δx=x2-x1,可知0~5 s内,A物体的位移比B物体的大,则A物体的平均速度比B物体的大,故C项错误;0~6 s内B物体的图象切线斜率绝对值先小于A,后大于A,可知某时刻两物体的速度大小相等,故D项正确.
答案:D
2.解析:速度—时间图象中与坐标轴围成的面积表示位移,在坐标轴上方表示正位移,在坐标轴下方表示负位移,所以A项中面积不为零,位移不为零,物体不能回到初始位置;B、C两项中面积为零,位移为零,物体回到初始位置;位移—时间图象表示物体的位移随时间变化的图象,在t0时刻物体的位移为零,即物体又回到了初始位置.综上所述,A项正确.
答案:A
3.解析:2 s前后,运动方向不变,A项错误;3 s前后,v ? t图象的单调性不变,加速度方向不变,B项错误;由a=v-v0t得0~2 s内加速度a1=2 m/s2,4~6 s内加速度a2=2 m/s2,C项正确;0~3 s,v ? t图线所围面积x1=6 m,3~4 s,v ? t图线所围面积x2=-2 m,总位移为+4 m,表明火箭在4 s时位于发射点上方4 m处,D项错误.
答案:C
例1 解析:本题考查位移—时间图象.x ? t图线的斜率表示速度,则知甲车的速度不变,做匀速直线运动,初速度不为零,故A错误;甲车的速度v甲=ΔxΔt=205 m/s=4 m/s,乙车做匀变速直线运动,其图线与t轴相切于10 s处,则t=10 s时,乙车的速度为零,反过来看成乙车做初速度为零的匀加速直线运动,则有x=12at2,根据题图可知,20 m=12a·(5 s)2,解得乙车的加速度大小a=1.6 m/s2,则x0=80 m,故B错误,C正确;5 s时两车相遇,此时乙车的速度v乙=1.6×5 m/s=8 m/s,则乙车的速度较大,故D错误.
答案:C
例2 解析:根据速度—时间图线与坐标轴所围图形的面积表示位移可知,在0~8 s时间内,甲车的位移大于乙车的位移,又两车的初始位置相同,故t=8 s末,甲车在乙车前面,选项A错误;根据速度—时间图线的斜率表示加速度可知,在t=2 s时,甲车的加速度大小a1=5 m/s2,乙车的加速度大小a2=5 m/s2,甲、乙两车加速度大小相等,选项B错误;根据速度—时间图线与坐标轴所围图形的面积表示位移可知,在0~2 s时间内,甲车的位移小于乙车的位移,选项C正确;在2~8 s时间内,甲车的位移大于乙车的位移,根据平均速度公式可知,甲车的平均速度大于乙车的平均速度,选项D错误.
答案:C
例3 解析:由v ? t图象知,0~1 s内,物体做匀速直线运动,加速度a1=0,位移x=vt,x与t成正比;1~3 s内,物体的加速度不变,做匀变速直线运动,加速度a2=-1 m/s2,位移为x=v0(t-1 s)+12a2(t-1 s)2=-12t2+2t-32m,可知x ? t图象是开口向下的抛物线;3~5 s内,物体沿负方向做匀减速直线运动,加速度a3=0.5 m/s2,位移为x=-v0(t-3 s)+12a3(t-3 s)2,x ? t图象是开口向上的抛物线,且3~5 s内物体的位移为-1 m,由数学知识知,只有A选项对应的图象正确.
答案:A
例4 解析:由v ? t图线与坐标轴围成的面积表示位移,可知甲图中,物体在0~t0这段时间内的位移大于12v0t0(平均速度大于12v0),选项A错误;根据v2=2ax可知乙图中,2a=1 m/s2,则物体的加速度为0.5 m/s2,选项B错误;根据Δv=at可知,丙图中阴影部分的面积表示t1~t2时间内物体的速度变化量,选项C错误;由x=v0t+12at2可得xt=v0+12at,结合丁图可知12a=102 m/s2=5 m/s2(a前面的12易被忽视),即a=10 m/s2,则v0=-5 m/s,故t=3 s时物体的速度为v3=(-5+10×3) m/s=25 m/s,选项D正确.
答案:D
练1 解析:由图甲可知,x=12at2,取t=10 s,x=20 m,解得a=0.4 m/s2,质点在前10 s内的平均速度v=xt=2010 m/s=2 m/s,故A、B两项错误;由图乙可知,在2~4 s内,时间轴上方和下方的面积抵消,总位移为0,故C项正确;质点在运动过程中,加速度的最大值出现在2~4 s内,最大加速度大小为a=ΔvΔt=151 m/s2=15 m/s2,故D项错误.
答案:C
练2 解析:v ? t图象的斜率等于物体的加速度的大小,由图象知乙运动的加速度不断减小,t1时刻甲的加速度小于乙的加速度,选项A、D错误;由于不知道甲、乙初始位置关系,故无法判断二者间距离如何变化,选项B错误;乙在t1和t2时间内的位移小于做匀减速直线运动的位移,故平均速度v答案:C
练3 解析:本题考查匀变速直线运动与匀速直线运动的位移—时间图象的关系.A车做匀变速直线运动,设A车的初速度为v0,加速度大小为a,由题图可知,t=7 s时,速度为零,由运动学公式可得v7=v0-7a=0,根据图象和运动学公式可知,t′=10 s时的位移x10=40 m,x10=v0t′-12at′2=10v0-50a(m),联立解得a=2 m/s2,v0=14 m/s,故A错误,B正确;A车减速过程运动的位移大小x7=v0+02t=0+142×7 m=49 m,故C错误;位移—时间图线的斜率等于速度,10 s末两车相遇时B车的速度大小vB=ΔxΔt=4 m/s,A车的速度vA=v0-at′=-6 m/s,则A车的速度大于B车的速度,故D错误.
答案:B
例5 解析:(1)当A、B两汽车速度相等时,两车间的距离最远,此时有
v=vB-at=vA,解得t=3 s
此过程中汽车A的位移xA=vAt=12 m
汽车B的位移xB=vBt-12at2=21 m
故最远距离Δxmax=xB+x0-xA=16 m.
(2)汽车B从开始减速直到静止经历的时间t1=vBa=5 s
运动的位移x′B=vB22a=25 m
汽车A在t1时间内运动的位移x′A=vAt1=20 m
此时两车相距Δx=x′B+x0-x′A=12 m
汽车A需再运动的时间t2=ΔxvA=3 s
故A追上B所用时间t总=t1+t2=8 s.
答案:(1)16 m (2)8 s
例6 解析:汽车制动后速度减小,则知图象中的a表示老年代步车,b表示汽车,故A项错误;汽车制动时的加速度大小为a=ΔvΔt=204.5-0.5m/s2=5 m/s2,故B错误;设从汽车制动到两车速度相等时经历的时间为t,则va=vb-at,得t=va-vba=20-55 s=3 s,所以从司机发现代步车到两车速度相等时经历的时间为t′=t+0.5 s=3.5 s,故C项错误;汽车恰好没有撞上前方老年代步车的时刻是t=3.5 s,根据图线与坐标轴围成的面积表示位移大小,知司机发现代步车时汽车与代步车的距离s=0.5+3.52×15 m=30 m,故D项正确.
答案:D
练4 解析:位移—时间图象中两图线的交点表示两者相遇,根据图甲可知,选项A正确;速度—时间图象中两图线的交点表示两者速度相等,根据图乙可知,选项B错误;位移—时间图线斜率的正负表示运动方向,根据图甲可知,t1到t2时间内质点b的运动方向发生改变.速度—时间图线在t轴上方表示速度方向为正,根据图乙可知,t1到t2时间内质点d的运动方向不变,选项C错误;位移—时间图线的斜率表示速度,根据图甲可知,t1到t2时间内,质点b的速度先减小后增大.根据图乙可知,t1到t2时间内,质点d速度先减小后增大,选项D正确.
答案:AD
练5 解析:在跑到距汽车25 m处时,绿灯亮了,汽车以1.0 m/s2的加速度匀加速启动前进,当汽车加速到6.0 m/s时二者相距最近.汽车加速到6.0 m/s所用时间t=6 s,人运动距离为6×6 m=36 m,汽车运动距离为 18 m,二者最近距离为18 m+25 m-36 m=7 m,选项A、C错误,B正确.人不能追上公共汽车,且车开动后,人车距离先减小后增大,选项D错误.
答案:B
练6 解析:解法一:物理分析法
对B车,由运动学公式有0-v02=2ax,解得a=-0.25 m/s2,所以B车刹车的最大加速度为-0.25 m/s2,当B车速度减小到v=10 m/s时,两车相距最近,此时B车的位移为x1=v2-vB22a,A车的位移x2=vAt,t=v-vBa,联立解得x1=1 600 m,x2=800 m,能见度至少为Δx=x1-x2=800 m,选项C正确.
解法二:图象法
对B车,由运动学公式有0-v02=2ax,解得a=0-3022×1800 m/s2=-0.25 m/s2,作出A、B两车运动过程中的速度—时间图象如图所示,图线的交点的横坐标为两车速度相等的时刻,有t=vA-vBa=80 s,当两车速度相等时相距最近,此时两车不相撞,则以后不能相碰,由v ? t图象与坐标轴围成的面积表示位移可知,图象中阴影三角形的面积为能见度的最小值,则xmin=12×(30-10)×80 m=800 m,选项C正确.
答案:C
思维拓展
典例1 解析:根据v ? t图线与坐标轴围成的面积表示位移,可知游泳池长度L=1.25×20 m=25 m或者L=1.0×25 m=25 m,选项A正确;甲、乙的位移—时间图象如图所示,根据位移—时间图线的交点表示相遇可知,在0~60 s内甲、乙相遇3次,在0~120 s内甲、乙相遇5次,所以选项B、C正确;由甲、乙的位移—时间图象可知,甲、乙在t=100 s时在泳池的一端相遇,选项D错误.
答案:ABC
典例2 解析:(1)两车减速运动的加速度为:
a== m/s2=2.5 m/s2
甲车减速到v2所用时间为
t1== s=4 s
行驶过的距离为
x1=t1=×4 m=60 m
甲车从匀速运动到栏杆打开所用时间为
t2== s=2 s
甲车从减速到栏杆打开的总时间为
t甲=t1+t2=(4+2) s=6 s
乙车减速行驶到收费岛中心线的时间为
t3=v1a=202.5s=8 s
从减速到打开栏杆的总时间为
t乙=t0+t3=(15+8) s=23 s
人工收费通道和ETC通道打开栏杆放行的时间差
Δt=t乙-t甲=(23-6) s=17 s
(2)乙车从收费岛中心线开始出发又经t3=8 s加速到v1=72 km/h,与甲车达到共同速度,此时两车相距最远.这个过程乙车行驶的距离与之前乙车减速行驶的距离相等,x乙=x+d2=60+402m=80 m
从收费岛中心线开始,甲车先从v2=36 km/h加速至v1=72 km/h,这个时间为t1=4 s,然后匀速行驶,
x甲=x1+v1(t3+Δt-t1)=[60+20×(8+17-4)] m=480 m
故两车相距的最远距离为Δx=x甲-x乙=(480-80) m=400 m
答案:(1)17 s (2)400 m
练1 解析:甲车司机经t1=3 s的反应时间开始刹车,从司机发现无法变道时经t2=t1+v甲-v乙a=5.5 s两车速度相等(速度相等为临界条件),可画出甲车司机发现无法变道后两车运动的速度—时间图象如图所示,甲车比乙车多走的距离x=(v甲-v乙)t1+12 (v甲-v乙)(t2-t1)=53.125 m,两车相距最近的距离为s-x=100 m-53.125 m=46.875 m,约为47 m,选项C正确.
答案:C
练2 解析:(1)对甲车,速度由20 m/s减至6 m/s过程中的位移x1=v甲2-v022a甲=91 m
则甲车司机需在离收费站窗口至少x2=x0+x1=100 m处开始刹车.
(2)设甲刹车后经时间t,甲、乙两车速度相同,由运动学公式得v乙-a乙(t-t0)=v甲-a甲t,解得t=8 s
相同速度v=v甲-a甲t=4 m/s<6 m/s,所以乙车减速到v′=6 m/s时两车刚好不相撞为不相撞的临界条件(找准速度是关键)
乙车从34 m/s减速至6 m/s的过程中的位移为x3=v乙t0+v乙2-v'22a乙=157 m
所以在甲车司机开始刹车时,甲、乙的距离至少为x=x3-x1=66 m.
答案:(1)100 m (2)66 m
考点一 运动图象的理解
自主演练
1.直线运动的x ? t图象
(1)意义:反映了直线运动的物体位移随时间变化的规律.
(2)图线上某点切线的斜率的意义
①斜率大小:表示物体速度的大小.
②斜率的正负:表示物体速度的方向.
(3)两种特殊的x ? t图象.
①若x ? t图象是一条平行于时间轴的直线,说明物体处于静止状态.(如图甲所示).
②若x ? t的图象是一条倾斜的直线,说明物体在做匀速直线运动.(如图乙所示).
2.直线运动的v ? t图象
(1)意义:反映了直线运动的物体速度随时间变化的规律.
(2)图线上某点切线的斜率的意义
①斜率的大小:表示物体加速度的大小.
②斜率的正负:表示物体加速度的方向.
(3)两种特殊的v ? t图象
①匀速直线运动的v ? t图象是与横轴平行的直线.(如图甲所示)
②匀变速直线运动的v ? t图象是一条倾斜的直线.(如图乙所示)
(4)图线与坐标轴围成的“面积”的意义
①图线与坐标轴围成的“面积”表示相应时间的位移.
②若此面积在时间轴的上方,表示这段时间内的位移方向为正方向;若此面积在时间轴的下方,表示这段时间内的位移方向为负方向.
[多维练透]
1.A、B两物体沿同一直线运动,运动过程中的x ? t图象如图所示,下列说法正确的是( )
A.4 s时A物体运动方向发生改变
B.0~6 s内B物体的速度逐渐减小
C.0~5 s内两物体的平均速度相等
D.0~6 s内某时刻两物体的速度大小相等
2.下列所给的运动图象中能反映做直线运动的物体不会回到初始位置的是( )
3.下图甲为发射模型火箭的示意图,已知模型火箭质量m=1 kg,图乙为该段时间内火箭运动的v ? t图,关于火箭受力情况和运动情况,下列说法正确的是( )
A.火箭2 s时达到最高点
B.火箭在3 s时加速度的方向改变
C.火箭在1 s时和5 s时的加速度相同
D.火箭在4 s时位于发射点下方2 m处
考点二 运动图象的应用
师生共研
1.运用运动图象解题时的“六看”
x?t图象
v?t图象
纵截距
表示初位置
表示初速度
斜直线
表示匀速直线运动
表示匀变速直线运动
斜率
表示速度
表示加速度
面积
无实际意义
图线和时间轴围成的面积表示位移
交点
相遇点
速度相等点(临界条件点)
拐点
表示从一种运动变为另一种运动
表示从一种运动变为另一种运动
2.三点说明
(1)无论是x?t图象还是v?t图象都只能描述直线运动.
(2)x?t图象和v?t图象不表示物体运动的轨迹.
(3)x?t图象和v?t图象的形状由x与t、v与t的函数关系决定.
题型1 x?t图象的应用
例1 [2020·河北石家庄二中期末]甲、乙两车在同一条直线上行驶,它们运动的位移x随时间t变化的关系如图所示,已知乙车做匀变速直线运动,其图线与t轴相切于10 s处,则下列说法正确的是( )
A.甲车的初速度为零
B.乙车的初位置在x0=60 m处
C.乙车的加速度大小为1.6 m/s2
D.5 s时两车相遇,此时甲车速度较大
题型2 v?t图象的应用
例2 甲、乙两车在平直的公路上行驶,t=0时刻两车处于同一位置,其速度—时间图象如图所示,两图线交点处坐标及切线如图,则( )
A.t=8 s末,甲、乙两车相遇
B.t=2 s末,甲车的加速度大于乙车的加速度
C.在0~2 s内,甲车的位移小于乙车的位移
D.在2~8 s内,甲车的平均速度小于乙车的平均速度
[教你解决问题]―→读图析图
题型3 图象间的转换
解决图象转换类问题的一般流程:
例3 如图所示是一物体做直线运动的v ? t图象,则下列根据v ? t图象作出的加速度—时间(a ? t)图象和位移—时间(x ? t)图象正确的是( )
拓展点 其他运动图象
(1)a ? t图象:由v=v0+at可知图象与横轴所围成面积表示速度变化量Δv,如图甲所示.
(2) xt ? t图象:由x=v0t+12at2可得xt=v0+12at,图象的斜率为12a,如图乙所示.
(3)v2 ? x图象:由v2 ? v02=2ax可知v2=v02+2ax,图象斜率为2a.如图丙所示.
[2021·福建莆田模拟]如图所示为物体做直线运动的图象,下列说法正确的是( )
A.甲图中,物体在0~t0这段时间内的位移小于12v0t0
B.乙图中,物体的加速度为2 m/s2
C.丙图中,阴影面积表示t1~t2时间内物体的加速度变化量
D.丁图中,t=3 s时物体的速度为25 m/s
练1 [2021·湖北一模]如图所示,甲是某质点的位移—时间图象(抛物线),乙是另一质点的速度—时间图象,关于这两图象,下列说法中正确的是( )
A.由图甲可知,质点加速度为4 m/s2
B.由图甲可知,质点在前10 s内的平均速度大小为4 m/s
C.由图乙可知,质点在2~4 s内的位移为0
D.由图乙可知,质点在运动过程中,加速度的最大值为7.5 m/s2
练2 汽车甲和乙在同一公路上做直线运动,如图是它们运动过程中的v ? t图象,二者在t1和t2时刻的速度分别为v1和v2,则在t1到t2时间内( )
A.乙的加速度不断增大
B.甲与乙间距离越来越大
C.乙的平均速度v
练3 [2021·湖北荆门联考]A、B两小车在同一直线上运动,它们运动的位移s随时间t变化的关系如图所示,已知A车的s ? t图线为抛物线的一部分,图线的最高点在第7 s末,B车的s ? t图线为直线,则下列说法正确的是( )
A.A车的初速度为7 m/s
B.A车的加速度大小为2 m/s2
C.A车减速过程运动的位移大小为50 m
D.10 s末两车相遇时,B车的速度较大
题后反思
图象问题求解策略
考点三 追及和相遇问题
多维探究
题型1 |追及相遇问题常用的分析方法
1.分析技巧:可概括为“一个临界条件”“两个关系”.
2.能否追上的判断方法
物体B追赶物体A:开始时,两个物体相距x0,到vA=vB时,若xA+x0
3.特别提醒
若被追赶的物体做匀减速直线运动,一定要注意判断被追上前该物体是否已经停止运动.
例5 汽车A以vA=4 m/s的速度向右做匀速直线运动,汽车B以vB=10 m/s的速度同向运动,B在A前方x0=7 m处时汽车B开始匀减速刹车,直到静止后保持不动,B刹车的加速度大小a=2 m/s2,从汽车B开始刹车时计时.求:
(1)A追上B前,A、B间的最远距离是多少;
(2)经过多长时间A恰好追上B.
[教你解决问题]―→读题画过程示意图
题型2 与运动图象相结合的追及相遇问题
例6 [2021·武汉模拟]一辆汽车在平直的公路上匀速行驶,司机突然发现前方有一辆老年代步车正在慢速行驶,短暂反应后司机立即采取制动措施,结果汽车恰好没有撞上前方的老年代步车,若司机发现代步车时开始计时(t=0),两车的v ? t图象如图所示,则( )
A.图象中的a表示汽车,b表示老年代步车
B.汽车制动时的加速度大小为4.4 m/s2
C.从司机发现代步车到两车速度相等时经历的时间为3.0 s
D.司机发现代步车时汽车距离代步车30 m
练4 [2021·广州二调改编](多选)如图所示,图甲为质点a和b做直线运动的位移—时间(x ? t)图象,图乙为质点c和d做直线运动的速度—时间(v ? t)图象,由图可知( )
A.若t1时刻a、b两质点第一次相遇,则t2时刻两质点第二次相遇
B.若t1时刻c、d两质点第一次相遇,则t2时刻两质点第二次相遇
C.t1到t2时间内,b和d两个质点的运动方向发生了改变
D.t1到t2时间内,b和d两个质点的速度先减小后增大
练5 一步行者以6.0 m/s的速度跑去追赶被红灯阻停的公共汽车,在跑到距汽车25 m处时,绿灯亮了,汽车以1.0 m/s2的加速度匀加速启动前进,则( )
A.人能追上公共汽车,追赶过程中人跑了36 m
B.人不能追上公共汽车,人、车最近距离为7 m
C.人能追上公共汽车,追上车前人共跑了43 m
D.人不能追上公共汽车,且车开动后,人车距离越来越远
练6 A、B两辆列车在能见度很低的雾天里在同一轨道上同向行驶,A车在前,速度vA=10 m/s,B车在后,速度vB=30 m/s.当B车发现A车时就立刻刹车.已知B车在进行刹车测试时发现,若车以30 m/s的速度行驶时,刹车后至少要前进1 800 m才能停下,假设B车刹车过程中加速度恒定.为保证两辆列车不相撞,则能见度至少要达到( )
A.400 m B.600 m
C.800 m D.1 600 m
题后反思
追及相遇问题的解题流程
思维拓展
生活中多体多过程的运动学问题
题型1 体育+多体多过程问题
(多选)甲、乙两名运动员同时从泳池的两端出发,在泳池里训练,甲、乙的速度—时间图象分别如图(a)、(b)所示,不计转向的时间,两人的运动均可视为质点的直线运动.则( )
A.游泳池长25 m
B.经过1 min两人共相遇了3次
C.经过2 min两人共相遇了5次
D.两人一定不会在泳池的一端相遇
题型2 |交通+多体多过程问题
例2 为提高通行效率,许多高速公路出入口安装了电子不停车收费系统ETC.甲、乙两辆汽车分别通过ETC通道和人工收费通道(MTC)驶离高速公路,流程如图所示.假设减速带离收费岛口x=60 m,收费岛总长度d=40 m,两辆汽车同时以相同的速度v1=72 km/h经过减速带后,一起以相同的加速度做匀减速运动.甲车减速至v2=36 km/h后,匀速行驶到中心线即可完成缴费,自动栏杆打开放行;乙车刚好到收费岛中心线收费窗口停下,经过t0=15 s的时间缴费成功,人工栏杆打开放行.随后两辆汽车匀加速到速度v1后沿直线匀速行驶,设加速和减速过程中的加速度大小相等,求:
(1)此次人工收费通道和ETC通道打开栏杆放行的时间差;
(2)两辆汽车驶离收费站后相距的最远距离.
练1 [2021·湖北黄冈新起点考试]一辆从高速公路服务区驶出的小汽车甲以90 km/h的速度并入高速公路行车道向前行驶,甲车司机突然发现前方约100 m处有一辆正打开双闪的小汽车乙,以约45 km/h的速度缓慢行驶,此时甲车司机发现无法变道,经3 s的反应时间开始刹车,刹车加速度大小约为5 m/s2,则两车相距最近的距离约为( )
A.15 m B.53 m C.47 m D.63 m
练2 [2020·山东济南外国语学校5月月考]十一放假期间,全国高速公路对七座及以下小型客车免费放行,小轿车可以不停车通过收费站,但要求小轿车通过收费站窗口前x0=9 m区间的速度不超过v0=6 m/s.现在甲、乙两小轿车在收费站前平直公路上分别以v甲=20 m/s和v乙=34 m/s的速度匀速行驶,甲车在前,乙车在后.甲车司机发现正前方收费站,开始以大小为a甲=2 m/s2的加速度匀减速刹车.
(1)甲车司机需在离收费站窗口至少多远处开始刹车才不违章?
(2)若甲车司机经刹车到达离收费站窗口前9 m处的速度恰好为6 m/s,乙车司机在发现甲车刹车时经t0=0.5 s的反应时间后,开始以大小为a乙=4 m/s2的加速度匀减速刹车.为避免两车相撞,且乙车在收费站窗口前9 m区间不超速,则在甲车司机开始刹车时,甲、乙两车至少相距多远?
专题一 运动图象 追及相遇问题
考点突破
1.解析:A图线的斜率不变,则A物体的速度大小和方向不变,故A项错误;0~6 s内B物体图线切线的斜率增大,则B物体的速度逐渐增大,故B项错误;根据物体的位移Δx=x2-x1,可知0~5 s内,A物体的位移比B物体的大,则A物体的平均速度比B物体的大,故C项错误;0~6 s内B物体的图象切线斜率绝对值先小于A,后大于A,可知某时刻两物体的速度大小相等,故D项正确.
答案:D
2.解析:速度—时间图象中与坐标轴围成的面积表示位移,在坐标轴上方表示正位移,在坐标轴下方表示负位移,所以A项中面积不为零,位移不为零,物体不能回到初始位置;B、C两项中面积为零,位移为零,物体回到初始位置;位移—时间图象表示物体的位移随时间变化的图象,在t0时刻物体的位移为零,即物体又回到了初始位置.综上所述,A项正确.
答案:A
3.解析:2 s前后,运动方向不变,A项错误;3 s前后,v ? t图象的单调性不变,加速度方向不变,B项错误;由a=v-v0t得0~2 s内加速度a1=2 m/s2,4~6 s内加速度a2=2 m/s2,C项正确;0~3 s,v ? t图线所围面积x1=6 m,3~4 s,v ? t图线所围面积x2=-2 m,总位移为+4 m,表明火箭在4 s时位于发射点上方4 m处,D项错误.
答案:C
例1 解析:本题考查位移—时间图象.x ? t图线的斜率表示速度,则知甲车的速度不变,做匀速直线运动,初速度不为零,故A错误;甲车的速度v甲=ΔxΔt=205 m/s=4 m/s,乙车做匀变速直线运动,其图线与t轴相切于10 s处,则t=10 s时,乙车的速度为零,反过来看成乙车做初速度为零的匀加速直线运动,则有x=12at2,根据题图可知,20 m=12a·(5 s)2,解得乙车的加速度大小a=1.6 m/s2,则x0=80 m,故B错误,C正确;5 s时两车相遇,此时乙车的速度v乙=1.6×5 m/s=8 m/s,则乙车的速度较大,故D错误.
答案:C
例2 解析:根据速度—时间图线与坐标轴所围图形的面积表示位移可知,在0~8 s时间内,甲车的位移大于乙车的位移,又两车的初始位置相同,故t=8 s末,甲车在乙车前面,选项A错误;根据速度—时间图线的斜率表示加速度可知,在t=2 s时,甲车的加速度大小a1=5 m/s2,乙车的加速度大小a2=5 m/s2,甲、乙两车加速度大小相等,选项B错误;根据速度—时间图线与坐标轴所围图形的面积表示位移可知,在0~2 s时间内,甲车的位移小于乙车的位移,选项C正确;在2~8 s时间内,甲车的位移大于乙车的位移,根据平均速度公式可知,甲车的平均速度大于乙车的平均速度,选项D错误.
答案:C
例3 解析:由v ? t图象知,0~1 s内,物体做匀速直线运动,加速度a1=0,位移x=vt,x与t成正比;1~3 s内,物体的加速度不变,做匀变速直线运动,加速度a2=-1 m/s2,位移为x=v0(t-1 s)+12a2(t-1 s)2=-12t2+2t-32m,可知x ? t图象是开口向下的抛物线;3~5 s内,物体沿负方向做匀减速直线运动,加速度a3=0.5 m/s2,位移为x=-v0(t-3 s)+12a3(t-3 s)2,x ? t图象是开口向上的抛物线,且3~5 s内物体的位移为-1 m,由数学知识知,只有A选项对应的图象正确.
答案:A
例4 解析:由v ? t图线与坐标轴围成的面积表示位移,可知甲图中,物体在0~t0这段时间内的位移大于12v0t0(平均速度大于12v0),选项A错误;根据v2=2ax可知乙图中,2a=1 m/s2,则物体的加速度为0.5 m/s2,选项B错误;根据Δv=at可知,丙图中阴影部分的面积表示t1~t2时间内物体的速度变化量,选项C错误;由x=v0t+12at2可得xt=v0+12at,结合丁图可知12a=102 m/s2=5 m/s2(a前面的12易被忽视),即a=10 m/s2,则v0=-5 m/s,故t=3 s时物体的速度为v3=(-5+10×3) m/s=25 m/s,选项D正确.
答案:D
练1 解析:由图甲可知,x=12at2,取t=10 s,x=20 m,解得a=0.4 m/s2,质点在前10 s内的平均速度v=xt=2010 m/s=2 m/s,故A、B两项错误;由图乙可知,在2~4 s内,时间轴上方和下方的面积抵消,总位移为0,故C项正确;质点在运动过程中,加速度的最大值出现在2~4 s内,最大加速度大小为a=ΔvΔt=151 m/s2=15 m/s2,故D项错误.
答案:C
练2 解析:v ? t图象的斜率等于物体的加速度的大小,由图象知乙运动的加速度不断减小,t1时刻甲的加速度小于乙的加速度,选项A、D错误;由于不知道甲、乙初始位置关系,故无法判断二者间距离如何变化,选项B错误;乙在t1和t2时间内的位移小于做匀减速直线运动的位移,故平均速度v
练3 解析:本题考查匀变速直线运动与匀速直线运动的位移—时间图象的关系.A车做匀变速直线运动,设A车的初速度为v0,加速度大小为a,由题图可知,t=7 s时,速度为零,由运动学公式可得v7=v0-7a=0,根据图象和运动学公式可知,t′=10 s时的位移x10=40 m,x10=v0t′-12at′2=10v0-50a(m),联立解得a=2 m/s2,v0=14 m/s,故A错误,B正确;A车减速过程运动的位移大小x7=v0+02t=0+142×7 m=49 m,故C错误;位移—时间图线的斜率等于速度,10 s末两车相遇时B车的速度大小vB=ΔxΔt=4 m/s,A车的速度vA=v0-at′=-6 m/s,则A车的速度大于B车的速度,故D错误.
答案:B
例5 解析:(1)当A、B两汽车速度相等时,两车间的距离最远,此时有
v=vB-at=vA,解得t=3 s
此过程中汽车A的位移xA=vAt=12 m
汽车B的位移xB=vBt-12at2=21 m
故最远距离Δxmax=xB+x0-xA=16 m.
(2)汽车B从开始减速直到静止经历的时间t1=vBa=5 s
运动的位移x′B=vB22a=25 m
汽车A在t1时间内运动的位移x′A=vAt1=20 m
此时两车相距Δx=x′B+x0-x′A=12 m
汽车A需再运动的时间t2=ΔxvA=3 s
故A追上B所用时间t总=t1+t2=8 s.
答案:(1)16 m (2)8 s
例6 解析:汽车制动后速度减小,则知图象中的a表示老年代步车,b表示汽车,故A项错误;汽车制动时的加速度大小为a=ΔvΔt=204.5-0.5m/s2=5 m/s2,故B错误;设从汽车制动到两车速度相等时经历的时间为t,则va=vb-at,得t=va-vba=20-55 s=3 s,所以从司机发现代步车到两车速度相等时经历的时间为t′=t+0.5 s=3.5 s,故C项错误;汽车恰好没有撞上前方老年代步车的时刻是t=3.5 s,根据图线与坐标轴围成的面积表示位移大小,知司机发现代步车时汽车与代步车的距离s=0.5+3.52×15 m=30 m,故D项正确.
答案:D
练4 解析:位移—时间图象中两图线的交点表示两者相遇,根据图甲可知,选项A正确;速度—时间图象中两图线的交点表示两者速度相等,根据图乙可知,选项B错误;位移—时间图线斜率的正负表示运动方向,根据图甲可知,t1到t2时间内质点b的运动方向发生改变.速度—时间图线在t轴上方表示速度方向为正,根据图乙可知,t1到t2时间内质点d的运动方向不变,选项C错误;位移—时间图线的斜率表示速度,根据图甲可知,t1到t2时间内,质点b的速度先减小后增大.根据图乙可知,t1到t2时间内,质点d速度先减小后增大,选项D正确.
答案:AD
练5 解析:在跑到距汽车25 m处时,绿灯亮了,汽车以1.0 m/s2的加速度匀加速启动前进,当汽车加速到6.0 m/s时二者相距最近.汽车加速到6.0 m/s所用时间t=6 s,人运动距离为6×6 m=36 m,汽车运动距离为 18 m,二者最近距离为18 m+25 m-36 m=7 m,选项A、C错误,B正确.人不能追上公共汽车,且车开动后,人车距离先减小后增大,选项D错误.
答案:B
练6 解析:解法一:物理分析法
对B车,由运动学公式有0-v02=2ax,解得a=-0.25 m/s2,所以B车刹车的最大加速度为-0.25 m/s2,当B车速度减小到v=10 m/s时,两车相距最近,此时B车的位移为x1=v2-vB22a,A车的位移x2=vAt,t=v-vBa,联立解得x1=1 600 m,x2=800 m,能见度至少为Δx=x1-x2=800 m,选项C正确.
解法二:图象法
对B车,由运动学公式有0-v02=2ax,解得a=0-3022×1800 m/s2=-0.25 m/s2,作出A、B两车运动过程中的速度—时间图象如图所示,图线的交点的横坐标为两车速度相等的时刻,有t=vA-vBa=80 s,当两车速度相等时相距最近,此时两车不相撞,则以后不能相碰,由v ? t图象与坐标轴围成的面积表示位移可知,图象中阴影三角形的面积为能见度的最小值,则xmin=12×(30-10)×80 m=800 m,选项C正确.
答案:C
思维拓展
典例1 解析:根据v ? t图线与坐标轴围成的面积表示位移,可知游泳池长度L=1.25×20 m=25 m或者L=1.0×25 m=25 m,选项A正确;甲、乙的位移—时间图象如图所示,根据位移—时间图线的交点表示相遇可知,在0~60 s内甲、乙相遇3次,在0~120 s内甲、乙相遇5次,所以选项B、C正确;由甲、乙的位移—时间图象可知,甲、乙在t=100 s时在泳池的一端相遇,选项D错误.
答案:ABC
典例2 解析:(1)两车减速运动的加速度为:
a== m/s2=2.5 m/s2
甲车减速到v2所用时间为
t1== s=4 s
行驶过的距离为
x1=t1=×4 m=60 m
甲车从匀速运动到栏杆打开所用时间为
t2== s=2 s
甲车从减速到栏杆打开的总时间为
t甲=t1+t2=(4+2) s=6 s
乙车减速行驶到收费岛中心线的时间为
t3=v1a=202.5s=8 s
从减速到打开栏杆的总时间为
t乙=t0+t3=(15+8) s=23 s
人工收费通道和ETC通道打开栏杆放行的时间差
Δt=t乙-t甲=(23-6) s=17 s
(2)乙车从收费岛中心线开始出发又经t3=8 s加速到v1=72 km/h,与甲车达到共同速度,此时两车相距最远.这个过程乙车行驶的距离与之前乙车减速行驶的距离相等,x乙=x+d2=60+402m=80 m
从收费岛中心线开始,甲车先从v2=36 km/h加速至v1=72 km/h,这个时间为t1=4 s,然后匀速行驶,
x甲=x1+v1(t3+Δt-t1)=[60+20×(8+17-4)] m=480 m
故两车相距的最远距离为Δx=x甲-x乙=(480-80) m=400 m
答案:(1)17 s (2)400 m
练1 解析:甲车司机经t1=3 s的反应时间开始刹车,从司机发现无法变道时经t2=t1+v甲-v乙a=5.5 s两车速度相等(速度相等为临界条件),可画出甲车司机发现无法变道后两车运动的速度—时间图象如图所示,甲车比乙车多走的距离x=(v甲-v乙)t1+12 (v甲-v乙)(t2-t1)=53.125 m,两车相距最近的距离为s-x=100 m-53.125 m=46.875 m,约为47 m,选项C正确.
答案:C
练2 解析:(1)对甲车,速度由20 m/s减至6 m/s过程中的位移x1=v甲2-v022a甲=91 m
则甲车司机需在离收费站窗口至少x2=x0+x1=100 m处开始刹车.
(2)设甲刹车后经时间t,甲、乙两车速度相同,由运动学公式得v乙-a乙(t-t0)=v甲-a甲t,解得t=8 s
相同速度v=v甲-a甲t=4 m/s<6 m/s,所以乙车减速到v′=6 m/s时两车刚好不相撞为不相撞的临界条件(找准速度是关键)
乙车从34 m/s减速至6 m/s的过程中的位移为x3=v乙t0+v乙2-v'22a乙=157 m
所以在甲车司机开始刹车时,甲、乙的距离至少为x=x3-x1=66 m.
答案:(1)100 m (2)66 m
同课章节目录
