解直角三角形的应用(二）课件

(共14张PPT)
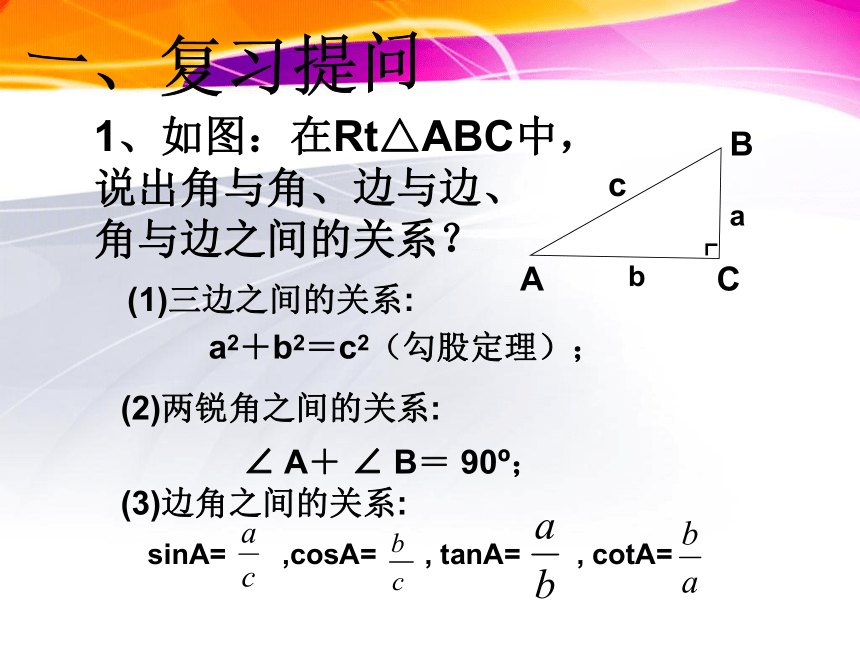
1、如图：在Rt△ABC中，
说出角与角、边与边、
角与边之间的关系？
A
C
B
a
b
c
┏
(1)三边之间的关系:
a2＋b2＝c2（勾股定理）；
(2)两锐角之间的关系:
∠ A＋ ∠ B＝ 90 ；
(3)边角之间的关系:
sinA= ,cosA= , tanA= , cotA=
2、解直角三角形的几种情况：
第一种：
已知一边和一锐角；
第二种：
已知两边
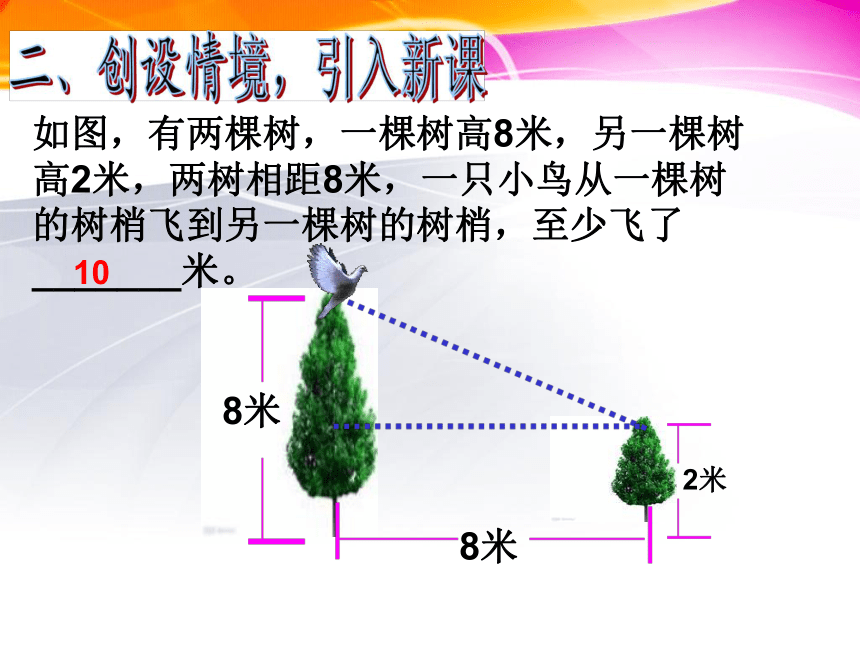
如图，有两棵树，一棵树高8米，另一棵树高2米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了_______米。
8米
8米
2米
10
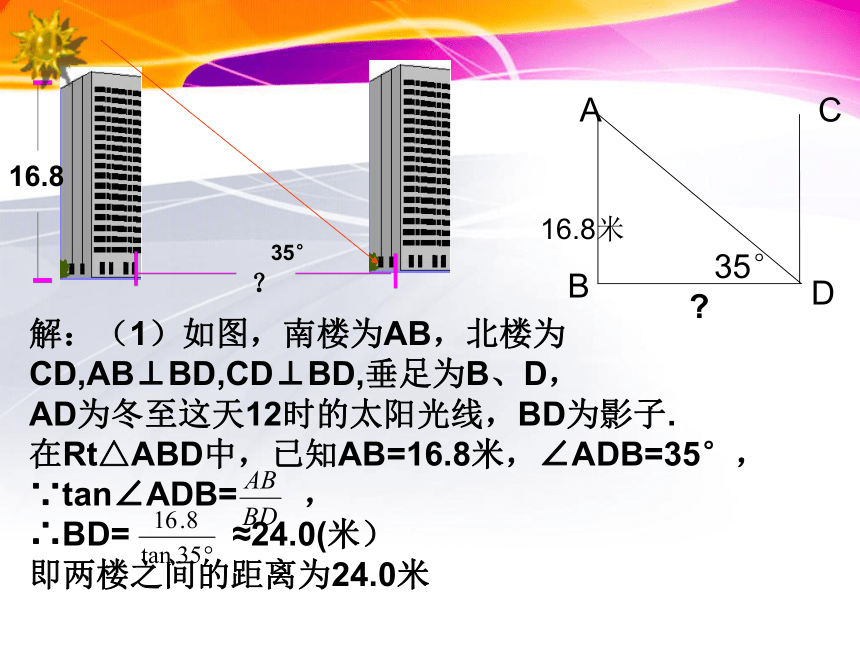
例1、住宅小区楼房之间的距离是建楼和购房
时人们所关心的问题之一。如图，住宅小区
南、北两栋楼房的高度均为16.8米。已知当
地冬至这天中午12时太阳光线与地面所成的
角是35°。
（1）要使这时南楼的影子恰好落在北楼的
墙角，两楼之间的距离应为多少米？（精确
到0.1米）
A
B
C
D
解：（1）如图，南楼为AB，北楼为
CD,AB⊥BD,CD⊥BD,垂足为B、D，
AD为冬至这天12时的太阳光线，BD为影子.
在Rt△ABD中，已知AB=16.8米，∠ADB=35°，
∵tan∠ADB= ，
∴BD= ≈24.0(米）
即两楼之间的距离为24.0米
16.8米
35°

16.8
？
35°
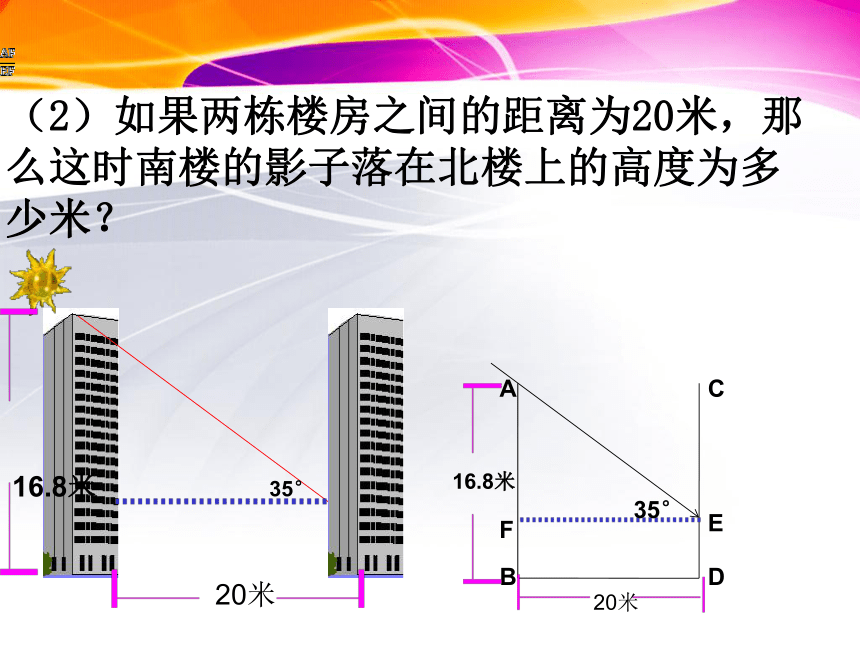
（2）如果两栋楼房之间的距离为20米，那么这时南楼的影子落在北楼上的高度为多少米？
16.8米
20米
35°
A
B
C
D
E
16.8米
20米
35°
F
解：（2）根据题意得，ED为AB落在CD上的影子。过点E作EF⊥AB于F, ∠AEF=35°，
EF=BD=20米,AB=16.8米，ED=FB
在Rt△AEF中，
∵tan∠AEF= ∴AF=EFtan∠AEF=20×tan35°≈14.0（米）∴ED=FB=16.8－14.0=2.8（米）
答：南楼在北楼上的影子是2.8米。
直角三角形边角之间的关系，是解决有关的实际问题
的重要切入点。把实际问题转化为直角三角形的问题，
关键是找出实际问题中的直角三角形，这一解答过程的
思路是：
有关实际问题 解直角三角形
问题答案 求出有关的边或角
--------
1、如图，一同学用测角仪在地点A测量旗杆BC的高度，
测角仪高AD=1m，地面上DC=20m,倾斜角α=30°，则
旗杆BC=____。
2、如图，平地上一棵树高为5米，两次观察地面上的影
子，第一次是阳光与地面成45°时，第二次是阳光与地
面成30°时，则第二次观察到的影子比第一次长____米。
A
B
D
C
30°
45°
A
B
C
D
E
30°
3、如图，两建筑物的水平距离为100米，从A点测得D点
的俯角是α，测得C点的俯角是β，则较低建筑物的高为__.
A
B
C
D
E
α
β
A
B
C
D
┓
4、如图，从地面上相距150米的A、B两点观察在C点的热气球出舱，分别测得仰角是30°和45°，试求C点距地面的距离。
5、如图，物化大厦离小为家60m，小伟从自家的窗中
眺望大厦，并测得大厦顶部的仰角为45°，而大厦底
部的俯角为30°。求该大厦的高度。
A
C
D
B
┏
有关实际问题 解直角三角形的问题
问题答案 求出有关的边或角
--------------