二次函数y=a(x-h)2+k的图像和性质
文档属性
| 名称 | 二次函数y=a(x-h)2+k的图像和性质 | 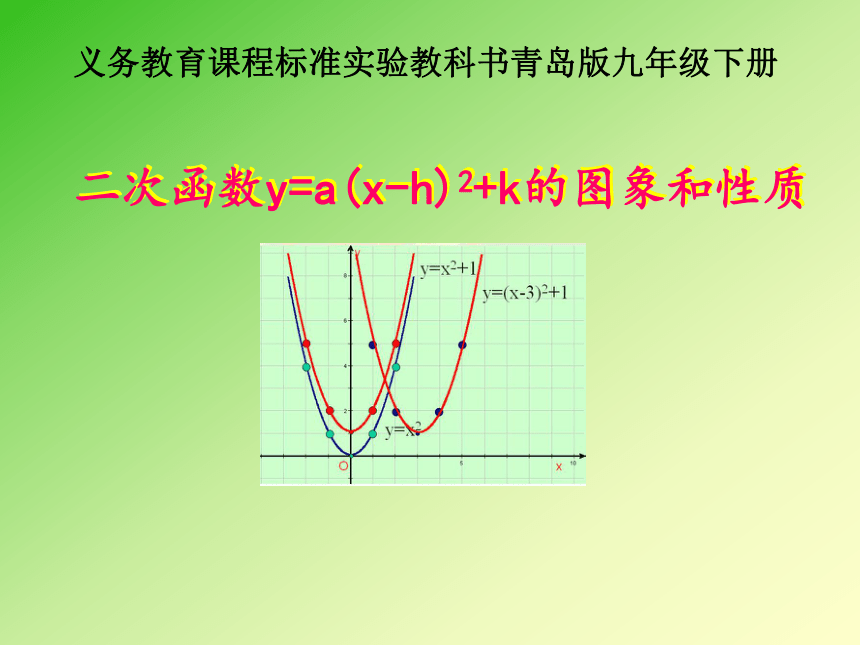 | |
| 格式 | zip | ||
| 文件大小 | 334.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-19 22:51:44 | ||
图片预览



文档简介
(共11张PPT)
二次函数y=a(x-h)2+k的图象和性质
二次函数y=a(x-h)2+k的图象和性质
义务教育课程标准实验教科书青岛版九年级下册
函数 开口方向 对称轴 顶 点坐 标 y的最值 增减性
在对称轴左侧 在对称轴右侧
y=ax2 a>0
a<0
y=ax2+k a>0
a<0
y=a(x-h)2 a>0
a<0
向上
Y轴
(0,0)
最小值是0
Y随x的增大而减小
Y随x的增大而增大
向下
Y轴
(0,0)
最大值是0
Y随x的增大而增大
Y随x的增大而减小
向上
Y轴
(0,k)
最小值是k
Y随x的增大而减小
Y随x的增大而增大
向下
Y轴
(0,k)
最大值是k
Y随x的增大而增大
Y随x的增大而减小
向上
直线x=h
(h,0)
Y随x的增大而减小
最小值是0
Y随x的增大而增大
向下
直线x=h
(h,0)
最大值是0
Y随x的增大而增大
Y随x的增大而减小
二次函数y=(x-3)2+1的图象是什么形状
是一条抛物线
在同一坐标系中作出二次函数y=x2和y=x2+1和y=(x-3)2+1的图象.
y=x2
y=x2+1
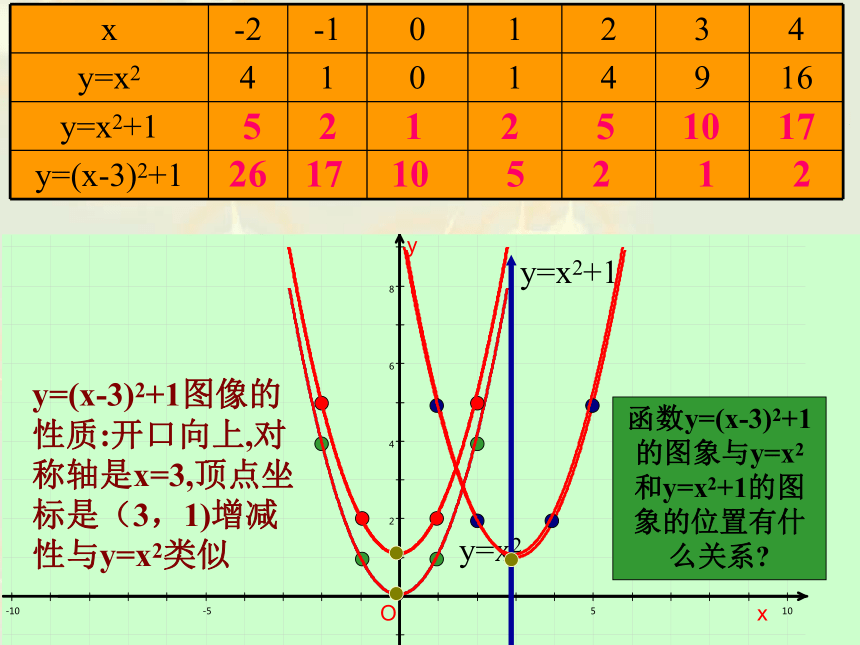
x -2 -1 0 1 2 3 4
y=x2 4 1 0 1 4 9 16
y=x2+1
y=(x-3)2+1
5 2 1 2 5 10 17
26 17 10 5 2 1 2
y=(x-3)2+1图像的性质:开口向上,对称轴是x=3,顶点坐标是(3,1)增减性与y=x2类似
函数y=(x-3)2+1的图象与y=x2和y=x2+1的图象的位置有什么关系
想一想,二次函数y=-3(x-1)2+2和y=-3x ,y=-3(x-1)2的图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么 .
.指出下列函数图象的开口方向对称轴和顶点坐标和极值:
1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.
2.填写下表:
y=a(x-h) +k 开口方向 对称轴 顶点坐标
a>0
a<0
二次函数y=a(x-h)2+k的图象和性质
1.顶点坐标与对称轴
. 2位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
例题分析:
一条抛物线的形状与抛物线
相同,其顶点坐标是(-1,3),写出这个抛物线的解析式.
解:设函数解析式为
又因为所求抛物线顶点坐标是(-1,3),所以h=-1,k=3
所以这个函数的解析式为:
即:
拓展:如果给我们的函数形式是:
因为所求抛物线的形状与
相同,所以a=-2.
图像如何画
相应练习:
一条抛物线的形状与抛物线
相同,其对称轴与抛物线
相同,且顶点的纵坐标是4,写出这条抛物
线的解析式.
作业:
1、课本35页练习。
2、练习册。
同学们,
再见!
二次函数y=a(x-h)2+k的图象和性质
二次函数y=a(x-h)2+k的图象和性质
义务教育课程标准实验教科书青岛版九年级下册
函数 开口方向 对称轴 顶 点坐 标 y的最值 增减性
在对称轴左侧 在对称轴右侧
y=ax2 a>0
a<0
y=ax2+k a>0
a<0
y=a(x-h)2 a>0
a<0
向上
Y轴
(0,0)
最小值是0
Y随x的增大而减小
Y随x的增大而增大
向下
Y轴
(0,0)
最大值是0
Y随x的增大而增大
Y随x的增大而减小
向上
Y轴
(0,k)
最小值是k
Y随x的增大而减小
Y随x的增大而增大
向下
Y轴
(0,k)
最大值是k
Y随x的增大而增大
Y随x的增大而减小
向上
直线x=h
(h,0)
Y随x的增大而减小
最小值是0
Y随x的增大而增大
向下
直线x=h
(h,0)
最大值是0
Y随x的增大而增大
Y随x的增大而减小
二次函数y=(x-3)2+1的图象是什么形状
是一条抛物线
在同一坐标系中作出二次函数y=x2和y=x2+1和y=(x-3)2+1的图象.
y=x2
y=x2+1
x -2 -1 0 1 2 3 4
y=x2 4 1 0 1 4 9 16
y=x2+1
y=(x-3)2+1
5 2 1 2 5 10 17
26 17 10 5 2 1 2
y=(x-3)2+1图像的性质:开口向上,对称轴是x=3,顶点坐标是(3,1)增减性与y=x2类似
函数y=(x-3)2+1的图象与y=x2和y=x2+1的图象的位置有什么关系
想一想,二次函数y=-3(x-1)2+2和y=-3x ,y=-3(x-1)2的图象有什么关系 它们的开口方向,对称轴和顶点坐标分别是什么 .
.指出下列函数图象的开口方向对称轴和顶点坐标和极值:
1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.
2.填写下表:
y=a(x-h) +k 开口方向 对称轴 顶点坐标
a>0
a<0
二次函数y=a(x-h)2+k的图象和性质
1.顶点坐标与对称轴
. 2位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
例题分析:
一条抛物线的形状与抛物线
相同,其顶点坐标是(-1,3),写出这个抛物线的解析式.
解:设函数解析式为
又因为所求抛物线顶点坐标是(-1,3),所以h=-1,k=3
所以这个函数的解析式为:
即:
拓展:如果给我们的函数形式是:
因为所求抛物线的形状与
相同,所以a=-2.
图像如何画
相应练习:
一条抛物线的形状与抛物线
相同,其对称轴与抛物线
相同,且顶点的纵坐标是4,写出这条抛物
线的解析式.
作业:
1、课本35页练习。
2、练习册。
同学们,
再见!
