人教B版(2019)必修第二册高中数学第四章指数函数、对数函数与幂函数章末复习 讲义
文档属性
| 名称 | 人教B版(2019)必修第二册高中数学第四章指数函数、对数函数与幂函数章末复习 讲义 |
|
|
| 格式 | zip | ||
| 文件大小 | 610.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 00:00:00 | ||
图片预览




文档简介
章末
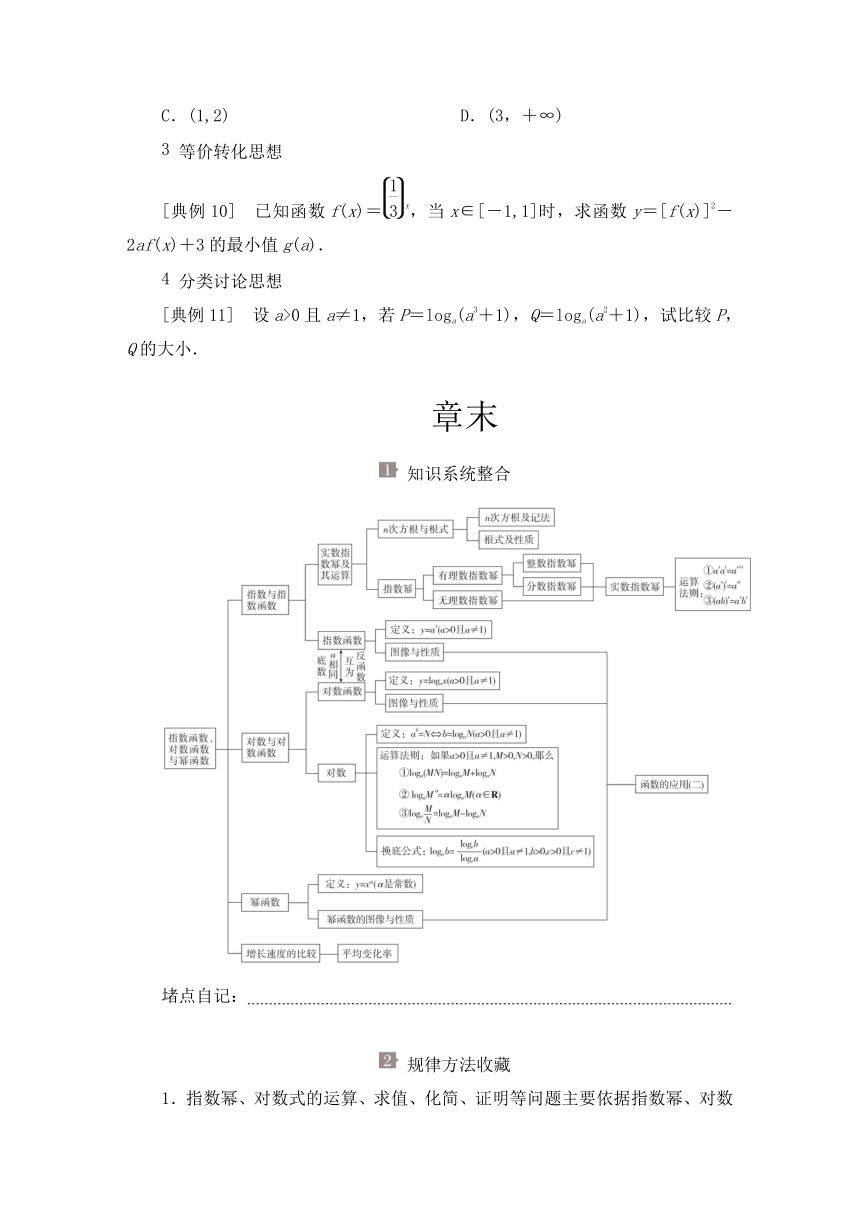
知识系统整合
堵点自记:
规律方法收藏
1.指数幂、对数式的运算、求值、化简、证明等问题主要依据指数幂、对数的运算性质,在进行指数、对数的运算时还要注意相互间的转化.
2.指数函数和对数函数的性质及图像特点是这部分知识的重点,而底数a的不同取值对函数的图像及性质的影响则是重中之重,要熟知a在(0,1)和(1,+∞)两个区间取值时函数的单调性及图像特点.
3.幂函数与指数函数的主要区别:幂函数的底数为变量,指数函数的指数为变量.因此,当遇到一个有关幂的形式的问题时,就要看变量所在的位置从而决定是用幂函数知识解决,还是用指数函数知识去解决.
4.比较几个数的大小是幂函数、指数函数、对数函数性质应用的常见题型,在具体比较时,可以首先将它们与零比较,分出正数、负数;再将正数与1比,分出大于1还是小于1;然后在各类中两两相比较.
5.求含有指数函数和对数函数的复合函数的最值或单调区间时,首先要考虑指数函数、对数函数的定义域,再由复合函数的单调性来确定其单调区间,要注意单调区间是函数定义域的子集.其次要结合函数的图像,观察确定其最值或单调区间.
6.函数图像是高考考查的重点内容,在历年高考中都有涉及.考查形式有知式选图、知图选式、图像变换以及用图像解题.函数图像形象地显示了函数的性质.在解方程或不等式时,特别是非常规的方程或不等式,画出图像,利用数形结合能起到十分快捷的效果.
7.在建立函数模型解决实际问题中,某些实际问题提供的变量关系是确定的,即设自变量为x,因变量为y,它们已建立了函数模型,我们可以利用该函数模型得出实际问题的答案.具体解题步骤为:
第一步,审题,引进数学符号,建立函数模型.了解变量的含义,若模型中含有待定系数,则需要进一步用待定系数法或其他方法确定.
第二步,求解函数模型.利用所学数学知识,如函数的单调性、最值等,对函数模型进行解答.
第三步,转译成实际问题的解.
学科思想培优
一、指数、对数、幂函数的典型问题及求解策略
指数函数、对数函数、幂函数的性质主要是指函数的定义域、值域、单调性等,其中单调性是高考考查的重点,并且经常以复合函数的形式考查,求解此类问题时,要以基本函数的单调性为主,结合复合函数单调性判断法则,在函数定义域内进行讨论.
求定义域
[典例1] (1)函数y=的定义域是( )
A.[-2,+∞)
B.[-1,+∞)
C.(-∞,-1]
D.(-∞,-2]
(2)函数f(x)=+的定义域为( )
A.[-2,0)∪(0,2]
B.(-1,0)∪(0,2]
C.[-2,2]
D.(-1,2]
比较大小问题
比较几个数的大小是指数、对数、幂函数的又一重要应用,其基本方法是:将两个需要比较大小的实数看成某类函数的函数值,然后利用该类函数的单调性进行比较;有时也采用搭桥法、图像法、特殊值法、作图法等.
[典例2] 若0A.3y<3x
B.logx3C.log4xD.x[典例3] 比较三个数0.32,log20.3,20.3的大小.
与指数、对数函数相关的单调性问题
[典例4] 是否存在实数a,使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数?如果存在,求出a的取值范围;如果不存在,请说明理由.
二、函数的图像问题
对于给定的函数图像,要能从函数左右、上下的分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性等性质.注意图像与函数解析式中参数的关系,能够通过变换画出函数的图像.
图像的变换
[典例5] 为了得到函数y=lg
的图像,只需把函数y=lg
x的图像上所有的点( )
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
根据图像比较底数或指数的大小
[典例6] 如图是幂函数y=xa,y=xb,y=xc,y=xd在第一象限内的图像,则a,b,c,d的大小关系为( )
A.aB.aC.bD.b根据函数解析式确定图像
[典例7] 已知f(x)=ax-2,g(x)=loga|x|(a>0,a≠1),若f(4)·g(-4)<0,则y=f(x),y=g(x)在同一平面直角坐标系内的大致图像是( )
三、数学思想方法
在解决与指数函数、对数函数、幂函数相关的问题中,常常用到多种思想方法.如比较大小、解不等式要对底数或其中的参数进行分类讨论;复合函数常常要转化成简单的二次函数、一次函数;方程不等式往往转化成函数来解决,同时利用函数图像,也体现了数形结合思想,等等.
函数与方程思想
[典例8] 若方程lg
(x-1)+lg
(3-x)=lg
(a-x)(a∈R)有解,求实数a的取值范围.
数形结合思想
[典例9] 方程log3x+x=3的解所在的区间为( )
A.(0,1)
B.(2,3)
C.(1,2)
D.(3,+∞)
等价转化思想
[典例10] 已知函数f(x)=x,当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a).
分类讨论思想
[典例11] 设a>0且a≠1,若P=loga(a3+1),Q=loga(a2+1),试比较P,Q的大小.
章末
知识系统整合
堵点自记:
规律方法收藏
1.指数幂、对数式的运算、求值、化简、证明等问题主要依据指数幂、对数的运算性质,在进行指数、对数的运算时还要注意相互间的转化.
2.指数函数和对数函数的性质及图像特点是这部分知识的重点,而底数a的不同取值对函数的图像及性质的影响则是重中之重,要熟知a在(0,1)和(1,+∞)两个区间取值时函数的单调性及图像特点.
3.幂函数与指数函数的主要区别:幂函数的底数为变量,指数函数的指数为变量.因此,当遇到一个有关幂的形式的问题时,就要看变量所在的位置从而决定是用幂函数知识解决,还是用指数函数知识去解决.
4.比较几个数的大小是幂函数、指数函数、对数函数性质应用的常见题型,在具体比较时,可以首先将它们与零比较,分出正数、负数;再将正数与1比,分出大于1还是小于1;然后在各类中两两相比较.
5.求含有指数函数和对数函数的复合函数的最值或单调区间时,首先要考虑指数函数、对数函数的定义域,再由复合函数的单调性来确定其单调区间,要注意单调区间是函数定义域的子集.其次要结合函数的图像,观察确定其最值或单调区间.
6.函数图像是高考考查的重点内容,在历年高考中都有涉及.考查形式有知式选图、知图选式、图像变换以及用图像解题.函数图像形象地显示了函数的性质.在解方程或不等式时,特别是非常规的方程或不等式,画出图像,利用数形结合能起到十分快捷的效果.
7.在建立函数模型解决实际问题中,某些实际问题提供的变量关系是确定的,即设自变量为x,因变量为y,它们已建立了函数模型,我们可以利用该函数模型得出实际问题的答案.具体解题步骤为:
第一步,审题,引进数学符号,建立函数模型.了解变量的含义,若模型中含有待定系数,则需要进一步用待定系数法或其他方法确定.
第二步,求解函数模型.利用所学数学知识,如函数的单调性、最值等,对函数模型进行解答.
第三步,转译成实际问题的解.
学科思想培优
一、指数、对数、幂函数的典型问题及求解策略
指数函数、对数函数、幂函数的性质主要是指函数的定义域、值域、单调性等,其中单调性是高考考查的重点,并且经常以复合函数的形式考查,求解此类问题时,要以基本函数的单调性为主,结合复合函数单调性判断法则,在函数定义域内进行讨论.
求定义域
[典例1] (1)函数y=的定义域是( )
A.[-2,+∞)
B.[-1,+∞)
C.(-∞,-1]
D.(-∞,-2]
(2)函数f(x)=+的定义域为( )
A.[-2,0)∪(0,2]
B.(-1,0)∪(0,2]
C.[-2,2]
D.(-1,2]
解析 (1)由题意得2x-1-27≥0,所以2x-1≥27,即2x-1≥-3,又指数函数y=x为R上的单调减函数,所以2x-1≤-3,解得x≤-1.
(2)要使函数有意义,需
即解得x∈(-1,0)∪(0,2].
答案 (1)C (2)B
比较大小问题
比较几个数的大小是指数、对数、幂函数的又一重要应用,其基本方法是:将两个需要比较大小的实数看成某类函数的函数值,然后利用该类函数的单调性进行比较;有时也采用搭桥法、图像法、特殊值法、作图法等.
[典例2] 若0A.3y<3x
B.logx3C.log4xD.x解析 因为0对于A,函数y=3x在R上单调递增,故3x<3y,错误.
对于B,根据底数a对对数函数y=logax的影响:当0logy3,错误.
对于C,函数y=log4x在(0,+∞)上单调递增,故log4x对于D,函数y=x在R上单调递减,故x>y,错误.
答案 C
[典例3] 比较三个数0.32,log20.3,20.3的大小.
解 解法一:∵0<0.32<12=1,log20.320=1,∴log20.3<0.32<20.3.
解法二:作出函数y=x2,y=log2x,y=2x的大致图像,如图所示,画出直线x=0.3,根据直线与三个函数图像的交点位置,即可看出log20.3<0.32<20.3.
与指数、对数函数相关的单调性问题
[典例4] 是否存在实数a,使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数?如果存在,求出a的取值范围;如果不存在,请说明理由.
解 设g(x)=ax2-x,假设符合条件的a存在.
当a>1时,为使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数,只需g(x)=ax2-x在区间[2,4]上是增函数,故应满足解得a>,∴a>1.
当0综上可知,当a>1时,f(x)=loga(ax2-x)在区间[2,4]上为增函数.
二、函数的图像问题
对于给定的函数图像,要能从函数左右、上下的分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性等性质.注意图像与函数解析式中参数的关系,能够通过变换画出函数的图像.
图像的变换
[典例5] 为了得到函数y=lg
的图像,只需把函数y=lg
x的图像上所有的点( )
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
解析 ∵y=lg
=lg
(x+3)-1,∴只需将函数y=lg
x
的图像上所有的点向左平移3个单位长度,再向下平移1个单位长度,即可得到函数y=lg
的图像.
答案 C
根据图像比较底数或指数的大小
[典例6] 如图是幂函数y=xa,y=xb,y=xc,y=xd在第一象限内的图像,则a,b,c,d的大小关系为( )
A.aB.aC.bD.b解析 作直线x=2,如图所示,直线与4个幂函数图像交点的纵坐标分别为2a,2b,2c,2d.由图可知2a<2b<2c<2d,而函数y=2x为增函数,所以a答案 A
根据函数解析式确定图像
[典例7] 已知f(x)=ax-2,g(x)=loga|x|(a>0,a≠1),若f(4)·g(-4)<0,则y=f(x),y=g(x)在同一平面直角坐标系内的大致图像是( )
解析 由f(4)·g(-4)<0知a2·loga4<0,∴loga4<0,∴0答案 B
三、数学思想方法
在解决与指数函数、对数函数、幂函数相关的问题中,常常用到多种思想方法.如比较大小、解不等式要对底数或其中的参数进行分类讨论;复合函数常常要转化成简单的二次函数、一次函数;方程不等式往往转化成函数来解决,同时利用函数图像,也体现了数形结合思想,等等.
函数与方程思想
[典例8] 若方程lg
(x-1)+lg
(3-x)=lg
(a-x)(a∈R)有解,求实数a的取值范围.
解 原方程等价于
即
设函数f(x)=-x2+5x-3,因为1数形结合思想
[典例9] 方程log3x+x=3的解所在的区间为( )
A.(0,1)
B.(2,3)
C.(1,2)
D.(3,+∞)
解析 ∵方程log3x+x=3可变形为log3x=3-x,而方程log3x=3-x的解,就是函数y=log3x和函数y=3-x的交点的横坐标,根据两个函数的图像可知两个函数图像的交点的横坐标一定在区间(1,3)内.
因函数f(x)=log3x+x-3在区间(1,2)上不满足f(1)·f(2)<0,所以方程log3x+x=3的解所在的区间是(2,3).故选B.
答案 B
等价转化思想
[典例10] 已知函数f(x)=x,当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a).
解 ∵x∈[-1,1],∴x∈.
∴y=[f(x)]2-2af(x)+3=2x-2ax+3
=2+3-a2.
令t=x,则t∈.
若a<,则当t=,
即x=1时,ymin=-+3=-.
若≤a≤3,则当t=a,即x=loga时,ymin=3-a2.
若a>3,则当t=3,即x=-1时,
ymin=9-6a+3=12-6a.
综上可知,g(a)=
分类讨论思想
[典例11] 设a>0且a≠1,若P=loga(a3+1),Q=loga(a2+1),试比较P,Q的大小.
解 当0又当0∴loga(a3+1)>loga(a2+1),即P>Q.
当a>1时,有a3>a2,即a3+1>a2+1.
又当a>1时,y=logax在(0,+∞)上单调递增,
∴loga(a3+1)>loga(a2+1),即P>Q.
综上可得,P>Q.
知识系统整合
堵点自记:
规律方法收藏
1.指数幂、对数式的运算、求值、化简、证明等问题主要依据指数幂、对数的运算性质,在进行指数、对数的运算时还要注意相互间的转化.
2.指数函数和对数函数的性质及图像特点是这部分知识的重点,而底数a的不同取值对函数的图像及性质的影响则是重中之重,要熟知a在(0,1)和(1,+∞)两个区间取值时函数的单调性及图像特点.
3.幂函数与指数函数的主要区别:幂函数的底数为变量,指数函数的指数为变量.因此,当遇到一个有关幂的形式的问题时,就要看变量所在的位置从而决定是用幂函数知识解决,还是用指数函数知识去解决.
4.比较几个数的大小是幂函数、指数函数、对数函数性质应用的常见题型,在具体比较时,可以首先将它们与零比较,分出正数、负数;再将正数与1比,分出大于1还是小于1;然后在各类中两两相比较.
5.求含有指数函数和对数函数的复合函数的最值或单调区间时,首先要考虑指数函数、对数函数的定义域,再由复合函数的单调性来确定其单调区间,要注意单调区间是函数定义域的子集.其次要结合函数的图像,观察确定其最值或单调区间.
6.函数图像是高考考查的重点内容,在历年高考中都有涉及.考查形式有知式选图、知图选式、图像变换以及用图像解题.函数图像形象地显示了函数的性质.在解方程或不等式时,特别是非常规的方程或不等式,画出图像,利用数形结合能起到十分快捷的效果.
7.在建立函数模型解决实际问题中,某些实际问题提供的变量关系是确定的,即设自变量为x,因变量为y,它们已建立了函数模型,我们可以利用该函数模型得出实际问题的答案.具体解题步骤为:
第一步,审题,引进数学符号,建立函数模型.了解变量的含义,若模型中含有待定系数,则需要进一步用待定系数法或其他方法确定.
第二步,求解函数模型.利用所学数学知识,如函数的单调性、最值等,对函数模型进行解答.
第三步,转译成实际问题的解.
学科思想培优
一、指数、对数、幂函数的典型问题及求解策略
指数函数、对数函数、幂函数的性质主要是指函数的定义域、值域、单调性等,其中单调性是高考考查的重点,并且经常以复合函数的形式考查,求解此类问题时,要以基本函数的单调性为主,结合复合函数单调性判断法则,在函数定义域内进行讨论.
求定义域
[典例1] (1)函数y=的定义域是( )
A.[-2,+∞)
B.[-1,+∞)
C.(-∞,-1]
D.(-∞,-2]
(2)函数f(x)=+的定义域为( )
A.[-2,0)∪(0,2]
B.(-1,0)∪(0,2]
C.[-2,2]
D.(-1,2]
比较大小问题
比较几个数的大小是指数、对数、幂函数的又一重要应用,其基本方法是:将两个需要比较大小的实数看成某类函数的函数值,然后利用该类函数的单调性进行比较;有时也采用搭桥法、图像法、特殊值法、作图法等.
[典例2] 若0
B.logx3
与指数、对数函数相关的单调性问题
[典例4] 是否存在实数a,使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数?如果存在,求出a的取值范围;如果不存在,请说明理由.
二、函数的图像问题
对于给定的函数图像,要能从函数左右、上下的分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性等性质.注意图像与函数解析式中参数的关系,能够通过变换画出函数的图像.
图像的变换
[典例5] 为了得到函数y=lg
的图像,只需把函数y=lg
x的图像上所有的点( )
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
根据图像比较底数或指数的大小
[典例6] 如图是幂函数y=xa,y=xb,y=xc,y=xd在第一象限内的图像,则a,b,c,d的大小关系为( )
A.a
[典例7] 已知f(x)=ax-2,g(x)=loga|x|(a>0,a≠1),若f(4)·g(-4)<0,则y=f(x),y=g(x)在同一平面直角坐标系内的大致图像是( )
三、数学思想方法
在解决与指数函数、对数函数、幂函数相关的问题中,常常用到多种思想方法.如比较大小、解不等式要对底数或其中的参数进行分类讨论;复合函数常常要转化成简单的二次函数、一次函数;方程不等式往往转化成函数来解决,同时利用函数图像,也体现了数形结合思想,等等.
函数与方程思想
[典例8] 若方程lg
(x-1)+lg
(3-x)=lg
(a-x)(a∈R)有解,求实数a的取值范围.
数形结合思想
[典例9] 方程log3x+x=3的解所在的区间为( )
A.(0,1)
B.(2,3)
C.(1,2)
D.(3,+∞)
等价转化思想
[典例10] 已知函数f(x)=x,当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a).
分类讨论思想
[典例11] 设a>0且a≠1,若P=loga(a3+1),Q=loga(a2+1),试比较P,Q的大小.
章末
知识系统整合
堵点自记:
规律方法收藏
1.指数幂、对数式的运算、求值、化简、证明等问题主要依据指数幂、对数的运算性质,在进行指数、对数的运算时还要注意相互间的转化.
2.指数函数和对数函数的性质及图像特点是这部分知识的重点,而底数a的不同取值对函数的图像及性质的影响则是重中之重,要熟知a在(0,1)和(1,+∞)两个区间取值时函数的单调性及图像特点.
3.幂函数与指数函数的主要区别:幂函数的底数为变量,指数函数的指数为变量.因此,当遇到一个有关幂的形式的问题时,就要看变量所在的位置从而决定是用幂函数知识解决,还是用指数函数知识去解决.
4.比较几个数的大小是幂函数、指数函数、对数函数性质应用的常见题型,在具体比较时,可以首先将它们与零比较,分出正数、负数;再将正数与1比,分出大于1还是小于1;然后在各类中两两相比较.
5.求含有指数函数和对数函数的复合函数的最值或单调区间时,首先要考虑指数函数、对数函数的定义域,再由复合函数的单调性来确定其单调区间,要注意单调区间是函数定义域的子集.其次要结合函数的图像,观察确定其最值或单调区间.
6.函数图像是高考考查的重点内容,在历年高考中都有涉及.考查形式有知式选图、知图选式、图像变换以及用图像解题.函数图像形象地显示了函数的性质.在解方程或不等式时,特别是非常规的方程或不等式,画出图像,利用数形结合能起到十分快捷的效果.
7.在建立函数模型解决实际问题中,某些实际问题提供的变量关系是确定的,即设自变量为x,因变量为y,它们已建立了函数模型,我们可以利用该函数模型得出实际问题的答案.具体解题步骤为:
第一步,审题,引进数学符号,建立函数模型.了解变量的含义,若模型中含有待定系数,则需要进一步用待定系数法或其他方法确定.
第二步,求解函数模型.利用所学数学知识,如函数的单调性、最值等,对函数模型进行解答.
第三步,转译成实际问题的解.
学科思想培优
一、指数、对数、幂函数的典型问题及求解策略
指数函数、对数函数、幂函数的性质主要是指函数的定义域、值域、单调性等,其中单调性是高考考查的重点,并且经常以复合函数的形式考查,求解此类问题时,要以基本函数的单调性为主,结合复合函数单调性判断法则,在函数定义域内进行讨论.
求定义域
[典例1] (1)函数y=的定义域是( )
A.[-2,+∞)
B.[-1,+∞)
C.(-∞,-1]
D.(-∞,-2]
(2)函数f(x)=+的定义域为( )
A.[-2,0)∪(0,2]
B.(-1,0)∪(0,2]
C.[-2,2]
D.(-1,2]
解析 (1)由题意得2x-1-27≥0,所以2x-1≥27,即2x-1≥-3,又指数函数y=x为R上的单调减函数,所以2x-1≤-3,解得x≤-1.
(2)要使函数有意义,需
即解得x∈(-1,0)∪(0,2].
答案 (1)C (2)B
比较大小问题
比较几个数的大小是指数、对数、幂函数的又一重要应用,其基本方法是:将两个需要比较大小的实数看成某类函数的函数值,然后利用该类函数的单调性进行比较;有时也采用搭桥法、图像法、特殊值法、作图法等.
[典例2] 若0
B.logx3
对于B,根据底数a对对数函数y=logax的影响:当0
对于C,函数y=log4x在(0,+∞)上单调递增,故log4x
答案 C
[典例3] 比较三个数0.32,log20.3,20.3的大小.
解 解法一:∵0<0.32<12=1,log20.3
解法二:作出函数y=x2,y=log2x,y=2x的大致图像,如图所示,画出直线x=0.3,根据直线与三个函数图像的交点位置,即可看出log20.3<0.32<20.3.
与指数、对数函数相关的单调性问题
[典例4] 是否存在实数a,使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数?如果存在,求出a的取值范围;如果不存在,请说明理由.
解 设g(x)=ax2-x,假设符合条件的a存在.
当a>1时,为使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数,只需g(x)=ax2-x在区间[2,4]上是增函数,故应满足解得a>,∴a>1.
当0
二、函数的图像问题
对于给定的函数图像,要能从函数左右、上下的分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性等性质.注意图像与函数解析式中参数的关系,能够通过变换画出函数的图像.
图像的变换
[典例5] 为了得到函数y=lg
的图像,只需把函数y=lg
x的图像上所有的点( )
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
解析 ∵y=lg
=lg
(x+3)-1,∴只需将函数y=lg
x
的图像上所有的点向左平移3个单位长度,再向下平移1个单位长度,即可得到函数y=lg
的图像.
答案 C
根据图像比较底数或指数的大小
[典例6] 如图是幂函数y=xa,y=xb,y=xc,y=xd在第一象限内的图像,则a,b,c,d的大小关系为( )
A.a
根据函数解析式确定图像
[典例7] 已知f(x)=ax-2,g(x)=loga|x|(a>0,a≠1),若f(4)·g(-4)<0,则y=f(x),y=g(x)在同一平面直角坐标系内的大致图像是( )
解析 由f(4)·g(-4)<0知a2·loga4<0,∴loga4<0,∴0
三、数学思想方法
在解决与指数函数、对数函数、幂函数相关的问题中,常常用到多种思想方法.如比较大小、解不等式要对底数或其中的参数进行分类讨论;复合函数常常要转化成简单的二次函数、一次函数;方程不等式往往转化成函数来解决,同时利用函数图像,也体现了数形结合思想,等等.
函数与方程思想
[典例8] 若方程lg
(x-1)+lg
(3-x)=lg
(a-x)(a∈R)有解,求实数a的取值范围.
解 原方程等价于
即
设函数f(x)=-x2+5x-3,因为1
[典例9] 方程log3x+x=3的解所在的区间为( )
A.(0,1)
B.(2,3)
C.(1,2)
D.(3,+∞)
解析 ∵方程log3x+x=3可变形为log3x=3-x,而方程log3x=3-x的解,就是函数y=log3x和函数y=3-x的交点的横坐标,根据两个函数的图像可知两个函数图像的交点的横坐标一定在区间(1,3)内.
因函数f(x)=log3x+x-3在区间(1,2)上不满足f(1)·f(2)<0,所以方程log3x+x=3的解所在的区间是(2,3).故选B.
答案 B
等价转化思想
[典例10] 已知函数f(x)=x,当x∈[-1,1]时,求函数y=[f(x)]2-2af(x)+3的最小值g(a).
解 ∵x∈[-1,1],∴x∈.
∴y=[f(x)]2-2af(x)+3=2x-2ax+3
=2+3-a2.
令t=x,则t∈.
若a<,则当t=,
即x=1时,ymin=-+3=-.
若≤a≤3,则当t=a,即x=loga时,ymin=3-a2.
若a>3,则当t=3,即x=-1时,
ymin=9-6a+3=12-6a.
综上可知,g(a)=
分类讨论思想
[典例11] 设a>0且a≠1,若P=loga(a3+1),Q=loga(a2+1),试比较P,Q的大小.
解 当0
当a>1时,有a3>a2,即a3+1>a2+1.
又当a>1时,y=logax在(0,+∞)上单调递增,
∴loga(a3+1)>loga(a2+1),即P>Q.
综上可得,P>Q.
