北师大版九年级数学下册:3.7《切线长定理》教案
文档属性
| 名称 | 北师大版九年级数学下册:3.7《切线长定理》教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 440.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 00:00:00 | ||
图片预览

文档简介
《切线长定理》教案
一、教学目标
1.知识技能
切线长定理及其证明、运用
2.过程与方法:经历探索切线长定理的过程,体验由特殊到一般的探索过程.
3.情感态度与价值观:
通过引言的教学,激发学生的学习兴趣,培养学生的知识来源于实践又反过来作用于实践的辩证唯物物主义观念.
学习重点:切线长定理
学习难点:切线长定理的探索及运用.
二、教学过程
1.问题情景引入
1)如何过⊙O外一点P画出⊙O的切线?
2)这样的切线能画出几条?
2.学生活动:做一做:如何用圆规和直尺作出这两条切线呢?
思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,连接OP,A,B 除了在⊙O上,还在怎样的圆上?
3.议一议:如图 3-30,PA,PB 是 ⊙O 的两条切线,A,B 是切点.
1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
2)在这个图中你能发现相等的线段吗?说说你的理由
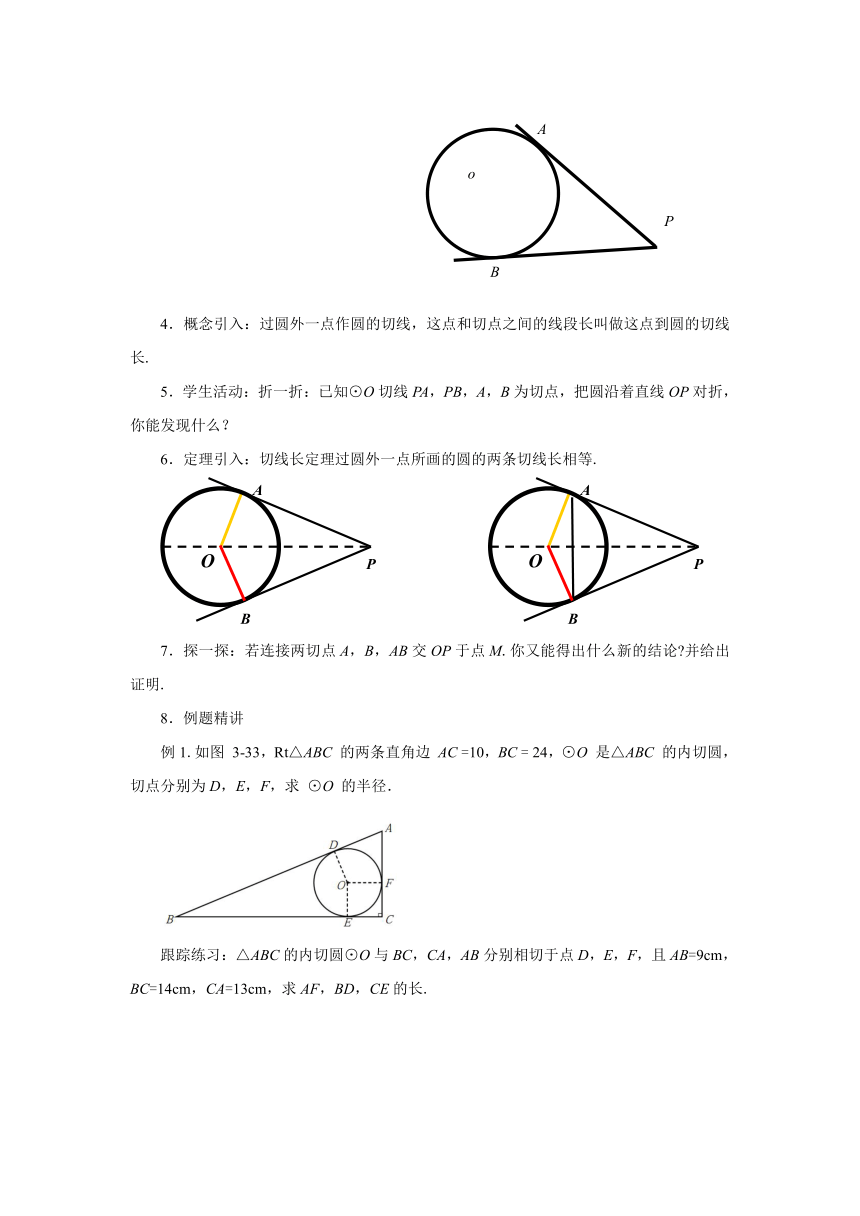
4.概念引入:过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
5.学生活动:折一折:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么?
6.定理引入:切线长定理过圆外一点所画的圆的两条切线长相等.
7.探一探:若连接两切点A,B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
8.例题精讲
例1.如图 3-33,Rt△ABC 的两条直角边 AC =10,BC = 24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求 ⊙O 的半径.
跟踪练习:△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
9.合作探究:如图 ,四边形ABCD的四条边都与 ⊙O 相切,图中的线段之间有哪些等量关系?与同伴进行交流.
10.课堂检测:
1)如图,PA,PB是⊙ O的切线,切点分别是A,B,如果∠P=60°,那么∠PAB等于( )
A.60° B.90° C.120° D.150°
2) PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于点C.如果PA=4cm,PD=2cm,求半径OA的长.
3)设△ABC的边BC=8,AC=11,AB=15,内切圆⊙I和BC,AC,AB分别相切于点D,E,F.
求AE,CD,BF的长.
4)已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=5cm,求△PEF的周长.
三、课堂小结:
四、课后反思:
一、教学目标
1.知识技能
切线长定理及其证明、运用
2.过程与方法:经历探索切线长定理的过程,体验由特殊到一般的探索过程.
3.情感态度与价值观:
通过引言的教学,激发学生的学习兴趣,培养学生的知识来源于实践又反过来作用于实践的辩证唯物物主义观念.
学习重点:切线长定理
学习难点:切线长定理的探索及运用.
二、教学过程
1.问题情景引入
1)如何过⊙O外一点P画出⊙O的切线?
2)这样的切线能画出几条?
2.学生活动:做一做:如何用圆规和直尺作出这两条切线呢?
思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,连接OP,A,B 除了在⊙O上,还在怎样的圆上?
3.议一议:如图 3-30,PA,PB 是 ⊙O 的两条切线,A,B 是切点.
1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
2)在这个图中你能发现相等的线段吗?说说你的理由
4.概念引入:过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
5.学生活动:折一折:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么?
6.定理引入:切线长定理过圆外一点所画的圆的两条切线长相等.
7.探一探:若连接两切点A,B,AB交OP于点M.你又能得出什么新的结论?并给出证明.
8.例题精讲
例1.如图 3-33,Rt△ABC 的两条直角边 AC =10,BC = 24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求 ⊙O 的半径.
跟踪练习:△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
9.合作探究:如图 ,四边形ABCD的四条边都与 ⊙O 相切,图中的线段之间有哪些等量关系?与同伴进行交流.
10.课堂检测:
1)如图,PA,PB是⊙ O的切线,切点分别是A,B,如果∠P=60°,那么∠PAB等于( )
A.60° B.90° C.120° D.150°
2) PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于点C.如果PA=4cm,PD=2cm,求半径OA的长.
3)设△ABC的边BC=8,AC=11,AB=15,内切圆⊙I和BC,AC,AB分别相切于点D,E,F.
求AE,CD,BF的长.
4)已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=5cm,求△PEF的周长.
三、课堂小结:
四、课后反思:
