北师大版九年级数学下册:3.3垂径定理 教案
文档属性
| 名称 | 北师大版九年级数学下册:3.3垂径定理 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 392.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-14 15:00:45 | ||
图片预览

文档简介
课题 3.3垂径定理 课型 新课
课时 第一课时 教学方法 小组合作,探索交流
教材 北师大版九年级数学下册第三章圆
教学目标 1知识技能目标:
? 理解垂径定理和推论的内容,并会证明,掌握弦、弧、直径之间的特定关系,并会利用垂径定理解决与圆有关问题。
2过程方法目标:
? 经历探索垂径定理和推论的证明过程,掌握从特殊到一般,由猜测到论证的证明思路。
学会与人合作探索获得新知识的一些方法。
3情感态度与价值观:
? 通过参与垂径定理的数学活动,体会垂径定理的重要性,品尝成功的经验,体验数学活动充满着探索和创造。
教学重点 1 垂径定理以及推论的证明,
2 垂径定理的简单应用,
教学难点 ? ?垂径定理及其推论的正确区分及运用
教学方法 讨论法、探索法
教学用具 ? ? 多媒体 ,? 投影仪
教? 学? 过? 程
教学环节 教师活动 学生活动 教学意图
(一) 创设情境
引入新知
? 一、动脑想一想(出示幻灯片)
1请欣赏下列图片,并思考这些美丽的图案有什么共同特征?
?
2我们学过图形中轴对称图形有哪些?
? 它们各有几条对称轴呢?
3圆是不是轴对称图形呢?我们今天就来研究它。
? 学生通过观察,指出他们都是轴对称图形,并指出对称轴。
?学生答:线段、等腰三角形,等边三角形,矩形,菱形,正方形,等腰梯形,圆。
?
学生通过折纸活动,很容易答出:圆是轴对称图形。它有无数条对称轴,对称轴是-----?
学生答案1:它的直径。、
学生答案2:经过圆心的直线 由图片引出轴对称的知识,并将其引入圆中来,可以使学生更深刻的体会生活中处处蕴含着数学.
回顾学过的几何图形的对称性,为下面学习圆的对称性做铺垫,
通过折纸活动,训练和提高学生的动手实践能力以及空间想象能力,为解决折叠问题提供思路,
?
强化对称轴是一条直线的概念。训练学生使用准确的数学语言描述问题。
(二) 动手实践,合作探索 二、动手折一折
? ? 请同学们拿出事先准备好的圆形纸片,按老师的要求来做。
在圆形纸片上任意画一条直径,然后把这个圆形纸片沿着这条直径对折,观察折叠后的两个半圆有何关系?最后得出什么结论?(填空)
??结论 1圆是? 轴 ?对称图形,
2它有? 无数? 条对称轴,
3 经过圆心的每一条直线? 都是它的对称轴。
请同学们讨论一下如何描述圆的对称轴。
圆是轴对称图形,它还有哪些性质呢?
(三) 知识延伸
思维拓展
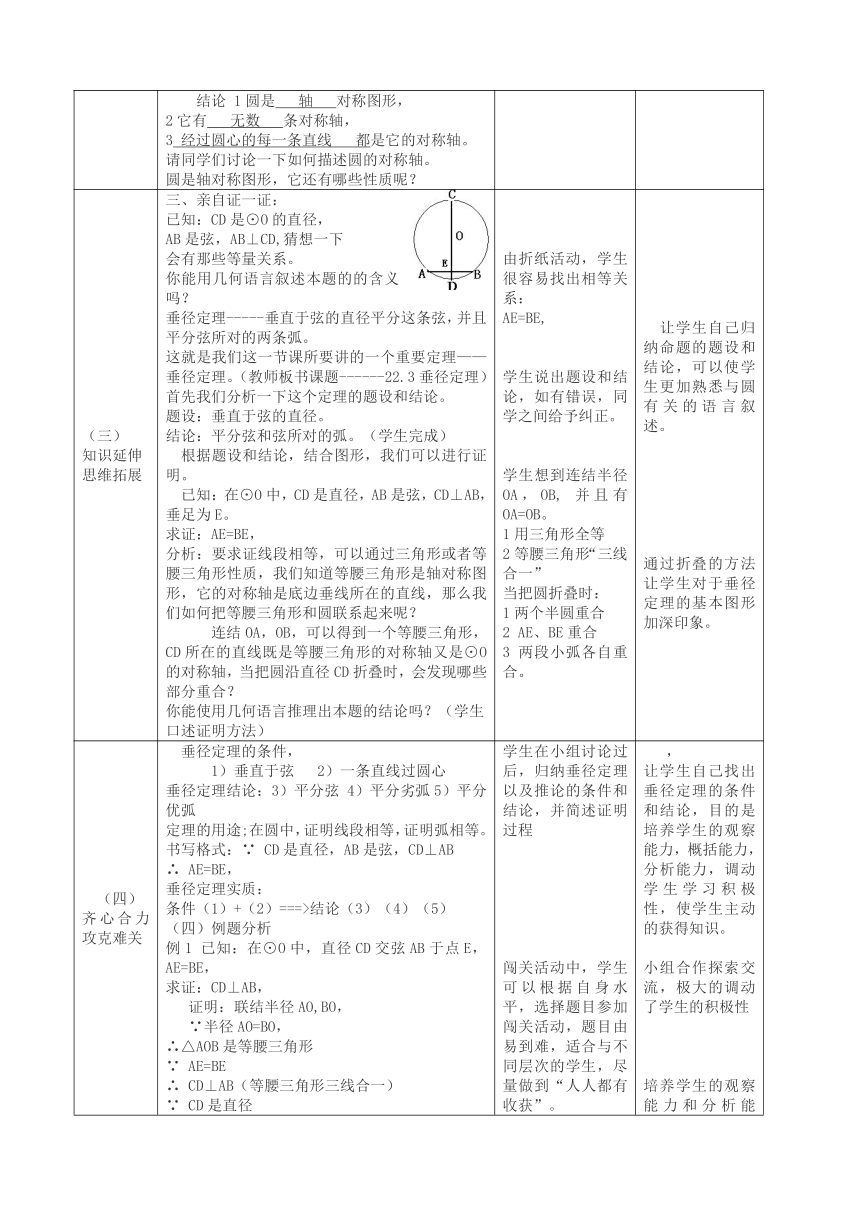
三、亲自证一证:
已知:CD是⊙O的直径,
AB是弦,AB⊥CD,猜想一下
会有那些等量关系。
你能用几何语言叙述本题的的含义吗?
垂径定理-----垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
这就是我们这一节课所要讲的一个重要定理——垂径定理。(教师板书课题------22.3垂径定理)
首先我们分析一下这个定理的题设和结论。
题设:垂直于弦的直径。
结论:平分弦和弦所对的弧。(学生完成)
?根据题设和结论,结合图形,我们可以进行证明。
?已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
求证:AE=BE, ?
分析:要求证线段相等,可以通过三角形或者等腰三角形性质,我们知道等腰三角形是轴对称图形,它的对称轴是底边垂线所在的直线,那么我们如何把等腰三角形和圆联系起来呢?
? ? 连结OA,OB,可以得到一个等腰三角形,CD所在的直线既是等腰三角形的对称轴又是⊙O的对称轴,当把圆沿直径CD折叠时,会发现哪些部分重合?
你能使用几何语言推理出本题的结论吗?(学生
口述证明方法) 由折纸活动,学生很容易找出相等关系:
AE=BE,
?
?
学生说出题设和结论,如有错误,同学之间给予纠正。
?
?
学生想到连结半径OA,OB, 并且有OA=OB。
1用三角形全等
2等腰三角形“三线合一”
当把圆折叠时:
1两个半圆重合
2 AE、BE重合
3 两段小弧各自重合。 ?
?让学生自己归纳命题的题设和结论,可以使学生更加熟悉与圆有关的语言叙述。
?
?
?
?
?
?
通过折叠的方法让学生对于垂径定理的基本图形加深印象。
?(四) 齐心合力攻克难关
? ?垂径定理的条件,
1)垂直于弦? 2)一条直线过圆心?
垂径定理结论:3)平分弦 4)平分劣弧5)平分优弧
定理的用途;在圆中,证明线段相等,证明弧相等。
书写格式:∵ CD是直径,AB是弦,CD⊥AB
∴ AE=BE, ?
垂径定理实质:
条件(1)+(2)===>结论(3)(4)(5)
(四)例题分析
例1 已知:在⊙O中,直径CD交弦AB于点E,AE=BE,
求证:CD⊥AB,
? 证明:联结半径AO,BO,
? ∵半径AO=BO,
∴△AOB是等腰三角形
∵ AE=BE
∴ CD⊥AB(等腰三角形三线合一)
∵ CD是直径
∴ ? (垂径定理)
思考题:本题中为什么强调这条弦不是直径?
?垂径定理推论:? ?
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
?
垂径定理推论的实质:
条件(2)+(3)===>结论(1)(4)(5)
书写格式:(1)∵AE=BE, CD为过圆心的直线,
? ∴CD⊥AB, ?
(四)共同议一议:
?
看下列命题是否是真命题,如果是,请证明,如果不是,请举出反例。
?
1弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
2平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
?
以上两个命题都是真命题,他们都是垂径定理的推论,
命题1实质:条件(1)+(3)==>结论(2)(4)(5)?
书写格式:(1)∵AE=BE,,CD⊥AB
∴ CD过圆心, ?
命题2实质:条件(2)+(4)==>结论(1)(3)(5)
书写格式:(2)∵ CD是直径, ,
∴? CD⊥AB ,AE=BE,
? 上述命题1、2也是垂径定理的推论内容,,
实际上,这五个条件,任意选择其中两个,都可以推出另外三个结论。
垂径定理和它的推论是我们证明与圆有关的弦、弧、线段相等的重要方法之一, 学生在小组讨论过后,归纳垂径定理以及推论的条件和结论,并简述证明过程
??
?
?
?
?
?
闯关活动中,学生可以根据自身水平,选择题目参加闯关活动,题目由易到难,适合与不同层次的学生,尽量做到“人人都有收获”。
?
?
学生说出两个命题的题设和结论,并进行简单的证明。
?
?
?
学生小组讨论后回答。
?
?
?
学生归纳出垂径定理的规律以及定理的用途,为今后解决实际问题奠定基础
?
学生踊跃回答问题 ? ,
让学生自己找出垂径定理的条件和结论,目的是培养学生的观察能力,概括能力,分析能力,调动学生学习积极性,使学生主动的获得知识。
?
小组合作探索交流,极大的调动了学生的积极性
? ?
?
?
培养学生的观察能力和分析能力,以及解决问题的能力。
?
?
总结规律,培养学生的归纳总结能力。
?
培养学生的灵活运用能力。
?
总结规律,使学生把知识归入体系。发散思维,开阔学生的想象空间,从而培养学生的创造能力,和创造思维。
?
?
通过实际问题的结决,使学生会用所学的知识解决日常生活中的有关问题,从而使数学真正的为生活所用。
?
?(五) PK知识大舞台? 五、赛一赛,谁最快
(1)判断下列语句是否正确。
? 1、平分弦的直径,平分这条弦所对的弧。(? )
? 2、平分弦的直线,必定过圆心。(? )
? 3、一条直线平分弦(这条弦不是直径),那么这条直线垂直这条弦。 (? )
? 4、弦的垂直平分线一定是圆的直径。(? )
? 5、平分弧的直线,平分这条弧所对的 弦。(? )
? 6、弦垂直于直径,这条直径就被弦平分。(? )
(2) 看图填空:
?∵ CD是直径,CD⊥AB
∴ ? ? ? ? ? ? ? ? ? ???
∵ CD是直径, AE=BE
∴, ? ? ? ? ? ? ? ? ? ?
?∵? AE=BE,CD⊥AB
∴ ?? ? ? ? ? ? ? ? ? ?
④∵ CD是直径,
∴ ? ? ? ? ? ? ? ? ? ??
?(4)你能画出使用垂径定理的相关图形码?
?
? ?
?
?
?
?
?
?
学生积极动脑参与,共同学习新的知识
?
?
?
?
?
?
? ?
?
?
?
?
?
? 赛一赛环节使学生进一步熟悉垂径定理的使用条件。并把所学的知识纳入已有的知识体系。
?
?
?
?
?
(六) 知识梳理 ? 本节课我们都学习了哪些内容?
1圆是轴对称图形
2垂径定理及推论。
3 垂径定理的书写格式和用途。?
4 你掌握了------?
5 你有哪些困惑------? ?学生总结本节课的内容,提出知识要点。 ?学生自己整理知识,有利于他们完善自己的数学体系,也有利于提高他们的整合知识的能力和概括能力。
(七) 课后作业 三级跳的中与垂径定理有关的内容
(八) 板书设计 垂径定理
1垂径定理内容? ? ? ? ? ? ? 2垂径定理推论的内容? ? ? ? 3垂径定理常用的图形
书写格式? ? ? ? ? ? ? ? ? ? ? ? ? ? 书写格式
定理用途? ? ? ? ? ? ? ? ? ? ? ? ? ? 定理用途
课时 第一课时 教学方法 小组合作,探索交流
教材 北师大版九年级数学下册第三章圆
教学目标 1知识技能目标:
? 理解垂径定理和推论的内容,并会证明,掌握弦、弧、直径之间的特定关系,并会利用垂径定理解决与圆有关问题。
2过程方法目标:
? 经历探索垂径定理和推论的证明过程,掌握从特殊到一般,由猜测到论证的证明思路。
学会与人合作探索获得新知识的一些方法。
3情感态度与价值观:
? 通过参与垂径定理的数学活动,体会垂径定理的重要性,品尝成功的经验,体验数学活动充满着探索和创造。
教学重点 1 垂径定理以及推论的证明,
2 垂径定理的简单应用,
教学难点 ? ?垂径定理及其推论的正确区分及运用
教学方法 讨论法、探索法
教学用具 ? ? 多媒体 ,? 投影仪
教? 学? 过? 程
教学环节 教师活动 学生活动 教学意图
(一) 创设情境
引入新知
? 一、动脑想一想(出示幻灯片)
1请欣赏下列图片,并思考这些美丽的图案有什么共同特征?
?
2我们学过图形中轴对称图形有哪些?
? 它们各有几条对称轴呢?
3圆是不是轴对称图形呢?我们今天就来研究它。
? 学生通过观察,指出他们都是轴对称图形,并指出对称轴。
?学生答:线段、等腰三角形,等边三角形,矩形,菱形,正方形,等腰梯形,圆。
?
学生通过折纸活动,很容易答出:圆是轴对称图形。它有无数条对称轴,对称轴是-----?
学生答案1:它的直径。、
学生答案2:经过圆心的直线 由图片引出轴对称的知识,并将其引入圆中来,可以使学生更深刻的体会生活中处处蕴含着数学.
回顾学过的几何图形的对称性,为下面学习圆的对称性做铺垫,
通过折纸活动,训练和提高学生的动手实践能力以及空间想象能力,为解决折叠问题提供思路,
?
强化对称轴是一条直线的概念。训练学生使用准确的数学语言描述问题。
(二) 动手实践,合作探索 二、动手折一折
? ? 请同学们拿出事先准备好的圆形纸片,按老师的要求来做。
在圆形纸片上任意画一条直径,然后把这个圆形纸片沿着这条直径对折,观察折叠后的两个半圆有何关系?最后得出什么结论?(填空)
??结论 1圆是? 轴 ?对称图形,
2它有? 无数? 条对称轴,
3 经过圆心的每一条直线? 都是它的对称轴。
请同学们讨论一下如何描述圆的对称轴。
圆是轴对称图形,它还有哪些性质呢?
(三) 知识延伸
思维拓展
三、亲自证一证:
已知:CD是⊙O的直径,
AB是弦,AB⊥CD,猜想一下
会有那些等量关系。
你能用几何语言叙述本题的的含义吗?
垂径定理-----垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
这就是我们这一节课所要讲的一个重要定理——垂径定理。(教师板书课题------22.3垂径定理)
首先我们分析一下这个定理的题设和结论。
题设:垂直于弦的直径。
结论:平分弦和弦所对的弧。(学生完成)
?根据题设和结论,结合图形,我们可以进行证明。
?已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
求证:AE=BE, ?
分析:要求证线段相等,可以通过三角形或者等腰三角形性质,我们知道等腰三角形是轴对称图形,它的对称轴是底边垂线所在的直线,那么我们如何把等腰三角形和圆联系起来呢?
? ? 连结OA,OB,可以得到一个等腰三角形,CD所在的直线既是等腰三角形的对称轴又是⊙O的对称轴,当把圆沿直径CD折叠时,会发现哪些部分重合?
你能使用几何语言推理出本题的结论吗?(学生
口述证明方法) 由折纸活动,学生很容易找出相等关系:
AE=BE,
?
?
学生说出题设和结论,如有错误,同学之间给予纠正。
?
?
学生想到连结半径OA,OB, 并且有OA=OB。
1用三角形全等
2等腰三角形“三线合一”
当把圆折叠时:
1两个半圆重合
2 AE、BE重合
3 两段小弧各自重合。 ?
?让学生自己归纳命题的题设和结论,可以使学生更加熟悉与圆有关的语言叙述。
?
?
?
?
?
?
通过折叠的方法让学生对于垂径定理的基本图形加深印象。
?(四) 齐心合力攻克难关
? ?垂径定理的条件,
1)垂直于弦? 2)一条直线过圆心?
垂径定理结论:3)平分弦 4)平分劣弧5)平分优弧
定理的用途;在圆中,证明线段相等,证明弧相等。
书写格式:∵ CD是直径,AB是弦,CD⊥AB
∴ AE=BE, ?
垂径定理实质:
条件(1)+(2)===>结论(3)(4)(5)
(四)例题分析
例1 已知:在⊙O中,直径CD交弦AB于点E,AE=BE,
求证:CD⊥AB,
? 证明:联结半径AO,BO,
? ∵半径AO=BO,
∴△AOB是等腰三角形
∵ AE=BE
∴ CD⊥AB(等腰三角形三线合一)
∵ CD是直径
∴ ? (垂径定理)
思考题:本题中为什么强调这条弦不是直径?
?垂径定理推论:? ?
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
?
垂径定理推论的实质:
条件(2)+(3)===>结论(1)(4)(5)
书写格式:(1)∵AE=BE, CD为过圆心的直线,
? ∴CD⊥AB, ?
(四)共同议一议:
?
看下列命题是否是真命题,如果是,请证明,如果不是,请举出反例。
?
1弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
2平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。
?
以上两个命题都是真命题,他们都是垂径定理的推论,
命题1实质:条件(1)+(3)==>结论(2)(4)(5)?
书写格式:(1)∵AE=BE,,CD⊥AB
∴ CD过圆心, ?
命题2实质:条件(2)+(4)==>结论(1)(3)(5)
书写格式:(2)∵ CD是直径, ,
∴? CD⊥AB ,AE=BE,
? 上述命题1、2也是垂径定理的推论内容,,
实际上,这五个条件,任意选择其中两个,都可以推出另外三个结论。
垂径定理和它的推论是我们证明与圆有关的弦、弧、线段相等的重要方法之一, 学生在小组讨论过后,归纳垂径定理以及推论的条件和结论,并简述证明过程
??
?
?
?
?
?
闯关活动中,学生可以根据自身水平,选择题目参加闯关活动,题目由易到难,适合与不同层次的学生,尽量做到“人人都有收获”。
?
?
学生说出两个命题的题设和结论,并进行简单的证明。
?
?
?
学生小组讨论后回答。
?
?
?
学生归纳出垂径定理的规律以及定理的用途,为今后解决实际问题奠定基础
?
学生踊跃回答问题 ? ,
让学生自己找出垂径定理的条件和结论,目的是培养学生的观察能力,概括能力,分析能力,调动学生学习积极性,使学生主动的获得知识。
?
小组合作探索交流,极大的调动了学生的积极性
? ?
?
?
培养学生的观察能力和分析能力,以及解决问题的能力。
?
?
总结规律,培养学生的归纳总结能力。
?
培养学生的灵活运用能力。
?
总结规律,使学生把知识归入体系。发散思维,开阔学生的想象空间,从而培养学生的创造能力,和创造思维。
?
?
通过实际问题的结决,使学生会用所学的知识解决日常生活中的有关问题,从而使数学真正的为生活所用。
?
?(五) PK知识大舞台? 五、赛一赛,谁最快
(1)判断下列语句是否正确。
? 1、平分弦的直径,平分这条弦所对的弧。(? )
? 2、平分弦的直线,必定过圆心。(? )
? 3、一条直线平分弦(这条弦不是直径),那么这条直线垂直这条弦。 (? )
? 4、弦的垂直平分线一定是圆的直径。(? )
? 5、平分弧的直线,平分这条弧所对的 弦。(? )
? 6、弦垂直于直径,这条直径就被弦平分。(? )
(2) 看图填空:
?∵ CD是直径,CD⊥AB
∴ ? ? ? ? ? ? ? ? ? ???
∵ CD是直径, AE=BE
∴, ? ? ? ? ? ? ? ? ? ?
?∵? AE=BE,CD⊥AB
∴ ?? ? ? ? ? ? ? ? ? ?
④∵ CD是直径,
∴ ? ? ? ? ? ? ? ? ? ??
?(4)你能画出使用垂径定理的相关图形码?
?
? ?
?
?
?
?
?
?
学生积极动脑参与,共同学习新的知识
?
?
?
?
?
?
? ?
?
?
?
?
?
? 赛一赛环节使学生进一步熟悉垂径定理的使用条件。并把所学的知识纳入已有的知识体系。
?
?
?
?
?
(六) 知识梳理 ? 本节课我们都学习了哪些内容?
1圆是轴对称图形
2垂径定理及推论。
3 垂径定理的书写格式和用途。?
4 你掌握了------?
5 你有哪些困惑------? ?学生总结本节课的内容,提出知识要点。 ?学生自己整理知识,有利于他们完善自己的数学体系,也有利于提高他们的整合知识的能力和概括能力。
(七) 课后作业 三级跳的中与垂径定理有关的内容
(八) 板书设计 垂径定理
1垂径定理内容? ? ? ? ? ? ? 2垂径定理推论的内容? ? ? ? 3垂径定理常用的图形
书写格式? ? ? ? ? ? ? ? ? ? ? ? ? ? 书写格式
定理用途? ? ? ? ? ? ? ? ? ? ? ? ? ? 定理用途
