19.2.3一次函数与一元一次不等式 课件-2020-2021学年人教版八年级数学下册(17张)
文档属性
| 名称 | 19.2.3一次函数与一元一次不等式 课件-2020-2021学年人教版八年级数学下册(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 873.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 13:15:12 | ||
图片预览





文档简介
空白演示
单击输入您的封面副标题
19.2.3 一次函数与一元一次不等式
人教版数学八年级下册
练一练:
如图:当x——————一次函数y=x-2的值为0 ,
x=2是一元一次方程———————的解.
=2
x-2=0
3
2
x
-2
y
0
Y=x-2
4
当x=3时,函数y=x-2的值是-------
1
当x=4,函数y=x-2的值是--------
2
思考:当x为何值 时,
函数y=x-2对应
的值大于0 ?
上节课我们用函数观点,从数和形两个角度
学习了一元一次方程求解问题。
温故知新
y=2x-4
可以看出,当x>2时,直线上的点全在x轴的上方。
即:x>2时, y=2x-4 >0
所以2x-4>0的解集为x>2
由此可知:通过函数图像可以求不等式的解集
2
-4
x
y
0
同理: x< 2时, y=2x-4 < 0,所以2x-4<0的解集为x < 2
观察函数y=2x-4 的图像,
我们从函数图象来看看
探究新知
-2
x
y=3x+6
y
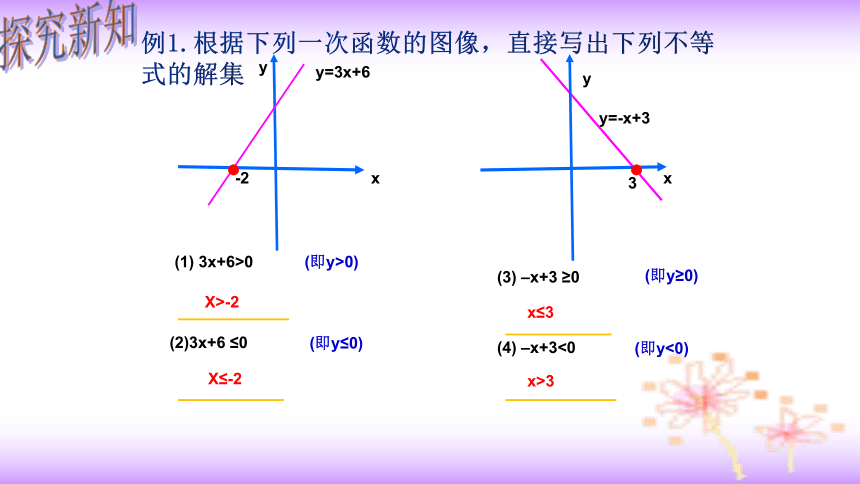
例1.根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
探究新知
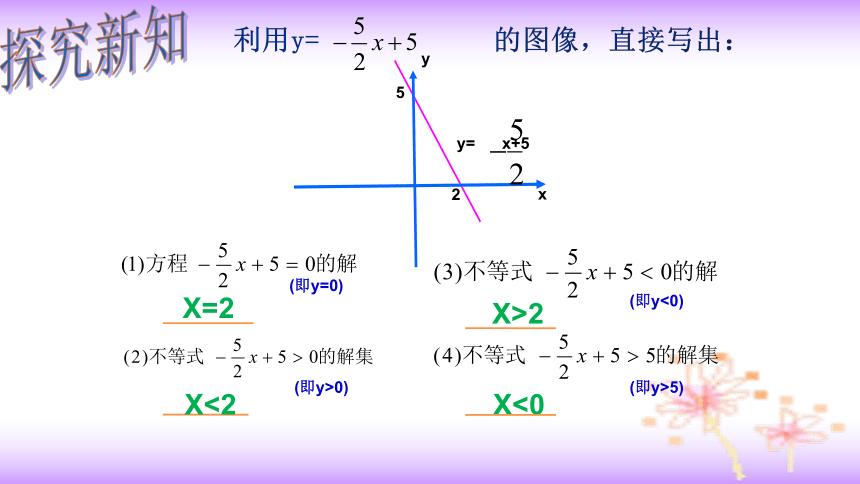
利用y= 的图像,直接写出:
y
2
5
x
y= x+5
X=2
X<2
X>2
X<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
探究新知
例2.用画函数图象的方法解不等式5x+4<2x+10
解法1:原不等式化为3x -6 <0,
画出直线y = 3x -6(如图)
可以看出,当x<2 时这条直线上
的点在X轴的下方,
即这时y = 3x -6 <0
所以不等式的解集为x<2
探究新知
解法二:画出函数 y = 2x+10 t和 y = 5x+4图象
从图中看出:当x <2时
直线 y = 5x +4 在 y = 2x +10的下方
即 5x+4 < 2x +10
∴ 不等式 5x+4 < 2 x +10 的解集是
x < 2
10
-5
y=2x+10
y=5x+4
2
x
y
0
14
4
两种解不等式的方法都是把不等式转化为比较直线上点的位置的高低
2
-6
x
y
0
y=3x-6
探究新知
x>2
1.如图是一次函数
的图象,则关于x的方程
的解为 ;关于x的不等式
的解集为 ;
的解集为 .
关于x的不等式
x=2
x<2
巩固练习
2.如右图, 一次函数
的图象
经过点 ,则关于x的不等等式 的解集为________________.
x<-2
巩固练习
3.看图象解不等式
x
o
y=5x-3
2
y=3x+1
7
y
从图中看出,当x>2时,直线y=5x-3上的点在直线y=3x+1上相应点的上方,即5x-3>3x+1,所以不等式的解集为x>2。
巩固练习
4..求当自变量x取值范围为什么时,
函数y=2x+6的值满足以下条件? ①y=0; ②y>0.
解:①方法一:y=0即y=2x+6=0 2x+6=0,解得x=-3.
方法二:作出直线y=2x+6的图象,
从图象上可以看出:直线y=2x+6与
x轴交于(-3,0),即x=-3时,y=2x+6=0.
②方法一:要使y>0,即y=2x+6>0.由2x+6>0,
解得,x>-3.
方法二:作出直线y=2x+6的图象.
从图象上可以看出:当x>-3时,
直线y=2x+6上的点都在x轴的上方,
即函数值大于0.所以当x>-3时,y>0.
巩固练习
5.利用图象解不等式5x-1>2x+5.
解:方法一:5x-1>2x+5可变形为:3x-6>0,
作出直线y=3x-6.由图象上可知
直线y=3x-6与x轴交于点(2,0).
当x>2时,直线y=3x-6上的点都在
x轴上方,即3x-6>0,
所以5x-1>2x-5的解为x>2.
方法二:分别作出直线y=5x-1与
直线y=2x+5的图象.由图象可知:
两直线交点的横坐标为2,当x>2时,
直线y=5x-1在直线y=2x+5的上方,
即5x-1>2x+5.所以它的解为x>2.
巩固练习
我们学校做一批校徽,需要拍照,若到照相馆拍,每张需要8元;若学校自己拍,除买摄象机,需120元,每张还需成本4元,设需要拍X张,到照相馆拍需要Y1 元,学校自己拍需要y2元。
1.求y1和y2与X的函数关系式
2.问拍这批照片到照相馆拍,费用省还是由学校自己拍费用省?请说明理由。
解:(1) y1=8x,y2=4x+120
(2)由图象可知,当x=30 时,两家一样,
当X>30时,照相馆省钱,
当X<30时,学校自己省钱.
30
y
x
0
Y=4x+120
Y=8x
拓展延伸
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在X轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
一次函数与一元一次不等式的关系
课堂小结
布置作业
教科书99页,习题 19.2 13题
教科书第60页第3、6题
布置作业
再见
单击输入您的封面副标题
19.2.3 一次函数与一元一次不等式
人教版数学八年级下册
练一练:
如图:当x——————一次函数y=x-2的值为0 ,
x=2是一元一次方程———————的解.
=2
x-2=0
3
2
x
-2
y
0
Y=x-2
4
当x=3时,函数y=x-2的值是-------
1
当x=4,函数y=x-2的值是--------
2
思考:当x为何值 时,
函数y=x-2对应
的值大于0 ?
上节课我们用函数观点,从数和形两个角度
学习了一元一次方程求解问题。
温故知新
y=2x-4
可以看出,当x>2时,直线上的点全在x轴的上方。
即:x>2时, y=2x-4 >0
所以2x-4>0的解集为x>2
由此可知:通过函数图像可以求不等式的解集
2
-4
x
y
0
同理: x< 2时, y=2x-4 < 0,所以2x-4<0的解集为x < 2
观察函数y=2x-4 的图像,
我们从函数图象来看看
探究新知
-2
x
y=3x+6
y
例1.根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
探究新知
利用y= 的图像,直接写出:
y
2
5
x
y= x+5
X=2
X<2
X>2
X<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
探究新知
例2.用画函数图象的方法解不等式5x+4<2x+10
解法1:原不等式化为3x -6 <0,
画出直线y = 3x -6(如图)
可以看出,当x<2 时这条直线上
的点在X轴的下方,
即这时y = 3x -6 <0
所以不等式的解集为x<2
探究新知
解法二:画出函数 y = 2x+10 t和 y = 5x+4图象
从图中看出:当x <2时
直线 y = 5x +4 在 y = 2x +10的下方
即 5x+4 < 2x +10
∴ 不等式 5x+4 < 2 x +10 的解集是
x < 2
10
-5
y=2x+10
y=5x+4
2
x
y
0
14
4
两种解不等式的方法都是把不等式转化为比较直线上点的位置的高低
2
-6
x
y
0
y=3x-6
探究新知
x>2
1.如图是一次函数
的图象,则关于x的方程
的解为 ;关于x的不等式
的解集为 ;
的解集为 .
关于x的不等式
x=2
x<2
巩固练习
2.如右图, 一次函数
的图象
经过点 ,则关于x的不等等式 的解集为________________.
x<-2
巩固练习
3.看图象解不等式
x
o
y=5x-3
2
y=3x+1
7
y
从图中看出,当x>2时,直线y=5x-3上的点在直线y=3x+1上相应点的上方,即5x-3>3x+1,所以不等式的解集为x>2。
巩固练习
4..求当自变量x取值范围为什么时,
函数y=2x+6的值满足以下条件? ①y=0; ②y>0.
解:①方法一:y=0即y=2x+6=0 2x+6=0,解得x=-3.
方法二:作出直线y=2x+6的图象,
从图象上可以看出:直线y=2x+6与
x轴交于(-3,0),即x=-3时,y=2x+6=0.
②方法一:要使y>0,即y=2x+6>0.由2x+6>0,
解得,x>-3.
方法二:作出直线y=2x+6的图象.
从图象上可以看出:当x>-3时,
直线y=2x+6上的点都在x轴的上方,
即函数值大于0.所以当x>-3时,y>0.
巩固练习
5.利用图象解不等式5x-1>2x+5.
解:方法一:5x-1>2x+5可变形为:3x-6>0,
作出直线y=3x-6.由图象上可知
直线y=3x-6与x轴交于点(2,0).
当x>2时,直线y=3x-6上的点都在
x轴上方,即3x-6>0,
所以5x-1>2x-5的解为x>2.
方法二:分别作出直线y=5x-1与
直线y=2x+5的图象.由图象可知:
两直线交点的横坐标为2,当x>2时,
直线y=5x-1在直线y=2x+5的上方,
即5x-1>2x+5.所以它的解为x>2.
巩固练习
我们学校做一批校徽,需要拍照,若到照相馆拍,每张需要8元;若学校自己拍,除买摄象机,需120元,每张还需成本4元,设需要拍X张,到照相馆拍需要Y1 元,学校自己拍需要y2元。
1.求y1和y2与X的函数关系式
2.问拍这批照片到照相馆拍,费用省还是由学校自己拍费用省?请说明理由。
解:(1) y1=8x,y2=4x+120
(2)由图象可知,当x=30 时,两家一样,
当X>30时,照相馆省钱,
当X<30时,学校自己省钱.
30
y
x
0
Y=4x+120
Y=8x
拓展延伸
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在X轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
一次函数与一元一次不等式的关系
课堂小结
布置作业
教科书99页,习题 19.2 13题
教科书第60页第3、6题
布置作业
再见
