2020-2021学年八年级数学北师大版下册 第四章 因式分解 同步单元训练卷(word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册 第四章 因式分解 同步单元训练卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 70.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 00:00:00 | ||
图片预览


文档简介
北师大版八年级数学下册
第四章
因式分解
同步单元训练卷
一、选择题(共10小题,3
10=30)
1.多项式9a2x2-18a3x3-36a4x4各项的公因式是(
)
A.a2x2
B.a3x3
C.9a2x2
D.9a4x4
2.下列各式由左边到右边的变形中,是因式分解的为(
)
A.m(x+y)=mx+my
B.8x2-4x=4x(2x-1)
C.x2-6x+5=x(x-6)+5
D.x2-9+2x=(x+3)(x-3)+2x
3.下列因式分解错误的是(
)
A.
2a﹣2b=2(a﹣b)
B.
x2﹣9=(x+3)(x﹣3)
C.
a2+4a﹣4=(a+2)2
D.
﹣x2﹣x+2=﹣(x﹣1)(x+2)
4.下列多项式中不能用公式法分解的是(
)
A.-a2-b2+2ab
B.a2+a+
C.-a2+25b2
D.-4-b2
5.下列因式分解正确的是( )
A.3ax2-6ax=3(ax2-2ax)
B.x2+y2=(-x+y)(-x-y)
C.a2+2ab-4b2=(a+2b)2
D.-ax2+2ax-a=-a(x-1)2
6.
若x2+kx-15=(x+3)(x+m),则k-m的值为( )
A.-3
B.3
C.-2
D.2
7.已知△ABC的三边长分别为a,b,c,且满足a2+b2+c2=ab+ac+bc,则△ABC的形状是( )
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等边三角形
8.计算(-2)99+(-2)100的结果为(
)
A.299
B.2100
C.-299
D.-2
9.若9x2+kx+16是一个完全平方式,则k的值等于(
)
A.12
B.24
C.-24
D.±24
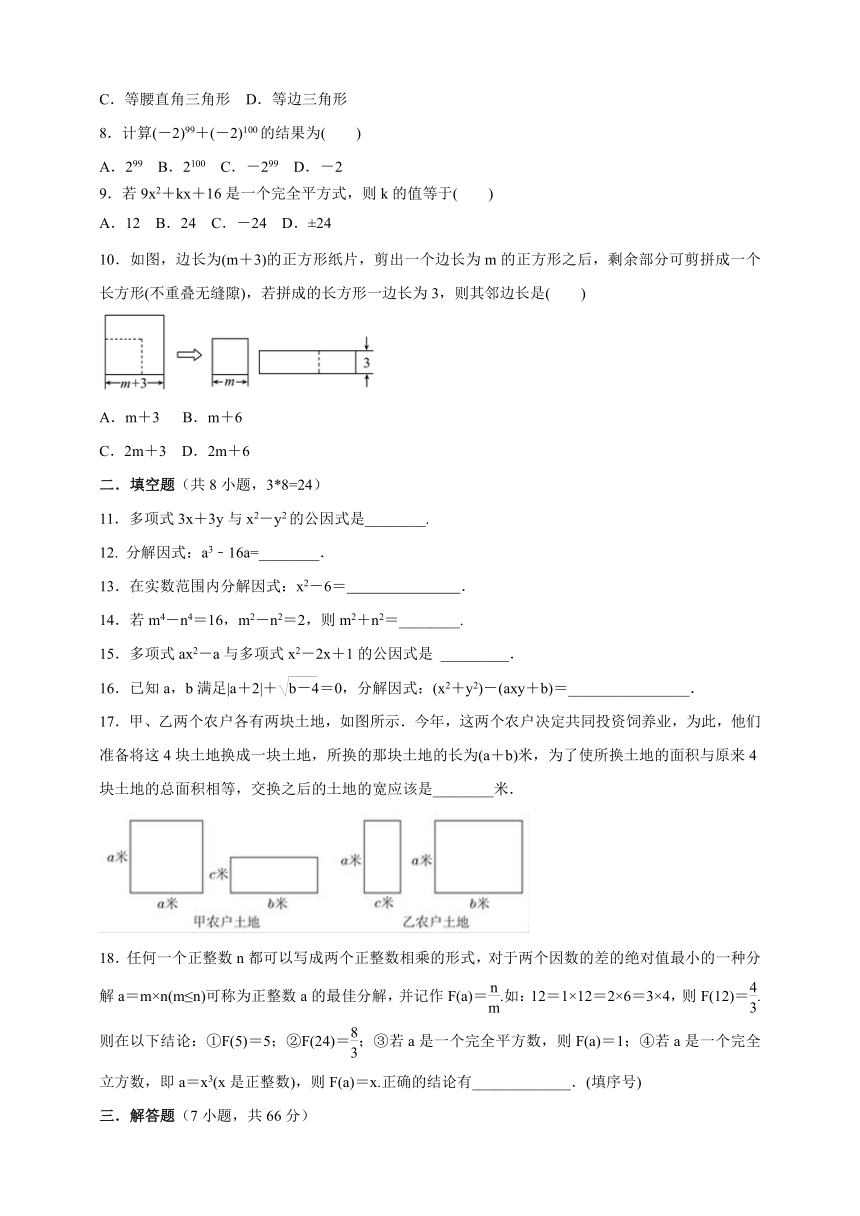
10.如图,边长为(m+3)的正方形纸片,剪出一个边长为m的正方形之后,剩余部分可剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则其邻边长是(
)
A.m+3
B.m+6
C.2m+3
D.2m+6
二.填空题(共8小题,3
8=24)
11.多项式3x+3y与x2-y2的公因式是________.
12.
分解因式:a3﹣16a=________.
13.在实数范围内分解因式:x2-6=
.
14.若m4-n4=16,m2-n2=2,则m2+n2=________.
15.多项式ax2-a与多项式x2-2x+1的公因式是
_________.
16.已知a,b满足|a+2|+=0,分解因式:(x2+y2)-(axy+b)=________________.
17.甲、乙两个农户各有两块土地,如图所示.今年,这两个农户决定共同投资饲养业,为此,他们准备将这4块土地换成一块土地,所换的那块土地的长为(a+b)米,为了使所换土地的面积与原来4块土地的总面积相等,交换之后的土地的宽应该是________米.
18.任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)=.如:12=1×12=2×6=3×4,则F(12)=.则在以下结论:①F(5)=5;②F(24)=;③若a是一个完全平方数,则F(a)=1;④若a是一个完全立方数,即a=x3(x是正整数),则F(a)=x.正确的结论有_____________.(填序号)
三.解答题(7小题,共66分)
19.(8分)
将下列各式分解因式:
(1)2x2y-8xy+8y;
(2)a2(x-y)-9b2(x-y).
20.(8分)
将如图一个正方形和三个长方形拼成一个大长方形,再据此图写出一个多项式的因式分解.
21.(8分)
若|m+4|与n2-2n+1互为相反数,把多项式x2+4y2-mxy-n分解因式.
22.(10分)
利用因式分解计算:
(1)0.3332×4-1.2222×9;
(2)4002-800×398+3982.
23.(10分)
已知a2+5a+1=0,求多项式a5+7a4+14a3+18a2+8a+8的值.
24.(10分)
先阅读下列材料,再解答问题:
材料:因式分解:(x+y)2+2(x+y)+1.
解:将“x+y”看成整体,令x+y=A,
则原式=A2+2A+1=(A+1)2.
再将“A”还原,得原式=(x+y+1)2.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你解答下列问题:
(1)分解因式:1+2(x-y)+(x-y)2=____________;
(2)分解因式:(a+b)(a+b-4)+4;
(3)求证:若n为正整数,则式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.
25.(12分)
观察猜想:
如图,大长方形是由三个小长方形和一个正方形拼成的,请根据此图填空:
x2+(p+q)x+pq=x2+px+qx+pq=(__________)(__________).
说理验证:
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq=x2+px+qx+pq=(x2+px)+(qx+pq)=__________________=(________)(________).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用:
例题:把x2+3x+2因式分解.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式因式分解:
(1)x2-7x+12;
(2)(y2+y)2+7(y2+y)-18.
参考答案
1-5CBCDD
6-10BDADC
11.
x+y
12.
a(a+4)(a﹣4)
13.(x-)(x+)
14.
8
15.
x-1
16.(x+y+2)(x+y-2)
17.(a+c)
18.
①③
19.
解:(1)原式=2y(x-2)2
(2)
原式=
(x-y)(a+3b)(a-3b)
20.
解:拼接如图:
长方形的面积为:x2+3x+2,还可以表示面积为:(x+2)(x+1),∴我们得到了可以进行因式分解的公式:x2+3x+2=(x+2)(x+1)
21.
解:由题意,得|m+4|+(n-1)2=0,∴解得∴x2+4y2-mxy-n=x2+4y2+4xy-1=(x+2y)2-1,=(x+2y+1)(x+2y-1).
22.
解:(1)-12.996 (2)4
23.
解:∵a2+5a+1=0,∴原式=a5+5a4+a3+2a4+10a3+2a2+3a3+15a2+3a+a2+5a+1+7=a3(a2+5a+1)+2a2(a2+5a+1)+3a(a2+5a+1)+(a2+5a+1)+7=7.
24.
(1)(x-y+1)2
(2)解:令a+b=A,则原式变为A(A-4)+4=A2-4A+4=(A-2)2.
故(a+b)(a+b-4)+4=(a+b-2)2.
(3)证明:(n+1)(n+2)(n2+3n)+1=(n2+3n)[(n+1)(n+2)]+1=(n2+3n)(n2+3n+2)+1=(n2+3n)2+2(n2+3n)+1=(n2+3n+1)2.
∵n为正整数,∴n2+3n+1也为正整数.∴式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.
25.解:x+p;x+q;
x(x+p)+q(x+p);x+p;x+q
(1)原式=(x-3)(x-4).
(2)原式=(y2+y+9)(y2+y-2)=(y2+y+9)(y+2)(y-1).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
第四章
因式分解
同步单元训练卷
一、选择题(共10小题,3
10=30)
1.多项式9a2x2-18a3x3-36a4x4各项的公因式是(
)
A.a2x2
B.a3x3
C.9a2x2
D.9a4x4
2.下列各式由左边到右边的变形中,是因式分解的为(
)
A.m(x+y)=mx+my
B.8x2-4x=4x(2x-1)
C.x2-6x+5=x(x-6)+5
D.x2-9+2x=(x+3)(x-3)+2x
3.下列因式分解错误的是(
)
A.
2a﹣2b=2(a﹣b)
B.
x2﹣9=(x+3)(x﹣3)
C.
a2+4a﹣4=(a+2)2
D.
﹣x2﹣x+2=﹣(x﹣1)(x+2)
4.下列多项式中不能用公式法分解的是(
)
A.-a2-b2+2ab
B.a2+a+
C.-a2+25b2
D.-4-b2
5.下列因式分解正确的是( )
A.3ax2-6ax=3(ax2-2ax)
B.x2+y2=(-x+y)(-x-y)
C.a2+2ab-4b2=(a+2b)2
D.-ax2+2ax-a=-a(x-1)2
6.
若x2+kx-15=(x+3)(x+m),则k-m的值为( )
A.-3
B.3
C.-2
D.2
7.已知△ABC的三边长分别为a,b,c,且满足a2+b2+c2=ab+ac+bc,则△ABC的形状是( )
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等边三角形
8.计算(-2)99+(-2)100的结果为(
)
A.299
B.2100
C.-299
D.-2
9.若9x2+kx+16是一个完全平方式,则k的值等于(
)
A.12
B.24
C.-24
D.±24
10.如图,边长为(m+3)的正方形纸片,剪出一个边长为m的正方形之后,剩余部分可剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为3,则其邻边长是(
)
A.m+3
B.m+6
C.2m+3
D.2m+6
二.填空题(共8小题,3
8=24)
11.多项式3x+3y与x2-y2的公因式是________.
12.
分解因式:a3﹣16a=________.
13.在实数范围内分解因式:x2-6=
.
14.若m4-n4=16,m2-n2=2,则m2+n2=________.
15.多项式ax2-a与多项式x2-2x+1的公因式是
_________.
16.已知a,b满足|a+2|+=0,分解因式:(x2+y2)-(axy+b)=________________.
17.甲、乙两个农户各有两块土地,如图所示.今年,这两个农户决定共同投资饲养业,为此,他们准备将这4块土地换成一块土地,所换的那块土地的长为(a+b)米,为了使所换土地的面积与原来4块土地的总面积相等,交换之后的土地的宽应该是________米.
18.任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)=.如:12=1×12=2×6=3×4,则F(12)=.则在以下结论:①F(5)=5;②F(24)=;③若a是一个完全平方数,则F(a)=1;④若a是一个完全立方数,即a=x3(x是正整数),则F(a)=x.正确的结论有_____________.(填序号)
三.解答题(7小题,共66分)
19.(8分)
将下列各式分解因式:
(1)2x2y-8xy+8y;
(2)a2(x-y)-9b2(x-y).
20.(8分)
将如图一个正方形和三个长方形拼成一个大长方形,再据此图写出一个多项式的因式分解.
21.(8分)
若|m+4|与n2-2n+1互为相反数,把多项式x2+4y2-mxy-n分解因式.
22.(10分)
利用因式分解计算:
(1)0.3332×4-1.2222×9;
(2)4002-800×398+3982.
23.(10分)
已知a2+5a+1=0,求多项式a5+7a4+14a3+18a2+8a+8的值.
24.(10分)
先阅读下列材料,再解答问题:
材料:因式分解:(x+y)2+2(x+y)+1.
解:将“x+y”看成整体,令x+y=A,
则原式=A2+2A+1=(A+1)2.
再将“A”还原,得原式=(x+y+1)2.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你解答下列问题:
(1)分解因式:1+2(x-y)+(x-y)2=____________;
(2)分解因式:(a+b)(a+b-4)+4;
(3)求证:若n为正整数,则式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.
25.(12分)
观察猜想:
如图,大长方形是由三个小长方形和一个正方形拼成的,请根据此图填空:
x2+(p+q)x+pq=x2+px+qx+pq=(__________)(__________).
说理验证:
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq=x2+px+qx+pq=(x2+px)+(qx+pq)=__________________=(________)(________).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用:
例题:把x2+3x+2因式分解.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式因式分解:
(1)x2-7x+12;
(2)(y2+y)2+7(y2+y)-18.
参考答案
1-5CBCDD
6-10BDADC
11.
x+y
12.
a(a+4)(a﹣4)
13.(x-)(x+)
14.
8
15.
x-1
16.(x+y+2)(x+y-2)
17.(a+c)
18.
①③
19.
解:(1)原式=2y(x-2)2
(2)
原式=
(x-y)(a+3b)(a-3b)
20.
解:拼接如图:
长方形的面积为:x2+3x+2,还可以表示面积为:(x+2)(x+1),∴我们得到了可以进行因式分解的公式:x2+3x+2=(x+2)(x+1)
21.
解:由题意,得|m+4|+(n-1)2=0,∴解得∴x2+4y2-mxy-n=x2+4y2+4xy-1=(x+2y)2-1,=(x+2y+1)(x+2y-1).
22.
解:(1)-12.996 (2)4
23.
解:∵a2+5a+1=0,∴原式=a5+5a4+a3+2a4+10a3+2a2+3a3+15a2+3a+a2+5a+1+7=a3(a2+5a+1)+2a2(a2+5a+1)+3a(a2+5a+1)+(a2+5a+1)+7=7.
24.
(1)(x-y+1)2
(2)解:令a+b=A,则原式变为A(A-4)+4=A2-4A+4=(A-2)2.
故(a+b)(a+b-4)+4=(a+b-2)2.
(3)证明:(n+1)(n+2)(n2+3n)+1=(n2+3n)[(n+1)(n+2)]+1=(n2+3n)(n2+3n+2)+1=(n2+3n)2+2(n2+3n)+1=(n2+3n+1)2.
∵n为正整数,∴n2+3n+1也为正整数.∴式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.
25.解:x+p;x+q;
x(x+p)+q(x+p);x+p;x+q
(1)原式=(x-3)(x-4).
(2)原式=(y2+y+9)(y2+y-2)=(y2+y+9)(y+2)(y-1).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
