2020-2021学年沪科 版 八年级数学下册19.3.2菱形的判定课件(24张)
文档属性
| 名称 | 2020-2021学年沪科 版 八年级数学下册19.3.2菱形的判定课件(24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 614.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 13:15:15 | ||
图片预览






文档简介
菱形的判定
聪明的同学们,你能剪出这些美丽的图案吗?
观 察
菱形就在我们身边
学习目标
?? 1、经历菱形的判定方法的探究过程,掌握菱形的三种判定方法??,能根据题目中的条件选择恰当的方法判定四边形是菱形。
?
2、培养学生操作能力和观察、猜想、推理的意识;
体会类比与转化的数学思想。
3、培养合作意识;养成严密的数学逻辑思维习惯.
??
学习重、难点
重点:菱形的判定定理的探究。
难点:菱形的判定定理的探究和应用。
一组邻边相等
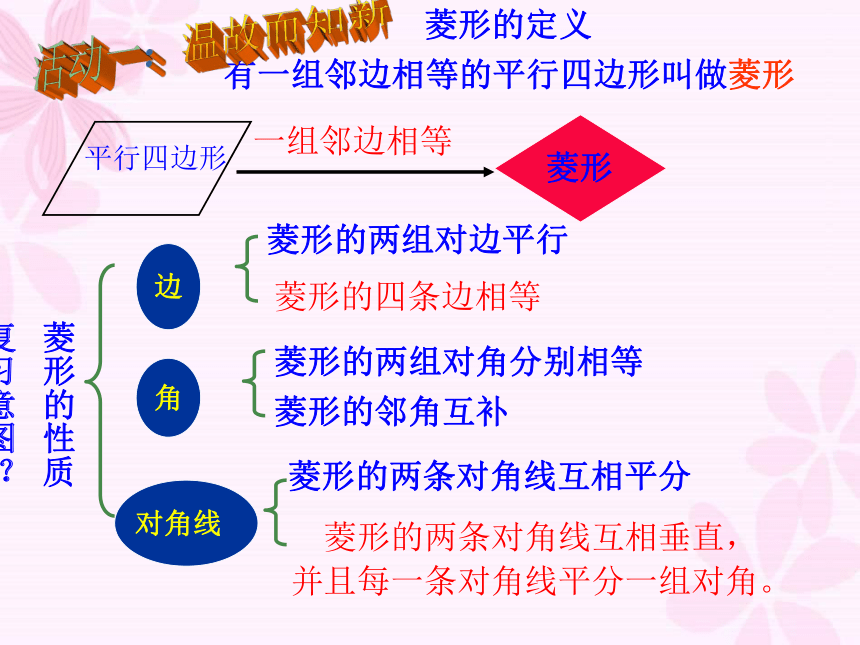
有一组邻边相等的平行四边形叫做菱形
平行四边形
边
对角线
角
菱形的定义
菱形的性质
复习意图?
菱形
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。
活动一:温故而知新
活动二
同学们,想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
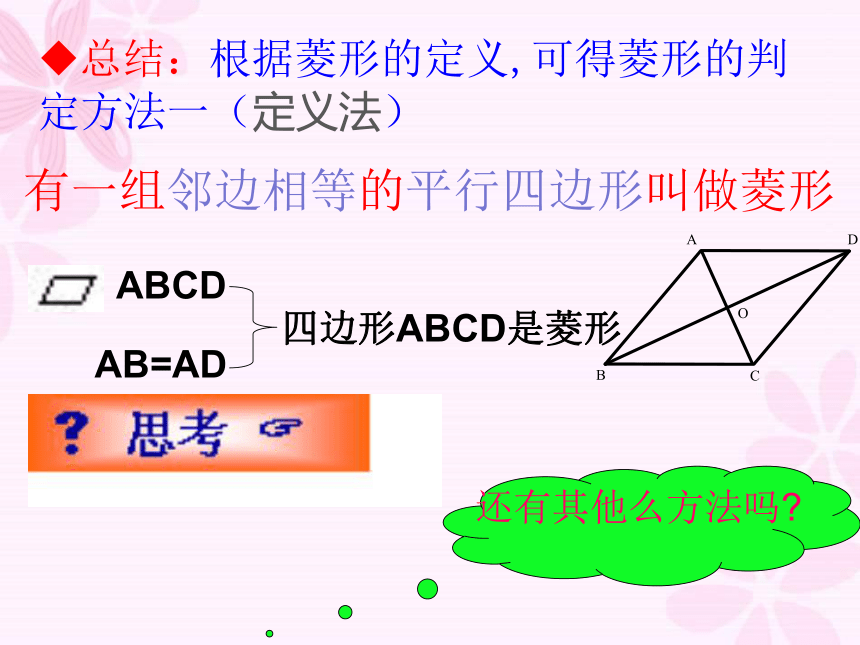
总结:根据菱形的定义,可得菱形的判定方法一(定义法)
有一组邻边相等的平行四边形叫做菱形
还有其他么方法吗?
ABCD
AB=AD
四边形ABCD是菱形
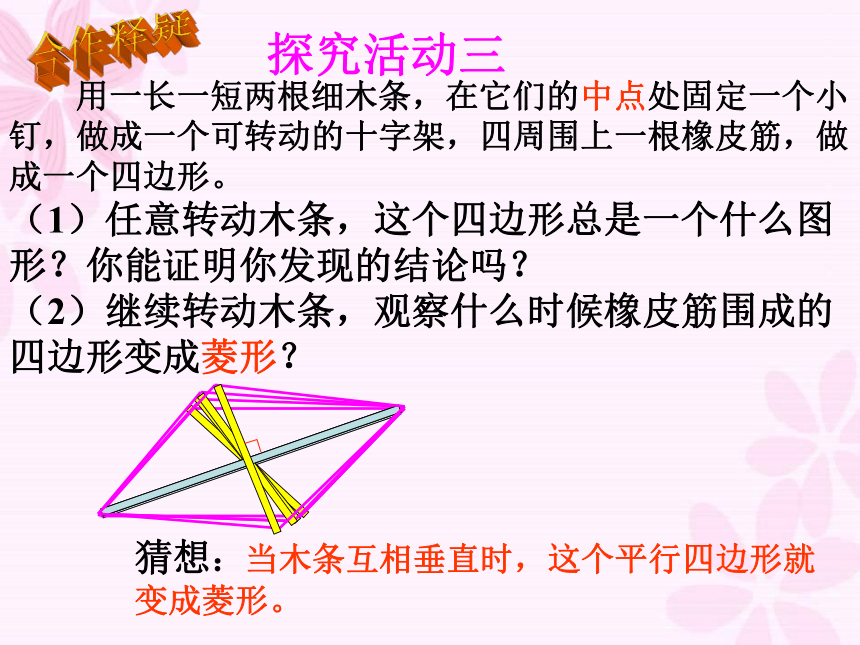
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可转动的十字架,四周围上一根橡皮筋,做成一个四边形。
(1)任意转动木条,这个四边形总是一个什么图形?你能证明你发现的结论吗?
(2)继续转动木条,观察什么时候橡皮筋围成的四边形变成菱形?
猜想:当木条互相垂直时,这个平行四边形就变成菱形。
合作释疑
∟
探究活动三
命题:对角线互相垂直的平行四边形是菱形.
A
B
C
D
已知:在 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
证明:
∴ ABCD是菱形
又∵ AC ⊥ BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
O
定理:对角线互相垂直的平行四边形是菱形.
判定方法2:
对角线互相垂直的平行四边形是菱形(还可以怎样说?)
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
数学语言
探究活动四:小强同学先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?
猜想:四边都相等的四边形是菱形 。
B
A
C
D
已知:在四边形ABCD中, AB=BC=CD=DA
求证:四边形ABCD是菱形
A
D
C
B
证明:
又∵ AB=BC
∵ AB=CD AD=BC
∴四边形ABCD是平行四边形
∴ ABCD是菱形
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
+邻边相等 =
+对角线线互相垂直=
四条边相等+ =
探究活动五:总结归纳
亲,你能归纳菱形的几种判定方法吗? 它们之间有何异同?
文字语言
图形语言
符号语言
判定法一
判定
法二
对角线互相垂直的平行四边形是菱形
判定法三
四边相等的四边形是菱形
菱形的判定:(自主出题)
)
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
一组邻边相等的平行四边形是菱形
1、如图, ABCD的两条对角线AC、BD
相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.
A
B
C
D
O
∴四边形ABCD是菱形.
∴OA=OC=4
OB=OD=3
证明:
∵ AB=5
∴
∴AC⊥BD
∴ ∠AOB=
又∵ 四边形ABCD是平行四边形
∵ 四边形ABCD是平行四边形
探究活动六:应用新知
(平行四边形的对角线互相平分)
(对角线互相垂直的平行四边形是菱形).
2、已知:如图,AD平分∠BAC,DE∥AC 交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴ □AEDF是菱形
证明:∵DE∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE∥AC
∴∠2=∠3
∵ AD是△ABC的角平分线
∴ ∠1=∠2
∴AE=DE
∴ ∠1=∠3
3、如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
H
G
F
E
D
C
B
A
证明:连接AC、BD
∵四边形ABCD是矩形
∴AC=BD
∵点E、F、G、H为各边中点
∴EF=FG=GH=HE
∴四边形EFGH是菱形
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
二组对边平行或相等
探究活动七: 反思与小结(知识、方法、感想等)
四边形
平行四边形
小丽是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
怎样利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
探究活动八:随堂练习
布置作业
基础题:课本题P98第9、11题
提高题:见下页PPT
1、如下图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于C,EF⊥BC于F,四边形AEFG是菱形吗?
2、已知:如图,□ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
A
B
F
C
D
E
O
∟
∵EF垂直平分AC
∴AO=CO, ∠AOE=90°
∴∠FOC=∠AOE=90°
∵四边形ABCD是平行四边形
∴ AD∥BC ∴AE∥FC
∴∠AEO=∠CFO
∴△AEO≌△CFO
证明:
∴OE=OF
又∵AO=CO
∴四边形AFCE是平行四边形
又∵EF⊥AC
∴四边形AFCE是菱形
谢谢!
聪明的同学们,你能剪出这些美丽的图案吗?
观 察
菱形就在我们身边
学习目标
?? 1、经历菱形的判定方法的探究过程,掌握菱形的三种判定方法??,能根据题目中的条件选择恰当的方法判定四边形是菱形。
?
2、培养学生操作能力和观察、猜想、推理的意识;
体会类比与转化的数学思想。
3、培养合作意识;养成严密的数学逻辑思维习惯.
??
学习重、难点
重点:菱形的判定定理的探究。
难点:菱形的判定定理的探究和应用。
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
边
对角线
角
菱形的定义
菱形的性质
复习意图?
菱形
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。
活动一:温故而知新
活动二
同学们,想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
总结:根据菱形的定义,可得菱形的判定方法一(定义法)
有一组邻边相等的平行四边形叫做菱形
还有其他么方法吗?
ABCD
AB=AD
四边形ABCD是菱形
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可转动的十字架,四周围上一根橡皮筋,做成一个四边形。
(1)任意转动木条,这个四边形总是一个什么图形?你能证明你发现的结论吗?
(2)继续转动木条,观察什么时候橡皮筋围成的四边形变成菱形?
猜想:当木条互相垂直时,这个平行四边形就变成菱形。
合作释疑
∟
探究活动三
命题:对角线互相垂直的平行四边形是菱形.
A
B
C
D
已知:在 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
证明:
∴ ABCD是菱形
又∵ AC ⊥ BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
O
定理:对角线互相垂直的平行四边形是菱形.
判定方法2:
对角线互相垂直的平行四边形是菱形(还可以怎样说?)
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
数学语言
探究活动四:小强同学先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?
猜想:四边都相等的四边形是菱形 。
B
A
C
D
已知:在四边形ABCD中, AB=BC=CD=DA
求证:四边形ABCD是菱形
A
D
C
B
证明:
又∵ AB=BC
∵ AB=CD AD=BC
∴四边形ABCD是平行四边形
∴ ABCD是菱形
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
+邻边相等 =
+对角线线互相垂直=
四条边相等+ =
探究活动五:总结归纳
亲,你能归纳菱形的几种判定方法吗? 它们之间有何异同?
文字语言
图形语言
符号语言
判定法一
判定
法二
对角线互相垂直的平行四边形是菱形
判定法三
四边相等的四边形是菱形
菱形的判定:(自主出题)
)
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
一组邻边相等的平行四边形是菱形
1、如图, ABCD的两条对角线AC、BD
相交于点O,AB= 5 ,AC=8,DB=6
求证:四边形ABCD是菱形.
A
B
C
D
O
∴四边形ABCD是菱形.
∴OA=OC=4
OB=OD=3
证明:
∵ AB=5
∴
∴AC⊥BD
∴ ∠AOB=
又∵ 四边形ABCD是平行四边形
∵ 四边形ABCD是平行四边形
探究活动六:应用新知
(平行四边形的对角线互相平分)
(对角线互相垂直的平行四边形是菱形).
2、已知:如图,AD平分∠BAC,DE∥AC 交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴ □AEDF是菱形
证明:∵DE∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE∥AC
∴∠2=∠3
∵ AD是△ABC的角平分线
∴ ∠1=∠2
∴AE=DE
∴ ∠1=∠3
3、如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
H
G
F
E
D
C
B
A
证明:连接AC、BD
∵四边形ABCD是矩形
∴AC=BD
∵点E、F、G、H为各边中点
∴EF=FG=GH=HE
∴四边形EFGH是菱形
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
二组对边平行或相等
探究活动七: 反思与小结(知识、方法、感想等)
四边形
平行四边形
小丽是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
怎样利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
探究活动八:随堂练习
布置作业
基础题:课本题P98第9、11题
提高题:见下页PPT
1、如下图在△ABC中,∠BAC=90°,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于C,EF⊥BC于F,四边形AEFG是菱形吗?
2、已知:如图,□ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
A
B
F
C
D
E
O
∟
∵EF垂直平分AC
∴AO=CO, ∠AOE=90°
∴∠FOC=∠AOE=90°
∵四边形ABCD是平行四边形
∴ AD∥BC ∴AE∥FC
∴∠AEO=∠CFO
∴△AEO≌△CFO
证明:
∴OE=OF
又∵AO=CO
∴四边形AFCE是平行四边形
又∵EF⊥AC
∴四边形AFCE是菱形
谢谢!
