16.2.3_整数指数幂_课件1
文档属性
| 名称 | 16.2.3_整数指数幂_课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 376.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-20 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
算一算:
第1天,吃到面包的 ;
第2天,吃到面包的 ;即
第3天,吃到面包的 ;即
... ...
第10天,吃到面包的 ;即
第30天,一个月以后,只能吃到面包的 , 即
从前,有一个“聪明的乞丐”,有一次他讨了一块面包。他想,如果我第一天吃这块面包的一半,第二天再吃剩下的一半,……依次每天都吃前一天剩余面包的一半,这样下去,我就永远不用再去讨饭了。你能知道第十天,他将吃到多少面包吗?他的想法对吗?
§16.2.3 整数指数幂(1)
一:本节课的学习目标
1.理解负指数幂的意义
2. 正确熟练地运用整数指数幂性质进行计算。
3. 培养抽象的数学思维能力; 在发展推理能力 和有条理的语言和符号表达能力的同时,进一步体会学习数学的兴趣。
二:重点难点
重点:负整数指数幂的意义及其运算性质.
难点:认识负整数指数幂的产生过程及幂运算法则的扩展过程
回顾:
(n是正整数)
表示的意义是什么?
a
n
探究:
又表示什么样的意义呢?
a
- n
问题1:
做一做, 你发现了什么?
5
5
÷
5
2
(1)
=
5
3
(m,n是正整数,且m>n)
填空:
5
7
2
5-7
-2
(2)
则有:
这就是说:a-n(a≠0)是an 的倒数
属于分式
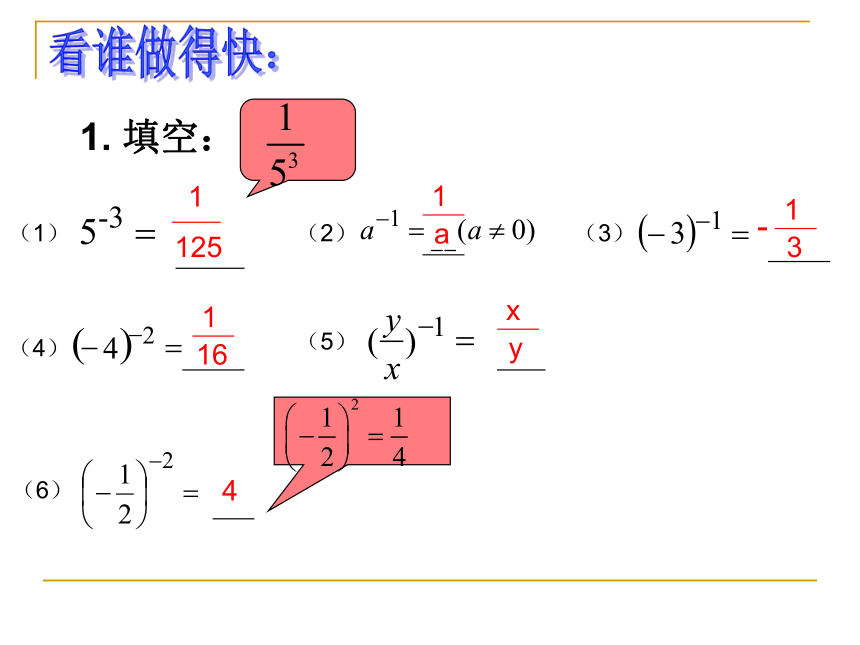
1. 填空:
1
a
(2)
1
3
-
(3)
1
16
(6)
4
x
y
(1)
1
125
(5)
=
-
1
)
(
x
y
(4)
(
)
=
-
-
2
4
下列等式是否正确?为什么?
(1)
(2)
解:
(1)
(2)
负指数幂的引入可以使除法转化为幂的乘法,即
正整数指数幂的性质 (m,n是正整数)
当a≠0时,
问题2:当幂的指数为负数或者零时,
有什么样的运算性质呢?
( 1 )
( 2 )
( 3 )
( 4 )
( 5 )
=
a
8
3+5
a
3
a
5
.
a
=
5
3
a
a
.
=
算一算:
口 答:
=
即:
=
即:
类似于前面的讨论,同学们可以进一步用负整数指数幂或0指数幂,对于前面提到的正整数指数幂的运算性质进行试验,看看这些这些性质是否还适用
分组讨论:
第一组:
第二组:
第三组:
由大家前面的讨论可知:整数指数幂的所有运算性质用于指数是负数和零的幂的运算也是完全成立的
整数指数幂的性质:
(注意:m , n 是 整 数 )
一.(课本P20 ) 例9 计算:
解:(1)
(2)
(2)
(1)
(1)
(2)
二 课堂达标练习 计算
解:原式
解:原式
综合运用幂的运算法则进行计算,先做乘方,再做乘除,最后做加减,若遇括号,应做括号内的运算,最后的结果保留正整数指数幂的形式.
负整数指数幂的意义
整数指数幂的运算性质
由例10可知,利用负整数指数幂的意义能把幂的乘除运算互相转化
提升能力
1.已知5x-3y+2=0,求105x÷103y的值
【提示】 先根据已知条件求出m和n的值
,求(1+x2)m+n÷(1+x2)3n的值
2. ,
【提示】 5x-3y=-2 ,
即
即
=
即:
=
即:
即
即
算一算:
第1天,吃到面包的 ;
第2天,吃到面包的 ;即
第3天,吃到面包的 ;即
... ...
第10天,吃到面包的 ;即
第30天,一个月以后,只能吃到面包的 , 即
从前,有一个“聪明的乞丐”,有一次他讨了一块面包。他想,如果我第一天吃这块面包的一半,第二天再吃剩下的一半,……依次每天都吃前一天剩余面包的一半,这样下去,我就永远不用再去讨饭了。你能知道第十天,他将吃到多少面包吗?他的想法对吗?
§16.2.3 整数指数幂(1)
一:本节课的学习目标
1.理解负指数幂的意义
2. 正确熟练地运用整数指数幂性质进行计算。
3. 培养抽象的数学思维能力; 在发展推理能力 和有条理的语言和符号表达能力的同时,进一步体会学习数学的兴趣。
二:重点难点
重点:负整数指数幂的意义及其运算性质.
难点:认识负整数指数幂的产生过程及幂运算法则的扩展过程
回顾:
(n是正整数)
表示的意义是什么?
a
n
探究:
又表示什么样的意义呢?
a
- n
问题1:
做一做, 你发现了什么?
5
5
÷
5
2
(1)
=
5
3
(m,n是正整数,且m>n)
填空:
5
7
2
5-7
-2
(2)
则有:
这就是说:a-n(a≠0)是an 的倒数
属于分式
1. 填空:
1
a
(2)
1
3
-
(3)
1
16
(6)
4
x
y
(1)
1
125
(5)
=
-
1
)
(
x
y
(4)
(
)
=
-
-
2
4
下列等式是否正确?为什么?
(1)
(2)
解:
(1)
(2)
负指数幂的引入可以使除法转化为幂的乘法,即
正整数指数幂的性质 (m,n是正整数)
当a≠0时,
问题2:当幂的指数为负数或者零时,
有什么样的运算性质呢?
( 1 )
( 2 )
( 3 )
( 4 )
( 5 )
=
a
8
3+5
a
3
a
5
.
a
=
5
3
a
a
.
=
算一算:
口 答:
=
即:
=
即:
类似于前面的讨论,同学们可以进一步用负整数指数幂或0指数幂,对于前面提到的正整数指数幂的运算性质进行试验,看看这些这些性质是否还适用
分组讨论:
第一组:
第二组:
第三组:
由大家前面的讨论可知:整数指数幂的所有运算性质用于指数是负数和零的幂的运算也是完全成立的
整数指数幂的性质:
(注意:m , n 是 整 数 )
一.(课本P20 ) 例9 计算:
解:(1)
(2)
(2)
(1)
(1)
(2)
二 课堂达标练习 计算
解:原式
解:原式
综合运用幂的运算法则进行计算,先做乘方,再做乘除,最后做加减,若遇括号,应做括号内的运算,最后的结果保留正整数指数幂的形式.
负整数指数幂的意义
整数指数幂的运算性质
由例10可知,利用负整数指数幂的意义能把幂的乘除运算互相转化
提升能力
1.已知5x-3y+2=0,求105x÷103y的值
【提示】 先根据已知条件求出m和n的值
,求(1+x2)m+n÷(1+x2)3n的值
2. ,
【提示】 5x-3y=-2 ,
即
即
=
即:
=
即:
即
即
