16.3分式方程的应用(第2课时)
文档属性
| 名称 | 16.3分式方程的应用(第2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1016.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-20 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
16.3 分式方程
与实际问题
填空 解分式方程的一般步骤是:
在方程的两边都乘以最简公分母,化成____________方程;
解这个____________方程;
检验:把__________方程的根代入____________.如果值_________,就是原方程的根;如果值__________,就是增根.应当__________,原分式方程无解;
写出分式方程的解.
整式
整式
这个整式
最简公分母中
不为零
为零
舍去
知识回顾:
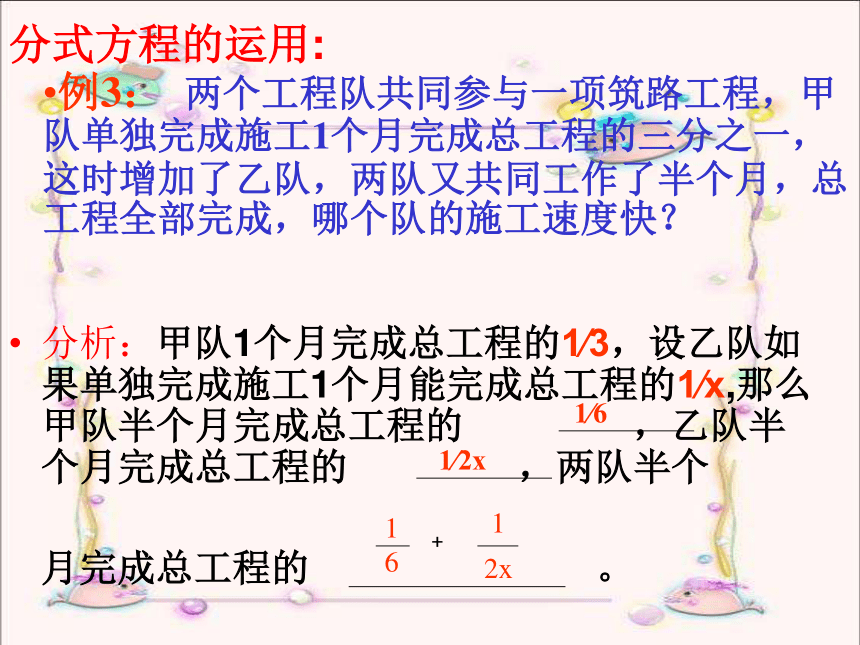
分式方程的运用:
分析:甲队1个月完成总工程的1∕3,设乙队如果单独完成施工1个月能完成总工程的1∕x,那么甲队半个月完成总工程的 ,乙队半个月完成总工程的 ,两队半个
月完成总工程的 。
1∕6
1∕2x
1
6
﹢
1
2x
例3: 两个工程队共同参与一项筑路工程,甲队单独完成施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
列方程的关键是什么?问题中的那个等量关系可以用来列方程?
关键:找出相等关系
甲队施工1个月的工作量+甲乙共施工半个月的工作量=总工作量
解:设乙队如果单独施工1个月能完成总工程的 。
由题意得:
1
x
1
3
+
1
6
+
1
2x
=
1
2x+x+3=6x
x=1
经检验:x=1是原分式方程的解,且符合题意。
∵ 1﹥
1
3
∴ 乙队施工速度快。
分析:这里的字母v、s表示已知数据,设提速前列车的平均速度为x千米∕小时,先考虑下面的空:
从2004年5月起某列车平均提速v千米∕小时,用相
同的时间,列车提速前行驶s千米,提速后比提速
前多行驶50千米,提速前列车的平均速度为多少?
例4:
提速前列车行驶 千米所用的时间为 小时,
提速后列车的平均速度为 千米∕小时,
提速后列车运行 千米所用的时间为
小时。
(x+v)
s
(s+50)
根据行驶时间的等量关系,得:
解:设提速前这次列车的平均速度为x千米∕小时,
则提速前它行驶s千米所用的时间为s/x小时,提速后
列车的平均速度为(x+v)千米∕小时,提速后它
运行(s+50)千米所用的时间为 小时。
方程两边同乘以x(x+v),得:
s(x+v)=x(s+50)
解得:
检验:由于v,s都是正数, 时x(x+v)≠0,
是原方程的解。
答:提速前列车的平均速度为 千米/小时
x千米∕小时
s千米
(x+v)千米∕小时
(s+50)
总结:列分式方程解应用题的方法和步骤如下:
问题:请分析列分式方程解应用题与以前学习的列方程解应用题有什么区别?
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出方程.
4.解:认真仔细解这个分式方程.
5.验:检验.(是否是分式方程的根, 是否符合题意)
6.答:注意单位和语言完整.
区别:解方程后要检验。
补充: 甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?
解:设甲每小时做x个零件则乙每小时做( x -6)个零件,
依题意得:
经检验X=18是原方程的根,且符合题意。
答:甲每小时做18个,乙每小时12个
请审题分析 题意设元
我们所列的是一个分式方程,这是分式方程的应用
由x=18得x-6=12
等量关系:甲用时间=乙用时间
甲、乙两种商品,已知甲的价格每件比乙多6元,买甲90件所用的钱和买乙60件所用钱相等,求甲、乙每件商品的价格各多少元?
试一试
练习1:某农场开挖一条长960米的渠道,开工后工作效率比计划提高50%,结果提前4天完成任务。原计划每天挖多少米?
解:设原计划每天挖x米,则实际每天挖 _________ __ 米。
x(1+50%)
工作效率比计划提高50%
每天比计划多挖50%
练习2:甲、乙二人同时从张庄出发,步行15千米到李庄。甲比乙每小时多走1千米,结果比乙早到半小时。二人每小时各走多少千米?
解:设甲速度为x千米/时,则乙速度为________千米/时
(x-1)
小结:
1、列分式方程解应用题,应该注意解题的六个步骤。
2、列方程的关键是要准确设元(可直接设,也可间接设)的前提下找出等量关系。
3、解题过程注意画图或列表帮助分析题意找等量关系。
4、注意不要漏检验和写答案。
再 见!
16.3 分式方程
与实际问题
填空 解分式方程的一般步骤是:
在方程的两边都乘以最简公分母,化成____________方程;
解这个____________方程;
检验:把__________方程的根代入____________.如果值_________,就是原方程的根;如果值__________,就是增根.应当__________,原分式方程无解;
写出分式方程的解.
整式
整式
这个整式
最简公分母中
不为零
为零
舍去
知识回顾:
分式方程的运用:
分析:甲队1个月完成总工程的1∕3,设乙队如果单独完成施工1个月能完成总工程的1∕x,那么甲队半个月完成总工程的 ,乙队半个月完成总工程的 ,两队半个
月完成总工程的 。
1∕6
1∕2x
1
6
﹢
1
2x
例3: 两个工程队共同参与一项筑路工程,甲队单独完成施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
列方程的关键是什么?问题中的那个等量关系可以用来列方程?
关键:找出相等关系
甲队施工1个月的工作量+甲乙共施工半个月的工作量=总工作量
解:设乙队如果单独施工1个月能完成总工程的 。
由题意得:
1
x
1
3
+
1
6
+
1
2x
=
1
2x+x+3=6x
x=1
经检验:x=1是原分式方程的解,且符合题意。
∵ 1﹥
1
3
∴ 乙队施工速度快。
分析:这里的字母v、s表示已知数据,设提速前列车的平均速度为x千米∕小时,先考虑下面的空:
从2004年5月起某列车平均提速v千米∕小时,用相
同的时间,列车提速前行驶s千米,提速后比提速
前多行驶50千米,提速前列车的平均速度为多少?
例4:
提速前列车行驶 千米所用的时间为 小时,
提速后列车的平均速度为 千米∕小时,
提速后列车运行 千米所用的时间为
小时。
(x+v)
s
(s+50)
根据行驶时间的等量关系,得:
解:设提速前这次列车的平均速度为x千米∕小时,
则提速前它行驶s千米所用的时间为s/x小时,提速后
列车的平均速度为(x+v)千米∕小时,提速后它
运行(s+50)千米所用的时间为 小时。
方程两边同乘以x(x+v),得:
s(x+v)=x(s+50)
解得:
检验:由于v,s都是正数, 时x(x+v)≠0,
是原方程的解。
答:提速前列车的平均速度为 千米/小时
x千米∕小时
s千米
(x+v)千米∕小时
(s+50)
总结:列分式方程解应用题的方法和步骤如下:
问题:请分析列分式方程解应用题与以前学习的列方程解应用题有什么区别?
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出方程.
4.解:认真仔细解这个分式方程.
5.验:检验.(是否是分式方程的根, 是否符合题意)
6.答:注意单位和语言完整.
区别:解方程后要检验。
补充: 甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?
解:设甲每小时做x个零件则乙每小时做( x -6)个零件,
依题意得:
经检验X=18是原方程的根,且符合题意。
答:甲每小时做18个,乙每小时12个
请审题分析 题意设元
我们所列的是一个分式方程,这是分式方程的应用
由x=18得x-6=12
等量关系:甲用时间=乙用时间
甲、乙两种商品,已知甲的价格每件比乙多6元,买甲90件所用的钱和买乙60件所用钱相等,求甲、乙每件商品的价格各多少元?
试一试
练习1:某农场开挖一条长960米的渠道,开工后工作效率比计划提高50%,结果提前4天完成任务。原计划每天挖多少米?
解:设原计划每天挖x米,则实际每天挖 _________ __ 米。
x(1+50%)
工作效率比计划提高50%
每天比计划多挖50%
练习2:甲、乙二人同时从张庄出发,步行15千米到李庄。甲比乙每小时多走1千米,结果比乙早到半小时。二人每小时各走多少千米?
解:设甲速度为x千米/时,则乙速度为________千米/时
(x-1)
小结:
1、列分式方程解应用题,应该注意解题的六个步骤。
2、列方程的关键是要准确设元(可直接设,也可间接设)的前提下找出等量关系。
3、解题过程注意画图或列表帮助分析题意找等量关系。
4、注意不要漏检验和写答案。
再 见!
