18.1.2 勾股定理(2)
文档属性
| 名称 | 18.1.2 勾股定理(2) |  | |
| 格式 | zip | ||
| 文件大小 | 152.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-20 11:53:36 | ||
图片预览




文档简介
(共14张PPT)
a
b
c
c2=a2 + b2
结论变形
知识&回顾
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
a2=c2 - b2
b2=c2 -a2
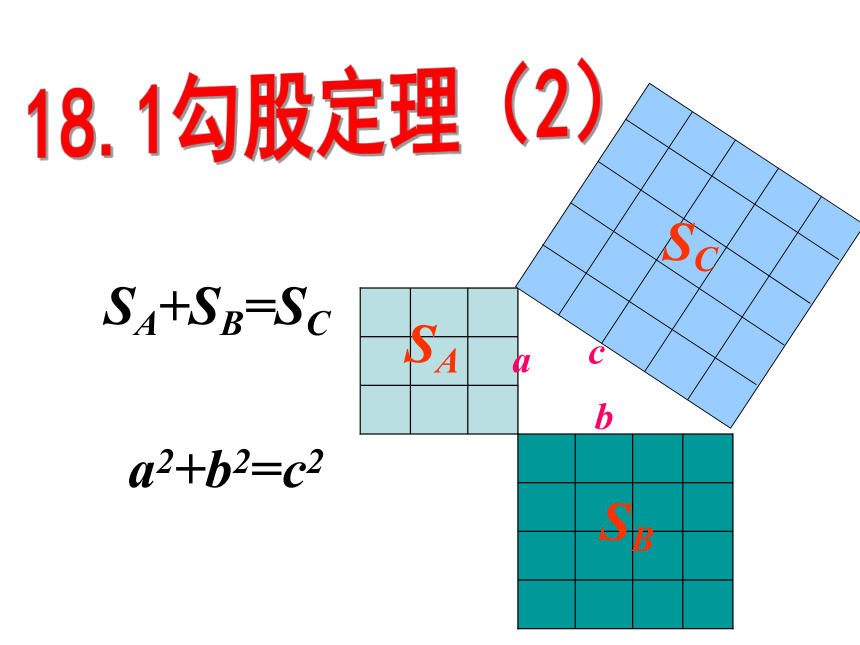
SA+SB=SC
a2+b2=c2
a
b
c
SA
SB
SC
学习目标:
学会将实际问题转化为直角三角形的数学模型,利用勾股定理解决简单的实际问题。
自学指导一:
阅读课本67页探究2,
要求:填写课本中的空
A
C
O
B
D
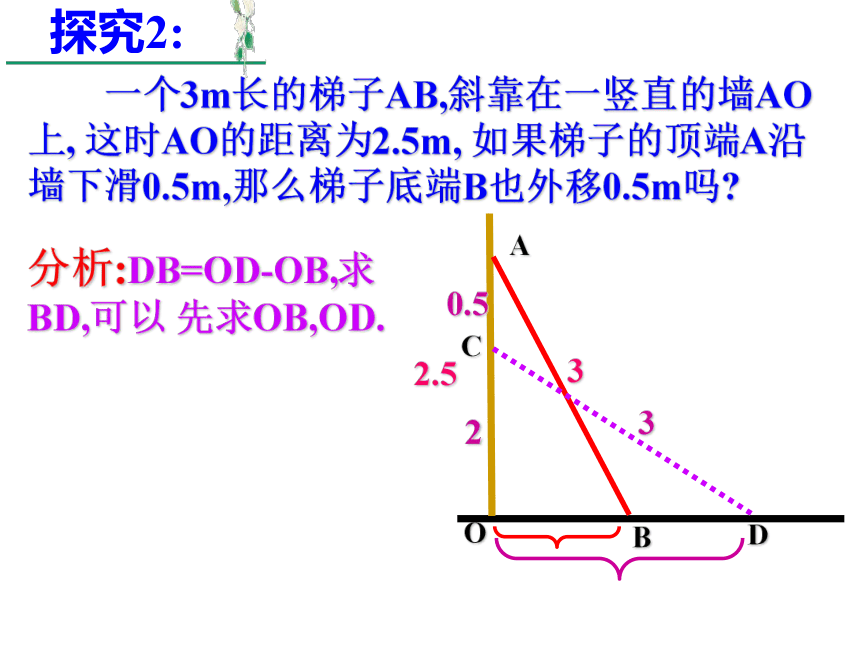
一个3m长的梯子AB,斜靠在一竖直的墙AO上, 这时AO的距离为2.5m, 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
探究2:
3
2.5
0.5
2
3
分析:DB=OD-OB,求BD,可以 先求OB,OD.
A
C
O
B
D
梯子的顶端沿墙下滑0.5m,梯子底端外移_______.
在Rt△AOB中,
在Rt△COD中,
OD-OB = 2.236 -1.658 ≈0.58
0.58 m
一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
3
2.5
2
3
1.658
2.236
探究2:
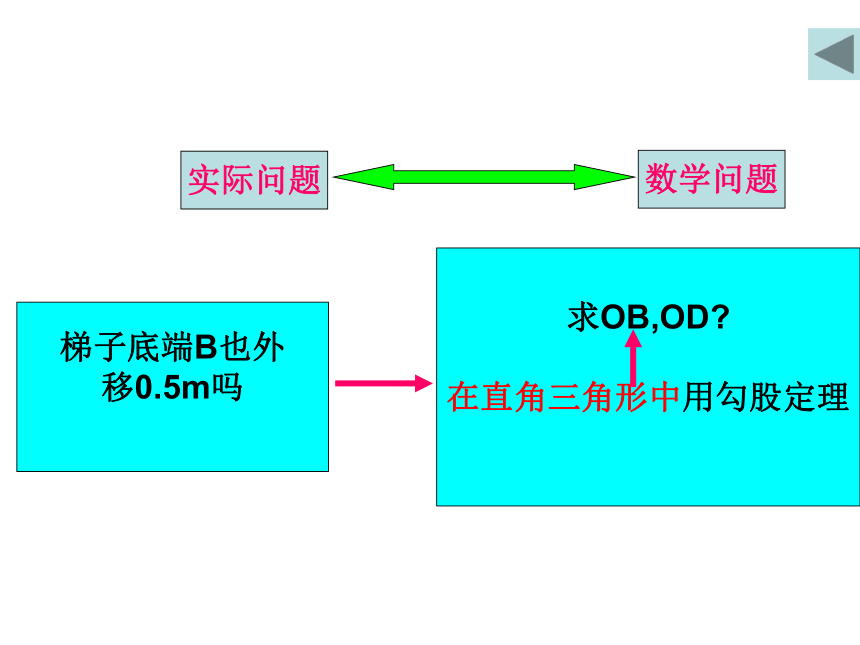
实际问题
数学问题
梯子底端B也外
移0.5m吗
求OB,OD
在直角三角形中用勾股定理
课后练习1、2题
当堂训练 :
2、在等腰△ABC中,AB=AC=88mm,BC=64mm,求△ABC的面积和AC边上的高.
两个直角三角形中,如果有一条公共边,可利用勾股定理建立方程求解.
D
A
B
C
E
《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?
X
2
5
2
(X+1)
2
+
=
X
X+1
5
1
方程思想:利用直角三角形中三边等量关系,可建立方程求解.
(2)运用勾股定理解决生活中的一 些实际问题.
(1)将实际问题转化为数学问题, 建立数学模型.
小结
直角三角形ABC的面积为20cm2 ,在AB的同侧分别以AB、BC、CA为直径做三个半圆,求阴影部分的面积。
A
C
B
如图,∠C=90°,图中有阴影的三个半圆的面积有什么关系?
A
C
B
S3
S1
S2
作业
课本P70 习题18.1第4、5、8题
a
b
c
c2=a2 + b2
结论变形
知识&回顾
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
a2=c2 - b2
b2=c2 -a2
SA+SB=SC
a2+b2=c2
a
b
c
SA
SB
SC
学习目标:
学会将实际问题转化为直角三角形的数学模型,利用勾股定理解决简单的实际问题。
自学指导一:
阅读课本67页探究2,
要求:填写课本中的空
A
C
O
B
D
一个3m长的梯子AB,斜靠在一竖直的墙AO上, 这时AO的距离为2.5m, 如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
探究2:
3
2.5
0.5
2
3
分析:DB=OD-OB,求BD,可以 先求OB,OD.
A
C
O
B
D
梯子的顶端沿墙下滑0.5m,梯子底端外移_______.
在Rt△AOB中,
在Rt△COD中,
OD-OB = 2.236 -1.658 ≈0.58
0.58 m
一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗
3
2.5
2
3
1.658
2.236
探究2:
实际问题
数学问题
梯子底端B也外
移0.5m吗
求OB,OD
在直角三角形中用勾股定理
课后练习1、2题
当堂训练 :
2、在等腰△ABC中,AB=AC=88mm,BC=64mm,求△ABC的面积和AC边上的高.
两个直角三角形中,如果有一条公共边,可利用勾股定理建立方程求解.
D
A
B
C
E
《九章算术》:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,请问这个水的深度与这根芦苇的长度各是多少?
X
2
5
2
(X+1)
2
+
=
X
X+1
5
1
方程思想:利用直角三角形中三边等量关系,可建立方程求解.
(2)运用勾股定理解决生活中的一 些实际问题.
(1)将实际问题转化为数学问题, 建立数学模型.
小结
直角三角形ABC的面积为20cm2 ,在AB的同侧分别以AB、BC、CA为直径做三个半圆,求阴影部分的面积。
A
C
B
如图,∠C=90°,图中有阴影的三个半圆的面积有什么关系?
A
C
B
S3
S1
S2
作业
课本P70 习题18.1第4、5、8题
