9.3 一元一次不等式组 课件(共21张PPT)
文档属性
| 名称 | 9.3 一元一次不等式组 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 00:00:00 | ||
图片预览






文档简介
9.3 一元一次不等式组
2021年春人教版七年级(下)数学
第九章 不等式与不等式组
问题:用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200吨而不足1500吨,那么大约需要多少时间才能将污水抽完?
解:设Xmin将污水抽完,则x同时满足不等式
30X>1200
30X<1500
新课导入
30X>1200
30X<1500
由几个含有相同未知数的一元一次不等式 组成的不等式组叫做一元一次不等式组
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量至少是两个或者多个。
探究新知
①
②
由不等式②,解得 x<50
30x>1200
30x<1500
由不等式①,解得 x>40
思考:怎样解不等式组
探究新知
类似于方程组,不等式组的解集是组成它的各不等式解集的公共部分.
-10 0 10 20 30 40 50 60
在同一数轴上分别表示出不等式① 、②的解集.
求不等式组的解集的过程叫做解不等式组.
探究新知
-2 -1 0 1 2 3 4 5 6
从上图可以找出两个不等式解集的公共部分,得不等式组的解集是: ___________
不等式 的解集是:___________
不等式 的解集是:___________
①
②
猜猜看,不等式组
的解集是什么?
在数轴上表示不等式的解集时应注意:大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.
不等式组的解集:各个不等式的解集的公共部分.
探究新知
–2 –1 0 1 2
–2 –1 0 1 2
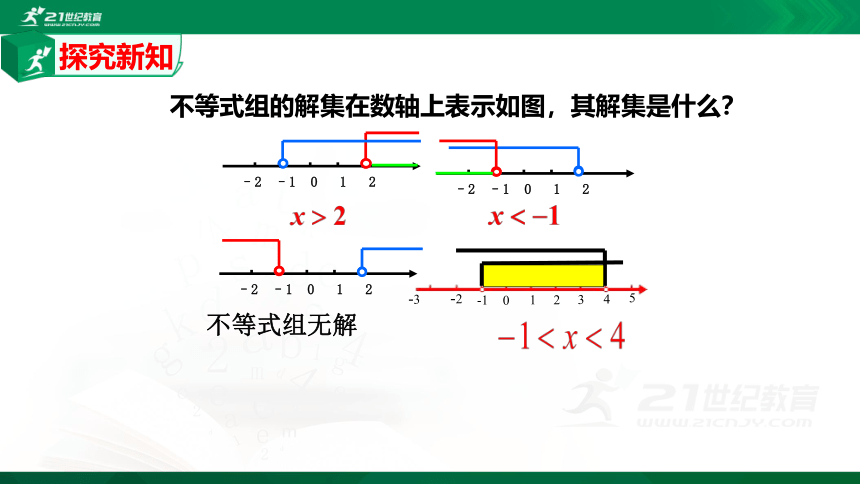
不等式组的解集在数轴上表示如图,其解集是什么?
不等式组无解
–2 –1 0 1 2
-3
-2
-1
0
4
2
1
3
5
探究新知
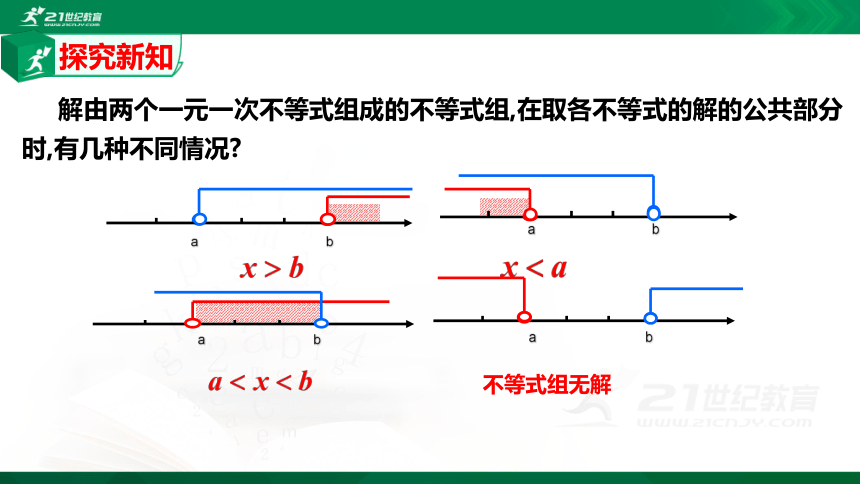
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
不等式组无解
a b
a b
探究新知
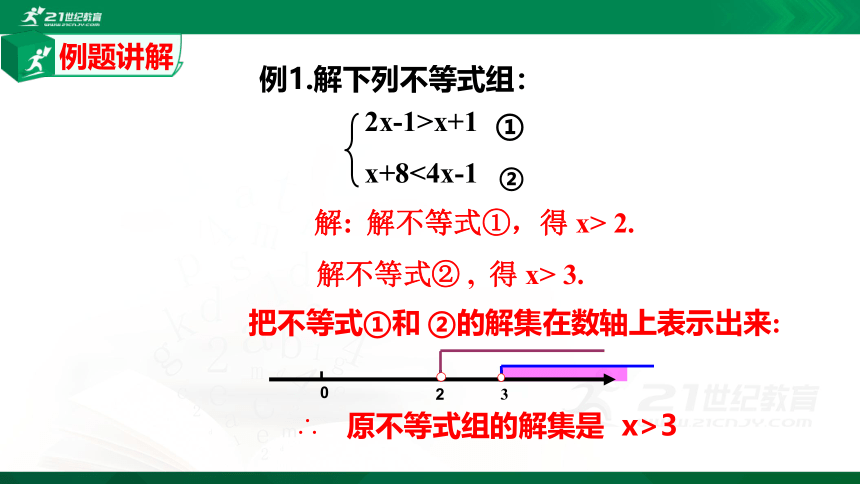
例1.解下列不等式组:
①
②
解: 解不等式①,得 x> 2.
解不等式② , 得 x> 3.
∴ 原不等式组的解集是 x>3
把不等式①和 ②的解集在数轴上表示出来:
2
3
0
2x-1>x+1
x+8<4x-1
例题讲解
解一元一次不等式组的一般步骤:
分别求出各个不等式的解集
在数轴上表示出各个不等式的解集
找公共部分
用不等式表示出解集
归纳小结
因此,原不等式组无解 。
解:解不等式①,得
解不等式②,得
0
8
①
②
例2.解不等式组
例题讲解
(不是)
(是)
(不是)
(是)
(是)
1.下列式子,哪些是一元一次不等式组?
课堂练习
2.选择题:
(1)不等式组 的解集是( )
A.x ≥2,
D.x =2.
B.x≤2,
C. 无解,
(2)不等式组 的整数解是( )
≤1
D. x≤1.
A. 0, 1 ,
B. 0 ,
C. 1,
D
C
≥2
≤2
课堂练习
D.不能确定.
A. -2, 0, -1 ,
B. -2
C. -2, -1,
(3)不等式组 的负整数解是( )
≥ -2,
(4)不等式组 的解集在数轴上表示为( )
≥-2,
A.
D.
C.
B.
C
B
-5
-2
-5
-2
-5
-2
-5
-2
课堂练习
(5)不等式组 的解集在数轴上可表示为 ( )
B
课堂练习
3解下列不等式组:
(1) x-1<3x ① (2) x-1>3 ①
X+1>3 ② x+1<3-4x ②
解:(1)由①得X>-0.5
由②得X>2
解:(2)由①得 X>4
由②得X<0.4
0
0
0.5
1
0.4
4
o
o
o
o
不等式组的解集为x>2
不等式无解
课堂练习
2x>1-x
x+2<4x-1
{
(1)
x-5>1+2x
3x+2<4x
{
(2)
4.解下列不等式组
解(1) 由①得 3x >1
①
②
②
①
1
3
x >
由② 得 3x> 3
x> 1
所以原不等式组的解集是x>1
(2) 由①得 x <-6
由② 得 x> 2
所以原不等式组无解.
课堂练习
2
3
(3)
x +5 >1 - x
x -1< x -
3
4
1
8
(3)解: 由①得 2x+15 >3-3x
①
②
由② 得 8x-8<6x-1
x<3.5
所以原不等式组的解集是 -2.4 < x <3.5
5x> -12
x>-2.4
课堂练习
1. 由几个一元一次不等式所组成的不等式组叫做一 元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(一)概念
(找不到公共部分则不等式组无解)
利用规律:
同大取大,同小取小;
大小小大中间找,大大小小解不了。
课堂小结
再见
2021年春人教版七年级(下)数学
第九章 不等式与不等式组
问题:用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200吨而不足1500吨,那么大约需要多少时间才能将污水抽完?
解:设Xmin将污水抽完,则x同时满足不等式
30X>1200
30X<1500
新课导入
30X>1200
30X<1500
由几个含有相同未知数的一元一次不等式 组成的不等式组叫做一元一次不等式组
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量至少是两个或者多个。
探究新知
①
②
由不等式②,解得 x<50
30x>1200
30x<1500
由不等式①,解得 x>40
思考:怎样解不等式组
探究新知
类似于方程组,不等式组的解集是组成它的各不等式解集的公共部分.
-10 0 10 20 30 40 50 60
在同一数轴上分别表示出不等式① 、②的解集.
求不等式组的解集的过程叫做解不等式组.
探究新知
-2 -1 0 1 2 3 4 5 6
从上图可以找出两个不等式解集的公共部分,得不等式组的解集是: ___________
不等式 的解集是:___________
不等式 的解集是:___________
①
②
猜猜看,不等式组
的解集是什么?
在数轴上表示不等式的解集时应注意:大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.
不等式组的解集:各个不等式的解集的公共部分.
探究新知
–2 –1 0 1 2
–2 –1 0 1 2
不等式组的解集在数轴上表示如图,其解集是什么?
不等式组无解
–2 –1 0 1 2
-3
-2
-1
0
4
2
1
3
5
探究新知
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况?
a b
a b
不等式组无解
a b
a b
探究新知
例1.解下列不等式组:
①
②
解: 解不等式①,得 x> 2.
解不等式② , 得 x> 3.
∴ 原不等式组的解集是 x>3
把不等式①和 ②的解集在数轴上表示出来:
2
3
0
2x-1>x+1
x+8<4x-1
例题讲解
解一元一次不等式组的一般步骤:
分别求出各个不等式的解集
在数轴上表示出各个不等式的解集
找公共部分
用不等式表示出解集
归纳小结
因此,原不等式组无解 。
解:解不等式①,得
解不等式②,得
0
8
①
②
例2.解不等式组
例题讲解
(不是)
(是)
(不是)
(是)
(是)
1.下列式子,哪些是一元一次不等式组?
课堂练习
2.选择题:
(1)不等式组 的解集是( )
A.x ≥2,
D.x =2.
B.x≤2,
C. 无解,
(2)不等式组 的整数解是( )
≤1
D. x≤1.
A. 0, 1 ,
B. 0 ,
C. 1,
D
C
≥2
≤2
课堂练习
D.不能确定.
A. -2, 0, -1 ,
B. -2
C. -2, -1,
(3)不等式组 的负整数解是( )
≥ -2,
(4)不等式组 的解集在数轴上表示为( )
≥-2,
A.
D.
C.
B.
C
B
-5
-2
-5
-2
-5
-2
-5
-2
课堂练习
(5)不等式组 的解集在数轴上可表示为 ( )
B
课堂练习
3解下列不等式组:
(1) x-1<3x ① (2) x-1>3 ①
X+1>3 ② x+1<3-4x ②
解:(1)由①得X>-0.5
由②得X>2
解:(2)由①得 X>4
由②得X<0.4
0
0
0.5
1
0.4
4
o
o
o
o
不等式组的解集为x>2
不等式无解
课堂练习
2x>1-x
x+2<4x-1
{
(1)
x-5>1+2x
3x+2<4x
{
(2)
4.解下列不等式组
解(1) 由①得 3x >1
①
②
②
①
1
3
x >
由② 得 3x> 3
x> 1
所以原不等式组的解集是x>1
(2) 由①得 x <-6
由② 得 x> 2
所以原不等式组无解.
课堂练习
2
3
(3)
x +5 >1 - x
x -1< x -
3
4
1
8
(3)解: 由①得 2x+15 >3-3x
①
②
由② 得 8x-8<6x-1
x<3.5
所以原不等式组的解集是 -2.4 < x <3.5
5x> -12
x>-2.4
课堂练习
1. 由几个一元一次不等式所组成的不等式组叫做一 元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(一)概念
(找不到公共部分则不等式组无解)
利用规律:
同大取大,同小取小;
大小小大中间找,大大小小解不了。
课堂小结
再见
