河南省镇平一高2012年春期高三第二次周考(数学文)
文档属性
| 名称 | 河南省镇平一高2012年春期高三第二次周考(数学文) |

|
|
| 格式 | zip | ||
| 文件大小 | 361.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-20 00:00:00 | ||
图片预览



文档简介
2012年春高三第二次周考(2月18日)
数 学(文)试题
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的,请用2B铅笔把答题卡上对应题目的答案标号涂黑.
1.已知集合,若,则等于
( )
A. B. C.或 D.或
2、已知 ( )
A. 6 B. 8 C. 10 D.
3.在下列四个命题中,其中为真命题的是 ( )
A. 命题“若,则”的逆否命题是“若,则”
B. 若命题:所有幂函数的图像不过第四象限,命题:所有抛物线的离心率为1,则命题且为真
C. 若命题p:,则
D. 若,则
4.若=-,则cosα+sinα的值为
A.- B.- C. D.
5.设,,则双曲线的离心率的概率是( )
A. B. C. D.
6.函数具有性质( )
A.最大值为,图象关于直线对称
B.最大值为1,图象关于直线对称
C.最大值为,图象关于点对称
D.最大值为1,图象关于点对称
7. 某程序框图如图所示,该程序运行后,输出的值为31,则等于( )
A. B.
C. D.
(第7题图)
8. 椭圆与直线交于、两点,过原点与线段中点的直线的斜率为,则的值为( )
A. B. C. HYPERLINK "http://www./" EMBED Equation.DSMT4 D.
9.若函数的导函数,则使得函数单调递减的一个充分不必要条件是∈( )
10.已知满足,则的最小值是( )
A.0 B. C. D.2
11.已知中,,点为边所在直线上的一个动点,则满足( )
A.最大值为16 B.最小值为4 C.为定值 D.与的位置有关
12.设函数是定义在上的奇函数,且当时,单调递减,若数列是等差数列,且,则的值
( )
A.恒为正数 B.恒为负数 C.恒为0 D.可正可负
第II卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13.若等差数列{}的首项为a1,公差为d,前n项的和为,则数列{}为等差数列,且通项为=a1+(n-1).类似地,请完成下列命题:若各项均为正数的等比数列{}的首项为b1,公比为q,前n项的积为,则数列________为等比数列且通项为_____________.
14. 一个几何体的三视图及其尺寸(单位:cm) ,如图所示,则该几何体的侧面积为 cm.
15. 已知椭圆的左、右焦点分别为,若椭圆上存在点(异于长轴的端点),使得,则该椭圆离心率的取值范围是 .
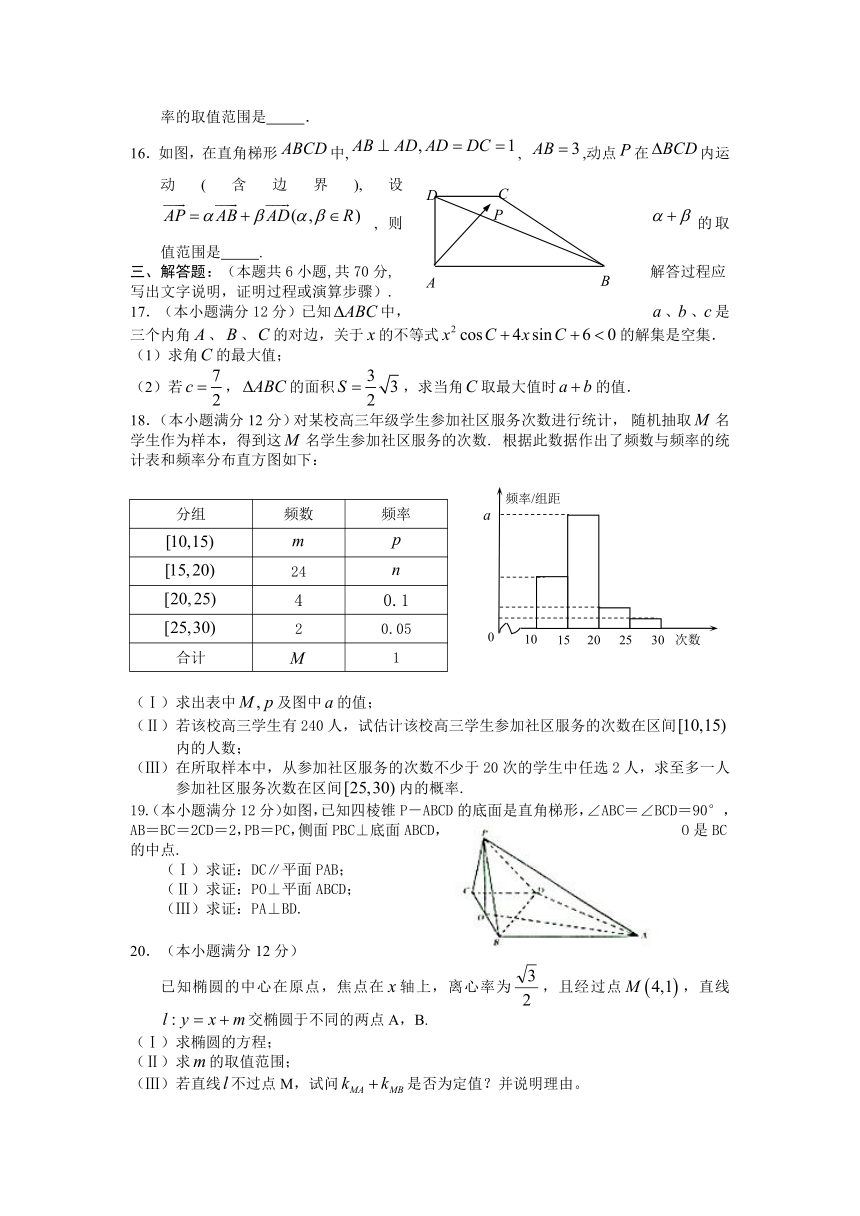
16.如图,在直角梯形中,, ,动点在内运动(含边界),设,则的取值范围是 .
三、解答题:(本题共6小题,共70分,解答过程应写出文字说明,证明过程或演算步骤).
17.(本小题满分12分)已知中,、、是三个内角、、的对边,关于的不等式的解集是空集.
(1)求角的最大值;
(2)若,的面积,求当角取最大值时的值.
18 ( ).(本小题满分12分)对某校高三年级学生参加社区服务次数进行统计, 随机抽取名学生作为样本,得到这名学生参加社区服务的次数. 根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 频数 频率
24
4 0.1
2 0.05
合计 1
(Ⅰ)求出表中及图中的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间 内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间内的概率.
19.(本小题满分12分)如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
(Ⅰ)求证:DC∥平面PAB;
(Ⅱ)求证:PO⊥平面ABCD;
(Ⅲ)求证:PA⊥BD.
20.(本小题满分12分)
已知椭圆的中心在原点,焦点在轴上,离心率为 ( http: / / www. ),且经过点,直线 ( http: / / www. )交椭圆于不同的两点A,B.
(Ⅰ)求椭圆的方程;
(Ⅱ)求的取值范围;
(Ⅲ)若直线 ( http: / / www. )不过点M,试问是否为定值?并说明理由。
21.(本小题满分12分)已知函数f(x)= HYPERLINK "http://www./" EMBED Equation.DSMT4 在点(-l ,f(-1))的切线方程为x+y+3=0.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)=lnx,求证:g(x)≥f(x)在x∈[1,+∞)上恒成立;
(Ⅲ)已知0<a<b,求证:>.
请考生在第(22)、(23)两题中任选一题做答,如果多做,则按所做的第一题记分。
22.(本小题满分10分)选修4-1:几何证明选讲
已知ABC中,AB=AC, D是 ABC外接圆劣弧AC弧上的点(不与点A,C重合),延长BD至E。
(1)求证:AD的延长线平分CDE;
(2)若BAC=30°,ABC中BC边上的高为2+,求ABC外接圆的面积。
23.(本小题满分10分)选修4-5:不等式选讲
设函数 ( http: / / www. / )
(1)求函数的值域;
(2)若,求成立时的取值范围。
2012年春期高三第二次周考
文科数学参考答案
1—5 DCBCA 6-10 CCACB 11-12 C A
13. || ;=b1() n-1 14. 80
15. 16.
17.解:(1)显然 不合题意,则有,---------------------2分
即, 即, 故,--4分
∴角的最大值为。……………………------------------------------------6分
(2)当=时,,∴-------8分
由余弦定理得,
∴,∴。……………12分
18.解(Ⅰ)由分组内的频数是4,频率是0.1知,,所以
因为频数之和为,所以,. -----4分
因为是对应分组的频率与组距的商,所以------6分
(Ⅱ)因为该校高三学生有240人,分组内的频率是,
所以估计该校高三学生参加社区服务的次数在此区间内的人数为人. ……8分
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有人,
设在区间内的人为,在区间内的人为.
则任选人共有
,15种情况, ……10分
而两人都在内只能是一种,所以所求概率为-12分
20.(Ⅰ),----------------------------------------------------2分
依题意设椭圆方程为: HYPERLINK "http://www." 把点代入,得 HYPERLINK "http://www."
椭圆方程为 HYPERLINK "http://www." ----------------------------------------------------------4分
(Ⅱ)把代入椭圆方程得: HYPERLINK "http://www." ,
由△可得 HYPERLINK "http://www." -----------------------------------------------------6分
(Ⅲ)设,A,B与M不重合,
HYPERLINK "http://www." ,--------------------------------------------------8分
HYPERLINK "http://www." EMBED Equation.DSMT4 ,
HYPERLINK "http://www." EMBED Equation.DSMT4 为定值0.---- --------------12分
21.解:
22.解:(Ⅰ)如图,设F为AD延长线上一点,∵A,B,C,D四点共圆,
∴∠CDF=∠ABC, 又AB=AC ∴∠ABC=∠ACB,且∠ADB=∠ACB, ∴∠ADB=∠CDF,对顶角∠EDF=∠ADB, 故∠EDF=∠CDF,
即AD的延长线平分∠CDE. ………--------------5分
(Ⅱ)设O为外接圆圆心,连接AO交BC于H,则AH⊥BC.
连接OC,A由题意∠OAC=∠OCA=150, ∠ACB=750,
∴∠OCH=600.设圆半径为r,则r+r=2+,
得r=2,外接圆的面积为4。----------10分
23. 解:(1), 故的值域为.------ ------4分
(2), , ,
①当时, , -----6分
②当时,, , . -8分
③当时,,, .
综上,-------------------------------------- ---------------------10分
开始
n=n+1
x=2x+1
n≤4
输出x
结束缚
是
否
n=1,x=a
俯视图
正(主)视图
8
5
5
8
侧(左)视图
8
5
5
A
B
C
D
P
频率/组距
15
25
20
10
0
30
次数
a
数 学(文)试题
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的,请用2B铅笔把答题卡上对应题目的答案标号涂黑.
1.已知集合,若,则等于
( )
A. B. C.或 D.或
2、已知 ( )
A. 6 B. 8 C. 10 D.
3.在下列四个命题中,其中为真命题的是 ( )
A. 命题“若,则”的逆否命题是“若,则”
B. 若命题:所有幂函数的图像不过第四象限,命题:所有抛物线的离心率为1,则命题且为真
C. 若命题p:,则
D. 若,则
4.若=-,则cosα+sinα的值为
A.- B.- C. D.
5.设,,则双曲线的离心率的概率是( )
A. B. C. D.
6.函数具有性质( )
A.最大值为,图象关于直线对称
B.最大值为1,图象关于直线对称
C.最大值为,图象关于点对称
D.最大值为1,图象关于点对称
7. 某程序框图如图所示,该程序运行后,输出的值为31,则等于( )
A. B.
C. D.
(第7题图)
8. 椭圆与直线交于、两点,过原点与线段中点的直线的斜率为,则的值为( )
A. B. C. HYPERLINK "http://www./" EMBED Equation.DSMT4 D.
9.若函数的导函数,则使得函数单调递减的一个充分不必要条件是∈( )
10.已知满足,则的最小值是( )
A.0 B. C. D.2
11.已知中,,点为边所在直线上的一个动点,则满足( )
A.最大值为16 B.最小值为4 C.为定值 D.与的位置有关
12.设函数是定义在上的奇函数,且当时,单调递减,若数列是等差数列,且,则的值
( )
A.恒为正数 B.恒为负数 C.恒为0 D.可正可负
第II卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13.若等差数列{}的首项为a1,公差为d,前n项的和为,则数列{}为等差数列,且通项为=a1+(n-1).类似地,请完成下列命题:若各项均为正数的等比数列{}的首项为b1,公比为q,前n项的积为,则数列________为等比数列且通项为_____________.
14. 一个几何体的三视图及其尺寸(单位:cm) ,如图所示,则该几何体的侧面积为 cm.
15. 已知椭圆的左、右焦点分别为,若椭圆上存在点(异于长轴的端点),使得,则该椭圆离心率的取值范围是 .
16.如图,在直角梯形中,, ,动点在内运动(含边界),设,则的取值范围是 .
三、解答题:(本题共6小题,共70分,解答过程应写出文字说明,证明过程或演算步骤).
17.(本小题满分12分)已知中,、、是三个内角、、的对边,关于的不等式的解集是空集.
(1)求角的最大值;
(2)若,的面积,求当角取最大值时的值.
18 ( ).(本小题满分12分)对某校高三年级学生参加社区服务次数进行统计, 随机抽取名学生作为样本,得到这名学生参加社区服务的次数. 根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 频数 频率
24
4 0.1
2 0.05
合计 1
(Ⅰ)求出表中及图中的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间 内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间内的概率.
19.(本小题满分12分)如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
(Ⅰ)求证:DC∥平面PAB;
(Ⅱ)求证:PO⊥平面ABCD;
(Ⅲ)求证:PA⊥BD.
20.(本小题满分12分)
已知椭圆的中心在原点,焦点在轴上,离心率为 ( http: / / www. ),且经过点,直线 ( http: / / www. )交椭圆于不同的两点A,B.
(Ⅰ)求椭圆的方程;
(Ⅱ)求的取值范围;
(Ⅲ)若直线 ( http: / / www. )不过点M,试问是否为定值?并说明理由。
21.(本小题满分12分)已知函数f(x)= HYPERLINK "http://www./" EMBED Equation.DSMT4 在点(-l ,f(-1))的切线方程为x+y+3=0.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)=lnx,求证:g(x)≥f(x)在x∈[1,+∞)上恒成立;
(Ⅲ)已知0<a<b,求证:>.
请考生在第(22)、(23)两题中任选一题做答,如果多做,则按所做的第一题记分。
22.(本小题满分10分)选修4-1:几何证明选讲
已知ABC中,AB=AC, D是 ABC外接圆劣弧AC弧上的点(不与点A,C重合),延长BD至E。
(1)求证:AD的延长线平分CDE;
(2)若BAC=30°,ABC中BC边上的高为2+,求ABC外接圆的面积。
23.(本小题满分10分)选修4-5:不等式选讲
设函数 ( http: / / www. / )
(1)求函数的值域;
(2)若,求成立时的取值范围。
2012年春期高三第二次周考
文科数学参考答案
1—5 DCBCA 6-10 CCACB 11-12 C A
13. || ;=b1() n-1 14. 80
15. 16.
17.解:(1)显然 不合题意,则有,---------------------2分
即, 即, 故,--4分
∴角的最大值为。……………………------------------------------------6分
(2)当=时,,∴-------8分
由余弦定理得,
∴,∴。……………12分
18.解(Ⅰ)由分组内的频数是4,频率是0.1知,,所以
因为频数之和为,所以,. -----4分
因为是对应分组的频率与组距的商,所以------6分
(Ⅱ)因为该校高三学生有240人,分组内的频率是,
所以估计该校高三学生参加社区服务的次数在此区间内的人数为人. ……8分
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有人,
设在区间内的人为,在区间内的人为.
则任选人共有
,15种情况, ……10分
而两人都在内只能是一种,所以所求概率为-12分
20.(Ⅰ),----------------------------------------------------2分
依题意设椭圆方程为: HYPERLINK "http://www." 把点代入,得 HYPERLINK "http://www."
椭圆方程为 HYPERLINK "http://www." ----------------------------------------------------------4分
(Ⅱ)把代入椭圆方程得: HYPERLINK "http://www." ,
由△可得 HYPERLINK "http://www." -----------------------------------------------------6分
(Ⅲ)设,A,B与M不重合,
HYPERLINK "http://www." ,--------------------------------------------------8分
HYPERLINK "http://www." EMBED Equation.DSMT4 ,
HYPERLINK "http://www." EMBED Equation.DSMT4 为定值0.---- --------------12分
21.解:
22.解:(Ⅰ)如图,设F为AD延长线上一点,∵A,B,C,D四点共圆,
∴∠CDF=∠ABC, 又AB=AC ∴∠ABC=∠ACB,且∠ADB=∠ACB, ∴∠ADB=∠CDF,对顶角∠EDF=∠ADB, 故∠EDF=∠CDF,
即AD的延长线平分∠CDE. ………--------------5分
(Ⅱ)设O为外接圆圆心,连接AO交BC于H,则AH⊥BC.
连接OC,A由题意∠OAC=∠OCA=150, ∠ACB=750,
∴∠OCH=600.设圆半径为r,则r+r=2+,
得r=2,外接圆的面积为4。----------10分
23. 解:(1), 故的值域为.------ ------4分
(2), , ,
①当时, , -----6分
②当时,, , . -8分
③当时,,, .
综上,-------------------------------------- ---------------------10分
开始
n=n+1
x=2x+1
n≤4
输出x
结束缚
是
否
n=1,x=a
俯视图
正(主)视图
8
5
5
8
侧(左)视图
8
5
5
A
B
C
D
P
频率/组距
15
25
20
10
0
30
次数
a
同课章节目录
