勾股定理复习题
图片预览



文档简介
(共21张PPT)
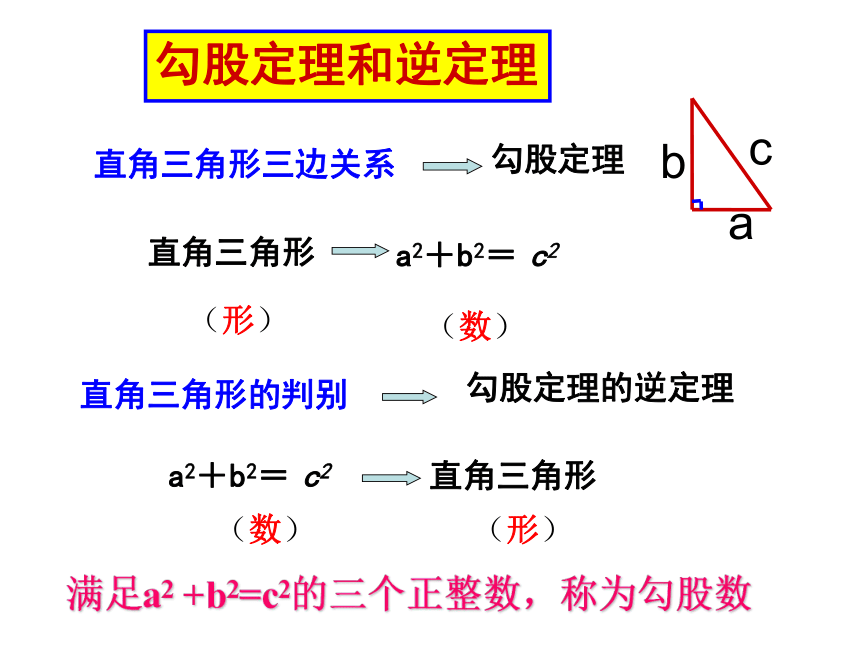
直角三角形三边关系
勾股定理
直角三角形
a2+b2= c2
直角三角形的判别
a2+b2= c2
直角三角形
(形)
(数)
(形)
(数)
勾股定理的逆定理
c
b
a
满足a2 +b2=c2的三个正整数,称为勾股数
勾股定理和逆定理
勾股定理应用一
3.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 周长 = ____.
(2)同上题, =______
4.一个直角三角形的面积54,且其中一条直角边
的长为9,则这个直角三角形的斜边长为_____
5.如上图,直角三角形的面积为24,AC=6,则它的周长为________
A
B
C
24
12
15
24
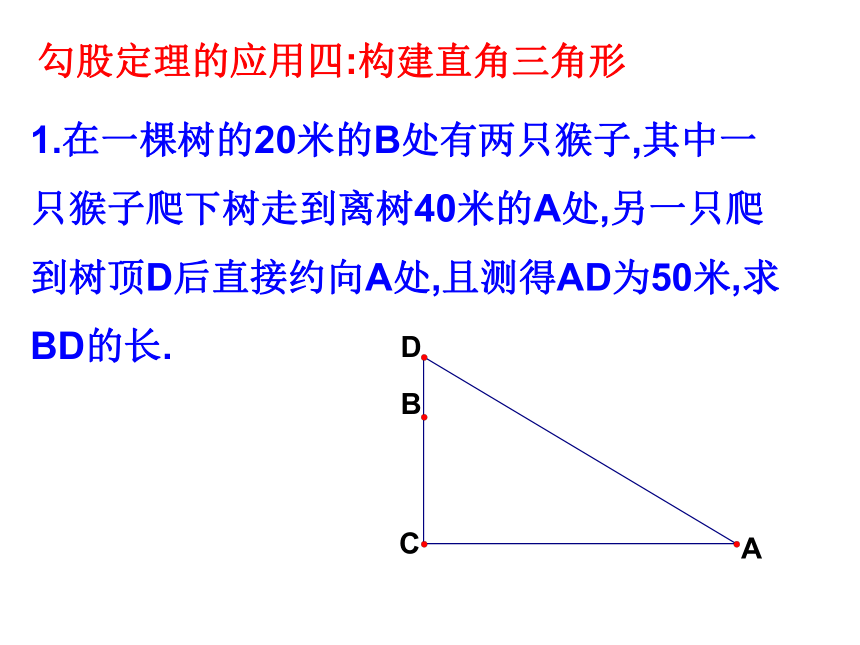
勾股定理的应用四:构建直角三角形
1.在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接约向A处,且测得AD为50米,求BD的长.
5.下列不是一组勾股数的是( )
A、5、12、13 B、
C、12、16、20 D、 7、24、25
6.下面有几组数可以作为直角三角形的边长? ( ) (1) 9, 12, 15 (2) 12,35,36 (3) 15,36 39
(4) 12, 18,32 (5) 5,12,13 (6) 7,24 ,25 A. 2 B. 3 C. 4 D. 5
B
C
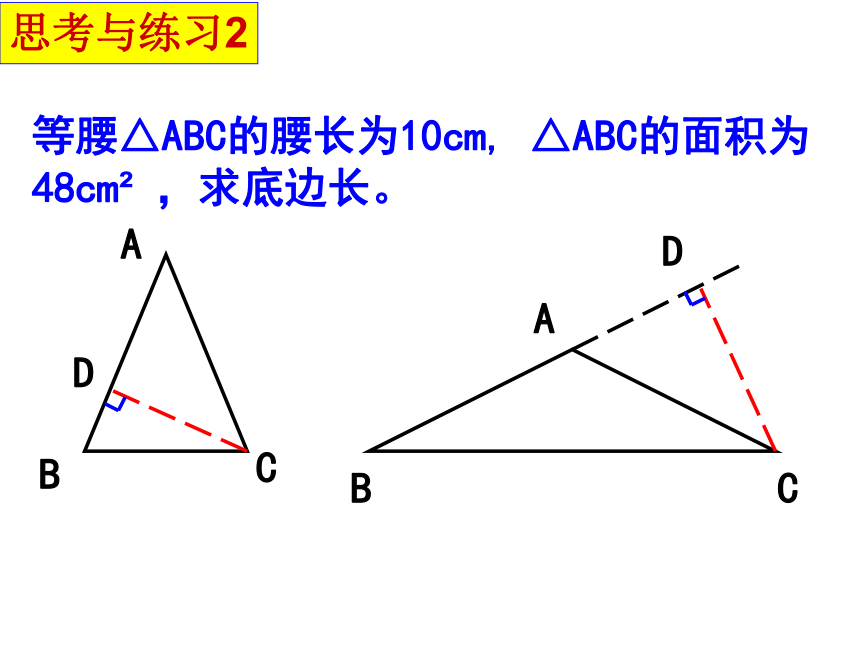
等腰△ABC的腰长为10cm, △ABC的面积为48cm ,求底边长。
A
C
B
D
C
D
A
B
思考与练习2
2、如果△ABC中,∠A:∠B:∠C=1:2:3, 那么BC:AC:AB的值是( )
1:2:3 B. 3:2:1
C. 1: :2 D. 1:2:
1.若三角形的三边长分别等于
,
则此三角形的面积为( )
A.
B.
C.
D.
,2
思考与练习3
B
C
C
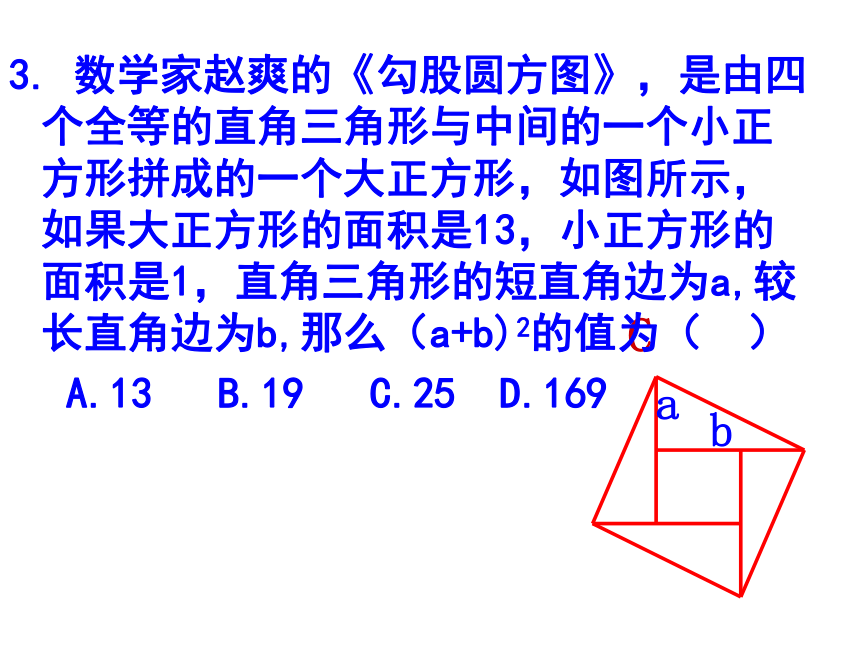
A.13 B.19 C.25 D.169
3. 数学家赵爽的《勾股圆方图》,是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为( )
a
b
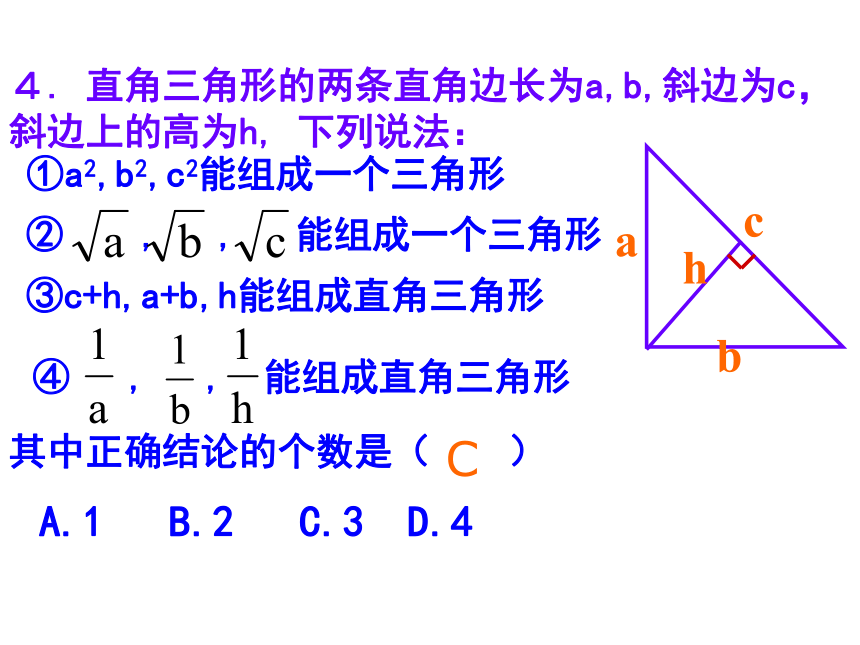
其中正确结论的个数是( )
4. 直角三角形的两条直角边长为a,b,斜边为c,斜边上的高为h, 下列说法:
C
a
b
h
c
①a2,b2,c2能组成一个三角形
② , , 能组成一个三角形
④ , , 能组成直角三角形
③c+h,a+b,h能组成直角三角形
A.1 B.2 C.3 D.4
如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
x
10-x
6
10-x
基础回顾
长方形ABCD如图折叠,使点D落在BC边上的点F处,
已知AB=8,BC=10,求折痕AE的长。
A
B
C
D
F
E
8
10
8
10
10
6
x
x
8-x
4
探究3:
折叠长方形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
练习&3
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
折叠长方形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
练习&3
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2 。若△ABC不是直角三角形,如图(2)和(3),请你类比勾股定理,试猜想 a2+b2 与c2的关系,并证明你的结论。
A
A
A
B
B
B
C
C
C
(1)
(2)
(3)
a
a
a
b
b
b
c
c
c
拓展训练
A
a
b
c
B
C
D
证明: 如图,过点A作AD⊥BC于点D
设CD=x,
b2-x2=AD2=c2-(a-x)2
即
b2-x2=c2-a2+2ax-x2
∴a2+ b2= c2+2ax
∵a>0,x>0,
∴a2+b2> c2.
∴2ax>0
则有BD=a-x.
根据勾股定理,得
x
a-x
猜想:a2+b2> c2
B
C
D
证明: 如图,过点B作B D⊥AC于点D
设CD=x,
即
a2+b2+2bx= c2
∴a2+ b2= c2-2bx
∵b>0,x>0,
∴a2+b2< c2.
∴2bx>0
则有BD2=a2-x2
根据勾股定理,得
x
A
a
b
c
(b+x)2+a2-x2= c2
猜想:a2+b2< c2
B
A
C
b
a
c
B
A
C
b
a
c
B
A
C
b
a
c
锐
锐
钝
钝
归纳小结
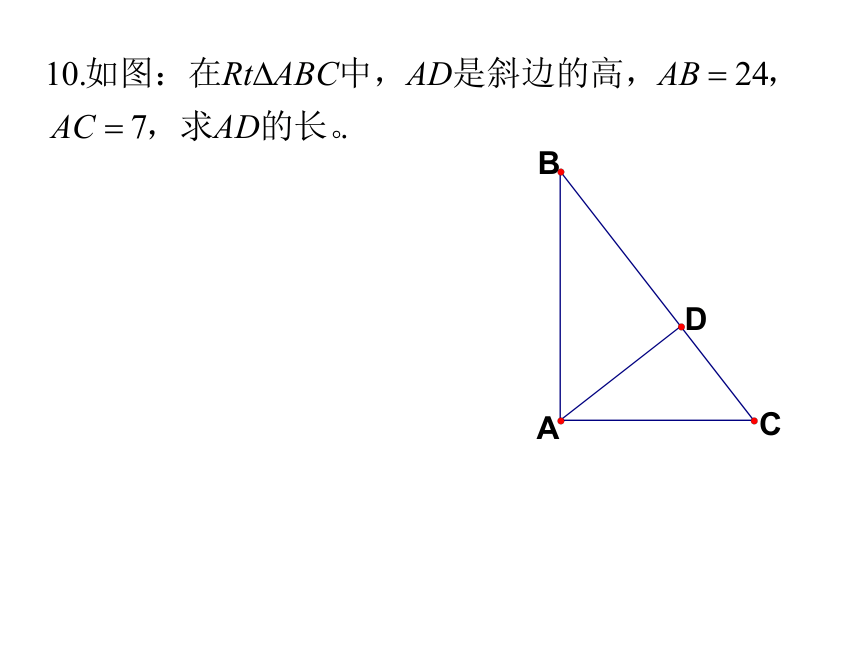
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
∟
D
∟
D
A
B
C
1.已知:直角三角形的三边长分别是3,4,X,则X2=
25
或7
A
B
C
10
17
8
17
10
8
分类思想
2.如图,铁路上A、B两点相距25km, C、D为两村庄,DA垂直AB于A,CB垂直AB于B,已知AD=15km,BC=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站建
在距A站多少千米处?
例2:如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
50
40
30
40
50
30
x
x
一根70cm的木棒,要放在长、宽、高分别是50cm,40cm,30cm的长方体木箱中,能放进去吗
直角三角形三边关系
勾股定理
直角三角形
a2+b2= c2
直角三角形的判别
a2+b2= c2
直角三角形
(形)
(数)
(形)
(数)
勾股定理的逆定理
c
b
a
满足a2 +b2=c2的三个正整数,称为勾股数
勾股定理和逆定理
勾股定理应用一
3.已知直角三角形ABC中,
(1)若AC=8,AB=10,则 周长 = ____.
(2)同上题, =______
4.一个直角三角形的面积54,且其中一条直角边
的长为9,则这个直角三角形的斜边长为_____
5.如上图,直角三角形的面积为24,AC=6,则它的周长为________
A
B
C
24
12
15
24
勾股定理的应用四:构建直角三角形
1.在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接约向A处,且测得AD为50米,求BD的长.
5.下列不是一组勾股数的是( )
A、5、12、13 B、
C、12、16、20 D、 7、24、25
6.下面有几组数可以作为直角三角形的边长? ( ) (1) 9, 12, 15 (2) 12,35,36 (3) 15,36 39
(4) 12, 18,32 (5) 5,12,13 (6) 7,24 ,25 A. 2 B. 3 C. 4 D. 5
B
C
等腰△ABC的腰长为10cm, △ABC的面积为48cm ,求底边长。
A
C
B
D
C
D
A
B
思考与练习2
2、如果△ABC中,∠A:∠B:∠C=1:2:3, 那么BC:AC:AB的值是( )
1:2:3 B. 3:2:1
C. 1: :2 D. 1:2:
1.若三角形的三边长分别等于
,
则此三角形的面积为( )
A.
B.
C.
D.
,2
思考与练习3
B
C
C
A.13 B.19 C.25 D.169
3. 数学家赵爽的《勾股圆方图》,是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为( )
a
b
其中正确结论的个数是( )
4. 直角三角形的两条直角边长为a,b,斜边为c,斜边上的高为h, 下列说法:
C
a
b
h
c
①a2,b2,c2能组成一个三角形
② , , 能组成一个三角形
④ , , 能组成直角三角形
③c+h,a+b,h能组成直角三角形
A.1 B.2 C.3 D.4
如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
x
10-x
6
10-x
基础回顾
长方形ABCD如图折叠,使点D落在BC边上的点F处,
已知AB=8,BC=10,求折痕AE的长。
A
B
C
D
F
E
8
10
8
10
10
6
x
x
8-x
4
探究3:
折叠长方形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
练习&3
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
折叠长方形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=4,BC=3,求AG的长。
D
A
G
B
C
E
练习&3
4
x
3
4
3
4-x
x
3
你还能用其他方法求AG的长吗?
△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2 。若△ABC不是直角三角形,如图(2)和(3),请你类比勾股定理,试猜想 a2+b2 与c2的关系,并证明你的结论。
A
A
A
B
B
B
C
C
C
(1)
(2)
(3)
a
a
a
b
b
b
c
c
c
拓展训练
A
a
b
c
B
C
D
证明: 如图,过点A作AD⊥BC于点D
设CD=x,
b2-x2=AD2=c2-(a-x)2
即
b2-x2=c2-a2+2ax-x2
∴a2+ b2= c2+2ax
∵a>0,x>0,
∴a2+b2> c2.
∴2ax>0
则有BD=a-x.
根据勾股定理,得
x
a-x
猜想:a2+b2> c2
B
C
D
证明: 如图,过点B作B D⊥AC于点D
设CD=x,
即
a2+b2+2bx= c2
∴a2+ b2= c2-2bx
∵b>0,x>0,
∴a2+b2< c2.
∴2bx>0
则有BD2=a2-x2
根据勾股定理,得
x
A
a
b
c
(b+x)2+a2-x2= c2
猜想:a2+b2< c2
B
A
C
b
a
c
B
A
C
b
a
c
B
A
C
b
a
c
锐
锐
钝
钝
归纳小结
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC
∟
D
∟
D
A
B
C
1.已知:直角三角形的三边长分别是3,4,X,则X2=
25
或7
A
B
C
10
17
8
17
10
8
分类思想
2.如图,铁路上A、B两点相距25km, C、D为两村庄,DA垂直AB于A,CB垂直AB于B,已知AD=15km,BC=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站建
在距A站多少千米处?
例2:如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
50
40
30
40
50
30
x
x
一根70cm的木棒,要放在长、宽、高分别是50cm,40cm,30cm的长方体木箱中,能放进去吗
