勾股定理的逆定理
图片预览








文档简介
(共26张PPT)
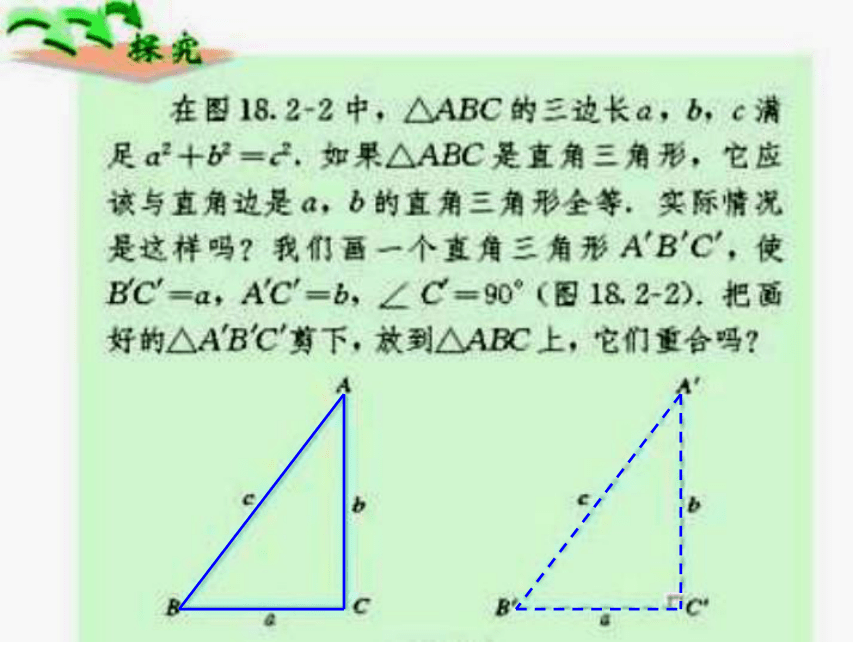
古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。
三角形的三边有什么关系呢?
(1)
(3)
(2)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
你能猜想出其中的数学道理吗?
32 + 42 = 52
直角三角形
下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13; 7,24,25; 8,15,17。
(1)这三组数都满足
吗?
(2)它们都是直角三角形吗?
动手画一画
由以上实践,我们发现:
如果围成的三角形的三边分别是3,4,5,有下列的关系:“ ”,那么围成的三角形是直角三角形.
做一做
如果三角形的三边分别是5cm,12cm,13cm,有下列的关系: .
那么画出的三角形是直角三角形吗
换成三边分别是6cm,8cm,10cm
呢
勾股定理的逆定理
如果三角形的三边长a,b,c有关系
那么这个三角形是直角三角形.
能够成为直角三角形三边长的三个正整数,称为勾股数(或勾股弦数)。
猜想
命题2 如果三角形的三边长a,b,c满足
a2+b2=c2,
那么这个三角形是直角三角形.
命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2,
互逆命题 在一对命题中,第一个命题的题设恰为第二个命题的结论,而第一个命题的结论恰为第二个命题的题设,像这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。且边C年所对的角为直角。
a2 + b2 = c2
互逆命题
逆定理
定理
勾股定理的逆定理 如果三角形的三边长a,b,c满足
a2+b2=c2,
那么这个三角形是直角三角形.
说明:(1)一般地,如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理为互逆定理;
(2)勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
(3)勾股定理的逆定理主要的应用是把数转化为形,通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形,它可作为直角三角形的判定依据.
例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17
例题解析
(2) a=13 , b =15 , c=14
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。
解:∵152+82=225+64=289
172=289
∴ 152+82=172
∴这个三角形是直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.
3、以小组为单位,每位同学自己找一组
勾股数,那一组找的最快最多就算获胜。
练习
1.如果三条线段长a,b,c满足a2=c2-b2,这三条线段组成的三角形是不是直角三角形?为什么?
2.以下各组数为边长,能组成直角三角形的是( ).
A.5,6,7 B.10,8,4
C.7,25,24 D.9,17,15
3.以下各组正数为边长,能组成直角三角形的是( ).
A.a-1,2a,a+1 B.a-1,2 ,a+1
C.a-1, ,a+1 D.a-1, a,a+1
C
B
4.说出下列命题的逆命题,这些命题的逆命题成立吗?
(1)两直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)等腰三角形的底角相等.
练习
5.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2-1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
练习
3.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状.
(二)解答题:
练 习
这个三角形是直角三角形.
(二)解答题:
1.已知:a=m2-n2,b=2mn,c=m2+n2
(m、n为正整数,m>n).
试判定由a、b、c组成的三角形是不是直
角三角形.
不是
练 习
例 3.在△ABC中,a=15, b=17, c=8,求此三角形的面积。
∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为
7.如图:AD⊥CD , AC⊥BC ,AB=13, CD=3 , AD=4 。求:(1)求AC长
(2)求BC长
8.如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)∠ACB的度数。
B
A
D
C
13
3
4
B
A
D
C
12
13
3
4
勾股定理与逆定理的综合运用
9.如图, AC⊥BC ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)求 的面积。
B
A
D
C
12
13
3
4
3、△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
A
B
C
a
b
c
S1
S2
S3
思维训练
三、正方体中的最值问题
例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1
A
B
分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).
C
A
B
C
2
1
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
互逆命题
(逆定理)
(互逆定理)
收获 心得
谈谈这节课你的收获吧!
古埃及人把一根绳子打上等距离的13个结,然后把第1个结和第13个结用木桩钉在一起,再分别用木桩把第4个结和第8个结钉牢(拉直绳子)。
三角形的三边有什么关系呢?
(1)
(3)
(2)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
你能猜想出其中的数学道理吗?
32 + 42 = 52
直角三角形
下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13; 7,24,25; 8,15,17。
(1)这三组数都满足
吗?
(2)它们都是直角三角形吗?
动手画一画
由以上实践,我们发现:
如果围成的三角形的三边分别是3,4,5,有下列的关系:“ ”,那么围成的三角形是直角三角形.
做一做
如果三角形的三边分别是5cm,12cm,13cm,有下列的关系: .
那么画出的三角形是直角三角形吗
换成三边分别是6cm,8cm,10cm
呢
勾股定理的逆定理
如果三角形的三边长a,b,c有关系
那么这个三角形是直角三角形.
能够成为直角三角形三边长的三个正整数,称为勾股数(或勾股弦数)。
猜想
命题2 如果三角形的三边长a,b,c满足
a2+b2=c2,
那么这个三角形是直角三角形.
命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2,
互逆命题 在一对命题中,第一个命题的题设恰为第二个命题的结论,而第一个命题的结论恰为第二个命题的题设,像这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。且边C年所对的角为直角。
a2 + b2 = c2
互逆命题
逆定理
定理
勾股定理的逆定理 如果三角形的三边长a,b,c满足
a2+b2=c2,
那么这个三角形是直角三角形.
说明:(1)一般地,如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理为互逆定理;
(2)勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
(3)勾股定理的逆定理主要的应用是把数转化为形,通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形,它可作为直角三角形的判定依据.
例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17
例题解析
(2) a=13 , b =15 , c=14
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。
解:∵152+82=225+64=289
172=289
∴ 152+82=172
∴这个三角形是直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a:b: c=3:4:5 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.
3、以小组为单位,每位同学自己找一组
勾股数,那一组找的最快最多就算获胜。
练习
1.如果三条线段长a,b,c满足a2=c2-b2,这三条线段组成的三角形是不是直角三角形?为什么?
2.以下各组数为边长,能组成直角三角形的是( ).
A.5,6,7 B.10,8,4
C.7,25,24 D.9,17,15
3.以下各组正数为边长,能组成直角三角形的是( ).
A.a-1,2a,a+1 B.a-1,2 ,a+1
C.a-1, ,a+1 D.a-1, a,a+1
C
B
4.说出下列命题的逆命题,这些命题的逆命题成立吗?
(1)两直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)等腰三角形的底角相等.
练习
5.古希腊的哲学家柏拉图曾指出,如果m表示大于1的整数,a=2m,b=m2-1,c=m2+1,那么a,b,c为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
练习
3.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状.
(二)解答题:
练 习
这个三角形是直角三角形.
(二)解答题:
1.已知:a=m2-n2,b=2mn,c=m2+n2
(m、n为正整数,m>n).
试判定由a、b、c组成的三角形是不是直
角三角形.
不是
练 习
例 3.在△ABC中,a=15, b=17, c=8,求此三角形的面积。
∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为
7.如图:AD⊥CD , AC⊥BC ,AB=13, CD=3 , AD=4 。求:(1)求AC长
(2)求BC长
8.如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)∠ACB的度数。
B
A
D
C
13
3
4
B
A
D
C
12
13
3
4
勾股定理与逆定理的综合运用
9.如图, AC⊥BC ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)求 的面积。
B
A
D
C
12
13
3
4
3、△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
A
B
C
a
b
c
S1
S2
S3
思维训练
三、正方体中的最值问题
例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1
A
B
分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).
C
A
B
C
2
1
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
互逆命题
(逆定理)
(互逆定理)
收获 心得
谈谈这节课你的收获吧!
