2020-2021学年北师大版七年级下册第五章生活中的轴对称 测试卷(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级下册第五章生活中的轴对称 测试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 451.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 11:20:44 | ||
图片预览


文档简介
七年级第五章水平测试卷
一、选择题(本大题10小题,每小题3分,共30分)
1.下列图案是轴对称图形的是( )
2.
下列图形中,不一定是轴对称图形的是( )
A.
互相垂直的两条直线构成的图形
B.
一条直线和直线外一点构成的图形
C.
有一个内角为30°,另一个内角为120°的三角形
D.
有一个内角为60°的三角形
3.下列图形中,对称轴最多的图形是( )
A.正方形
B.等边三角形
C.等腰梯形
D.等腰三角形
4.
如图5-1,将△ABC沿直线DE折叠后,使得点B与点A重合.
已知AC=5
cm,△ADC的周长为17
cm,则BC的长为( )
A.
7
cm
B.
10
cm
C.
12
cm
D.
22
cm
5.
以下说法中,正确的是( )
①等腰三角形的一边长为4cm,一边长为9cm,则它的周长为17cm或22cm;②三角形的一个外角等于两个内角的和;③有两边和一角对应相等的两个三角形全等;④等边三角形是轴对称图形;⑤如果三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A.
①②③
B.
①③⑤
C.
②④⑤
D.
④⑤
6.如图5-2所示是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.
若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是( )
A.
1号袋
B.
2号袋
C.
3号袋
D.
4号袋
7.
下列说法正确的是( )
A.
等腰三角形的高、中线、角平分线互相重合
B.
顶角相等的两个等腰三角形全等
C.
等腰三角形的一边长不可以是另一边长的2倍
D.
等腰三角形的两个底角相等
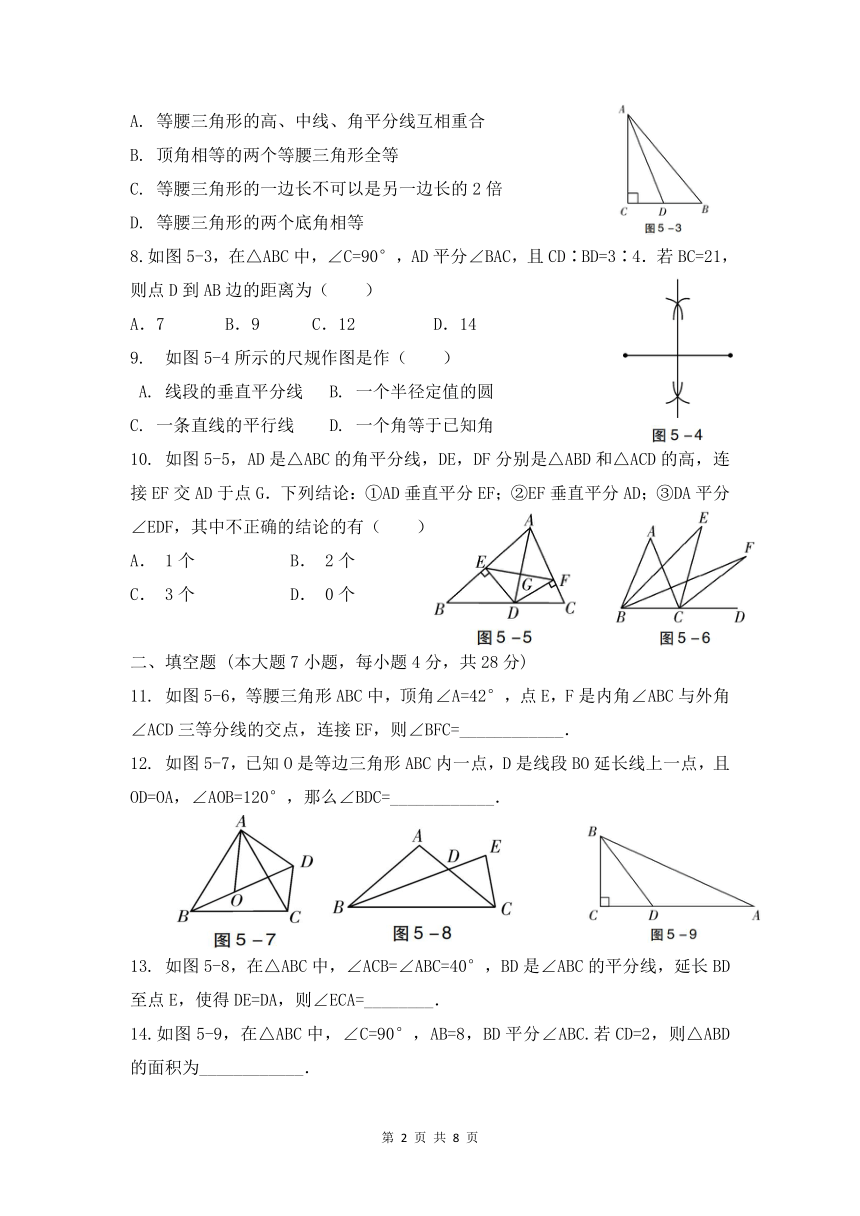
8.如图5-3,在△ABC中,∠C=90°,AD平分∠BAC,且CD∶BD=3∶4.若BC=21,则点D到AB边的距离为( )
A.7
B.9
C.12
D.14
9.
如图5-4所示的尺规作图是作( )
A.
线段的垂直平分线
B.
一个半径定值的圆
C.
一条直线的平行线
D.
一个角等于已知角
10.
如图5-5,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于点G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③DA平分∠EDF,其中不正确的结论的有( )
A.
1个
B.
2个
C.
3个
D.
0个
二、填空题
(本大题7小题,每小题4分,共28分)
11.
如图5-6,等腰三角形ABC中,顶角∠A=42°,点E,F是内角∠ABC与外角∠ACD三等分线的交点,连接EF,则∠BFC=____________.
12.
如图5-7,已知O是等边三角形ABC内一点,D是线段BO延长线上一点,且OD=OA,∠AOB=120°,那么∠BDC=____________.
13.
如图5-8,在△ABC中,∠ACB=∠ABC=40°,BD是∠ABC的平分线,延长BD至点E,使得DE=DA,则∠ECA=________.
14.如图5-9,在△ABC中,∠C=90°,AB=8,BD平分∠ABC.若CD=2,则△ABD的面积为____________.
15.
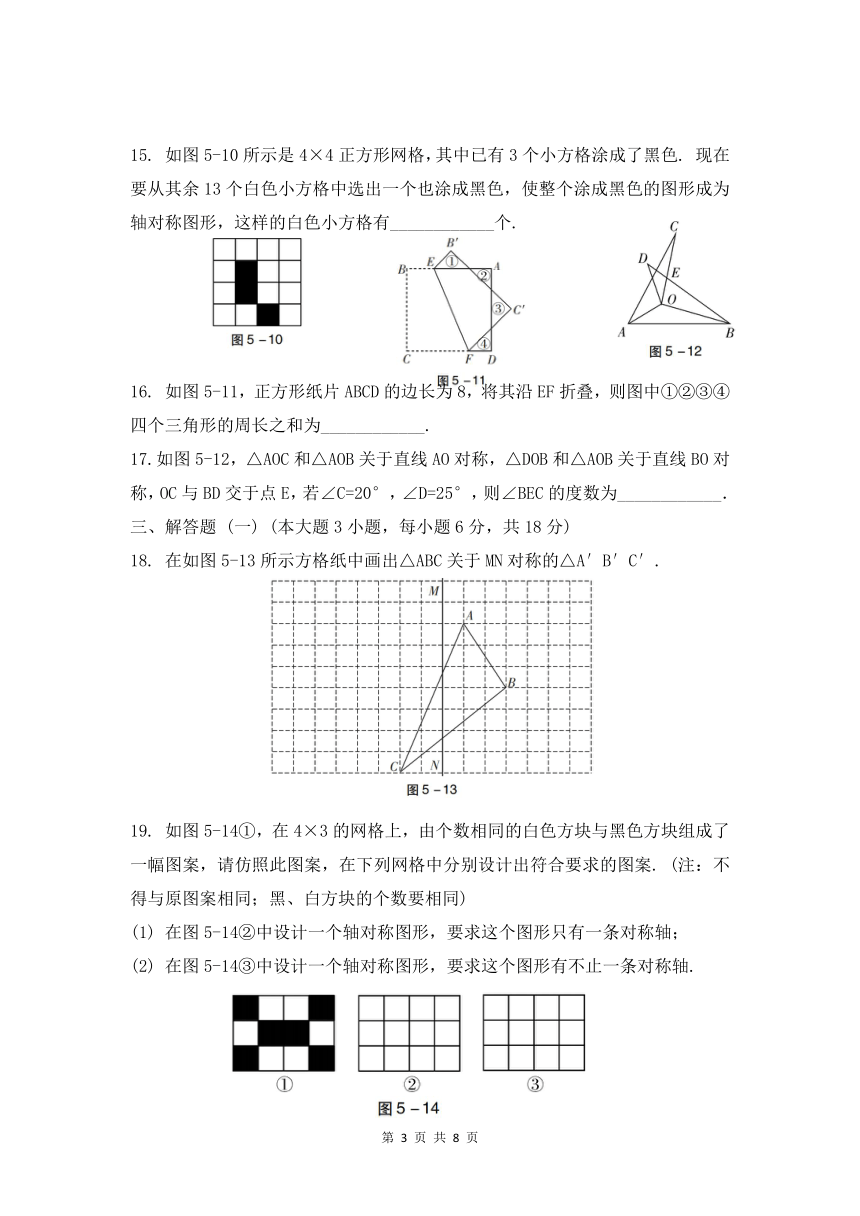
如图5-10所示是4×4正方形网格,其中已有3个小方格涂成了黑色.
现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有____________个.
16.
如图5-11,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为____________.
17.如图5-12,△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,OC与BD交于点E,若∠C=20°,∠D=25°,则∠BEC的度数为____________.
三、解答题
(一)
(本大题3小题,每小题6分,共18分)
18.
在如图5-13所示方格纸中画出△ABC关于MN对称的△A′B′C′.
19.
如图5-14①,在4×3的网格上,由个数相同的白色方块与黑色方块组成了一幅图案,请仿照此图案,在下列网格中分别设计出符合要求的图案.
(注:不得与原图案相同;黑、白方块的个数要相同)
(1)
在图5-14②中设计一个轴对称图形,要求这个图形只有一条对称轴;
(2)
在图5-14③中设计一个轴对称图形,要求这个图形有不止一条对称轴.
20.
在如图5-15,等腰三角形ABC中,AB=AC,BC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于点D,AD=4,点E是AB的中点,连接DE.
(1)求∠B的度数;
(2)求三角形BDE的面积.
四、解答题
(二)
(本大题3小题,每小题8分,共24分)
21.
如图5-16,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N,试说明:PM=PN.
22.
如图5-17,在△ABC中,AB=AC,D,E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)试说明:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
23.
如图5-18,已知△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F,连接AF.
试说明:∠BAF=∠ACF.
五、解答题
(三)
(本大题2小题,每小题10分,共20分)
24.
如图5-19,在长方形ABCD的台球桌上有三个台球M,N,P,且M,N,P在同一直线上.现在要求主球P在不撞击其他彩球的情况下击彩球M(不能跳过N击M),问能否击中M?若不能,请说明理由;若能击中M,请画出主球P的运动路线,画出两种不同的击法,
并简要地说明理由.
25.
如图5-20,△ABC中,AB=BC=AC=12
cm,现有两点M,N分别从点A,点B同时出发,沿三角形的边运动,已知点M的速度为1
cm/s,点N的速度为2
cm/s.当点N第一次到达B点时,点M,N同时停止运动.
(1)点M,N运动几秒后,M,N两点重合?
(2)点M,N运动几秒后,可得到等边三角形AMN?
(3)当点M,N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如果能,请求出此时M,N运动的时间.
参考答案
1-10BDACD
BDBAA
11.14°
12.60°
13.40°
14.8
15.3
16.32
17.110°
略.
解:(1)
如答图5-1.(2)
如答图5-2.(答案不唯一)
20.解:(1)因为AB=AC,∠BAC=100°,
所以∠B=∠C=
(180°-∠A)=40°.
(2)因为AB=AC,AD是∠BAC的平分线,
所以AD⊥BC.
因为点E是AB的中点,
所以S△AED=S△BED=
S△ABD=
×
AD·BD=
×
×4×4=4.
21.解:因为BD为∠ABC的平分线,
所以∠ABD=∠CBD.
在△ABD和△CBD中,
AB=BC,∠ABD=∠CBD,BD=BD,
所以△ABD≌△CBD(SAS).
所以∠ADB=∠CDB.
因为点P在BD上,PM⊥AD,PN⊥CD,所以PM=PN.
22.解:(1)因为以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,所以AD=AD′.
因为在△ABD和△ACD′中,
所以△ABD≌△ACD′(SSS).
(2)因为△ABD≌△ACD′,所以∠BAD=∠CAD′.
所以∠BAC=∠DAD′=120°.
因为以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
所以∠DAE=∠D′AE=
∠DAD′=60°,即∠DAE=60°
23.解:因为AD是∠BAC的平分线,
所以∠1=∠2.
因为FE是AD的垂直平分线,
所以FA=FD.
所以∠FAD=∠FDA.
因为∠BAF=∠FAD+∠1,∠ACF=∠FDA+∠2,
所以∠BAF=∠ACF.
24.解:(1)作点P关于BC的对称点P′,理由略,如答图5-3①.
(2)作M关于AD的对称点M′,理由略,如答图5-3②.
25.解:(1)设点M,N运动x
s后,M,N两点重合.
x×1+12=2x.解得x=12.
(2)设点M,N运动t
s后,可得到等边三角形AMN,
如答图5-4①,
AM=t×1=t,AN=AB-BN=12-2t.
因为△AMN是等边三角形,所以t=12-2t.
解得t=4.所以点M,N运动4
s后,可得到等边三角形AMN.
(3)当点M,N在BC边上运动时,可以得到以MN为底边的等腰三角形.
由(1)知,12
s时M,N两点重合,恰好在C处,
如答图5-4②,假设△AMN是等腰三角形,所以AN=AM.
所以∠AMN=∠ANM.所以∠AMC=∠ANB.
因为AB=BC=AC,所以△ACB是等边三角形.所以∠C=∠B.
在△ACM和△ABN中,
所以△ACM≌△ABN(AAS).所以CM=BN.
设当点M,N在BC边上运动的时间为y
s时,△AMN是等腰三角形,
所以CM=y-12,NB=36-2y,由CM=NB,得y-12=36-2y.解得y=16.故假设成立.
所以当点M,N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M,N运动的时间为16
s.
一、选择题(本大题10小题,每小题3分,共30分)
1.下列图案是轴对称图形的是( )
2.
下列图形中,不一定是轴对称图形的是( )
A.
互相垂直的两条直线构成的图形
B.
一条直线和直线外一点构成的图形
C.
有一个内角为30°,另一个内角为120°的三角形
D.
有一个内角为60°的三角形
3.下列图形中,对称轴最多的图形是( )
A.正方形
B.等边三角形
C.等腰梯形
D.等腰三角形
4.
如图5-1,将△ABC沿直线DE折叠后,使得点B与点A重合.
已知AC=5
cm,△ADC的周长为17
cm,则BC的长为( )
A.
7
cm
B.
10
cm
C.
12
cm
D.
22
cm
5.
以下说法中,正确的是( )
①等腰三角形的一边长为4cm,一边长为9cm,则它的周长为17cm或22cm;②三角形的一个外角等于两个内角的和;③有两边和一角对应相等的两个三角形全等;④等边三角形是轴对称图形;⑤如果三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A.
①②③
B.
①③⑤
C.
②④⑤
D.
④⑤
6.如图5-2所示是一个台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.
若一个球按图中所示的方向被击出(球可以经过多次反射),则该球最后将落入的球袋是( )
A.
1号袋
B.
2号袋
C.
3号袋
D.
4号袋
7.
下列说法正确的是( )
A.
等腰三角形的高、中线、角平分线互相重合
B.
顶角相等的两个等腰三角形全等
C.
等腰三角形的一边长不可以是另一边长的2倍
D.
等腰三角形的两个底角相等
8.如图5-3,在△ABC中,∠C=90°,AD平分∠BAC,且CD∶BD=3∶4.若BC=21,则点D到AB边的距离为( )
A.7
B.9
C.12
D.14
9.
如图5-4所示的尺规作图是作( )
A.
线段的垂直平分线
B.
一个半径定值的圆
C.
一条直线的平行线
D.
一个角等于已知角
10.
如图5-5,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于点G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③DA平分∠EDF,其中不正确的结论的有( )
A.
1个
B.
2个
C.
3个
D.
0个
二、填空题
(本大题7小题,每小题4分,共28分)
11.
如图5-6,等腰三角形ABC中,顶角∠A=42°,点E,F是内角∠ABC与外角∠ACD三等分线的交点,连接EF,则∠BFC=____________.
12.
如图5-7,已知O是等边三角形ABC内一点,D是线段BO延长线上一点,且OD=OA,∠AOB=120°,那么∠BDC=____________.
13.
如图5-8,在△ABC中,∠ACB=∠ABC=40°,BD是∠ABC的平分线,延长BD至点E,使得DE=DA,则∠ECA=________.
14.如图5-9,在△ABC中,∠C=90°,AB=8,BD平分∠ABC.若CD=2,则△ABD的面积为____________.
15.
如图5-10所示是4×4正方形网格,其中已有3个小方格涂成了黑色.
现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有____________个.
16.
如图5-11,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为____________.
17.如图5-12,△AOC和△AOB关于直线AO对称,△DOB和△AOB关于直线BO对称,OC与BD交于点E,若∠C=20°,∠D=25°,则∠BEC的度数为____________.
三、解答题
(一)
(本大题3小题,每小题6分,共18分)
18.
在如图5-13所示方格纸中画出△ABC关于MN对称的△A′B′C′.
19.
如图5-14①,在4×3的网格上,由个数相同的白色方块与黑色方块组成了一幅图案,请仿照此图案,在下列网格中分别设计出符合要求的图案.
(注:不得与原图案相同;黑、白方块的个数要相同)
(1)
在图5-14②中设计一个轴对称图形,要求这个图形只有一条对称轴;
(2)
在图5-14③中设计一个轴对称图形,要求这个图形有不止一条对称轴.
20.
在如图5-15,等腰三角形ABC中,AB=AC,BC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于点D,AD=4,点E是AB的中点,连接DE.
(1)求∠B的度数;
(2)求三角形BDE的面积.
四、解答题
(二)
(本大题3小题,每小题8分,共24分)
21.
如图5-16,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N,试说明:PM=PN.
22.
如图5-17,在△ABC中,AB=AC,D,E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)试说明:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
23.
如图5-18,已知△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F,连接AF.
试说明:∠BAF=∠ACF.
五、解答题
(三)
(本大题2小题,每小题10分,共20分)
24.
如图5-19,在长方形ABCD的台球桌上有三个台球M,N,P,且M,N,P在同一直线上.现在要求主球P在不撞击其他彩球的情况下击彩球M(不能跳过N击M),问能否击中M?若不能,请说明理由;若能击中M,请画出主球P的运动路线,画出两种不同的击法,
并简要地说明理由.
25.
如图5-20,△ABC中,AB=BC=AC=12
cm,现有两点M,N分别从点A,点B同时出发,沿三角形的边运动,已知点M的速度为1
cm/s,点N的速度为2
cm/s.当点N第一次到达B点时,点M,N同时停止运动.
(1)点M,N运动几秒后,M,N两点重合?
(2)点M,N运动几秒后,可得到等边三角形AMN?
(3)当点M,N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如果能,请求出此时M,N运动的时间.
参考答案
1-10BDACD
BDBAA
11.14°
12.60°
13.40°
14.8
15.3
16.32
17.110°
略.
解:(1)
如答图5-1.(2)
如答图5-2.(答案不唯一)
20.解:(1)因为AB=AC,∠BAC=100°,
所以∠B=∠C=
(180°-∠A)=40°.
(2)因为AB=AC,AD是∠BAC的平分线,
所以AD⊥BC.
因为点E是AB的中点,
所以S△AED=S△BED=
S△ABD=
×
AD·BD=
×
×4×4=4.
21.解:因为BD为∠ABC的平分线,
所以∠ABD=∠CBD.
在△ABD和△CBD中,
AB=BC,∠ABD=∠CBD,BD=BD,
所以△ABD≌△CBD(SAS).
所以∠ADB=∠CDB.
因为点P在BD上,PM⊥AD,PN⊥CD,所以PM=PN.
22.解:(1)因为以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,所以AD=AD′.
因为在△ABD和△ACD′中,
所以△ABD≌△ACD′(SSS).
(2)因为△ABD≌△ACD′,所以∠BAD=∠CAD′.
所以∠BAC=∠DAD′=120°.
因为以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
所以∠DAE=∠D′AE=
∠DAD′=60°,即∠DAE=60°
23.解:因为AD是∠BAC的平分线,
所以∠1=∠2.
因为FE是AD的垂直平分线,
所以FA=FD.
所以∠FAD=∠FDA.
因为∠BAF=∠FAD+∠1,∠ACF=∠FDA+∠2,
所以∠BAF=∠ACF.
24.解:(1)作点P关于BC的对称点P′,理由略,如答图5-3①.
(2)作M关于AD的对称点M′,理由略,如答图5-3②.
25.解:(1)设点M,N运动x
s后,M,N两点重合.
x×1+12=2x.解得x=12.
(2)设点M,N运动t
s后,可得到等边三角形AMN,
如答图5-4①,
AM=t×1=t,AN=AB-BN=12-2t.
因为△AMN是等边三角形,所以t=12-2t.
解得t=4.所以点M,N运动4
s后,可得到等边三角形AMN.
(3)当点M,N在BC边上运动时,可以得到以MN为底边的等腰三角形.
由(1)知,12
s时M,N两点重合,恰好在C处,
如答图5-4②,假设△AMN是等腰三角形,所以AN=AM.
所以∠AMN=∠ANM.所以∠AMC=∠ANB.
因为AB=BC=AC,所以△ACB是等边三角形.所以∠C=∠B.
在△ACM和△ABN中,
所以△ACM≌△ABN(AAS).所以CM=BN.
设当点M,N在BC边上运动的时间为y
s时,△AMN是等腰三角形,
所以CM=y-12,NB=36-2y,由CM=NB,得y-12=36-2y.解得y=16.故假设成立.
所以当点M,N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M,N运动的时间为16
s.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
