第十八章 平行四边形 单元达标+培优检测题(含答案)
文档属性
| 名称 | 第十八章 平行四边形 单元达标+培优检测题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十八章平行四边形单元达标+培优检测题
(时间:100分钟 满分:100+20分)
一、选择题(每小题3分,共30分)
1.若平行四边形中两个内角的度数比为1∶3,则其中较小的内角是( )
A.
30°
B.45°
C.60°
D.75°
2.如图,已知四边形ABCD是平行四边形,对角线AC,BD相交于点O,
E是BC的中点,以下说法错误的是( )
A.OE=DC
B.OA=OC
C.∠BOE=∠OBA
D.∠OBE=∠OCE
3.如图,矩形ABCD的对角线AC=8
cm,∠AOD=120°,则AD的长为( )
A.4
cm
B.6
cm
C.3
cm
D.5
cm
4.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
5.下列说法正确的有( )
①有一个角是直角的平行四边形是矩形
②
四个角都相等的四边形是矩形
③两条对角线相等的四边形是矩形
④有一组对边相等,一组对角是直角的四边形是矩形
A.4个
B.3个
C.2个
D.1个
6.如图,已知点E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )
A.20°
B.25°
C.30°
D.35°
7.在ABCD中,AB=3,BC=4,当ABCD的面积最大时,下结论错误的是( )
A.AC=5
B.∠A+∠C=180°
C.AC⊥BD
D.AC=BD.
8.红丝带是关注艾滋病防治问题的国际性标志,人们将红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,如图所示.红丝带重叠部分形成的图形是( )
A、正方形
B、等腰梯形
C、菱形
D、矩形
第6题图
第8题图
第9题图
第10题图
9.如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE:∠BAE=1:2,则∠CAE的度数为(
)
A.
30°
B.
40°
C.45°
D.
50°
10.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上点M处,延长BC,EF交于点N,有下列四个结论:①DF=CF;
②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF,其中正确的结论是( )
A.①②③
B.①②④
C.②③④
D.①②③④
二、填空题(每小题3分,共18分)
11.如图,在ABCD中,AB=5,AC=6,当BD=_______时,四边形ABCD是菱形.
12.如图,正方形ABCD中,E是对角线BD上一点,且BE=BC,则∠DCE的度数是_______度.
第11题图
第12题图
第14题图
第15题图
13.在四边形ABCD中,AD∥BC,分别添加下列条件之一:①AB∥CD;②AB=CD;③∠A=∠C;④∠B=∠C.能使四边形ABCD为平行四边形的条件的序号是_______.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为点O,E,F,G,H分别为边AD,AB,BC,CD的中点,若AC=8,BD=6,则四边形EFGH的面积为_______.
15.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB′=60°,则矩形ABCD的面积是_______.
16.已知菱形ABCD的两条对角线长分别为6和8,M,N分别是边BC,
CD的中点,P是对角线BD上一点,则PM+PN的最小值是_______.
三、解答题(共52分)
17.(5分)如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的形状,并说明理由;
(2)连接EF,若AE=8
cm,∠A=60°,求线段EF的长.
18.(6分)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足
时,四边形AFBD是矩形;
(3)当△ABC满足
时,四边形AFBD是菱形.
19.(6分)如图,已知矩形ABCD中,AC与BD相交于O,DE平分∠ADC交BC于E,
∠BDE=15°,试求∠COE的度数.
20.(8分)如图,点E,F分别在ABCD的AD,BC边上,且AE=CF,AF交BE于点G,DF交CE于点H,
(1)求证:四边形BEDF是平行四边形;
(2)求证:EF与GH互相平分.
21.(8分)
如图,ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
(1)求证:四边形ABEF是矩形;
(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长.
22.(9分)(1)如图,D是△ABC的边BC上一点,且CD=AB,E,F分别是BD,AC的中点,G,H分别是AD,EF的中点,求证:GH⊥EF.
(2)若(1)中的∠ABC=90°,其它条件不变,求的值.
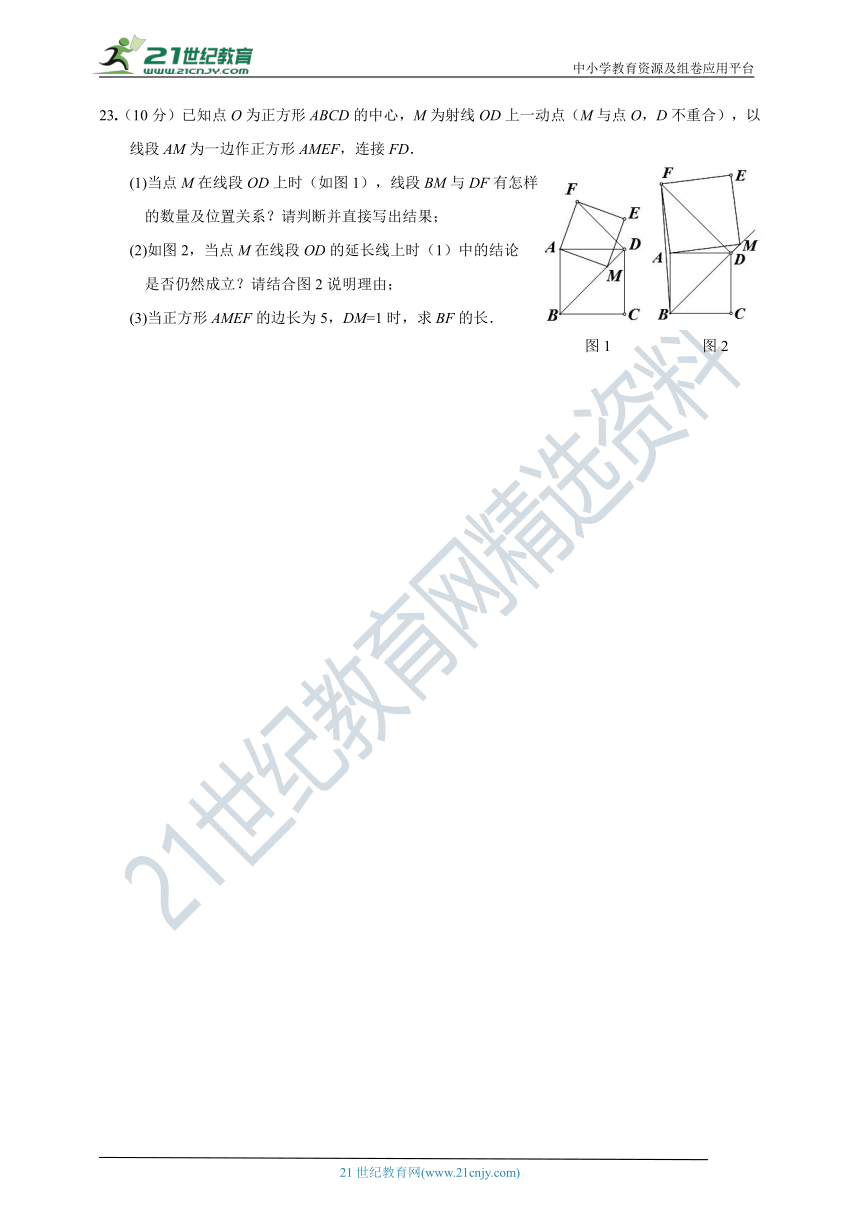
23.(10分)已知点O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以
线段AM为一边作正方形AMEF,连接FD.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样
的数量及位置关系?请判断并直接写出结果;
(2)如图2,当点M在线段OD的延长线上时(1)中的结论
是否仍然成立?请结合图2说明理由;
(3)当正方形AMEF的边长为5,DM=1时,求BF的长.
图1
图2
附加题(4+4+12=20分)
1、在正方形ABCD所在的平面内找一点P,使△PAB,△PBC,△PCD,△PDA
均为等腰三角形,符合条件的点有
个.
2、如图,已知,四边形ABCD中,AB=2,CD=3,M,N分别是AD,BC的中点,
则线段MN的取值范围是(
)
A.1<MN<5
?B.1<MN≤5
C.<MN<?
D.<MN≤?
3.如图,为所在平面内任意一点(不在直线上),
,为边中点.
操作:以为邻边作平行四边形,连结并延长到点,
使,连结.
探究:(1)请猜想与线段有关的三个结论;
(2)请你利用图a,图b选择不同位置的点按上述方法操作;
(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明;如果你认为你写的结论是错误的,请用图a或图b加以说明;(注意:错误的结论,只要你用反例给予说明也得分)
(4)若将“”改为“任意”,其他条件不变,利用图c操作,并写出与线段有
关的结论(直接写答案).
第18章答案
1-10
BDADA
CBCAB
11、8;12、22.5;13、①③④;14、24;15、16;16、5
(1)菱形,理由:根据题意得AE=AF=ED=DF,∴四边形AEDF是菱形
(2)∵AE=AF,∠A=60°,∴△EAF是等边三角形,∴EF=AE=8
cm
解:(1)BD=CD.
理由:∵AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,∠AFE=∠DCE,∠AEF=∠DEC,AE=DE,
∴△AEF≌△DEC
(AAS),∴AF=CD,
∵AF=BD,∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形;
(3)当△ABC满足:∠BAC=90°时,四边形AFBD是矩形.
19、解:∵四边形ABCD是矩形,DE平分∠ADC,
∴∠CDE=∠CED=
45°,∴EC=DC,
又∵∠BDE=15°,∴∠CDO=60°,
又∵矩形的对角线互相平分且相等,∴OD=OC,
∴△OCD是等边三角形,
∴∠DCO=60°,∠OCB=90°?∠DCO=30°,
∵DE平分∠ADC,∠ECD=90°,∠CDE=∠CED=
45°,
∴CD=CE=CO,∴∠COE=∠CEO;
∴∠COE=(180°-30°)÷2=75°.
∴EF与GH互相平分.
20、(1)略证:∵BF=DE,且BF∥DE,∴四边形BEDF是平行四边形;
(2)同理可证四边形AFCE是平行四边形;
∴BE∥DF,AF∥CE,
∴四边形EGFH是平行四边形,
21、(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DF=CE,∴DF+DE=CE+DE,
即FE=CD,∴FE=AB,
又AB∥FE,∴四边形ABEF是平行四边形.
∵BE⊥CD,∴∠BEF=90°,
∴四边形ABEF是矩形.
(2)由(1)知四边形ABEF是矩形,∴EF=AB=6,
∵DE=2,∴DF=CE=4,∴CF=10.
在Rt△ADF中,∠ADF=45°,∴AF=DF=4,
在Rt△ACF中,由勾股定理,得AC=2,
∵四边形ABCD是平行四边形,∴OA=OC,∴OF=AC=.
22、(1)连接EF,FG,
∵E,G分别是BD,AD的中点,
∴EG=AB,同理,FG=CD,
∵CD=AB,
∴EG=FG,
∵H是EF的中点,
∴GH⊥EF.
(2)∵E,G分别是BD,AD的中点,
∴EG∥AB,同理FG∥CD,
又∠ABC=90°,
∴∠EGF=90°,
∵H是EF的中点,
∴GH=EF,
∴
23、(1)DF=BM且DF⊥BM;
(2)△ABM
≌△ADF可证;
(3)作AG⊥BD于G,当点M在线段OD的延长线上时,可求得AG=3,进而求得BF=,
当点M在线段OD的延长线上时,可求得AG=3,进而求得BF=.
附加题答案:1、5;2、C
3、解:(1),.
(2)如图1,如图2.
(3)方法一:
如图3,连结,
,
.
.
.
,
四边形是平行四边形.
.
.
方法二:
如图4,连结,
,
四边形是平行四边形.
.
余下部分同方法一.
如图5,连结,交于,连结,
.
,
.
又,
,.
.
,..
(4)如图6,,.
第3题图
C
D
B
E
M
A
P
M
A
C
B
B
C
M
A
C
B
M
A
图c
图a
图b
C
D
A
P
M
E
B
图2
C
D
B
E
M
A
P
图1
C
D
B
E
M
A
P
P
图3
C
D
B
E
M
A
P
P
图4
C
D
B
E
M
A
P
P
图5
N
C
D
B
E
方法三:
M
A
P
P
图6
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第十八章平行四边形单元达标+培优检测题
(时间:100分钟 满分:100+20分)
一、选择题(每小题3分,共30分)
1.若平行四边形中两个内角的度数比为1∶3,则其中较小的内角是( )
A.
30°
B.45°
C.60°
D.75°
2.如图,已知四边形ABCD是平行四边形,对角线AC,BD相交于点O,
E是BC的中点,以下说法错误的是( )
A.OE=DC
B.OA=OC
C.∠BOE=∠OBA
D.∠OBE=∠OCE
3.如图,矩形ABCD的对角线AC=8
cm,∠AOD=120°,则AD的长为( )
A.4
cm
B.6
cm
C.3
cm
D.5
cm
4.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
5.下列说法正确的有( )
①有一个角是直角的平行四边形是矩形
②
四个角都相等的四边形是矩形
③两条对角线相等的四边形是矩形
④有一组对边相等,一组对角是直角的四边形是矩形
A.4个
B.3个
C.2个
D.1个
6.如图,已知点E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )
A.20°
B.25°
C.30°
D.35°
7.在ABCD中,AB=3,BC=4,当ABCD的面积最大时,下结论错误的是( )
A.AC=5
B.∠A+∠C=180°
C.AC⊥BD
D.AC=BD.
8.红丝带是关注艾滋病防治问题的国际性标志,人们将红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,如图所示.红丝带重叠部分形成的图形是( )
A、正方形
B、等腰梯形
C、菱形
D、矩形
第6题图
第8题图
第9题图
第10题图
9.如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE:∠BAE=1:2,则∠CAE的度数为(
)
A.
30°
B.
40°
C.45°
D.
50°
10.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上点M处,延长BC,EF交于点N,有下列四个结论:①DF=CF;
②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF,其中正确的结论是( )
A.①②③
B.①②④
C.②③④
D.①②③④
二、填空题(每小题3分,共18分)
11.如图,在ABCD中,AB=5,AC=6,当BD=_______时,四边形ABCD是菱形.
12.如图,正方形ABCD中,E是对角线BD上一点,且BE=BC,则∠DCE的度数是_______度.
第11题图
第12题图
第14题图
第15题图
13.在四边形ABCD中,AD∥BC,分别添加下列条件之一:①AB∥CD;②AB=CD;③∠A=∠C;④∠B=∠C.能使四边形ABCD为平行四边形的条件的序号是_______.
14.如图,在四边形ABCD中,对角线AC⊥BD,垂足为点O,E,F,G,H分别为边AD,AB,BC,CD的中点,若AC=8,BD=6,则四边形EFGH的面积为_______.
15.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB′=60°,则矩形ABCD的面积是_______.
16.已知菱形ABCD的两条对角线长分别为6和8,M,N分别是边BC,
CD的中点,P是对角线BD上一点,则PM+PN的最小值是_______.
三、解答题(共52分)
17.(5分)如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的形状,并说明理由;
(2)连接EF,若AE=8
cm,∠A=60°,求线段EF的长.
18.(6分)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足
时,四边形AFBD是矩形;
(3)当△ABC满足
时,四边形AFBD是菱形.
19.(6分)如图,已知矩形ABCD中,AC与BD相交于O,DE平分∠ADC交BC于E,
∠BDE=15°,试求∠COE的度数.
20.(8分)如图,点E,F分别在ABCD的AD,BC边上,且AE=CF,AF交BE于点G,DF交CE于点H,
(1)求证:四边形BEDF是平行四边形;
(2)求证:EF与GH互相平分.
21.(8分)
如图,ABCD中,对角线AC,BD交于点O,过点B作BE⊥CD于点E,延长CD到点F,使DF=CE,连接AF.
(1)求证:四边形ABEF是矩形;
(2)连接OF,若AB=6,DE=2,∠ADF=45°,求OF的长.
22.(9分)(1)如图,D是△ABC的边BC上一点,且CD=AB,E,F分别是BD,AC的中点,G,H分别是AD,EF的中点,求证:GH⊥EF.
(2)若(1)中的∠ABC=90°,其它条件不变,求的值.
23.(10分)已知点O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以
线段AM为一边作正方形AMEF,连接FD.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样
的数量及位置关系?请判断并直接写出结果;
(2)如图2,当点M在线段OD的延长线上时(1)中的结论
是否仍然成立?请结合图2说明理由;
(3)当正方形AMEF的边长为5,DM=1时,求BF的长.
图1
图2
附加题(4+4+12=20分)
1、在正方形ABCD所在的平面内找一点P,使△PAB,△PBC,△PCD,△PDA
均为等腰三角形,符合条件的点有
个.
2、如图,已知,四边形ABCD中,AB=2,CD=3,M,N分别是AD,BC的中点,
则线段MN的取值范围是(
)
A.1<MN<5
?B.1<MN≤5
C.<MN<?
D.<MN≤?
3.如图,为所在平面内任意一点(不在直线上),
,为边中点.
操作:以为邻边作平行四边形,连结并延长到点,
使,连结.
探究:(1)请猜想与线段有关的三个结论;
(2)请你利用图a,图b选择不同位置的点按上述方法操作;
(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明;如果你认为你写的结论是错误的,请用图a或图b加以说明;(注意:错误的结论,只要你用反例给予说明也得分)
(4)若将“”改为“任意”,其他条件不变,利用图c操作,并写出与线段有
关的结论(直接写答案).
第18章答案
1-10
BDADA
CBCAB
11、8;12、22.5;13、①③④;14、24;15、16;16、5
(1)菱形,理由:根据题意得AE=AF=ED=DF,∴四边形AEDF是菱形
(2)∵AE=AF,∠A=60°,∴△EAF是等边三角形,∴EF=AE=8
cm
解:(1)BD=CD.
理由:∵AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,∠AFE=∠DCE,∠AEF=∠DEC,AE=DE,
∴△AEF≌△DEC
(AAS),∴AF=CD,
∵AF=BD,∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形;
(3)当△ABC满足:∠BAC=90°时,四边形AFBD是矩形.
19、解:∵四边形ABCD是矩形,DE平分∠ADC,
∴∠CDE=∠CED=
45°,∴EC=DC,
又∵∠BDE=15°,∴∠CDO=60°,
又∵矩形的对角线互相平分且相等,∴OD=OC,
∴△OCD是等边三角形,
∴∠DCO=60°,∠OCB=90°?∠DCO=30°,
∵DE平分∠ADC,∠ECD=90°,∠CDE=∠CED=
45°,
∴CD=CE=CO,∴∠COE=∠CEO;
∴∠COE=(180°-30°)÷2=75°.
∴EF与GH互相平分.
20、(1)略证:∵BF=DE,且BF∥DE,∴四边形BEDF是平行四边形;
(2)同理可证四边形AFCE是平行四边形;
∴BE∥DF,AF∥CE,
∴四边形EGFH是平行四边形,
21、(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DF=CE,∴DF+DE=CE+DE,
即FE=CD,∴FE=AB,
又AB∥FE,∴四边形ABEF是平行四边形.
∵BE⊥CD,∴∠BEF=90°,
∴四边形ABEF是矩形.
(2)由(1)知四边形ABEF是矩形,∴EF=AB=6,
∵DE=2,∴DF=CE=4,∴CF=10.
在Rt△ADF中,∠ADF=45°,∴AF=DF=4,
在Rt△ACF中,由勾股定理,得AC=2,
∵四边形ABCD是平行四边形,∴OA=OC,∴OF=AC=.
22、(1)连接EF,FG,
∵E,G分别是BD,AD的中点,
∴EG=AB,同理,FG=CD,
∵CD=AB,
∴EG=FG,
∵H是EF的中点,
∴GH⊥EF.
(2)∵E,G分别是BD,AD的中点,
∴EG∥AB,同理FG∥CD,
又∠ABC=90°,
∴∠EGF=90°,
∵H是EF的中点,
∴GH=EF,
∴
23、(1)DF=BM且DF⊥BM;
(2)△ABM
≌△ADF可证;
(3)作AG⊥BD于G,当点M在线段OD的延长线上时,可求得AG=3,进而求得BF=,
当点M在线段OD的延长线上时,可求得AG=3,进而求得BF=.
附加题答案:1、5;2、C
3、解:(1),.
(2)如图1,如图2.
(3)方法一:
如图3,连结,
,
.
.
.
,
四边形是平行四边形.
.
.
方法二:
如图4,连结,
,
四边形是平行四边形.
.
余下部分同方法一.
如图5,连结,交于,连结,
.
,
.
又,
,.
.
,..
(4)如图6,,.
第3题图
C
D
B
E
M
A
P
M
A
C
B
B
C
M
A
C
B
M
A
图c
图a
图b
C
D
A
P
M
E
B
图2
C
D
B
E
M
A
P
图1
C
D
B
E
M
A
P
P
图3
C
D
B
E
M
A
P
P
图4
C
D
B
E
M
A
P
P
图5
N
C
D
B
E
方法三:
M
A
P
P
图6
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
