七年级数学7.2.1三角形的内角
文档属性
| 名称 | 七年级数学7.2.1三角形的内角 |

|
|
| 格式 | zip | ||
| 文件大小 | 219.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-20 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
第七章 三角形
7.2.1 三角形的内角
重庆市开县西街中学 罗堂喜
7.2 与三角形有关的角
三角形蓝和三角形红见面了,蓝炫耀的说:“我的面积比你大,所以我的内角和也比你大!”红不服气的说:“那可不好说噢,你自己量量看!”
蓝用量角器量了量自己和红,就不再说话了!
创设情境
(一)动手操作,引入新知
【问题1】我们已经知道,任意一个三角形的三个内角和等于180°.那么怎样证明这个结论呢?
方法一:通过具体的度量,验证三角形的内角和为180°.
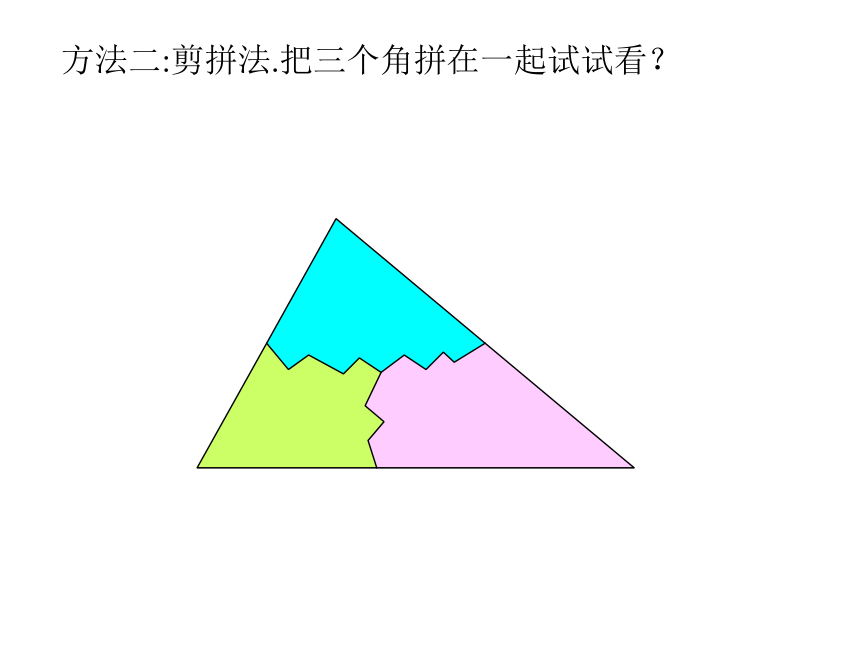
方法二:剪拼法.把三个角拼在一起试试看?
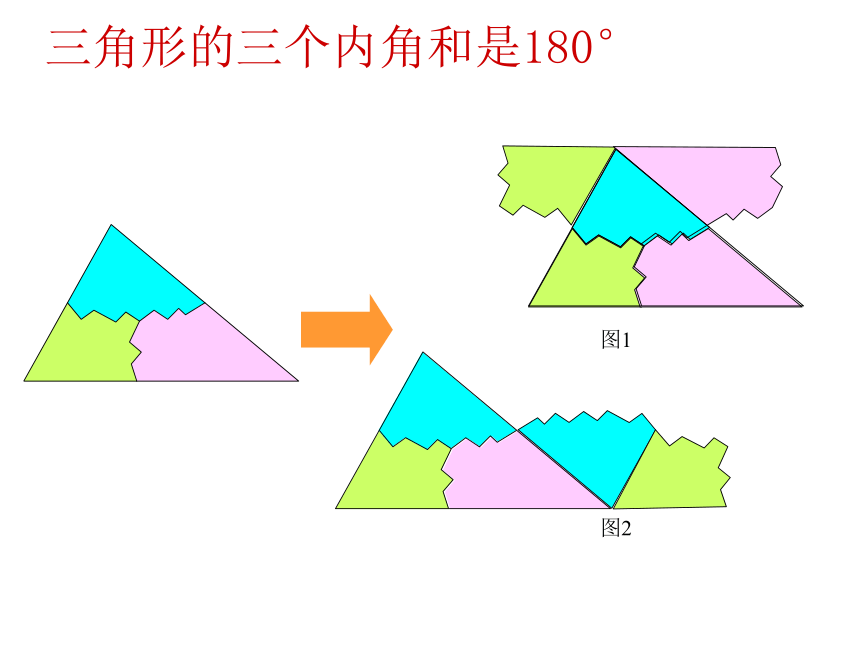
三角形的三个内角和是180°
图1
图2
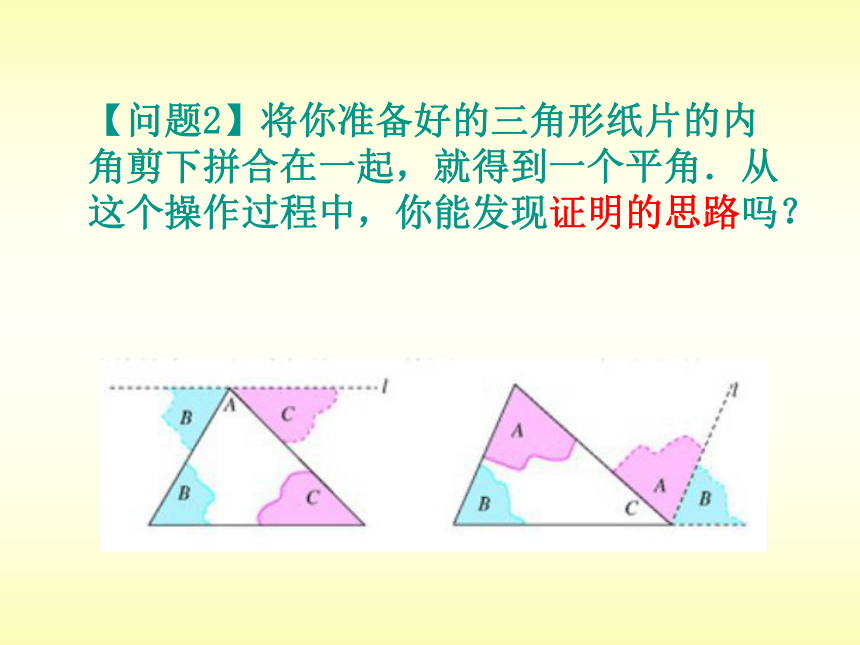
【问题2】将你准备好的三角形纸片的内角剪下拼合在一起,就得到一个平角.从这个操作过程中,你能发现证明的思路吗?
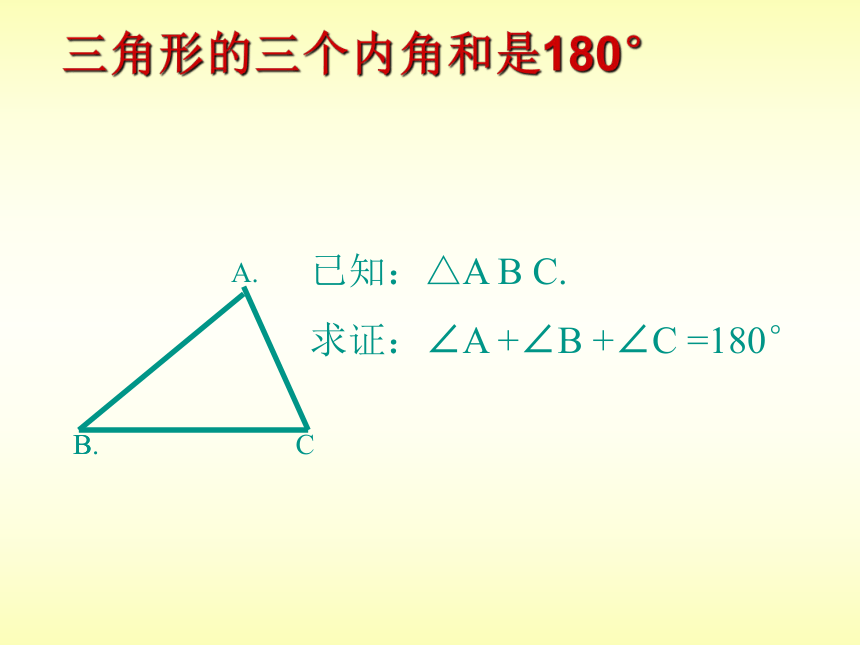
三角形的三个内角和是180°
已知:△A B C.
求证:∠A +∠B +∠C =180°
A.
B
C
B.
F
2
1
E
C
B
A
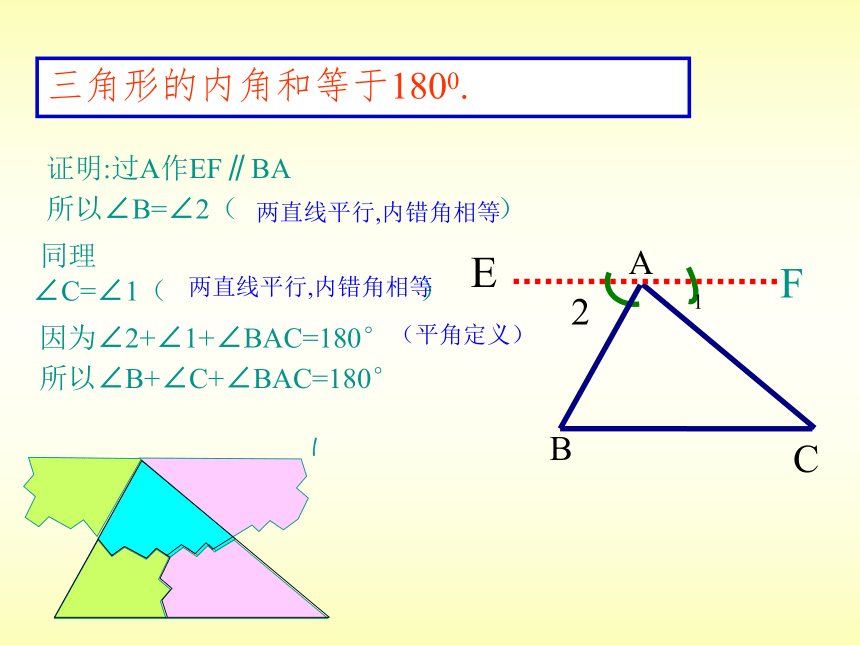
三角形的内角和等于1800.
证明:过A作EF∥BA
所以∠B=∠2( )
同理
∠C=∠1( )
因为∠2+∠1+∠BAC=180°
所以∠B+∠C+∠BAC=180°
(平角定义)
两直线平行,内错角相等
两直线平行,内错角相等
l
2
1
E
D
C
B
A
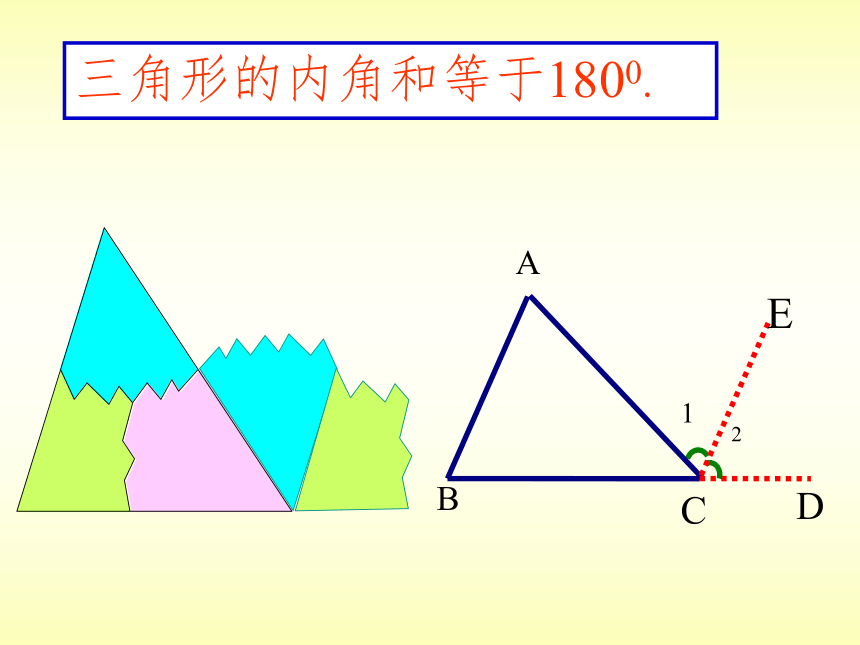
三角形的内角和等于1800.
C
B
E
A
三角形的内角和等于1800.
三角形三个内角的和等于180°.
三角形内角和定理:
(二)运用新知,解决问题
【思考】
(1)一个三角形最多有几个直角?为什么?
(2)一个三角形最多有几个钝角?为什么?
答案:(1)1个;(2)1个.
(1)在△ABC中,∠A=35°,
∠ B=43 ° , 则∠ C= .
(2) 在△ABC中,∠C=90°,∠B=50 ° , 则∠A=____。
(3)在△ABC中, ∠A=40 ° ∠A=2∠B,则∠C=____。
比一比,赛一赛
102 °
40 °
120°
【例】如图,C岛在A岛的北偏东50°方向,
B岛在A岛的北偏东80°方向,C岛在B岛的
北偏西40°方向.从C岛看A,B两岛的视角
∠ACB是多少度?
动动脑:还有其他的解法吗?
第1题:求出图中x的值。
第2题:如图,从A处观测C处时仰角∠CAD=30 ,从B处观测C处时仰角为∠CBD=45 ,则
∠CBA是 度,从C处观测A,B两处时视角∠ACB是 度
第1题
第2题
X=
X=
随堂练习
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠E的度数.
当堂测试
E
C
D
A
B
1
2
(2010.荆州)一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M、N.那么∠CME+∠BNF是( )
A .150° B.180°
C.135° D.不能确定
A
(三)基础训练,拓展应用
【练习1】如图,从A处观测C 处时
仰角∠CAD =30°,从B处观测C 处
时仰角∠CBD =45° ,从C 处观测A,
B 两处时视角∠ACB是多少?
【练习2】如图,一种滑翔伞的形状是左
右对称的四边形 ABCD,其中∠A =150°,
∠B =∠D=40°,求∠C 的度数.
【拓展练习】 △ABC中,∠B =∠A+10°,
∠C =∠B+10°,求△ABC 的各内角的度数.
答案:∠A=50°,
∠B=60°,
∠C=70°.
回顾与小结
本节课里你学到了什么???
1、三角形内角和的定理:三角形三个内角的和等于180 °
2、通过思考、去探究、去总结三角形内角和的定理,并且证明方法不止一种。
3、探索到一个数学规律,最终还须证明;并且学会怎样有条理的表达。
4、三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角;
5、证明三角形三个内角的和等于180 °要转化为:平角等于180 °或两直线平行同旁内角和等于180 °。
辅助线的添加与作法
【作业】
必做题:书第76页第1、4、7、9题.
选做题:书第77页第7、9题至少用两种方
法作答.
第七章 三角形
7.2.1 三角形的内角
重庆市开县西街中学 罗堂喜
7.2 与三角形有关的角
三角形蓝和三角形红见面了,蓝炫耀的说:“我的面积比你大,所以我的内角和也比你大!”红不服气的说:“那可不好说噢,你自己量量看!”
蓝用量角器量了量自己和红,就不再说话了!
创设情境
(一)动手操作,引入新知
【问题1】我们已经知道,任意一个三角形的三个内角和等于180°.那么怎样证明这个结论呢?
方法一:通过具体的度量,验证三角形的内角和为180°.
方法二:剪拼法.把三个角拼在一起试试看?
三角形的三个内角和是180°
图1
图2
【问题2】将你准备好的三角形纸片的内角剪下拼合在一起,就得到一个平角.从这个操作过程中,你能发现证明的思路吗?
三角形的三个内角和是180°
已知:△A B C.
求证:∠A +∠B +∠C =180°
A.
B
C
B.
F
2
1
E
C
B
A
三角形的内角和等于1800.
证明:过A作EF∥BA
所以∠B=∠2( )
同理
∠C=∠1( )
因为∠2+∠1+∠BAC=180°
所以∠B+∠C+∠BAC=180°
(平角定义)
两直线平行,内错角相等
两直线平行,内错角相等
l
2
1
E
D
C
B
A
三角形的内角和等于1800.
C
B
E
A
三角形的内角和等于1800.
三角形三个内角的和等于180°.
三角形内角和定理:
(二)运用新知,解决问题
【思考】
(1)一个三角形最多有几个直角?为什么?
(2)一个三角形最多有几个钝角?为什么?
答案:(1)1个;(2)1个.
(1)在△ABC中,∠A=35°,
∠ B=43 ° , 则∠ C= .
(2) 在△ABC中,∠C=90°,∠B=50 ° , 则∠A=____。
(3)在△ABC中, ∠A=40 ° ∠A=2∠B,则∠C=____。
比一比,赛一赛
102 °
40 °
120°
【例】如图,C岛在A岛的北偏东50°方向,
B岛在A岛的北偏东80°方向,C岛在B岛的
北偏西40°方向.从C岛看A,B两岛的视角
∠ACB是多少度?
动动脑:还有其他的解法吗?
第1题:求出图中x的值。
第2题:如图,从A处观测C处时仰角∠CAD=30 ,从B处观测C处时仰角为∠CBD=45 ,则
∠CBA是 度,从C处观测A,B两处时视角∠ACB是 度
第1题
第2题
X=
X=
随堂练习
如图,AB//CD,∠ABD与∠BDC的平分线相交于点E,求∠E的度数.
当堂测试
E
C
D
A
B
1
2
(2010.荆州)一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M、N.那么∠CME+∠BNF是( )
A .150° B.180°
C.135° D.不能确定
A
(三)基础训练,拓展应用
【练习1】如图,从A处观测C 处时
仰角∠CAD =30°,从B处观测C 处
时仰角∠CBD =45° ,从C 处观测A,
B 两处时视角∠ACB是多少?
【练习2】如图,一种滑翔伞的形状是左
右对称的四边形 ABCD,其中∠A =150°,
∠B =∠D=40°,求∠C 的度数.
【拓展练习】 △ABC中,∠B =∠A+10°,
∠C =∠B+10°,求△ABC 的各内角的度数.
答案:∠A=50°,
∠B=60°,
∠C=70°.
回顾与小结
本节课里你学到了什么???
1、三角形内角和的定理:三角形三个内角的和等于180 °
2、通过思考、去探究、去总结三角形内角和的定理,并且证明方法不止一种。
3、探索到一个数学规律,最终还须证明;并且学会怎样有条理的表达。
4、三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角;
5、证明三角形三个内角的和等于180 °要转化为:平角等于180 °或两直线平行同旁内角和等于180 °。
辅助线的添加与作法
【作业】
必做题:书第76页第1、4、7、9题.
选做题:书第77页第7、9题至少用两种方
法作答.
