8.5.3 怎样判定三角形相似

(共12张PPT)
8.5.3 怎样判定三角形相似
泰安十四中
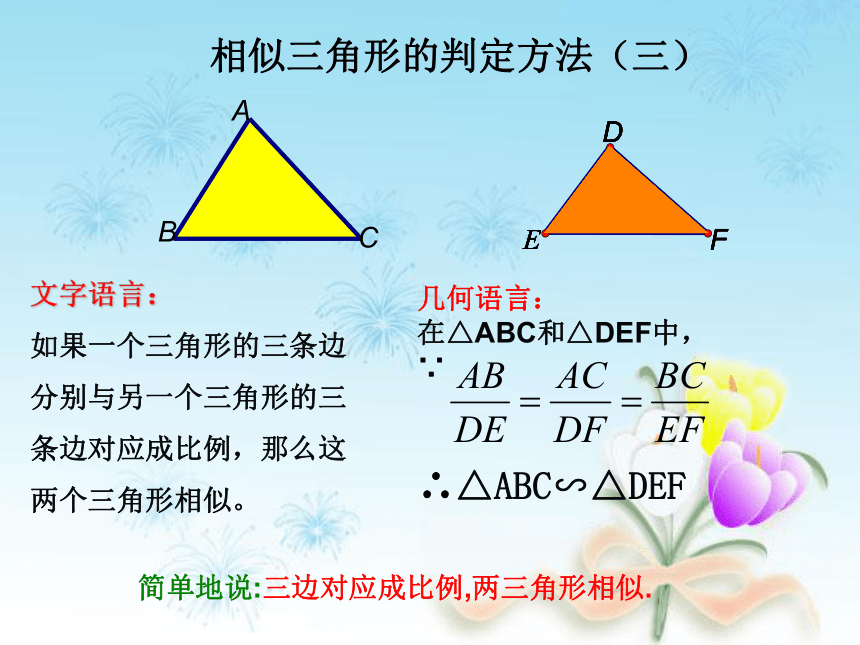
文字语言：
如果一个三角形的三条边
分别与另一个三角形的三
条边对应成比例，那么这
两个三角形相似。
几何语言：
在△ABC和△DEF中，
∵
∴△ABC∽△DEF
A
B
C
F
E
D
简单地说:三边对应成比例,两三角形相似.
相似三角形的判定方法（三）
F
E
D
F
E
D
F
E
D
F
E
D
学习目标
一、知识与技能
掌握两个三角形相似的判定方法。
二、过程与方法
.经历从实验探究到归纳结论的过程，发展合情的推理能力。 三、情感、态度与价值观
在探索解决问题中，发展合情观察力﹑分析力﹑运用所学知识解决问题能力。
应用新知
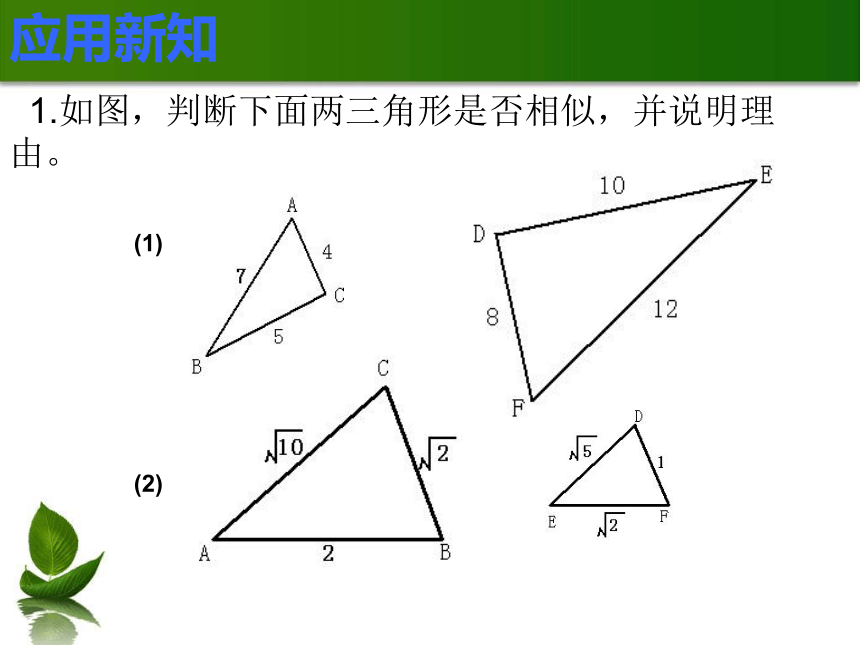
1.如图，判断下面两三角形是否相似，并说明理由。
(1)
(2)
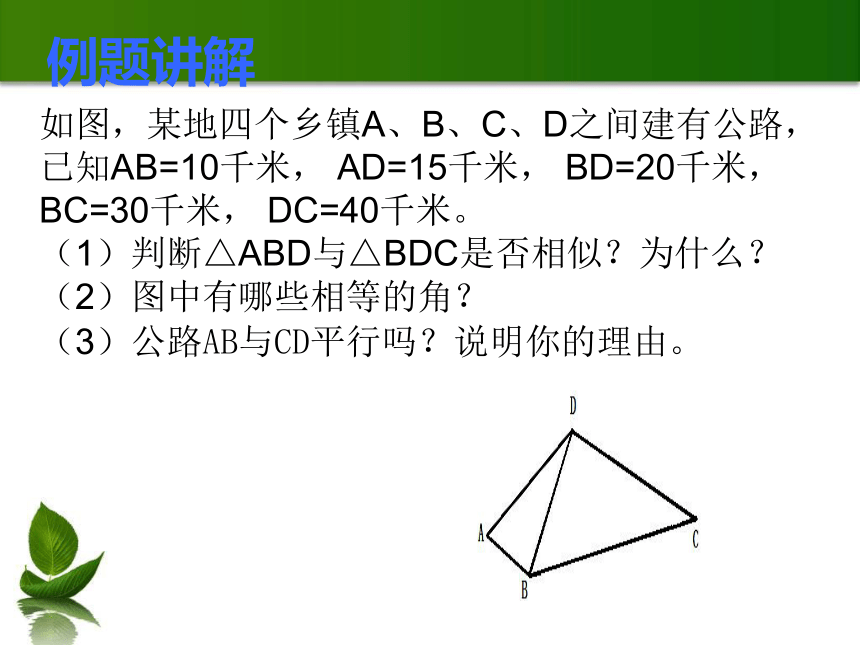
如图，某地四个乡镇A、B、C、D之间建有公路，已知AB=10千米， AD=15千米， BD=20千米， BC=30千米， DC=40千米。
（1）判断△ABD与△BDC是否相似？为什么？
（2）图中有哪些相等的角？
（3）公路AB与CD平行吗？说明你的理由。
例题讲解
应用新知
2.如图，在△ABC中，D，E分别在AB、AC上，AD=2，BD=4，AE=3，CE=6，DE=4，BC=12，试问△ADE与△ABC相似吗？为什么？
已知，如图所标示的数据，你能得出图中的相似三角形吗？
课堂小结
通过本堂课的学习
我学会了… …
我体会到… …
当堂达标
1、如图，方格纸上的每个小正方形的边长都为1，下列图中的三角形与右图中的△ABC相似的是( )。
2、如图，在四边形ABCD中，AB=2，BC=3，CD=6，AC=4，DA=8.AC平分∠BAD吗？为什么？
3、如图所示，
AB=3,AE=2,BE=4,ED=12,EC=6,CD=9
求证：△ABE∽△CDE
必做题：1、修改本节课过程不完善的题目。
2、课本46页 第1题 、第2题
选做题： 配套练习册 P18 第6题
作 业