七年级数学与三角形有关的角
文档属性
| 名称 | 七年级数学与三角形有关的角 |

|
|
| 格式 | zip | ||
| 文件大小 | 191.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-20 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
七年级数学(下)
荣县长山镇初级中学校 吴永
问题情境
我的面积比你大,我的内角和也一定比你的大
那可不一定哟,你自己用量角器量一量,看看什么结果?
命题:三角形的三个内角的和是180°
你能验证这个命题吗?
大胆猜测
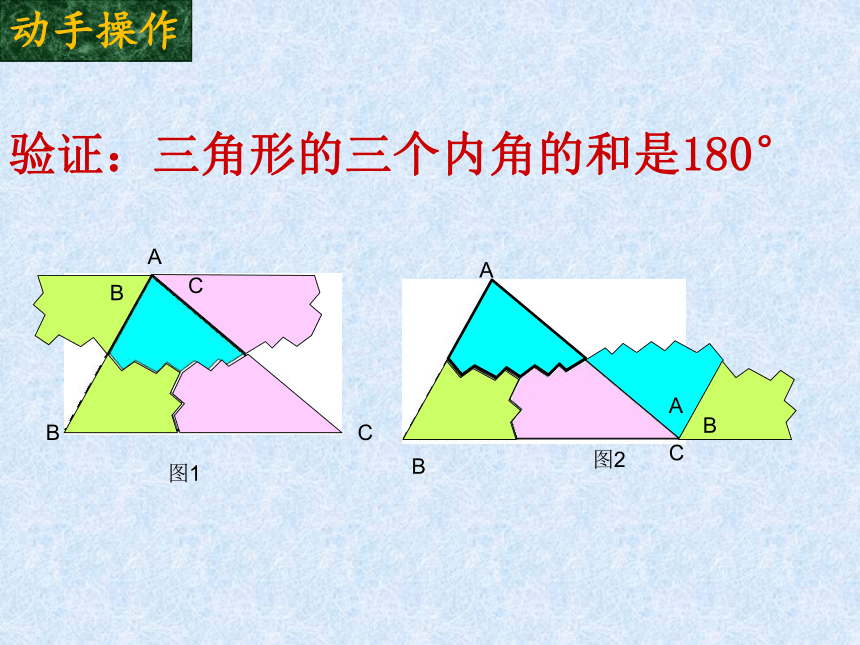
验证:三角形的三个内角的和是180°
图1
图2
A
B
C
C
B
A
B
C
A
B
动手操作
A
B
C
C
B
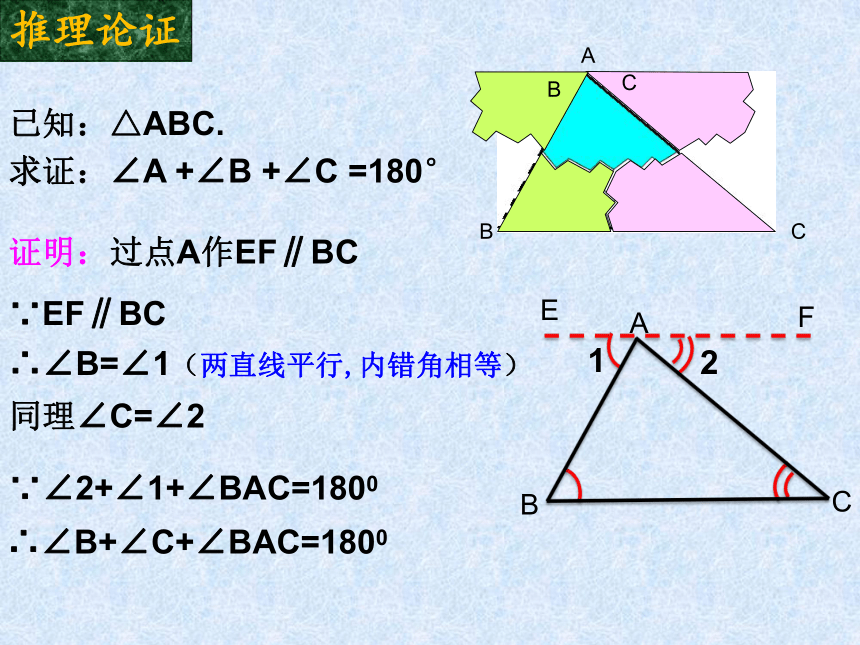
已知:△ABC.
求证:∠A +∠B +∠C =180°
E
F
证明:过点A作EF∥BC
∴∠B=∠1(两直线平行,内错角相等)
同理∠C=∠2
∵∠2+∠1+∠BAC=1800
∴∠B+∠C+∠BAC=1800
2
1
推理论证
A
B
C
∵EF∥BC
A
B
C
图2
A
B
C
A
B
D
E
推理论证
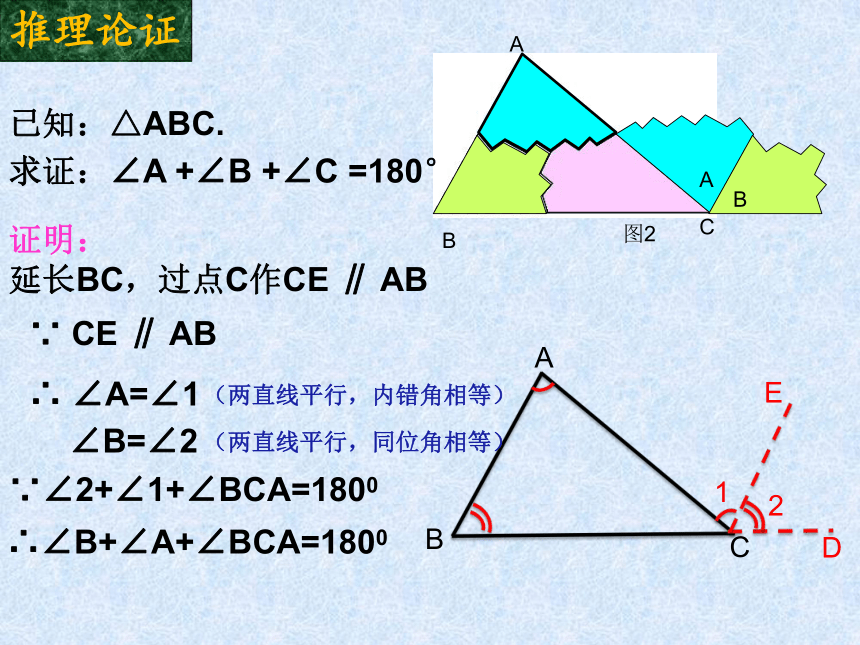
已知:△ABC.
求证:∠A +∠B +∠C =180°
证明:
延长BC,过点C作CE ∥ AB
∵ CE ∥ AB
∴ ∠A=∠1
2
1
∠B=∠2
(两直线平行,内错角相等)
(两直线平行,同位角相等)
∵∠2+∠1+∠BCA=1800
∴∠B+∠A+∠BCA=1800
推理论证
A
B
C
D
A
B
C
D
已知:△ABC.
求证:∠A +∠B +∠C =180°
分析:
过点A作AD∥BC
证明:(略)
归纳小结
命题:三角形的三个内角的和是180°
定理:三角形的三个内角的和是180°
推理
论
证
解答疑难几何图形问题时,在原图基础之上另外所作的具有极大价值的直线或者线段叫辅助线。作图时,画虚线,并且一条辅助线只能满足一个条件。
我们在证明三角形内角和定理的过程中,将三角形内角和问题转化熟悉的平角或两平行直线的同旁内角问题,用我们熟悉的知识、方法解决,这就是数学中常用的转化思想。
(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C= 。
(2)在△ABC中,∠C=90°,∠B=50°,
则∠A = ____。
(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ____。
小试身手
1020
400
1200
已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为
20°,60°,100°。
由三角形内角和为180°得
例题分析
课堂练习
(1)在△ABC中,∠A=75°,∠ B-∠ C=15°,
则∠ C= 。
(2)三角形的三个内角度数之比为2:3:5,
则这个三角形的三个内角的度数分别是:
45°
36°、 54°、90 °
归纳小结
定理:三角形的三个内角的和是180°
应用:
1、在三角形中,已知两个角的度数,可求另一个角的度数。
2、在三角形中,已知各角之间的数量关系,利用方程的思想,可求各角。
交流讨论
一个三角形中,最多有 个直角;
一个三角形中,最多有 个钝角;
一个三角形中,最少有 个锐角;
一个三角形中,最大的角不能小于 度。
1
1
2
60
七年级数学(下)
荣县长山镇初级中学校 吴永
问题情境
我的面积比你大,我的内角和也一定比你的大
那可不一定哟,你自己用量角器量一量,看看什么结果?
命题:三角形的三个内角的和是180°
你能验证这个命题吗?
大胆猜测
验证:三角形的三个内角的和是180°
图1
图2
A
B
C
C
B
A
B
C
A
B
动手操作
A
B
C
C
B
已知:△ABC.
求证:∠A +∠B +∠C =180°
E
F
证明:过点A作EF∥BC
∴∠B=∠1(两直线平行,内错角相等)
同理∠C=∠2
∵∠2+∠1+∠BAC=1800
∴∠B+∠C+∠BAC=1800
2
1
推理论证
A
B
C
∵EF∥BC
A
B
C
图2
A
B
C
A
B
D
E
推理论证
已知:△ABC.
求证:∠A +∠B +∠C =180°
证明:
延长BC,过点C作CE ∥ AB
∵ CE ∥ AB
∴ ∠A=∠1
2
1
∠B=∠2
(两直线平行,内错角相等)
(两直线平行,同位角相等)
∵∠2+∠1+∠BCA=1800
∴∠B+∠A+∠BCA=1800
推理论证
A
B
C
D
A
B
C
D
已知:△ABC.
求证:∠A +∠B +∠C =180°
分析:
过点A作AD∥BC
证明:(略)
归纳小结
命题:三角形的三个内角的和是180°
定理:三角形的三个内角的和是180°
推理
论
证
解答疑难几何图形问题时,在原图基础之上另外所作的具有极大价值的直线或者线段叫辅助线。作图时,画虚线,并且一条辅助线只能满足一个条件。
我们在证明三角形内角和定理的过程中,将三角形内角和问题转化熟悉的平角或两平行直线的同旁内角问题,用我们熟悉的知识、方法解决,这就是数学中常用的转化思想。
(1)在△ABC中,∠A=35°,∠ B=43°,
则∠ C= 。
(2)在△ABC中,∠C=90°,∠B=50°,
则∠A = ____。
(3)在△ABC中, ∠A=40°,∠A=2∠B,
则∠C = ____。
小试身手
1020
400
1200
已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、3x、5x,
x+3x+5x=180°
解得 x=20°
所以三个内角度数分别为
20°,60°,100°。
由三角形内角和为180°得
例题分析
课堂练习
(1)在△ABC中,∠A=75°,∠ B-∠ C=15°,
则∠ C= 。
(2)三角形的三个内角度数之比为2:3:5,
则这个三角形的三个内角的度数分别是:
45°
36°、 54°、90 °
归纳小结
定理:三角形的三个内角的和是180°
应用:
1、在三角形中,已知两个角的度数,可求另一个角的度数。
2、在三角形中,已知各角之间的数量关系,利用方程的思想,可求各角。
交流讨论
一个三角形中,最多有 个直角;
一个三角形中,最多有 个钝角;
一个三角形中,最少有 个锐角;
一个三角形中,最大的角不能小于 度。
1
1
2
60
