七年级数学7.2.2三角形的外角
文档属性
| 名称 | 七年级数学7.2.2三角形的外角 |

|
|
| 格式 | zip | ||
| 文件大小 | 1012.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-20 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
第七章 三角形
7.2.2 三角形的外角
重庆市开县西街中学 罗堂喜
7.2 与三角形有关的角
C
B
A
复习
【问题1】我们学习了三角形的内角定义
和内角和定理,你知道其内容吗?
C
B
A
开门见山,引入新知
如图,把△ABC的一边BC延长,得到
∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
【问题2】今天,让我们一起来探究
有关三角形外角的一些性质.那么什么
是外角呢?
D
以旧悟新,尝试发现
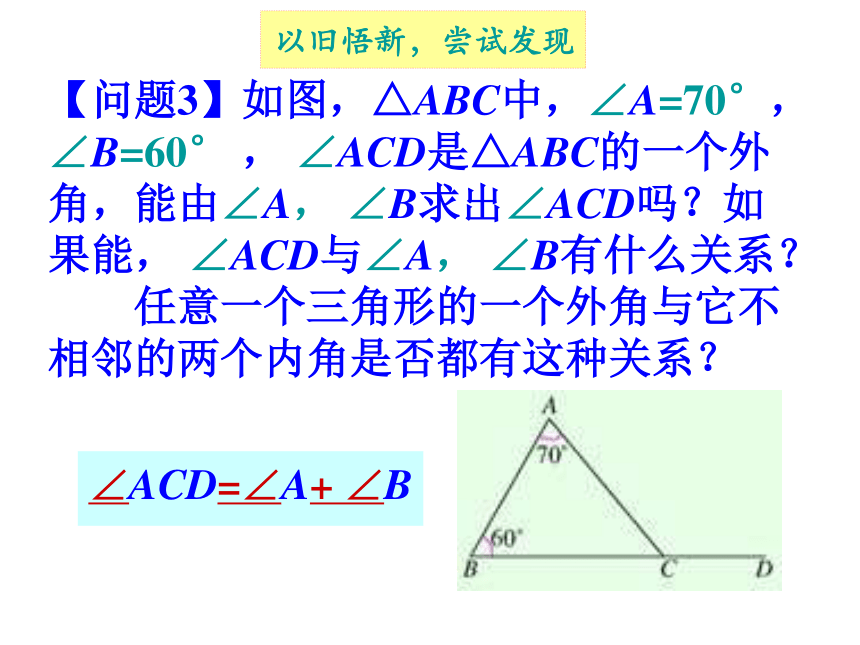
【问题3】如图,△ABC中,∠A=70°,
∠B=60° , ∠ACD是△ABC的一个外
角,能由∠A, ∠B求出∠ACD吗?如
果能, ∠ACD与∠A, ∠B有什么关系?
任意一个三角形的一个外角与它不
相邻的两个内角是否都有这种关系?
∠ACD=∠A+ ∠B
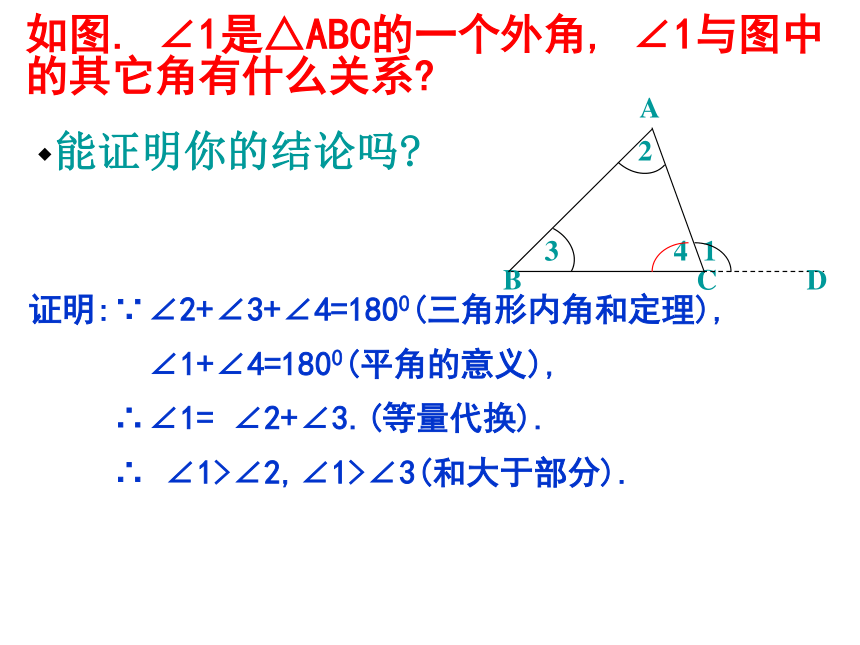
如图. ∠1是△ABC的一个外角, ∠1与图中的其它角有什么关系
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
A
B
C
D
1
2
3
4
能证明你的结论吗
以旧悟新,尝试发现
三角形外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任何一个内角.
应用举例,学以致用
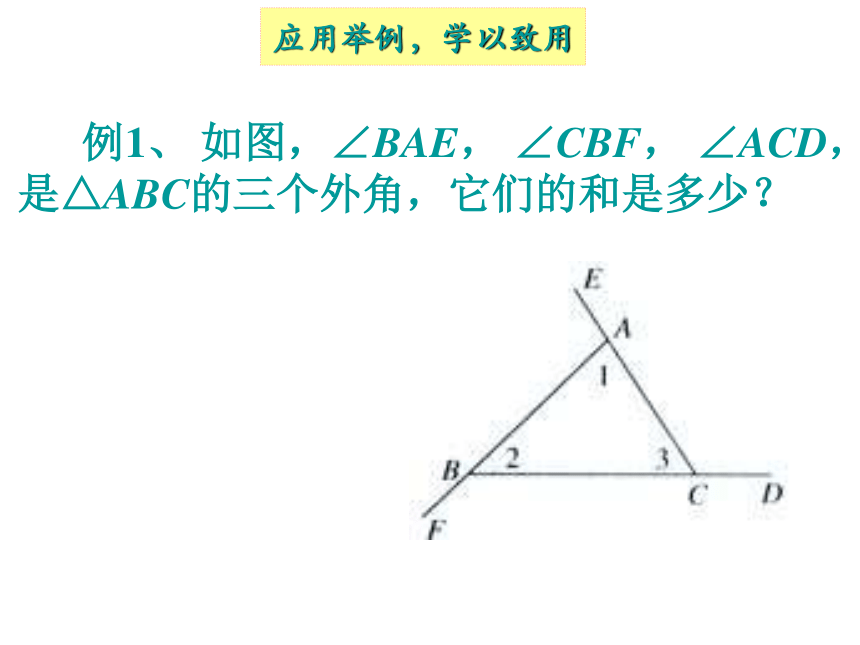
例1、 如图,∠BAE, ∠CBF, ∠ACD,
是△ABC的三个外角,它们的和是多少?
A
C
D
B
E
·
·
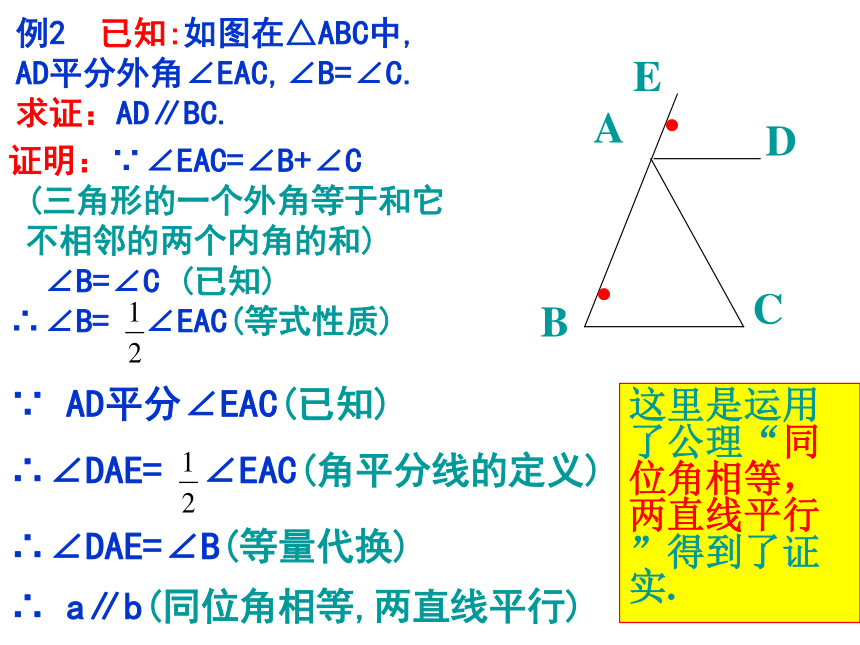
例2 已知:如图在△ABC中,
AD平分外角∠EAC,∠B=∠C.
求证:AD∥BC.
∵ AD平分∠EAC(已知)
∴∠DAE= ∠EAC(角平分线的定义)
∴∠DAE=∠B(等量代换)
∴ a∥b(同位角相等,两直线平行)
这里是运用了公理“同位角相等,两直线平行”得到了证实.
证明:∵∠EAC=∠B+∠C
(三角形的一个外角等于和它
不相邻的两个内角的和)
∠B=∠C (已知)
∴∠B= ∠EAC(等式性质)
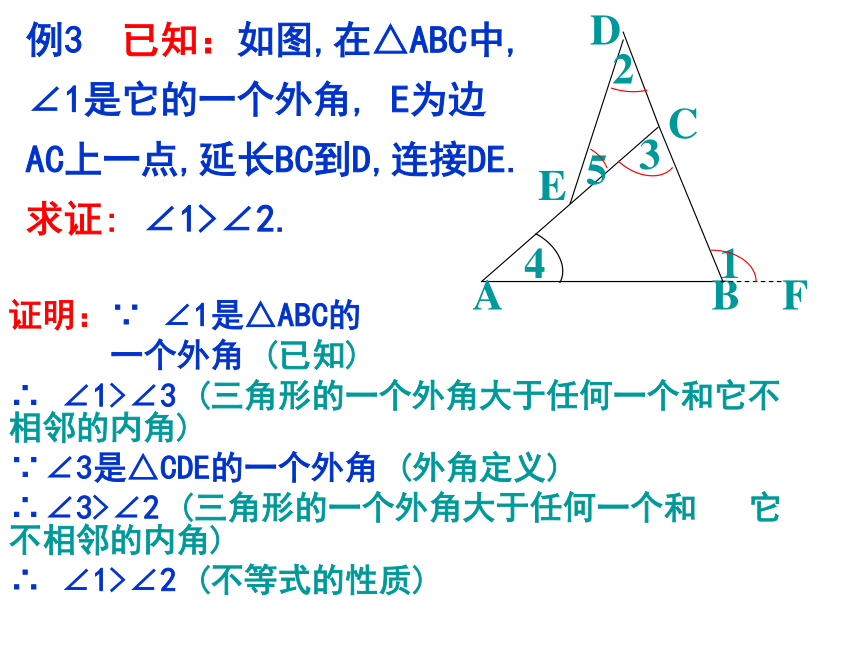
例3 已知:如图,在△ABC中,
∠1是它的一个外角, E为边
AC上一点,延长BC到D,连接DE.
求证: ∠1>∠2.
证明:∵ ∠1是△ABC的
一个外角 (已知)
∴ ∠1>∠3 (三角形的一个外角大于任何一个和它不相邻的内角)
∵∠3是△CDE的一个外角 (外角定义)
∴∠3>∠2 (三角形的一个外角大于任何一个和 它不相邻的内角)
∴ ∠1>∠2 (不等式的性质)
C
A
B
F
1
3
4
5
E
D
2
例4、已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个
外角(外角定义)
∴∠1=∠B+∠D(三角形的一个
外角等于和它不相邻的两个
内角的和)
又∵∠2是△EHC的一个外角(外角定义)
∴∠2=∠C+∠E(三角形的一个外角等于
和它不相邻的两个内角的和)
又∵∠A+∠1+∠2=180°(三角形内角和定理)
∴∠A+∠B+∠C+∠D+∠E =180°(等式性质)
A
B
C
D
E
F
1
H
2
如图,△ABE 和△ADC是△ABC 分别沿着
AB、AC 边翻折180°形成的.
若∠1:∠2:∠3=28:5:3 ,
则∠ɑ的度数为?
巩固练习
【练习1】如图,AB∥CD,∠A=45°
∠C= ∠E,求∠C .
拓展延伸,灵活运用
答案:22.5 °
【练习2】如图, CE是△ABC 的外角∠ACD
的平分线,且CE 交BA 的延长线于点E ,
证明∠BAC>∠B .
拓展延伸,灵活运用
E
D
C
B
A
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
1
2
3
4
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.
推论可以当作定理使用.
小结归纳
1
已知:如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:∵ ∠DCA是△ABC的一个外角(已知),
∠DCA=100°(已知),
∴ ∠B=100°-45°=55°.(三角形的一个外角等于和它不相邻的两个内角的和).
又∵ ∠DCA+∠BCA=180°(平角意义).
∴ ∠ACB=80°(等式的性质).
∠A=45°(已知),
行家伸伸手
已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
证明(2):∵ ∠BDC是△DCE的一个外角 (外角意义),
∴ ∠BDC =∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠DEC=∠A+ ∠B(三角形的一个外角等于和它不相邻的两个外角的和).
∴ ∠BDC=∠A+∠B+∠C (等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角意义),
B
C
A
D
E
关注三角形的外角
(2010.东营)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )
A. 50° B. 30°
C. 20° D. 15°
C
1
2
3
三角形内角和定理 :
推论1:
推论2:
推论3:
三角形三个内角的和等于1800.
三角形的一个外角等于和它不相邻
的两个内角的和.
三角形的一个外角大于任何一个和
它不相邻的内角.
直角三角形的两锐角互余.
小结归纳
2
总结归纳,布置作业
通过本节课的学习,你有什么收获?
作业:
书第75页练习,习题7.2第8题;
质量监测同步练习.
第七章 三角形
7.2.2 三角形的外角
重庆市开县西街中学 罗堂喜
7.2 与三角形有关的角
C
B
A
复习
【问题1】我们学习了三角形的内角定义
和内角和定理,你知道其内容吗?
C
B
A
开门见山,引入新知
如图,把△ABC的一边BC延长,得到
∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
【问题2】今天,让我们一起来探究
有关三角形外角的一些性质.那么什么
是外角呢?
D
以旧悟新,尝试发现
【问题3】如图,△ABC中,∠A=70°,
∠B=60° , ∠ACD是△ABC的一个外
角,能由∠A, ∠B求出∠ACD吗?如
果能, ∠ACD与∠A, ∠B有什么关系?
任意一个三角形的一个外角与它不
相邻的两个内角是否都有这种关系?
∠ACD=∠A+ ∠B
如图. ∠1是△ABC的一个外角, ∠1与图中的其它角有什么关系
证明:∵∠2+∠3+∠4=1800(三角形内角和定理),
∠1+∠4=1800(平角的意义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
A
B
C
D
1
2
3
4
能证明你的结论吗
以旧悟新,尝试发现
三角形外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任何一个内角.
应用举例,学以致用
例1、 如图,∠BAE, ∠CBF, ∠ACD,
是△ABC的三个外角,它们的和是多少?
A
C
D
B
E
·
·
例2 已知:如图在△ABC中,
AD平分外角∠EAC,∠B=∠C.
求证:AD∥BC.
∵ AD平分∠EAC(已知)
∴∠DAE= ∠EAC(角平分线的定义)
∴∠DAE=∠B(等量代换)
∴ a∥b(同位角相等,两直线平行)
这里是运用了公理“同位角相等,两直线平行”得到了证实.
证明:∵∠EAC=∠B+∠C
(三角形的一个外角等于和它
不相邻的两个内角的和)
∠B=∠C (已知)
∴∠B= ∠EAC(等式性质)
例3 已知:如图,在△ABC中,
∠1是它的一个外角, E为边
AC上一点,延长BC到D,连接DE.
求证: ∠1>∠2.
证明:∵ ∠1是△ABC的
一个外角 (已知)
∴ ∠1>∠3 (三角形的一个外角大于任何一个和它不相邻的内角)
∵∠3是△CDE的一个外角 (外角定义)
∴∠3>∠2 (三角形的一个外角大于任何一个和 它不相邻的内角)
∴ ∠1>∠2 (不等式的性质)
C
A
B
F
1
3
4
5
E
D
2
例4、已知:国旗上的正五角星形如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个
外角(外角定义)
∴∠1=∠B+∠D(三角形的一个
外角等于和它不相邻的两个
内角的和)
又∵∠2是△EHC的一个外角(外角定义)
∴∠2=∠C+∠E(三角形的一个外角等于
和它不相邻的两个内角的和)
又∵∠A+∠1+∠2=180°(三角形内角和定理)
∴∠A+∠B+∠C+∠D+∠E =180°(等式性质)
A
B
C
D
E
F
1
H
2
如图,△ABE 和△ADC是△ABC 分别沿着
AB、AC 边翻折180°形成的.
若∠1:∠2:∠3=28:5:3 ,
则∠ɑ的度数为?
巩固练习
【练习1】如图,AB∥CD,∠A=45°
∠C= ∠E,求∠C .
拓展延伸,灵活运用
答案:22.5 °
【练习2】如图, CE是△ABC 的外角∠ACD
的平分线,且CE 交BA 的延长线于点E ,
证明∠BAC>∠B .
拓展延伸,灵活运用
E
D
C
B
A
三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
1
2
3
4
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论.
推论可以当作定理使用.
小结归纳
1
已知:如图所示,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
A
B
C
D
解:∵ ∠DCA是△ABC的一个外角(已知),
∠DCA=100°(已知),
∴ ∠B=100°-45°=55°.(三角形的一个外角等于和它不相邻的两个内角的和).
又∵ ∠DCA+∠BCA=180°(平角意义).
∴ ∠ACB=80°(等式的性质).
∠A=45°(已知),
行家伸伸手
已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.
证明(2):∵ ∠BDC是△DCE的一个外角 (外角意义),
∴ ∠BDC =∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).
∴ ∠DEC=∠A+ ∠B(三角形的一个外角等于和它不相邻的两个外角的和).
∴ ∠BDC=∠A+∠B+∠C (等式的性质).
∵ ∠DEC是△ABE的一个外角 (外角意义),
B
C
A
D
E
关注三角形的外角
(2010.东营)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )
A. 50° B. 30°
C. 20° D. 15°
C
1
2
3
三角形内角和定理 :
推论1:
推论2:
推论3:
三角形三个内角的和等于1800.
三角形的一个外角等于和它不相邻
的两个内角的和.
三角形的一个外角大于任何一个和
它不相邻的内角.
直角三角形的两锐角互余.
小结归纳
2
总结归纳,布置作业
通过本节课的学习,你有什么收获?
作业:
书第75页练习,习题7.2第8题;
质量监测同步练习.
