4.5 利用三角形全等测距离 同步练习(含答案)
文档属性
| 名称 | 4.5 利用三角形全等测距离 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-16 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五节 利用三角形全等测距离同步练习
一、单选题
1.(2021·湖南长沙市·九年级专题练习)如图,乐乐书上的三角形墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是( )
A. B. C. D.
2.(2019·宜城市板桥店镇荩忱中学八年级期末)如图,,于,于,且,点从向运动,每分钟走1,点从向运动,每分钟走2,,两点同时出发,运动______分钟后与全等( )
A.4或6 B.4 C.6 D.5
3.(2020·河北保定市·八年级期末)如图,小强利用全等三角形的知识测量池塘两段M、N的距离.如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.线段OP
B.线段OQ
C.线段PQ
D.线段PN
4.(2020·沧州市第十三中学八年级月考)如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则下列结论:(1)AB=DE;(2)∠ABC+∠DFE=90°;(3)∠ABC=∠DEF中正确的有( )
A.1个 B.2个 C.3个 D.0个
5.(2020·武汉市第二十一(警予)中学八年级月考)如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.5 B.5或10 C.10 D.6或10
6.(2021·甘肃平凉市·八年级期末)如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使,连接BC并延长到点E,使,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到,理由是( )
A.SSS B.AAS C.ASA D.SAS
7.(2021·广东九年级专题练习)如图所示,将两根钢条AA’、BB’的中点O连在一起,使AA’、BB’可以绕着点O自由旋转,就做成了一个测量工件,则A’B’的长等于内槽宽AB,那么判定△OAB≌△OA’B’的理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
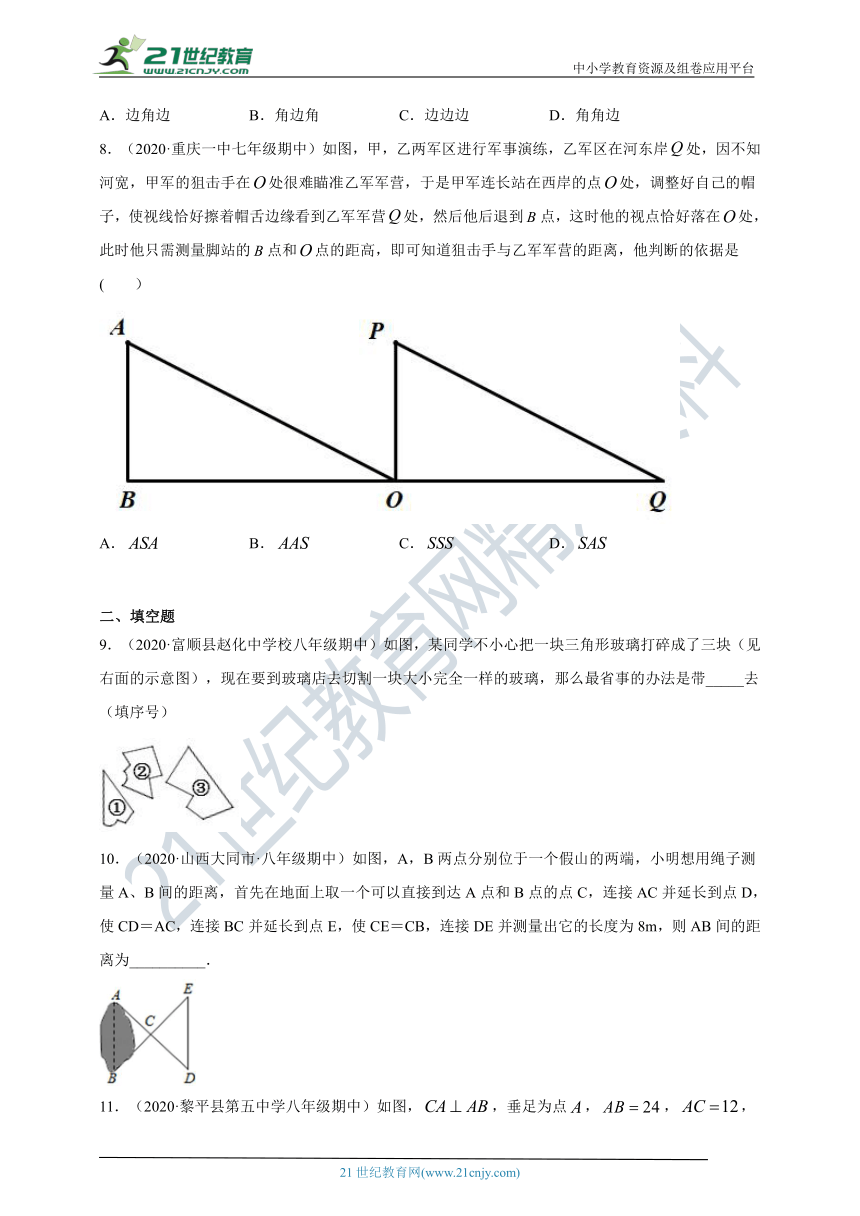
8.(2020·重庆一中七年级期中)如图,甲,乙两军区进行军事演练,乙军区在河东岸处,因不知河宽,甲军的狙击手在处很难瞄准乙军军营,于是甲军连长站在西岸的点处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到乙军军营处,然后他后退到点,这时他的视点恰好落在处,此时他只需测量脚站的点和点的距高,即可知道狙击手与乙军军营的距离,他判断的依据是( )
A. B. C. D.
二、填空题
9.(2020·富顺县赵化中学校八年级期中)如图,某同学不小心把一块三角形玻璃打碎成了三块(见右面的示意图),现在要到玻璃店去切割一块大小完全一样的玻璃,那么最省事的办法是带_____去(填序号)
10.(2020·山西大同市·八年级期中)如图,A,B两点分别位于一个假山的两端,小明想用绳子测量A、B间的距离,首先在地面上取一个可以直接到达A点和B点的点C,连接AC并延长到点D,使CD=AC,连接BC并延长到点E,使CE=CB,连接DE并测量出它的长度为8m,则AB间的距离为__________.
11.(2020·黎平县第五中学八年级期中)如图,,垂足为点,,,射线,垂足为点,一动点从点出发以3厘米秒沿射线运动,点为射线上一动点,随着点运动而运动,且始终保持,当点经过___秒时,与全等.
三、解答题
12.(2021·陕西九年级专题练习)如图,小叶和小丽两家分别位于A、B两处隔河相望,要测得两家之间的距离,请你设计出测量方案.
13.(2021·陕西九年级专题练习)如图为紫舞公园中的揽月湖,现在测量揽月湖两旁A、B两棵大树间的距离(不得直接量得).请你根据三角形全等的知识,用几根足够长的绳子及标杆为工具,设计一种测量方案.
要求:(1)画出设计的测量示意图;
(2)写出测量方案的理由.
14.(2021·湖北宜昌市·八年级期末)如图,、在一水池的两侧,为了测量水池的宽的长,现在水池外找一点,连接、并延长到、,使,,若测得,请求出水池的宽AB.
15.(2021·湖南怀化市·)明明同学用10块高度都是3cm的相同长方体小木块垒了两堵与地面垂直的木墙,木墙上面刚好可以放进一个等腰直角三角形(AC=BC ∠ACB=90°)点C在DE上,点A和点B分别与木墙的顶端重合,求两堵木墙之间的距离.
答案
一、单选题
1.B
2.B
3.C
4.C
5.A
6.D
7.A
8.B
二、填空题
9.③.
10.8m
11.0,4,12,16
三、解答题
12.【详解】
解:在点B所在的河岸上取点C,连结BC,使CD=CB,利用测角仪器使得∠B=∠D,且A、C、E三点在同一直线上,测量出DE的长,就是AB的长.
在△ABC和△ECD中
∴△ABC≌△ECD(ASA)
∴AB=DE.
13.【详解】
解:(1)如图所示;
分别以点A、点B为端点,作AQ、BP,
使其相交于点C,
使得CP=CB,CQ=CA,连接PQ,
测得PQ即可得出AB的长度.
(2)理由:由上面可知:PC=BC,QC=AC,
又∠PCQ=∠BCA,
∴在△PCQ与△BCA中,
∴△PCQ≌△BCA(SAS),
∴AB=PQ.
14.【详解】
解:如图,在△ACB和△DCE中,
∵ (SAS),
∴△ACB≌△DCE,
∴.
故答案为:10m.
15.【详解】
解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=9cm,DC=BE=21cm,
∴DE=DC+CE=30(cm),
答:两堵木墙之间的距离为30cm.
_21?????????è?????(www.21cnjy.com)_
第五节 利用三角形全等测距离同步练习
一、单选题
1.(2021·湖南长沙市·九年级专题练习)如图,乐乐书上的三角形墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是( )
A. B. C. D.
2.(2019·宜城市板桥店镇荩忱中学八年级期末)如图,,于,于,且,点从向运动,每分钟走1,点从向运动,每分钟走2,,两点同时出发,运动______分钟后与全等( )
A.4或6 B.4 C.6 D.5
3.(2020·河北保定市·八年级期末)如图,小强利用全等三角形的知识测量池塘两段M、N的距离.如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.线段OP
B.线段OQ
C.线段PQ
D.线段PN
4.(2020·沧州市第十三中学八年级月考)如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则下列结论:(1)AB=DE;(2)∠ABC+∠DFE=90°;(3)∠ABC=∠DEF中正确的有( )
A.1个 B.2个 C.3个 D.0个
5.(2020·武汉市第二十一(警予)中学八年级月考)如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.5 B.5或10 C.10 D.6或10
6.(2021·甘肃平凉市·八年级期末)如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使,连接BC并延长到点E,使,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到,理由是( )
A.SSS B.AAS C.ASA D.SAS
7.(2021·广东九年级专题练习)如图所示,将两根钢条AA’、BB’的中点O连在一起,使AA’、BB’可以绕着点O自由旋转,就做成了一个测量工件,则A’B’的长等于内槽宽AB,那么判定△OAB≌△OA’B’的理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
8.(2020·重庆一中七年级期中)如图,甲,乙两军区进行军事演练,乙军区在河东岸处,因不知河宽,甲军的狙击手在处很难瞄准乙军军营,于是甲军连长站在西岸的点处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到乙军军营处,然后他后退到点,这时他的视点恰好落在处,此时他只需测量脚站的点和点的距高,即可知道狙击手与乙军军营的距离,他判断的依据是( )
A. B. C. D.
二、填空题
9.(2020·富顺县赵化中学校八年级期中)如图,某同学不小心把一块三角形玻璃打碎成了三块(见右面的示意图),现在要到玻璃店去切割一块大小完全一样的玻璃,那么最省事的办法是带_____去(填序号)
10.(2020·山西大同市·八年级期中)如图,A,B两点分别位于一个假山的两端,小明想用绳子测量A、B间的距离,首先在地面上取一个可以直接到达A点和B点的点C,连接AC并延长到点D,使CD=AC,连接BC并延长到点E,使CE=CB,连接DE并测量出它的长度为8m,则AB间的距离为__________.
11.(2020·黎平县第五中学八年级期中)如图,,垂足为点,,,射线,垂足为点,一动点从点出发以3厘米秒沿射线运动,点为射线上一动点,随着点运动而运动,且始终保持,当点经过___秒时,与全等.
三、解答题
12.(2021·陕西九年级专题练习)如图,小叶和小丽两家分别位于A、B两处隔河相望,要测得两家之间的距离,请你设计出测量方案.
13.(2021·陕西九年级专题练习)如图为紫舞公园中的揽月湖,现在测量揽月湖两旁A、B两棵大树间的距离(不得直接量得).请你根据三角形全等的知识,用几根足够长的绳子及标杆为工具,设计一种测量方案.
要求:(1)画出设计的测量示意图;
(2)写出测量方案的理由.
14.(2021·湖北宜昌市·八年级期末)如图,、在一水池的两侧,为了测量水池的宽的长,现在水池外找一点,连接、并延长到、,使,,若测得,请求出水池的宽AB.
15.(2021·湖南怀化市·)明明同学用10块高度都是3cm的相同长方体小木块垒了两堵与地面垂直的木墙,木墙上面刚好可以放进一个等腰直角三角形(AC=BC ∠ACB=90°)点C在DE上,点A和点B分别与木墙的顶端重合,求两堵木墙之间的距离.
答案
一、单选题
1.B
2.B
3.C
4.C
5.A
6.D
7.A
8.B
二、填空题
9.③.
10.8m
11.0,4,12,16
三、解答题
12.【详解】
解:在点B所在的河岸上取点C,连结BC,使CD=CB,利用测角仪器使得∠B=∠D,且A、C、E三点在同一直线上,测量出DE的长,就是AB的长.
在△ABC和△ECD中
∴△ABC≌△ECD(ASA)
∴AB=DE.
13.【详解】
解:(1)如图所示;
分别以点A、点B为端点,作AQ、BP,
使其相交于点C,
使得CP=CB,CQ=CA,连接PQ,
测得PQ即可得出AB的长度.
(2)理由:由上面可知:PC=BC,QC=AC,
又∠PCQ=∠BCA,
∴在△PCQ与△BCA中,
∴△PCQ≌△BCA(SAS),
∴AB=PQ.
14.【详解】
解:如图,在△ACB和△DCE中,
∵ (SAS),
∴△ACB≌△DCE,
∴.
故答案为:10m.
15.【详解】
解:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS);
由题意得:AD=EC=9cm,DC=BE=21cm,
∴DE=DC+CE=30(cm),
答:两堵木墙之间的距离为30cm.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
