四川省成都外国语学校2012届高三3月月考(数学文理)
文档属性
| 名称 | 四川省成都外国语学校2012届高三3月月考(数学文理) |

|
|
| 格式 | zip | ||
| 文件大小 | 360.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-20 00:00:00 | ||
图片预览




文档简介
成都外国语学校高2012级第5次月考试题
数学试题(文、理科)
命题人:全 鑫 审题人:于开选
试题分第I卷和第Ⅱ卷两部分。满分150分,考试时间120 分钟。
注意事项:
1.答题前,务必将自己的姓名、考号准确无误地填写、填涂在答题卡规定的位置上;
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号;
3.答题时,必须使用黑色签字笔,将答案规范、整洁地书写在答题卡规定的位置上;[来源:21世纪教育网]
4.所有题目必须在答题卡上作答,在试题卷上答题无效;
5.考试结束后将答题卡交回,不得折叠、损毁答题卡。
第I卷
一、选择题(本大题共12小题,每小题5分,共60分,每小题只有一项是符合题目要求的)
1(文科)如果,那么( )
A. 0 B. C. D.
(理科)已知复数,则复数的虚部为( )
A . B. C. D.
2已知且,则角是( )
A.第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
3. 设m、n是两条不同的直线,是三个不同的平面,下列四个命题中正确的序号是( )
①//,则; ②;
③ ; ④.
A.①和② B.②和③ C.③和④ D.①和④
4.若,,则( )
A. B. C. D.
5.(文科)函数的反函数为( )
A. B.
C. D.
(理科)函数是连续函数,则( )[来源:21世纪教育网]
A 0 B 3 C -3 D 7 21世纪教育网
6.(文科)4名毕业生到两所不同的学校实习,每名毕业生只能选择一所学校实习,且每所学校至少有一名毕业生实习,其中甲、乙两名毕业生不能在同一所学校实习,则不同安排方法有( ) A. 12 B. 10 C. 8 D.6
(理科)已知,那么的取值范围是( )
A. B. 且 C. D. 或
7.已知函数的定义域为,,且,则满足条件的函数的个数为( )
A. 1 B. 1023 C. 1024 D.
8.已知点、分别是双曲线的左、右焦点,过且垂直于轴的直线与双曲线交于、两点,若为锐角三角形,则该双曲线的离心率的取值范围是
A. B. C.(1,2) D.
9如果数列对任意满足,且,那么( )
A.256 B.510 C.512 D. 1024
10.已知,直线交椭圆于A,B两点,的面积为(是坐标原点),则函数的奇偶性( )
A. 偶函数 B. 奇函数 C. 不是奇函数也不是偶函数 D. 奇偶性与有关
11.(文科)若实数满足,则( )
A.最小值为 B. 最大值为 C. 最大值为 D. 最小值为
(理科)设点如果直线与线段有一个公共点,那么 ( )
A.最大值为 B. 最大值为 C. 最小值为 D. 最小值为
12.设函数的定义域为,若存在非零实数使得对于任意,有,且,则称为上的高调函数,如果定义域为的函数是奇函数,当时,且函数为上的1高调函数,那么实数的取值范围为( )
A. B. C. D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答卷的横线上.
13.(文科) 已知函数的最小值为,则二项式的展开式中常数项为第 项。
(理科)已知,则_______
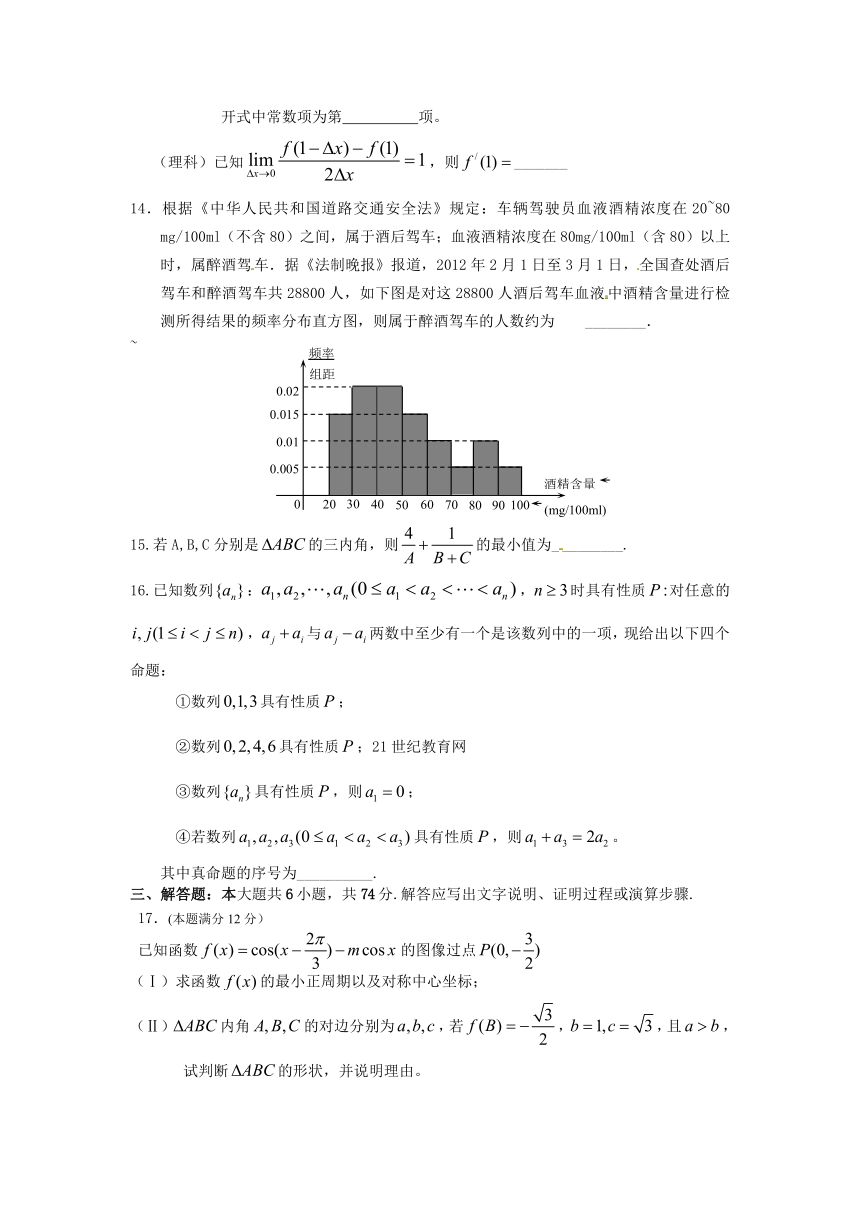
14.根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车;血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.据《法制晚报》报道,2012年2月1日至3月1日,全国查处酒后驾车和醉酒驾车共28800人,如下图是对这28800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为 ________.
~
15.若A,B,C分别是的三内角,则的最小值为_________.
16.已知数列:,时具有性质对任意的,与两数中至少有一个是该数列中的一项,现给出以下四个命题:
①数列具有性质;
②数列具有性质;21世纪教育网
③数列具有性质,则;
④若数列具有性质,则。
其中真命题的序号为__________.
三、解答题:本大題共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
已知函数的图像过点
(Ⅰ)求函数的最小正周期以及对称中心坐标;
(Ⅱ)内角的对边分别为,若,,且,
试判断的形状,并说明理由。
18.(本题满分12分)
某品牌专卖店准备在国庆期间举行促销活动,根据市场调查,该店决定从2种不同型号的洗衣机,2种不同型号的电视机和3种不同型号的空调中(不同种商品的型号不同),选出4种不同型号的商品进行促销,该店对选出的商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买任何一种型号的商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得元奖金.假设顾客每次抽奖时获奖与否的概率都是,
(Ⅰ)求选出的4种不同型号商品中,洗衣机、电视机、空调都至少有一种型号的概率;
(Ⅱ)(文科)若顾客购买两种不同型号的商品,求中奖奖金至少元的概率;
(理科)设顾客在三次抽奖中所获得的奖金总额(单位:元)为随机变量.请写出的分布列,并求的数学期望;
(Ⅲ)(理科)在(Ⅱ)的条件下,问该店若想采用此促销方案获利,则每次中奖奖金要低于多少元?
19.(本小题满分12分)
如图,在直三棱柱中,,,是的中点.21世纪教育网
(Ⅰ)求证:∥平面; (Ⅱ)求二面角的余弦值;
(Ⅲ)(理科)试问线段上是否存在点,使与成 角?若存在,确定点位置,若不存在,说明理由.
21世纪教育网
21世纪教育网
20. (本题满分12分)
已知数列中,,
(Ⅰ)求数列的通项公式;
(Ⅱ)求数列的前项和;
(Ⅲ)(理科)若存在,使得成立,求实数的最小值。
21.(本题满分12分)
已知焦点在轴上椭圆的长轴的端点分别为,为椭圆的中心,为右焦点,且,离心率。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)记椭圆的上顶点为,直线交椭圆于两点,问:是否存在直线,使点恰好为的垂心?若存在,求出直线的方程,若不存在,请说明理由。
22.(本题满分14分)
已知函数是定义在上的奇函数,且在处取得极小值。设表示的导函数,定义数列满足:
(Ⅰ)求数列的通项公式;
(Ⅱ)对任意,若,证明:;
(Ⅲ)(理科)试比较与的大小。
成都外国语学校高2012届三月月考试题数学试题参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12[来源:21世纪教育网]
答案 C B D A B C B D D A C理A文 B
填空题
13. 文科:9 理科 14. 4320 15. 16 . ②
三、解答题:
17(本小题满分12分)解:(Ⅰ)由有
从而,所以 对称中心
(Ⅱ)由(Ⅰ)有
所以,,又因为
所以,,即 由正弦定理:,得故:,(舍去)所以 所以为直角三角形
18:解:(本小题满分12分)
21世纪教育网
所以,顾客在三次抽奖中所获得的奖金总额的分布列为:21世纪教育网
0
……………9分
于是顾客在三次抽奖中所获得的奖金总额的数学期望是
. ………………10分
(文科)(Ⅰ)同理科
(Ⅱ)设事件B“若顾客购买两种不同型号的商品,中奖奖金至少元”
则
故:若顾客购买两种不同型号的商品,中奖奖金至少元的概率为。
19. .(本小题满分12分)
(Ⅰ)证明:连结,交于点,连结.
由 是直三棱柱,
得 四边形为矩形,为的中点.
又为中点,所以为中位线,
所以 ∥,
因为 平面,平面,
所以 ∥平面. ………………4分
(Ⅱ)解:由是直三棱柱,且,故两两垂直.
如图建立空间直角坐标系.
设,则.
所以 ,
设平面的法向量为,则有21世纪教育网
所以 取,得.
易知平面的法向量为.
由二面角是锐角,得 . ………………8分
所以二面角的余弦值为.
(Ⅲ)解:假设存在满足条件的点.
因为在线段上,,,故可设,其中.
所以 ,.
因为与成角,所以.
即,解得,舍去.
所以当点为线段中点时,与成角. ………………12分
20解:(Ⅰ)┄┄┄ ①
┄┄┄ ②
由①-②得:
所以是从第二项起首项为2,公比为3的等比数列,则:
(Ⅱ)由(Ⅰ)可知当时,
ⅰ当时,
ⅱ当时, ┄┄┄ ③
┄┄┄ ④
由③-④得:
又当时,满足上式
所以:
(Ⅲ)由等价于,由(Ⅰ)可知,当时,
设,则
所以, ,即
所以,又因为
所以, 实数的最小值为。
21解:(Ⅰ)略
(Ⅱ)假设存在直线交椭圆与点两点,且恰为的垂心,设,,因为,故。于是设直线为,由得
所以:,
又
即:
由韦达定理得:
解得或(舍去)
经检验符合条件,故直线的方程为。
22.解:(Ⅰ)
(Ⅱ)由(Ⅰ)知。因为(当时取等号)。又
(Ⅲ),构造函数,则上式等价于证成立,所以。又令,则当时成立,即得在上单调递减,于是成立,即成立,故成立。所以,由此知单调递减,所以,即,所以
版权所有:高考资源网(www.)
酒精含量
频率
组距
0.02
0.015
0.01
0.005
0
20
30
40
50
60
70
80
90
100
(mg/100ml)
数学试题(文、理科)
命题人:全 鑫 审题人:于开选
试题分第I卷和第Ⅱ卷两部分。满分150分,考试时间120 分钟。
注意事项:
1.答题前,务必将自己的姓名、考号准确无误地填写、填涂在答题卡规定的位置上;
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号;
3.答题时,必须使用黑色签字笔,将答案规范、整洁地书写在答题卡规定的位置上;[来源:21世纪教育网]
4.所有题目必须在答题卡上作答,在试题卷上答题无效;
5.考试结束后将答题卡交回,不得折叠、损毁答题卡。
第I卷
一、选择题(本大题共12小题,每小题5分,共60分,每小题只有一项是符合题目要求的)
1(文科)如果,那么( )
A. 0 B. C. D.
(理科)已知复数,则复数的虚部为( )
A . B. C. D.
2已知且,则角是( )
A.第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
3. 设m、n是两条不同的直线,是三个不同的平面,下列四个命题中正确的序号是( )
①//,则; ②;
③ ; ④.
A.①和② B.②和③ C.③和④ D.①和④
4.若,,则( )
A. B. C. D.
5.(文科)函数的反函数为( )
A. B.
C. D.
(理科)函数是连续函数,则( )[来源:21世纪教育网]
A 0 B 3 C -3 D 7 21世纪教育网
6.(文科)4名毕业生到两所不同的学校实习,每名毕业生只能选择一所学校实习,且每所学校至少有一名毕业生实习,其中甲、乙两名毕业生不能在同一所学校实习,则不同安排方法有( ) A. 12 B. 10 C. 8 D.6
(理科)已知,那么的取值范围是( )
A. B. 且 C. D. 或
7.已知函数的定义域为,,且,则满足条件的函数的个数为( )
A. 1 B. 1023 C. 1024 D.
8.已知点、分别是双曲线的左、右焦点,过且垂直于轴的直线与双曲线交于、两点,若为锐角三角形,则该双曲线的离心率的取值范围是
A. B. C.(1,2) D.
9如果数列对任意满足,且,那么( )
A.256 B.510 C.512 D. 1024
10.已知,直线交椭圆于A,B两点,的面积为(是坐标原点),则函数的奇偶性( )
A. 偶函数 B. 奇函数 C. 不是奇函数也不是偶函数 D. 奇偶性与有关
11.(文科)若实数满足,则( )
A.最小值为 B. 最大值为 C. 最大值为 D. 最小值为
(理科)设点如果直线与线段有一个公共点,那么 ( )
A.最大值为 B. 最大值为 C. 最小值为 D. 最小值为
12.设函数的定义域为,若存在非零实数使得对于任意,有,且,则称为上的高调函数,如果定义域为的函数是奇函数,当时,且函数为上的1高调函数,那么实数的取值范围为( )
A. B. C. D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答卷的横线上.
13.(文科) 已知函数的最小值为,则二项式的展开式中常数项为第 项。
(理科)已知,则_______
14.根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车;血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.据《法制晚报》报道,2012年2月1日至3月1日,全国查处酒后驾车和醉酒驾车共28800人,如下图是对这28800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为 ________.
~
15.若A,B,C分别是的三内角,则的最小值为_________.
16.已知数列:,时具有性质对任意的,与两数中至少有一个是该数列中的一项,现给出以下四个命题:
①数列具有性质;
②数列具有性质;21世纪教育网
③数列具有性质,则;
④若数列具有性质,则。
其中真命题的序号为__________.
三、解答题:本大題共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分12分)
已知函数的图像过点
(Ⅰ)求函数的最小正周期以及对称中心坐标;
(Ⅱ)内角的对边分别为,若,,且,
试判断的形状,并说明理由。
18.(本题满分12分)
某品牌专卖店准备在国庆期间举行促销活动,根据市场调查,该店决定从2种不同型号的洗衣机,2种不同型号的电视机和3种不同型号的空调中(不同种商品的型号不同),选出4种不同型号的商品进行促销,该店对选出的商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买任何一种型号的商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得元奖金.假设顾客每次抽奖时获奖与否的概率都是,
(Ⅰ)求选出的4种不同型号商品中,洗衣机、电视机、空调都至少有一种型号的概率;
(Ⅱ)(文科)若顾客购买两种不同型号的商品,求中奖奖金至少元的概率;
(理科)设顾客在三次抽奖中所获得的奖金总额(单位:元)为随机变量.请写出的分布列,并求的数学期望;
(Ⅲ)(理科)在(Ⅱ)的条件下,问该店若想采用此促销方案获利,则每次中奖奖金要低于多少元?
19.(本小题满分12分)
如图,在直三棱柱中,,,是的中点.21世纪教育网
(Ⅰ)求证:∥平面; (Ⅱ)求二面角的余弦值;
(Ⅲ)(理科)试问线段上是否存在点,使与成 角?若存在,确定点位置,若不存在,说明理由.
21世纪教育网
21世纪教育网
20. (本题满分12分)
已知数列中,,
(Ⅰ)求数列的通项公式;
(Ⅱ)求数列的前项和;
(Ⅲ)(理科)若存在,使得成立,求实数的最小值。
21.(本题满分12分)
已知焦点在轴上椭圆的长轴的端点分别为,为椭圆的中心,为右焦点,且,离心率。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)记椭圆的上顶点为,直线交椭圆于两点,问:是否存在直线,使点恰好为的垂心?若存在,求出直线的方程,若不存在,请说明理由。
22.(本题满分14分)
已知函数是定义在上的奇函数,且在处取得极小值。设表示的导函数,定义数列满足:
(Ⅰ)求数列的通项公式;
(Ⅱ)对任意,若,证明:;
(Ⅲ)(理科)试比较与的大小。
成都外国语学校高2012届三月月考试题数学试题参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12[来源:21世纪教育网]
答案 C B D A B C B D D A C理A文 B
填空题
13. 文科:9 理科 14. 4320 15. 16 . ②
三、解答题:
17(本小题满分12分)解:(Ⅰ)由有
从而,所以 对称中心
(Ⅱ)由(Ⅰ)有
所以,,又因为
所以,,即 由正弦定理:,得故:,(舍去)所以 所以为直角三角形
18:解:(本小题满分12分)
21世纪教育网
所以,顾客在三次抽奖中所获得的奖金总额的分布列为:21世纪教育网
0
……………9分
于是顾客在三次抽奖中所获得的奖金总额的数学期望是
. ………………10分
(文科)(Ⅰ)同理科
(Ⅱ)设事件B“若顾客购买两种不同型号的商品,中奖奖金至少元”
则
故:若顾客购买两种不同型号的商品,中奖奖金至少元的概率为。
19. .(本小题满分12分)
(Ⅰ)证明:连结,交于点,连结.
由 是直三棱柱,
得 四边形为矩形,为的中点.
又为中点,所以为中位线,
所以 ∥,
因为 平面,平面,
所以 ∥平面. ………………4分
(Ⅱ)解:由是直三棱柱,且,故两两垂直.
如图建立空间直角坐标系.
设,则.
所以 ,
设平面的法向量为,则有21世纪教育网
所以 取,得.
易知平面的法向量为.
由二面角是锐角,得 . ………………8分
所以二面角的余弦值为.
(Ⅲ)解:假设存在满足条件的点.
因为在线段上,,,故可设,其中.
所以 ,.
因为与成角,所以.
即,解得,舍去.
所以当点为线段中点时,与成角. ………………12分
20解:(Ⅰ)┄┄┄ ①
┄┄┄ ②
由①-②得:
所以是从第二项起首项为2,公比为3的等比数列,则:
(Ⅱ)由(Ⅰ)可知当时,
ⅰ当时,
ⅱ当时, ┄┄┄ ③
┄┄┄ ④
由③-④得:
又当时,满足上式
所以:
(Ⅲ)由等价于,由(Ⅰ)可知,当时,
设,则
所以, ,即
所以,又因为
所以, 实数的最小值为。
21解:(Ⅰ)略
(Ⅱ)假设存在直线交椭圆与点两点,且恰为的垂心,设,,因为,故。于是设直线为,由得
所以:,
又
即:
由韦达定理得:
解得或(舍去)
经检验符合条件,故直线的方程为。
22.解:(Ⅰ)
(Ⅱ)由(Ⅰ)知。因为(当时取等号)。又
(Ⅲ),构造函数,则上式等价于证成立,所以。又令,则当时成立,即得在上单调递减,于是成立,即成立,故成立。所以,由此知单调递减,所以,即,所以
版权所有:高考资源网(www.)
酒精含量
频率
组距
0.02
0.015
0.01
0.005
0
20
30
40
50
60
70
80
90
100
(mg/100ml)
同课章节目录
