第13章立体几何初步 基础巩固测试-【新教材】2020-2021学年苏教版(2019)高中数学必修第二册(Word含解析)
文档属性
| 名称 | 第13章立体几何初步 基础巩固测试-【新教材】2020-2021学年苏教版(2019)高中数学必修第二册(Word含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-15 22:27:52 | ||
图片预览




文档简介
苏教版第13章立体几何初步基础巩固测试卷
一、单选题
1.下列说法不正确的是( )
A.三棱锥是四面体 B.三棱台是五面体
C.正方体是四棱柱 D.四棱柱是长方体
2.下列说法正确的是( )
A.三点确定一个平面
B.一条直线和一个点确定一个平面
C.梯形一定是平面图形
D.过平面外一点只有一条直线与该平面平行
3.如图,长方体被两平面分成三部分,其中,则这三个几何体中是棱柱的个数为( )
A.0 B.1 C.2 D.3
4.如图所示,是水平放置的的直观图,轴,轴,,,则中,( )
A. B. C. D.
5.若一个圆锥的母线长为4,且其侧面积为其轴截面面积的4倍,则该圆锥的高为( )
A.π B. C. D.
6.攒尖是古代中国建筑中屋顶的一种结构形式,常见的有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑.某园林建筑为六角攒尖,如图所示,它主要部分的轮廓可近似看作一个正六棱锥.设这个正六棱锥的侧面等腰三角形的顶角为,则底面内切圆半径与侧棱长的比为( )
A. B. C. D.
7.已知?是不重合的直线,?是不重合的平面,则下列命题正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
8.在正方体中,为的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
二、多选题
9.下列说法不正确的是( )
A.有两个面相互平行,其余各面都是平行四边形的几何体是棱柱
B.如果有一个几何体的三视图都相同,则该几何体一定是球
C.底面是等边三角形.侧面都是等腰三角形的三棱锥是正三棱锥
D.正四面体的所有棱都相等
10.已知直线a,b和平面,且,,则a与b的关系可以为( )
A.平行 B.相交 C.异面 D.垂直
11.以长为8 cm,宽为6 cm的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( )
A.64π cm2 B.36π cm2
C.54π cm2 D.48π cm2
12.设a,b是两条不重合的直线,,是两个不同的平面.下列四个命题中,正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
三、填空题
13.长方体中,,,,则三棱锥的体积为___________.
14.某圆台下底半径为2,上底半径为1,母线长为2,则该圆台的表面积为________.
15.如图,点P,Q,R,S分别在正方体的四条棱上,且是所在棱的中点,则直线PQ与RS是平行直线的图是________(填序号).
16.已知,是两条不同的直线,,是两个不同平面,则以下命题不成立的是__
(1)若,,,则
(2)若,,则
(3)若,,则
(4)若,,,则
四、解答题
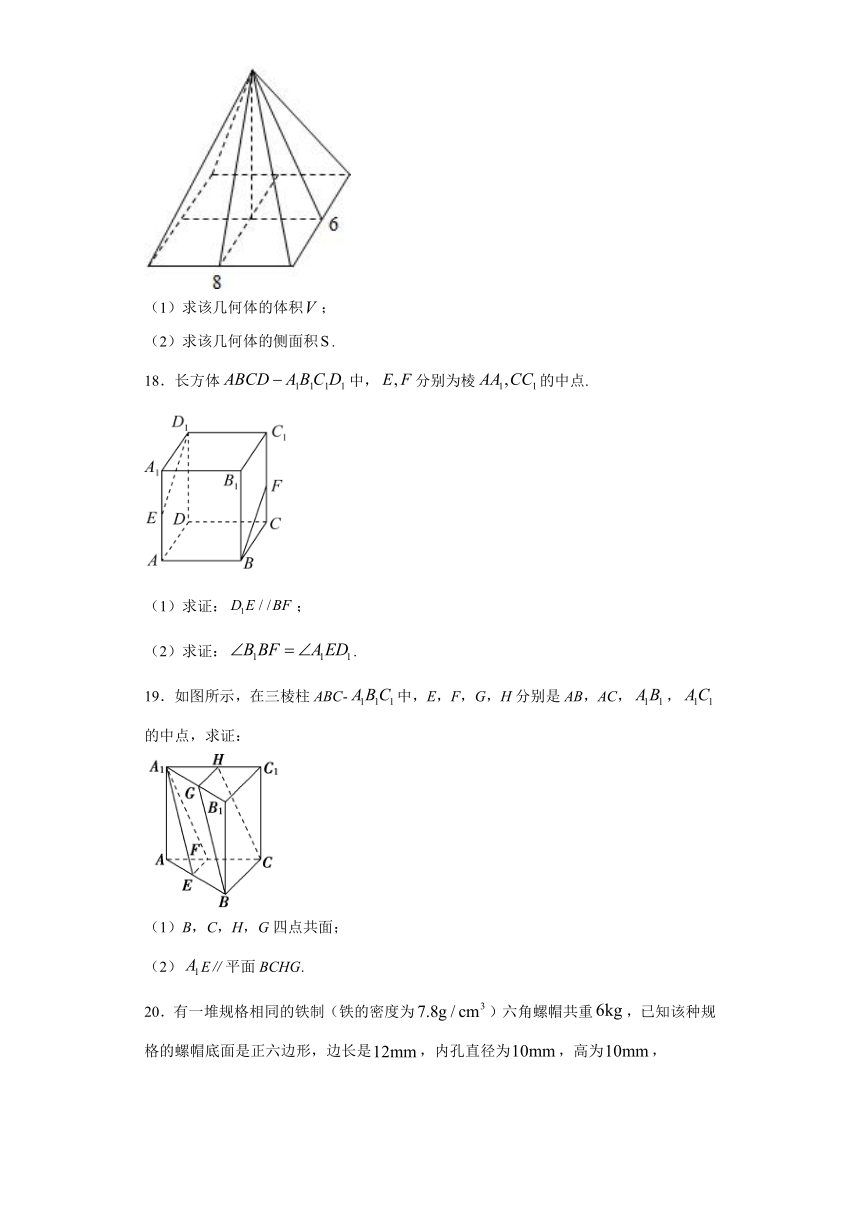
17.已知某几何体的直观图如图所示,其中底面为长为8,宽为6的长方形,顶点在底面投影为底面中心,高为4.
(1)求该几何体的体积;
(2)求该几何体的侧面积.
18.长方体中,分别为棱的中点.
(1)求证:;
(2)求证:.
19.如图所示,在三棱柱ABC?中,E,F,G,H分别是AB,AC,,的中点,求证:
(1)B,C,H,G四点共面;
(2)E∥平面BCHG.
20.有一堆规格相同的铁制(铁的密度为)六角螺帽共重,已知该种规格的螺帽底面是正六边形,边长是,内孔直径为,高为,
(1)求一个六角螺帽的体积;(精确到)
(2)问这堆六角螺帽大约有多少个?
(参考数据:)
21.如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,,侧面PAB底面,,
(1)求证:平面
(2)过AC的平面交PD于点M,若,求三棱锥的体积.
22.如图所示的几何体由等高的个圆柱和个圆柱拼接而成,点为弧的中点,且四点共面
(1)证明:平面
(2)若四边形为正方形,且四面体的体积为,求线段的长.
参考答案
1.D
【分析】
利用棱柱、棱锥、棱台的定义,判断选项即可.
【详解】
解:根据棱柱、棱锥、棱台的定义,选项A、B、C正确;
对选项D:只有底面是矩形的直四棱柱才是长方体,所以四棱柱是长方体不正确;
故选:D.
2.C
【分析】
由平面的基本性质,根据点、线、面的位置关系判断各选项的正误即可.
【详解】
A:不在一条直线上的三点确定一个平面,三点在一条直线上时不能确定平面,不正确;
B:点在直线上时,不能确定平面,不正确;
C:梯形有两条边平行,两条平行线确定一个平面,梯形的两腰也在平面内,正确;
D:过平面外一点与平面平行的平面内,过该点的直线都符合条件,不正确.
故选:C.
3.D
【分析】
根据棱柱的定义判断即可.
【详解】
长方体被两平面分成三部分,其中,
其中两个三棱柱,底面是直角三角形;
另一个是底面为6边形的直棱柱,
所以这三个几何体中是棱柱的个数为:3.
故选:D.
4.B
【分析】
根据斜二测画法原则,由直观图判断原图中的长度,再利用勾股定理计算.
【详解】
在直观图中,,,
由斜二侧画法知,在中,,,且;
所以.
故选:B.
5.A
【分析】
设圆锥的底面圆半径为r,高为h,由题意可得4πr=4rh,从而可得h=π
【详解】
设圆锥的底面圆半径为r,高为h;
由圆锥的母线长为4,
所以圆锥的侧面积为πr?4=4πr;
又圆锥的轴截面面积为?2r?h=rh,
所以4πr=4rh,
解得h=π;
所以该圆锥的高为π.
故选:A.
6.B
【分析】
根据等腰三角形的边角关系,用和表示出的一半,从而得出底面内切圆半径与侧棱长的比.
【详解】
设为正六棱锥底面内切圆的圆心,
连接,,如图所示:
由题意可知,,
,,
,
设内切圆半径为,则,,
底面内切圆的半径与侧棱的比为.
故选:B
7.D
【分析】
由空间中的线线、线面、面面关系逐个分析判断即可
【详解】
若,,则与可能平行也可能异面,故为假命题;
若,,则与也可能相交,故为假命题;
若,,则可能在平面上,故为假命题;
在中,此命题正确.因为垂直于同一直线的两个平面互相平行;
故选:D.
8.A
【分析】
连结,,利用,得到即为异面直线与所成的角,在中,由余弦定理求解即可.
【详解】
连结,,
在正方体中,易得,
所以或其补角为异面直线与所成的角,
设正方体的棱长为2,则,,,
在中,由余弦定理可得,
.
所以异面直线与所成角的余弦值为.
故选:A.
9.ABC
【分析】
根据棱柱的概念、正方体的三视图、正棱锥的概念以及正面体的概念可得选项.
【详解】
对于A:由棱柱的概念“有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都是互相平行的几何体叫棱柱”知A不正确;
对于B:正方体的三视图也都相同,故B不正确;
对于C:侧面为等腰三角形,但不一定侧棱就是两腰,故C不正确;
对于D:正四面体的各条棱都相等,故D正确,
故选:ABC.
10.BCD
【分析】
根据是否共面,讨论,时之间的位置关系即可.
【详解】
当共面,若,则且相交;当不共面,若,则且不相交,即异面垂直关系;
故选:BCD
11.AB
【分析】
分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,根据圆的面积公式即可求解.
【详解】
分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,
即可得到两种不同大小的圆柱,其底面面积分别为64π cm2,36π cm2.
故选:AB
12.BCD
【分析】
根据空间中线面的关系,逐一分析选项,即可得答案.
【详解】
对于A:若,,则可平行,可相交,也可异面,故A错误;
对于B:若,,则,故B正确;
对于C:若,,则,故C正确;
对于D:,,则,故D正确.
故选:BCD
13.
【分析】
根据长方体的结构特征,得到即为三棱锥的高,再由棱锥的体积公式,即可得出结果.
【详解】
因为长方体中,侧棱和底面垂直,
因此即为三棱锥的高,
所以三棱锥的体积为.
故答案为:.
14.
【分析】
由圆台的表面积公式计算.
【详解】
由题意该圆台的表面积为.
故答案为:.
15.①②
【分析】
根据正方体的结构特征,以及两直线的位置关系的判定方法,即可求解.
【详解】
根据正方体的结构特征,可得①②中RS与PQ均是平行直线,④中RS和PQ是相交直线,③中RS和PQ是是异面直线.
故答案为:①②.
16.(1)(2)(4)
【分析】
由线线、线面、面面的位置关系,判断线、面有关命题的真假即可.
【详解】
由,是两条不同的直线,,是两个不同平面,知:
在(1)中,若,,,则与平行或异面,错误;
在(2)中,若,,则与相交、平行或,错误;
在(3)中,若,,则由面面垂直的判定定理得,正确;
在(4)中,若,,,则与相交或平行,错误.
故答案为:(1)(2)(4).
17.(1)64;(2).
【分析】
(1)利用棱锥的体积公式直接计算;
(2)先利用勾股定理求得各侧面上的斜高,再求各侧面面积之和即得棱锥的侧面积.
【详解】
(1)几何体的体积为
.
(2)正侧面及相对侧面底边上的高为:
.
左、右侧面的底边上的高为:
.
故几何体的侧面面积为:
.
【点睛】
本题考查棱锥的体积和侧面积的求法,求侧面积关键在于侧面上的斜高的计算,关键要掌握顶点在底面上的投影是底面中心的意义,知道高垂直于底面内的直线,高于底面内的边心距和侧面的斜高构成直角三角形.
18.(1)证明见解析;(2)证明见解析.
【分析】
(1)先证明四边形为平行四边形,可得,再证明四边形为平行四边形,得,从而得;(2)根据等角定理证明即可.
【详解】
证明:(1)如图,取的中点,连接.
在矩形中,易得,
因为,,所以,
所以四边形为平行四边形,所以.
在矩形中,易得,.
所以四边形为平行四边形,
所以,所以.
(2)因为,,
又与的对应边方向相同,
所以.
19.(1)证明见详解;(2)证明见详解;
【分析】
(1)由中点知为中位线,即有,结合三棱柱的性质可证,即四点共面.
(2)由三棱柱的性质以及中点性质有平行且相等,即有,结合线面平行的判定即可证面.
【详解】
(1)∵G,H分别是,的中点,
∴,而,
∴,即B,C,H,G四点共面.
(2)∵E,G分别是AB,的中点,
∴平行且相等,所以四边形为平行四边形,即,又面,面,
∴面,
20.(1);(2)261个.
【分析】
(1)利用六棱柱的体积减去圆柱的体积即得解;
(2)计算即得解.
【详解】
(1)由题得
(2)这堆螺帽的个数为:(个)
答:每个螺帽的体积为,共有261个螺帽.
【点睛】
本题主要考查空间几何体的体积的计算,意在考查学生对这些知识的理解掌握水平.
21.(1)证明见解析;(2)
【分析】
(1)由菱形的性质有,勾股定理知,结合面面垂直的推论可得,根据线面垂直的判定证垂直即可;(2)由面即可计算,结合已知条件可求三棱锥的体积;
【详解】
(1)由题意知:底面ABCD是菱形,且
∴,又在△中,,即,
∴,又面PAB面,面PAB 面,面PAB,
∴面,而面,有:,,
∴平面;
(2)由(1)知:面,有,
而,且,
∴
【点睛】
本题考查了应用几何图形的性质,及线面垂直的判定证明垂直,根据已知体积关系结合三棱锥的体积公式求三棱锥的体积.
22.(1)证明见解析;(2).
【分析】
(1)取弧的中点,连结,,根据线线垂直证明线面垂直;
(2)设,根据体积为,列方程,可求的值,再由勾股定理求得的长.
【详解】
(1)取弧的中点,连结,,
则,
所以,
因为,
所以四边形为平行四边形,,
又因为平面,
所以,
所以平面.
(2)设,因为四边形ADEF为正方形,
则,解得:,
.
【点睛】
求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.
一、单选题
1.下列说法不正确的是( )
A.三棱锥是四面体 B.三棱台是五面体
C.正方体是四棱柱 D.四棱柱是长方体
2.下列说法正确的是( )
A.三点确定一个平面
B.一条直线和一个点确定一个平面
C.梯形一定是平面图形
D.过平面外一点只有一条直线与该平面平行
3.如图,长方体被两平面分成三部分,其中,则这三个几何体中是棱柱的个数为( )
A.0 B.1 C.2 D.3
4.如图所示,是水平放置的的直观图,轴,轴,,,则中,( )
A. B. C. D.
5.若一个圆锥的母线长为4,且其侧面积为其轴截面面积的4倍,则该圆锥的高为( )
A.π B. C. D.
6.攒尖是古代中国建筑中屋顶的一种结构形式,常见的有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑.某园林建筑为六角攒尖,如图所示,它主要部分的轮廓可近似看作一个正六棱锥.设这个正六棱锥的侧面等腰三角形的顶角为,则底面内切圆半径与侧棱长的比为( )
A. B. C. D.
7.已知?是不重合的直线,?是不重合的平面,则下列命题正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
8.在正方体中,为的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
二、多选题
9.下列说法不正确的是( )
A.有两个面相互平行,其余各面都是平行四边形的几何体是棱柱
B.如果有一个几何体的三视图都相同,则该几何体一定是球
C.底面是等边三角形.侧面都是等腰三角形的三棱锥是正三棱锥
D.正四面体的所有棱都相等
10.已知直线a,b和平面,且,,则a与b的关系可以为( )
A.平行 B.相交 C.异面 D.垂直
11.以长为8 cm,宽为6 cm的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( )
A.64π cm2 B.36π cm2
C.54π cm2 D.48π cm2
12.设a,b是两条不重合的直线,,是两个不同的平面.下列四个命题中,正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
三、填空题
13.长方体中,,,,则三棱锥的体积为___________.
14.某圆台下底半径为2,上底半径为1,母线长为2,则该圆台的表面积为________.
15.如图,点P,Q,R,S分别在正方体的四条棱上,且是所在棱的中点,则直线PQ与RS是平行直线的图是________(填序号).
16.已知,是两条不同的直线,,是两个不同平面,则以下命题不成立的是__
(1)若,,,则
(2)若,,则
(3)若,,则
(4)若,,,则
四、解答题
17.已知某几何体的直观图如图所示,其中底面为长为8,宽为6的长方形,顶点在底面投影为底面中心,高为4.
(1)求该几何体的体积;
(2)求该几何体的侧面积.
18.长方体中,分别为棱的中点.
(1)求证:;
(2)求证:.
19.如图所示,在三棱柱ABC?中,E,F,G,H分别是AB,AC,,的中点,求证:
(1)B,C,H,G四点共面;
(2)E∥平面BCHG.
20.有一堆规格相同的铁制(铁的密度为)六角螺帽共重,已知该种规格的螺帽底面是正六边形,边长是,内孔直径为,高为,
(1)求一个六角螺帽的体积;(精确到)
(2)问这堆六角螺帽大约有多少个?
(参考数据:)
21.如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,,侧面PAB底面,,
(1)求证:平面
(2)过AC的平面交PD于点M,若,求三棱锥的体积.
22.如图所示的几何体由等高的个圆柱和个圆柱拼接而成,点为弧的中点,且四点共面
(1)证明:平面
(2)若四边形为正方形,且四面体的体积为,求线段的长.
参考答案
1.D
【分析】
利用棱柱、棱锥、棱台的定义,判断选项即可.
【详解】
解:根据棱柱、棱锥、棱台的定义,选项A、B、C正确;
对选项D:只有底面是矩形的直四棱柱才是长方体,所以四棱柱是长方体不正确;
故选:D.
2.C
【分析】
由平面的基本性质,根据点、线、面的位置关系判断各选项的正误即可.
【详解】
A:不在一条直线上的三点确定一个平面,三点在一条直线上时不能确定平面,不正确;
B:点在直线上时,不能确定平面,不正确;
C:梯形有两条边平行,两条平行线确定一个平面,梯形的两腰也在平面内,正确;
D:过平面外一点与平面平行的平面内,过该点的直线都符合条件,不正确.
故选:C.
3.D
【分析】
根据棱柱的定义判断即可.
【详解】
长方体被两平面分成三部分,其中,
其中两个三棱柱,底面是直角三角形;
另一个是底面为6边形的直棱柱,
所以这三个几何体中是棱柱的个数为:3.
故选:D.
4.B
【分析】
根据斜二测画法原则,由直观图判断原图中的长度,再利用勾股定理计算.
【详解】
在直观图中,,,
由斜二侧画法知,在中,,,且;
所以.
故选:B.
5.A
【分析】
设圆锥的底面圆半径为r,高为h,由题意可得4πr=4rh,从而可得h=π
【详解】
设圆锥的底面圆半径为r,高为h;
由圆锥的母线长为4,
所以圆锥的侧面积为πr?4=4πr;
又圆锥的轴截面面积为?2r?h=rh,
所以4πr=4rh,
解得h=π;
所以该圆锥的高为π.
故选:A.
6.B
【分析】
根据等腰三角形的边角关系,用和表示出的一半,从而得出底面内切圆半径与侧棱长的比.
【详解】
设为正六棱锥底面内切圆的圆心,
连接,,如图所示:
由题意可知,,
,,
,
设内切圆半径为,则,,
底面内切圆的半径与侧棱的比为.
故选:B
7.D
【分析】
由空间中的线线、线面、面面关系逐个分析判断即可
【详解】
若,,则与可能平行也可能异面,故为假命题;
若,,则与也可能相交,故为假命题;
若,,则可能在平面上,故为假命题;
在中,此命题正确.因为垂直于同一直线的两个平面互相平行;
故选:D.
8.A
【分析】
连结,,利用,得到即为异面直线与所成的角,在中,由余弦定理求解即可.
【详解】
连结,,
在正方体中,易得,
所以或其补角为异面直线与所成的角,
设正方体的棱长为2,则,,,
在中,由余弦定理可得,
.
所以异面直线与所成角的余弦值为.
故选:A.
9.ABC
【分析】
根据棱柱的概念、正方体的三视图、正棱锥的概念以及正面体的概念可得选项.
【详解】
对于A:由棱柱的概念“有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都是互相平行的几何体叫棱柱”知A不正确;
对于B:正方体的三视图也都相同,故B不正确;
对于C:侧面为等腰三角形,但不一定侧棱就是两腰,故C不正确;
对于D:正四面体的各条棱都相等,故D正确,
故选:ABC.
10.BCD
【分析】
根据是否共面,讨论,时之间的位置关系即可.
【详解】
当共面,若,则且相交;当不共面,若,则且不相交,即异面垂直关系;
故选:BCD
11.AB
【分析】
分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,根据圆的面积公式即可求解.
【详解】
分别以长为8 cm,宽为6 cm的边所在的直线为旋转轴,
即可得到两种不同大小的圆柱,其底面面积分别为64π cm2,36π cm2.
故选:AB
12.BCD
【分析】
根据空间中线面的关系,逐一分析选项,即可得答案.
【详解】
对于A:若,,则可平行,可相交,也可异面,故A错误;
对于B:若,,则,故B正确;
对于C:若,,则,故C正确;
对于D:,,则,故D正确.
故选:BCD
13.
【分析】
根据长方体的结构特征,得到即为三棱锥的高,再由棱锥的体积公式,即可得出结果.
【详解】
因为长方体中,侧棱和底面垂直,
因此即为三棱锥的高,
所以三棱锥的体积为.
故答案为:.
14.
【分析】
由圆台的表面积公式计算.
【详解】
由题意该圆台的表面积为.
故答案为:.
15.①②
【分析】
根据正方体的结构特征,以及两直线的位置关系的判定方法,即可求解.
【详解】
根据正方体的结构特征,可得①②中RS与PQ均是平行直线,④中RS和PQ是相交直线,③中RS和PQ是是异面直线.
故答案为:①②.
16.(1)(2)(4)
【分析】
由线线、线面、面面的位置关系,判断线、面有关命题的真假即可.
【详解】
由,是两条不同的直线,,是两个不同平面,知:
在(1)中,若,,,则与平行或异面,错误;
在(2)中,若,,则与相交、平行或,错误;
在(3)中,若,,则由面面垂直的判定定理得,正确;
在(4)中,若,,,则与相交或平行,错误.
故答案为:(1)(2)(4).
17.(1)64;(2).
【分析】
(1)利用棱锥的体积公式直接计算;
(2)先利用勾股定理求得各侧面上的斜高,再求各侧面面积之和即得棱锥的侧面积.
【详解】
(1)几何体的体积为
.
(2)正侧面及相对侧面底边上的高为:
.
左、右侧面的底边上的高为:
.
故几何体的侧面面积为:
.
【点睛】
本题考查棱锥的体积和侧面积的求法,求侧面积关键在于侧面上的斜高的计算,关键要掌握顶点在底面上的投影是底面中心的意义,知道高垂直于底面内的直线,高于底面内的边心距和侧面的斜高构成直角三角形.
18.(1)证明见解析;(2)证明见解析.
【分析】
(1)先证明四边形为平行四边形,可得,再证明四边形为平行四边形,得,从而得;(2)根据等角定理证明即可.
【详解】
证明:(1)如图,取的中点,连接.
在矩形中,易得,
因为,,所以,
所以四边形为平行四边形,所以.
在矩形中,易得,.
所以四边形为平行四边形,
所以,所以.
(2)因为,,
又与的对应边方向相同,
所以.
19.(1)证明见详解;(2)证明见详解;
【分析】
(1)由中点知为中位线,即有,结合三棱柱的性质可证,即四点共面.
(2)由三棱柱的性质以及中点性质有平行且相等,即有,结合线面平行的判定即可证面.
【详解】
(1)∵G,H分别是,的中点,
∴,而,
∴,即B,C,H,G四点共面.
(2)∵E,G分别是AB,的中点,
∴平行且相等,所以四边形为平行四边形,即,又面,面,
∴面,
20.(1);(2)261个.
【分析】
(1)利用六棱柱的体积减去圆柱的体积即得解;
(2)计算即得解.
【详解】
(1)由题得
(2)这堆螺帽的个数为:(个)
答:每个螺帽的体积为,共有261个螺帽.
【点睛】
本题主要考查空间几何体的体积的计算,意在考查学生对这些知识的理解掌握水平.
21.(1)证明见解析;(2)
【分析】
(1)由菱形的性质有,勾股定理知,结合面面垂直的推论可得,根据线面垂直的判定证垂直即可;(2)由面即可计算,结合已知条件可求三棱锥的体积;
【详解】
(1)由题意知:底面ABCD是菱形,且
∴,又在△中,,即,
∴,又面PAB面,面PAB 面,面PAB,
∴面,而面,有:,,
∴平面;
(2)由(1)知:面,有,
而,且,
∴
【点睛】
本题考查了应用几何图形的性质,及线面垂直的判定证明垂直,根据已知体积关系结合三棱锥的体积公式求三棱锥的体积.
22.(1)证明见解析;(2).
【分析】
(1)取弧的中点,连结,,根据线线垂直证明线面垂直;
(2)设,根据体积为,列方程,可求的值,再由勾股定理求得的长.
【详解】
(1)取弧的中点,连结,,
则,
所以,
因为,
所以四边形为平行四边形,,
又因为平面,
所以,
所以平面.
(2)设,因为四边形ADEF为正方形,
则,解得:,
.
【点睛】
求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
